車載穩定隔振平臺的慣性參數辨識方法研究

田體先 韓 意 馬玉浩 魯吉林 賴 震

（1.武漢科技大學，武漢 430081；2.陸軍裝備部裝備項目管理中心，北京 100007； 3.陸軍裝備部駐北京地區軍事代表局駐臨汾地區軍事代表室，侯馬 043000）

特種車輛被應用于各種復雜場景，如戰場環境下的全地形救護車。救護車輛行駛過程中會受到來自地形和車速變化的影響，且外部加速度的擾動隨機性較強，對車輛的沖擊較大。振動和沖擊會對傷員造成二次傷害，有必要采取措施隔離和緩沖其在動態環境中所受到的振動[1]。因此，根據醫療救護隔振平臺的使用要求進行相應的隔振設計具有重要意義[2]。

車載隔振平臺的類型很多，按減振機構的控制方式一般可分為被動隔振平臺、半主動隔振平臺和主動隔振平臺。6自由度并聯機構作為主動隔振平臺，具有精度高、承載能力大的優點。例如：哈爾濱工業大學研制的基于Stewart機構的八作動器隔振平臺[3]，采用氣壓作動器的方式提供主動隔振能力，且阻尼器與彈簧并聯，提高了隔振平臺的穩定性和可靠性，增加了系統的剛度和承載能力[4]。

2 6自由度隔振平臺動力學

6自由度隔振平臺結構示意圖，如圖1所示。它由1個上平臺、1個下平臺以及6個相互獨立的電動缸組成。6個支腿通過虎克鉸與上下平臺相連[5]。該機構具備空間6個自由度的運動能力，定義上平臺重心Oa、下平臺重心Ob，建立動坐標系Oaxayaza和固定坐標系Obxbybzb。上平臺鉸點中心和下平臺鉸點中心分別用ai和bi(i=1,…,6)表示。并聯機構的空間位姿采用廣義坐標p=[c,β]來表示，其中平移表示為c=[x,y,z]T，轉動姿態采用歐拉角表示β=[φ,θ,ψ]T，并按照Z-Y-X的順序實現轉動。

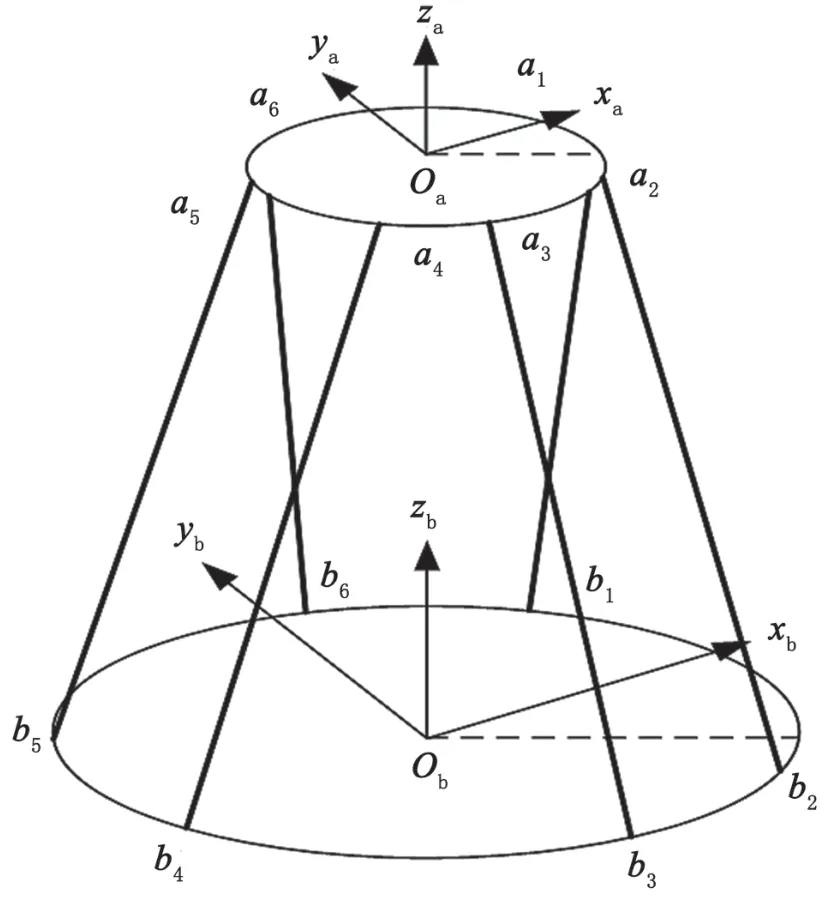
圖1 6自由度隔振平臺結構

2.1 慣性參數辨識模型

并聯平臺的動力學方程表述為：

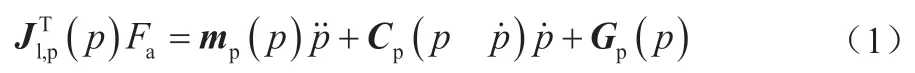
式中：mp(p)為上平臺質量矩陣；Cp(p p˙)為哥式力/向心力系數矩陣；Gp(p)為重力項矩陣；J1,p(p)為并聯平臺雅可比矩陣；支腿力Fa為支腿驅動力。

在電動6自由度隔振平臺中，支腿力由電動缸來提供。對電動缸進行動力學分析，建立以電機轉矩為輸入、支腿出力為輸出的傳遞函數模型，如圖2所示。

圖2 支腿動力學傳遞函數框圖

2.2 慣性參數辨識方法

當并聯平臺以正弦信號運動時，分析驅動力信號。由動力學方程式（1）可知，驅動力可分解為慣性力、科氏力、向心力、阻尼力和重力。其中，慣性力和阻尼力為與位姿信號頻率相同的基頻分量，科氏力和向心力為高頻分量，重力項為常量。因此，可分離慣性力中的基頻分量，從而辨識慣性參數。

采集信號時，將系統激勵力改寫為傅里葉形式，并提取其中的基頻分量構建辨識方程，為：

式中：Fs,c為激勵力信號的基頻分量系數矩陣。

將6次的激勵數據按順序排列，構成辨識方程為：

式中：W為速度與加速度基頻分量矩陣；H為力信號基頻分量矩陣。

對位姿信號正弦幅值分量S和力信號基頻分量H的計算采用最小二乘法，對式（3）進行求解，即可完成慣性參數的辨識。

3 慣性參數辨識仿真研究

實驗采用Adams和Matlab聯合仿真。在Adams中搭建好模型并設置相關參數，然后生成聯合仿真Adams_sub模塊。在Matlab中建立并聯機構上平臺參考軌跡模塊、位移反解模塊以及增益模塊，仿真結構模型如圖3所示。

圖3 仿真模型

圖3中：上平臺參考軌跡模塊負責對并聯平臺6個自由度產生激勵；反解模塊將上平臺的位姿反解為6個電缸的位移。仿真結束后，在Adams中提取電動缸的轉矩、位移等必要參數，帶入辨識算法中進行計算。辨識結果如表1所示。

表1 辨識結果

從表1可以看出，并聯平臺質量辨識誤差小于2%，轉動慣量辨識誤差小于7%，辨識值與實際值之間的誤差很小，證明采用轉矩辨識結果可靠、精確。

4 結語

本文推導了隔振平臺支腿動力學模型，建立了并聯機構隔振平臺的慣性參數辨識方程，提出了一種采用電機力矩信息構造的適用于電動6自由度隔振平臺的慣性參數辨識方法，并對提出的辨識方法進行了仿真研究。結果表明，該方法可準確獲得平臺慣性參數。