狹窄空間內復雜產品的裝配路徑規劃研究
熊 晶 段曉坤
(常州信息職業技術學院,常州 213164)
產品裝配路徑規劃是產品裝配工藝設計的重要內容之一。尤其是復雜產品,它的零部件數量多,結構復雜,內部空間緊湊。在狹窄空間內為待裝配的零部件計算出一條從裝配起點到裝配終點的無碰撞路徑,是虛擬裝配設計的難點之一。
基于幾何圖的路徑規劃算法,如柵格法[1],在路徑搜索之前,先對整個求解空間進行單元分割,并用分割單元對障礙空間和自由空間進行描述,再利用基于圖的搜索算法,如A*算法[2-3],在所構建的環境圖中搜索有效路徑,有利于獲得優化路徑解。但是,這種方式用于狹窄三維空間內的路徑求解時,分割單元的尺寸將直接決定狹窄空間內有效節點的數量、求解成功率與效率。分割單元尺寸過大時,有效節點過少,求解困難;分割尺寸過小時,則存在組合爆炸的情況。
快速擴展隨機樹(Rapid-exploring Random Tree,RRT)[4-5]是一種隨機采樣的路徑規劃算法,特點在于利用隨機性來處理C空間而無需對求解空間進行精確計算,因而廣泛應用于高維空間下的路徑規劃問題。但是,由于狹窄空間內產品裝配時受到的空間約束較大,使用RRT算法進行裝配路徑規劃時,隨機采樣點搜索到狹窄空間的概率低,路徑樹擴展的成功率和效率都有待提高。
針對以上問題,本文結合柵格法與RRT算法的優點改進RRT算法,以待擴展樹節點為中心,離散化局部空間,提出兩種運動策略及對應的評價指標,引導局部路徑的擴展。
本文主要創新點如下。
(1)提出一種局部位移和轉動空間的離散化方法,對待擴展樹節點附近的局部空間進行離散化設計,為路徑樹的擴展提供多種備選位姿,以提高路徑擴展的成功率與效率。
(2)根據裝配運動的難易程度,提出兩種運動策略及對應的評價指標,并依據評價指標對備選位姿進行選擇。
(3)基于上述局部空間離散化設計及兩種運動策略,提出一種改進的快速搜索隨機樹算法,用于狹窄空間內產品的虛擬裝配路徑求解。仿真實驗表明,此方法在求解成功率和效率方面具有有效性。
1 快速搜索隨機樹算法
RRT算法的基本原理是通過均勻和隨機地搜索狀態空間來遞增地擴展路徑樹,直到路徑樹的葉節點到達終點區域。
它的搜索路徑過程主要包括以下步驟。
(1)路徑樹初始化,即將路徑起點(裝配起點) (xstar,ystar,zstar)加入路徑樹中。
(2)路徑樹擴展。在自由空間內生成隨機采樣位姿點qrand,遍歷樹中節點,從而找到與qrand距離最近的節點qnear。從qnear出發,將路徑樹朝著qrand按照某種運動曲線或運動規律運動一定時間到達一個新的位姿點qnew。若該新位姿點qnew滿足碰撞約束要求,則將該點及其局部路徑加入路徑樹中,否則重新進行隨機采樣,直至路徑樹擴展成功。
(3)終止判斷。若新加入路徑樹的節點qnew與路徑終點(xgoal,ygoal,zgoal)之間的距離小于基礎值dth,則路徑搜索成功。
2 改進算法設計
在改進算法中,對待擴展樹節點附近的局部空間進行離散化設計,并為路徑樹的局部擴展提供兩種策略。每種策略提供多種備選位姿,以提高路徑樹局部擴展的成功率和效率。
2.1 局部空間離散化設計
產品零部件進行裝配時,裝配運動既包含移動又包含轉動,因此需要從移動和轉動兩個角度進行局部空間的離散化設計。
以當前路徑樹待擴展的樹節點為中心所構建的局部離散化空間,如圖1所示。該局部離散化空間由8個邊長為l的正方體單元組成。路徑樹擴展時,只能從圖1中正方體單元的頂點選擇新節點。產品移動運動可以選擇正方體單元的一條邊、一條面對角線或一條體對角線作為下一移動運動路線軌跡。由圖1可以看出,與當前待擴展的樹節點所相鄰的頂點共26個。
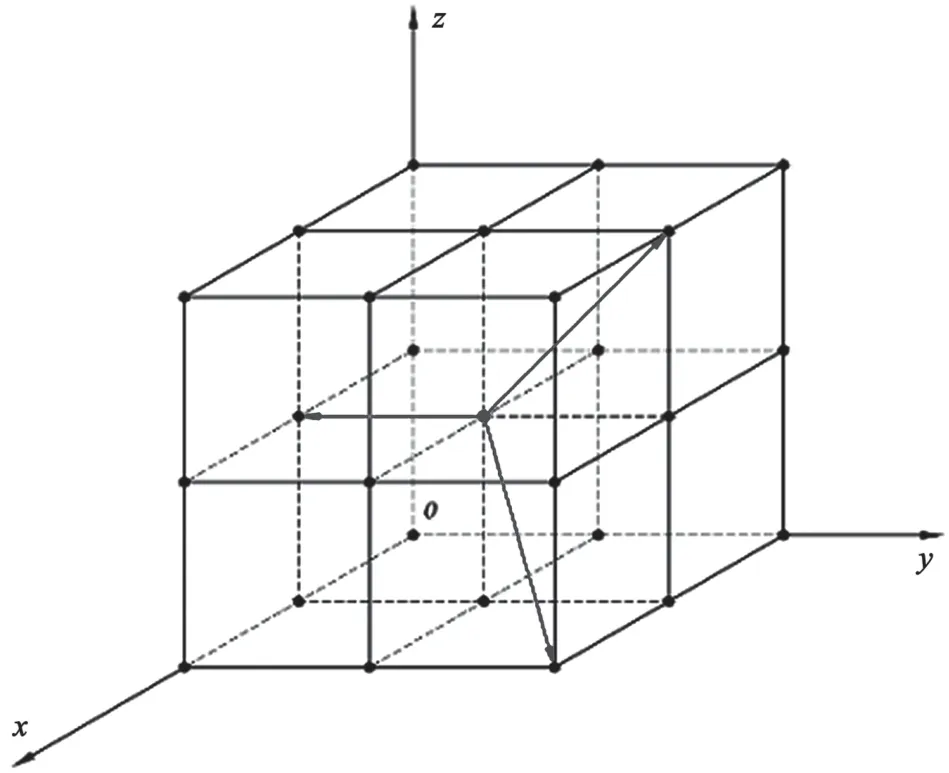
圖1 局部位移空間的離散化設計
這種空間的離散化設計與柵格法的不同之處在于,它的計算過程并非在路徑搜索開始之前完成,而是在路徑搜索過程中進行的,且無需對整個求解空間進行離散化,只需對待擴展路徑節點附近的局部空間進行離散化即可。隨著路徑樹的生長,待擴展樹節點與障礙物之間的距離發生變化,分割的單元尺寸l也可隨之變化。此時,可結合動態步長策略[6]動態地設計單元尺寸。
不同形狀的產品繞Z軸轉動的離散化設計,如圖2所示。相鄰姿勢之間的轉動角度間隔為αz,產品從當前姿勢到下一姿勢只能選擇逆時針轉動αz(記為正)或順時針轉動αz(記為負)。
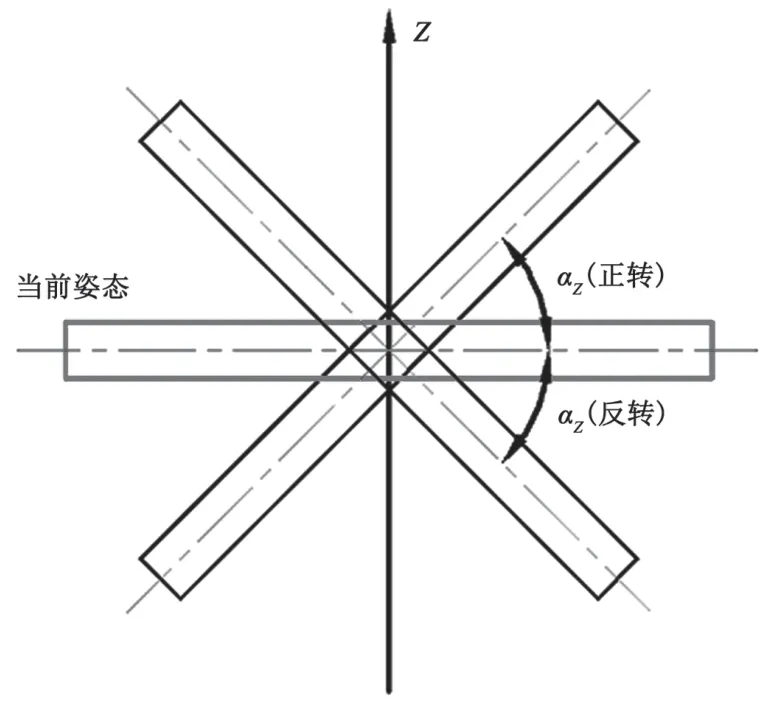
圖2 局部轉動空間的離散化設計(繞Z軸轉動)
假定繞軸X軸和Y軸轉動的離散化設計,相鄰位姿之間的轉動間隔分別為αX和αY。實際裝配運動中,產品相鄰姿勢之間的轉動可能是僅繞單軸轉動,也可能是繞兩軸轉動的復合運動,還可能是繞X軸、Y軸、Z軸3軸轉動的復合運動。它的轉動組合共24種,結合移動的26種情況,路徑樹的每一步擴展有674種選擇,包含僅平移、僅轉動和一邊移動一邊轉動。
為降低求解復雜性,本文只考慮相鄰位姿之間僅進行平移運動和繞單根軸轉動的情況。
2.2 裝配路徑規劃的運動策略與評價指標
為進一步提高求解速度,根據實際裝配時操作的難易程度,將路徑裝配分為僅平移(26種情況)和僅轉動(6種情況)兩種運動策略,其中將僅平移優先為最高級。進行裝配路徑規劃時,按照優先級的高低順序進行選擇。當高一級的運動策略中的幾種情況均不滿足要求時,再選擇低一級的運動策略。
同一運動策略中,有多種備選位姿,需要根據評價指標對各備選位姿進行評價,并根據評價指標進行排序和選擇備選位姿。若該備選位姿通過碰撞檢測,則將其加入路徑樹中,否則將其刪除,并更新備選位姿,再依據剩余備選位姿的排序重新選擇,直至有新節點加入路徑樹中。若某一運動策略中的所有備選位姿均不滿足要求,則選擇低一級的運動策略,并按該策略的評價指標對備選位姿進行評價、排序、選擇和檢測。
在僅平移運動策略中,從當前位姿至備選位姿均為僅平移運動,且平移距離均為分割單元正方體的邊長l,即從裝配起點經當前位姿至各備選位姿所產生的移動累計距離一致,但各備選位姿至終點位姿的實際距離不一致。以備選位姿至終點位姿的直線距離為僅平移運動策略的評價指標,備選位姿i評價指標為:
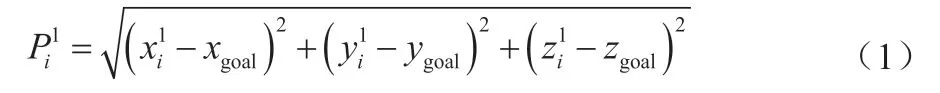
式中:i=1,2,…,26,表示備選位姿編號;(xi1,yi1,zi1)表示備選位姿坐標;(xgoal,ygoal,zgoal)表示終點坐標;Pi1越小,表明與終點越近,有利于加快路徑搜索進程。
在僅轉動策略中,從當前位姿至備選位姿均為僅轉動運動,轉動的方向只能是正轉或反轉,且位姿角度差只能是αX、αY或αZ。僅轉動策略中優先選擇正轉且轉動角度最小的備選位姿。若αX、αY或αZ角度值相等,則隨機選擇。
2.3 改進算法的流程設計
改進算法的流程如圖3所示。本算法基于“可拆即可裝”的思路[7],將裝配終點設置為路徑起點,將裝配起點設置為路徑終點,求解拆卸路徑。它只需將零部件移出產品包圍盒即可,無需關注拆卸終點零部件的姿態。獲得拆卸路徑后,對運動路徑進行重新排序,即可獲得裝配路徑。

圖3 改進算法流程圖
進行隨機采樣時,以一定的概率p選擇路徑終點為隨機采樣點。獲得隨機采樣點后,路徑樹首先朝隨機采樣點擴展。若路徑樹朝著隨機采樣點擴展失敗,表明當前樹節點在障礙物附近,則啟動局部空間離散化,對障礙物附近的局部路徑提供多種備選位姿。獲得與qrand距離最近的樹節點qnear后,隨即以qnear現在的位置和姿態為中心進行局部位移和局部轉動空間的離散化,獲得多個備選位姿。按照運動策略的優先級順序,先對僅平移策略中的備選位姿進行評價、排序、選擇及碰撞干涉檢驗,直至路徑樹局部擴展成功。若僅平移策略中的備選位姿均不滿足要求,則對僅轉動策略中的備選位姿進行評價、排序、選擇及碰撞干涉檢驗,直至路徑樹局部擴展成功。若僅轉動策略中的備選位姿仍不滿足要求,則重新進行隨機采樣點的選擇,并重復以上過程,直至有備選位姿加入路徑樹,完成一次擴展樹的過程。路徑樹多次擴展成功,直至擴展到拆卸路徑終點附近,拆卸路徑搜索過程結束。路徑節點重新排序后,返回從裝配起點至終點的路徑。
3 仿真驗證與結果分析
為驗證所提出方法的有效性,對引擎活塞桿帽裝配路徑進行規劃仿真實驗。裝配起點與終點如圖4所示,其中裝配終點附近約束強烈,是典型的狹窄空間下的裝配路徑規劃問題。
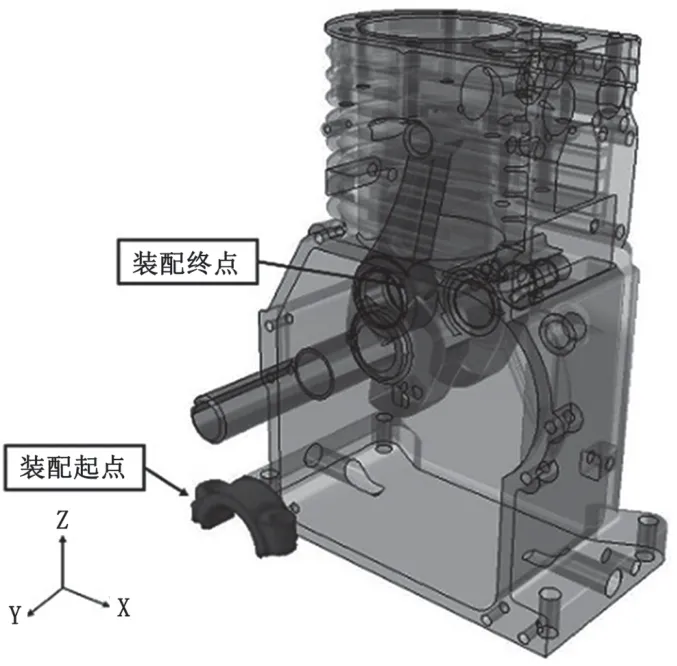
圖4 活塞桿帽裝配路徑規劃的起點與終點
將本文算法與RRT算法和Biased-RRT[8]算法比較后,可得所提方法適用于狹窄空間內復雜產品的裝配路徑規劃問題。在仿真實驗中,三維空間在OX、OY和OZ這3個方向上的范圍均為0~500 mm,其他仿真參數如表1所示。

表1 仿真參數設置表
3種算法在解決如圖4所示的裝配路徑問題時的表現如表2所示。由于RRT算法具有隨機性,故表2中成功率指的是算法重復執行100次時搜索成功次數與總次數的比值。搜索時,設定每次執行時最大允許迭代次數為100,在允許的迭代次數內返回裝配路徑即表示此次搜索成功,超過迭代次數還未返回路徑則表明路徑搜索失敗。

表2 算法表現對比表
從表2可知,改進算法找到路徑的成功率和效率最高。相比于RRT算法和Biased-RRT算法,本文提出的改進算法先朝向隨機采樣點擴展,若擴展不成功再進行局部離散化,為局部路徑的擴展提供了多種選擇。只要存在可擴展點,則該局部路徑即可擴展成功。這一策略有利于提高狹窄空間中路徑擴展的成功率和效率。
改進算法獲得的裝配路徑,如圖5所示。該裝配路徑是由所獲得的拆卸路徑各節點重新排序獲得,而拆卸路徑規劃過程中只要零件拆出產品包圍盒即可,無需保證拆出時的姿態與拆卸終點(裝配起點)的姿態一致,故圖5中裝配起點處的局部運動姿態有較大改變,而這一局部運動在開闊區域完成,認為是可接受的。
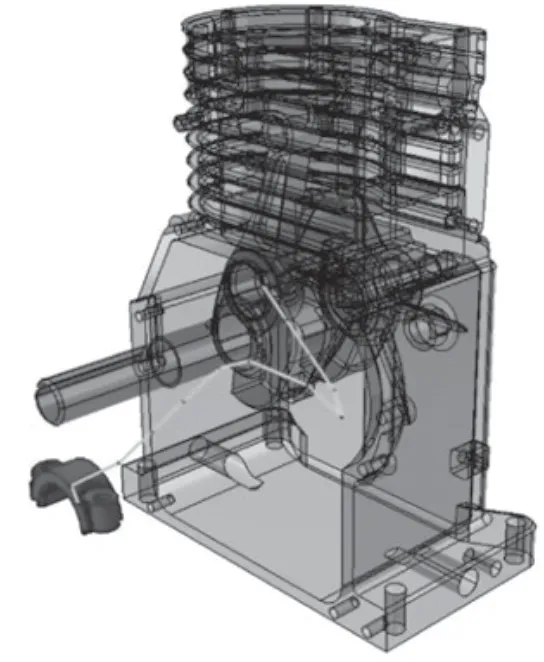
圖5 改進算法所生成的路徑
4 結語
針對狹窄空間中復雜產品裝配路徑規劃成功率和求解效率低的問題,提出一種改進的快速搜索隨機樹算法。此方法將路徑節點的局部空間離散化,提供多個備選位姿,提出兩種運動策略及對應的評價指標,提高了路徑擴展的成功率與效率。仿真實驗結果表明,此方法可有效解決狹窄空間中的裝配路徑規劃問題,并可提高求解成功率與效率。

