基于DADOS 的某大型組合式壓力機上橫梁輕量化設計
趙永剛, 凡曉波, 宋學官
(大連理工大學 機械工程學院, 遼寧 大連116024)
0 引言
壓力機是制造行業必不可少的重要裝備之一, 在航空、航天、汽車、輪船等領域廣泛應用,其中大型壓力機更是一個體現國家科技水平和綜合國力的重要標志。 上橫梁作為大型壓力機設備的主要承力構件之一, 設計者在進行設計時,往往按照較為保守的經驗進行設計,造成其質量過重,剛度冗余過多的問題。所以對上橫梁進行輕量化設計具有重要意義。
1 有限元分析
某大型壓力機的上橫梁結構如圖1 所示, 從圖中可以看出,該橫梁結構由四個分橫梁組合而成,各分橫梁所受豎直向上推力的合力相同。 由于各分橫梁結構相似,本文選取其中一個分橫梁作為研究對象進行輕量化設計,其他分橫梁設計方法相同。
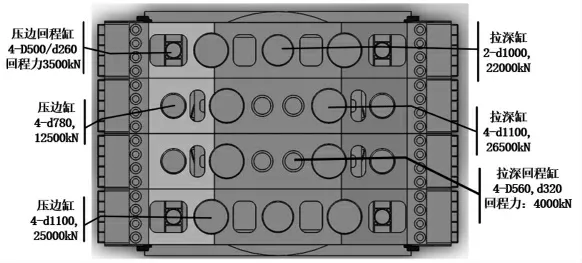
圖1 上橫梁結構及油缸分布圖
1.1 建立三維模型
分橫梁三維模型如圖2 所示, 主要由上蓋板、 側壁板、肋板和下底板組成。 考慮該設計是在原設計基礎上進行優化, 故提取了4 個可優化設計變量x1-x4, 如圖3 所示, 其中x1為肋板厚度,x2為壁板厚度,x3為上蓋板中線與下底板中線間距,x4為上蓋板厚度。 4 個設計變量的初始值及取值范圍如表1 所示。

圖2 橫梁結構三維模型

圖3 橫梁結構設計變量示意圖

表1 變量初始值及范圍
1.2 材料參數
該分橫梁材料為Q235-B,其相關參數如表2 所示。

表2 Q235- B 材料屬性
1.3 仿真分析
根據該分橫梁的結構特點,采用四面體網格類型,對整體及四分之一模型進行網格劃分。該橫梁工作時,主要載荷為1 個壓邊缸及2 個拉伸缸的豎直向上推力, 橫梁兩端采用固定約束,模型約束及載荷情況如圖4 所示。
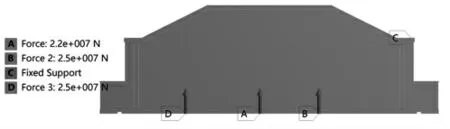
圖4 載荷及約束設置
經過有限元分析, 結構的整體模型及四分之一模型的變形云圖如圖5、圖6 所示,兩模型的變形峰值基本相同,為3.129mm。 為降低計算量,本文采用四分之一模型進行仿真分析。模型最大應力較小,約為140MPa,故在本設計中僅在優化結果中進行驗證。

圖5 整體結構變形云圖
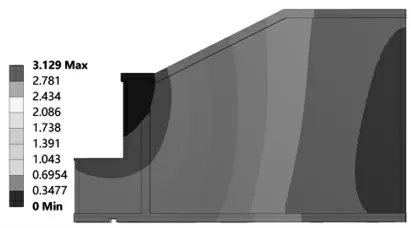
圖6 四分之一結構變形云圖
2 基于DADOS 平臺的優化分析
DADOS 平臺是由大連理工大學宋學官教授團隊開發的一款數據驅動的云端優化設計平臺 (網址:http://www.dados.com.cn/)。 該平臺提供了基于代理模型的優化設計全流程的各個模塊,每個模塊由多種算法構成,可滿足不同的設計需求。 基于代理模型的優化設計流程見圖7。

圖7 基于代理模型的優化設計流程
2.1 優化問題定義
在保證剛度和強度的前提下,通過優化橫梁尺寸及形狀參數,達到降低橫梁重量的目的,可定義優化問題為:

式中:x=[x1,x2,x3,x4],M(x)—橫梁質量;D(x)—橫梁結構最大變形;w—最大變形系數。
2.2 基于代理模型的優化分析
代理模型是指通過采樣點及試驗或仿真獲取的響應值建立輸入與輸出之間關系的數學模型,可表示為:

式中:Xtrain—采樣點;Ytrain—響應值;x—設計變量;y^—預測值。
當建立的代理模型精度滿足設計要求時, 設計者可用該模型替代試驗或仿真進行優化分析,達到降低成本、縮短設計周期的目的。
本文采用DADOS 平臺試驗設計模塊的LHS 采樣方法獲取60 個樣本點,以x1與x2為例,其空間分布見圖8。
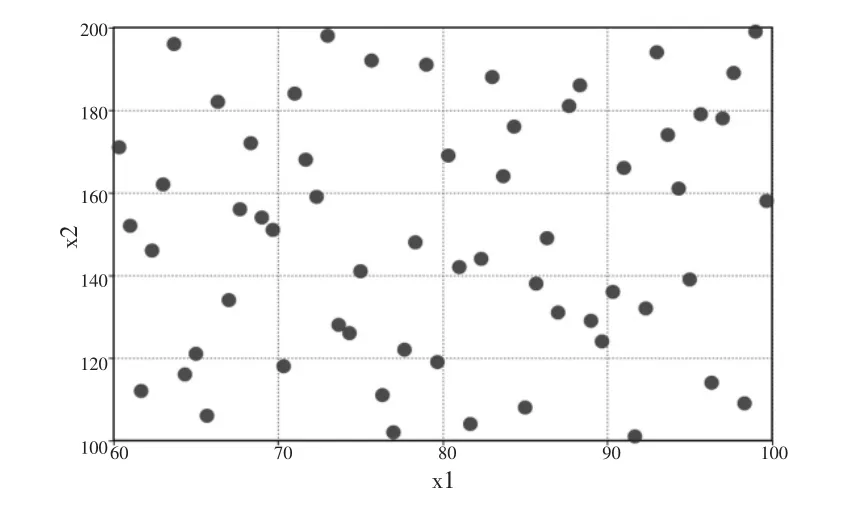
圖8 采樣點空間分布
采用代理模型模塊中徑向基函數(RBF),多項式響應面法(PRS),移動最小二乘法(MLS),支持向量機回歸(SVR),人工神經網絡(ANN)分別建立M(x)和D(x)的代理模型,并采用精度校驗模塊中的留一法[1]計算模型的決定系數R2,R2計算公式為:

式中:yi—采樣點xi的真實響應值; y^i—采樣點xi的預測值;m—采樣點的數量;yˉ為yi的均值。
R2的范圍為[0,1],R2越大,模型精度越高,模型擬合效果越好。 各模型的R2值如表3 所示。 選取模型精度最高的PRS 模型及MLS 模型分別建立M(x)和D(x)的代理模型。
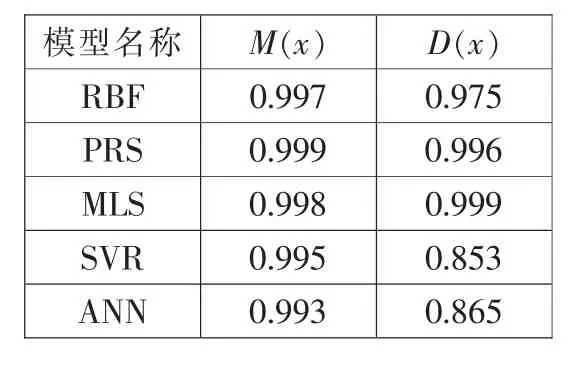
表3 各模型R2 值
PRS 模型是通過多項式方程來擬合輸入與輸出之間的關系,通過最小二乘法來求解多項式各項系數,從而構建代理模型[2]。 本文采用三階多項式模型,其具體公式為:
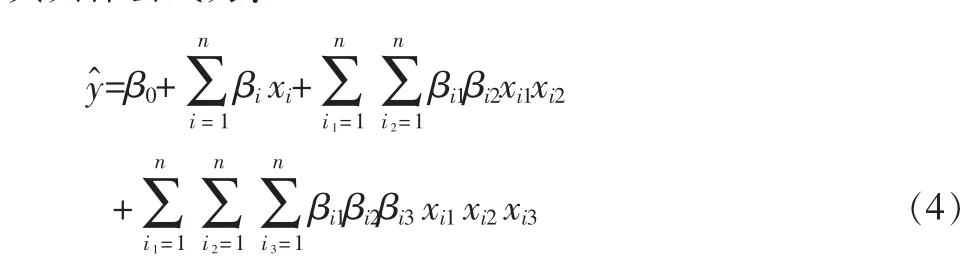
式中:β—多項式系數;n—變量數目。
MLS 模型是形成無網格方法逼近函數的方法之一,與傳統的最小二乘法的區別在于: 建立了由系數向量a(x)和基函數p(x)構成的擬合函數,引入了緊支概念,限制x 的影響區域[3]。 其公式為:
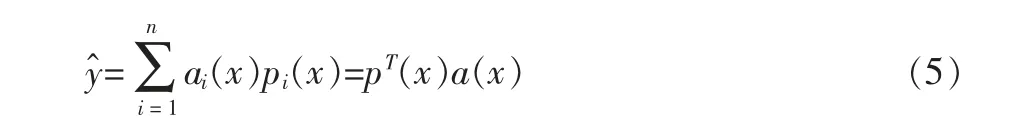
式中:p(x)=[p1(x),p2(x),…,pm(x)]T是一個m 階的多項式基函數,a(x)=[a1(x),a2(x),…,am(x)]是待求系數向量。 基函數的類型有以下幾種,見表4。

表4 MLS 基函數類型
2.3 優化分析
敏感性分析是研究模型中輸入變量在取值范圍內變動對輸出影響程度的方法, 影響程度的衡量標準被稱為敏感性系數,敏感性系數越大,該變量對模型輸出影響越大[4]。
本文采用DADOS 平臺敏感度分析模塊中的SOBOL[5]法對模型進行敏感性分析,各模型一階、全階敏感性值統計見圖9, 圖10 所示。 由圖可以看出各變量間的相互影響較弱, 變量x2,x3為影響質量及最大應力的主要因素,在優化設計中,應重點考慮。采用DADOS 平臺優化模塊的遺傳算法(GA),粒子群算法(PSO),模擬退火算法(SA)分別進行優化求解,結果見表5。

表5 優化結果

圖9 質量模型敏感性分析

圖10 最大變形模型敏感性分析
由優化結果可知,通過提高橫梁整體高度x3,減小壁板厚度x2的方式,可實現輕量化設計。 由于x1、x4對質量和變形的影響較小,在優化搜索過程中,隨機性較大,優化結果間誤差較大。
2.4 優化結果驗證
將優化結果進行仿真驗證, 預測值與仿真結果對比如表6 所示。由表中結果分析可得:該最大應力小于材料許用應力,滿足設計要;D(x)模型誤差約為0.35%,M(x)模型誤差約為0.18%, 預測值與仿真結果基本一致;優化前該分橫梁總質量為320092kg,優化后質量為304820kg,減重約4.77%。

表6 預測與仿真結果對比
3 結論
本文以某大型壓力機上橫梁為研究對象,采用有限元法,獲取模型最大變形及最大應力。應用基于代理模型的優化設計方法,建立了高精度的代理模型,較為快速的尋找到了較優解。通過仿真驗證,證明了優化結果的可行性及準確性,將該分橫梁減重約4.77%。 此外,本文建立了一套基于代理模型的輕量化設計流程, 可為相似結構的輕量化設計提供思路。

