單人跳躍荷載實驗及其特征研究

高延安,田新強，葉姝彤，王慧婷，徐 彤，鄒長軒，丁 怡

(淮陰工學院 建筑工程學院, 江蘇 淮安 223001)

隨著高強度、低阻尼比材料在大跨大尺度結構中的廣泛應用，人群活動引起結構的振動問題也越發顯著。而對人體激勵荷載的正確提取是工程設計與結構分析的基本前提。目前對結構的人致振動研究非常頻繁，如人行橋人致振動響應[1-2]、樓蓋的人致振動舒適性[3]、樓梯的人致振動[4]等，但對人的激勵荷載研究相對較少。關于人的荷載研究主要集中在步行荷載，如早期國外學者對雙足步行荷載進行了測試分析[5-6]，國內學者對其特征開展了進一步研究[7-9]。如圖 1所示為從我國期刊中篩選出445篇關于人致振動相關文章的研究主題分布關聯特征圖，可知目前對結構人致振動研究做的工作量最大，而對人的跳躍荷載研究相對較少，由于在公共場合如橋梁、體育場等結構中，人的跳躍活動更易引起結構的振動問題而受到普遍關注。Sim等[10]早期系統研究了人群跳躍荷載模型和相位差，并對荷載的時間特征、荷載形狀及其擬合分布統計特征進行了分析。國內陳雋等[11]較早開始對單人跳躍的荷載模型和參數取值進行了精細化研究，之后進一步對其動力特征[12]、功率譜特征[13]進行研究，并利用深度學習網絡模型[14]對其進行計算機自動生成實驗研究。為進一步獲得大樣本荷載特征，朱萍[15]對1218人次的跳躍實驗進行了測試獲得了人體跳躍荷載的頻率、動力放大系數等統計分布參數。雖然學者們目前對人體跳躍荷載進行了一系列系統研究，但主要考慮其應用較多，而對人體跳躍荷載本身的研究非常少，為進一步充實我國人體跳躍荷載統計特征，基于大量樣本條件對人體的寬頻帶跳躍激勵荷載進行了系統研究，分析了身高體重參數、荷載激勵頻率分布、荷載模型參數等統計特征，以期為土木工程結構的人致振動設計與控制提供荷載設計參考依據。

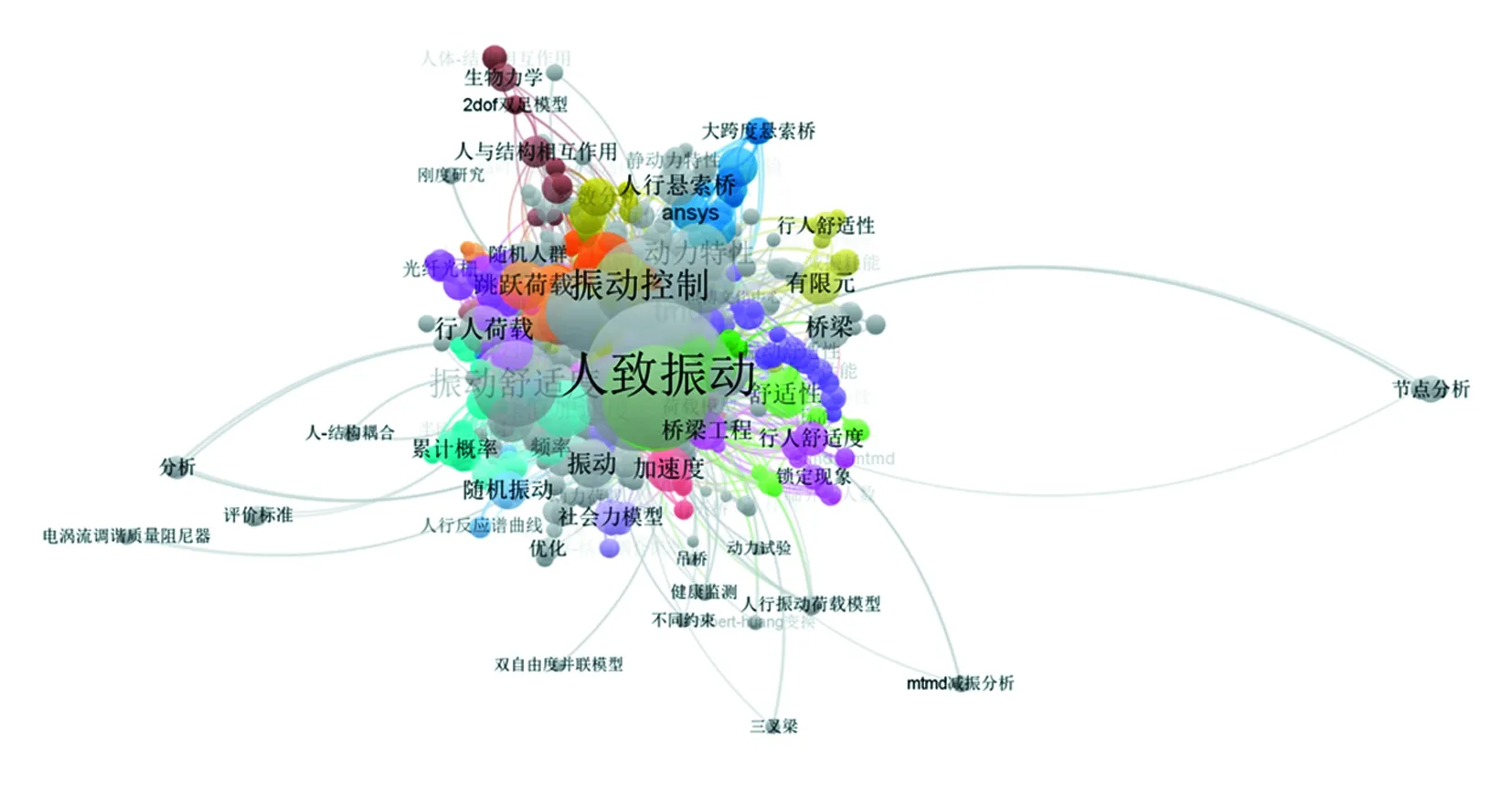
圖1 有關人致振動研究主題分布(截至2021年2月5日)

1 測試方案

為分析人腿荷載隨跳躍頻率的變化規律， 對所招募的300個成年志愿者進行了測力臺跳躍實驗，其中男性184人，女性116人，該實驗在江蘇省裝配式結構實驗室內共花費1個月時長，儀器采用安徽埃力智能科技有限公司的多維測力系統，其中測力臺長寬均為60 cm，厚10 cm，采樣頻率為1000 Hz，測試指導節拍器最低頻率為1 Hz，每間隔0.5 Hz增加一組測試，直到3 Hz結束，共由5組頻率構成。考慮到受試者在跳躍過程中可能會出現跟拍不穩定情況，在測試之前給予受試者適當準備時間，跳躍受試者需要做到全身放松，當聽到開始指令后從地面上跳至測試板中央。起跳騰空過程中腳掌離地幅度要明顯，不能出現腳不離地的假跳狀態，落地時腳掌呈完全著地的狀態，跳躍過程中要求受試者盡量與節拍器保持同步連續的原地跳躍。在進行過一個頻率的跳躍以后測試人員需要短暫的停歇以恢復到正常體力后進入下一個頻率測試。雖然受試者在測試前進行了跟拍訓練以盡可能獲得與節拍頻率一致的跳躍節奏，然而由于個人對節拍器的跟蹤差異導致實測獲得頻率與節拍器頻率存在一定偏差。如圖2所示為測試現場的照片，每個跳躍動作可分為起跳，離地和落地三個基本動作過程。

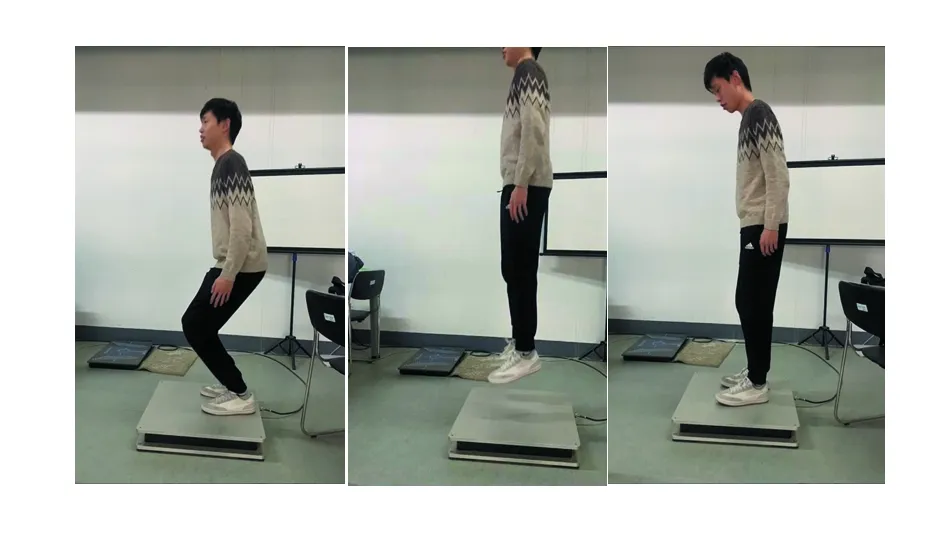
圖2 測試現場照片

圖3所示為典型的6個不同荷載持續時段的荷載形狀曲線，圖中Fz表示跳躍試驗所得荷載，G為人體重量，h為人體身高，m為人體質量。由圖3可知隨著足底觸地時間長從1 s縮短到0.25 s附近，跳躍荷載曲線由雙峰值逐漸過渡到單峰值。出現雙峰曲線是由于測試人員在較低的頻率下落地時腳尖與腳跟非同時落地造成的，可見當人體跳躍較慢時，整個腳底板并不是同時落地。隨著人足與測力板的接觸時間變短，Fz/G的值，即荷載放大系數逐漸增大，且荷載曲線由雙峰形狀逐漸過渡到單峰形狀，人在較高頻率跳躍時，整個足底面是同時落地。

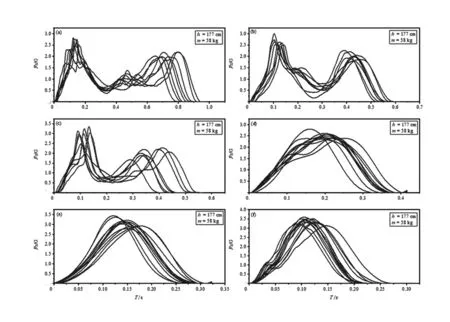
圖3 典型的跳躍荷載曲線

2 樣本統計特征

如圖4所示,對男性志愿者身高和體重的統計特征分析，其中男性身高介于159～191 cm，體重介于48～106 kg，兩者都服從正態分布，其均值分別為176.4 cm和73.5 kg，標準差分別為6.8 cm和14.3 kg。相比于男性，女性志愿者的身高和體重(見圖5)都顯著低于男性志愿者，其身高和體重均值分別為163.8 cm，58.5 kg，標準差分別為5.6 cm和9.1 kg，由于女性志愿者要少于男性志愿者，其身體和體重比男性志愿者離散性高。女性志愿者身高和體重區間范圍分別在148～175 cm以及39～106 kg。由女性身高與體重概率密度分布圖知，約64%女性的身高分布在160～170 cm；約52%的女性體重分布在50～70 kg。女性志愿者身高相對男性更集中，較大部分分布在平均身高附近，而男性身高相對較為分散。同樣女性志愿者體重相對男性體重分布更為集中，且在大多分布在平均值附近，而男性體重相對較為分散。

圖4 男性身高與體重概率密度分布

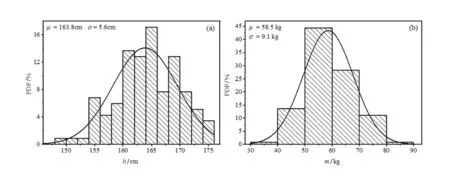
圖5 女性身高與體重概率密度分布

圖6(a)為測試志愿者身高概率累積分布比較，左右側兩條線分別為女性與男性志愿者分布，二者累積分布函數基本平行，可見男性身高普遍較女性高，女性志愿者身高在最初的145～155 cm上升較平緩，而男性志愿者在170～175 cm的區間內數據上升較平緩，說明在最初區間內身高占總體比例較少；隨后女性身高在155～170 cm區間內急劇上升，該區間內女性身高占總體比例迅速增大。男性身高在175～185 cm的區間內數據上升較快，說明在該區間內男性身高占總體比例增大；在185～190 cm區間內上升變得平緩，男生身高在此區間占總體比例較少。圖6(b)為男性與女性體重概率累積分布比較，男性體重在48～90 kg的區間內隨著體重的增加曲線的坡度急劇上升，說明在該區間內男性體重占總體比例較大；在90～150 kg區間內男性體重占總體數據上升較平緩，男生體重在此區間占總體比例較少。女性體重在40～50 kg區間內數據上升較平緩，說明在該區間內女性體重占總體比例較少；在50～70 kg區間內女性體重數據上升急，說明在該區間內女性體重占總體比例較大。

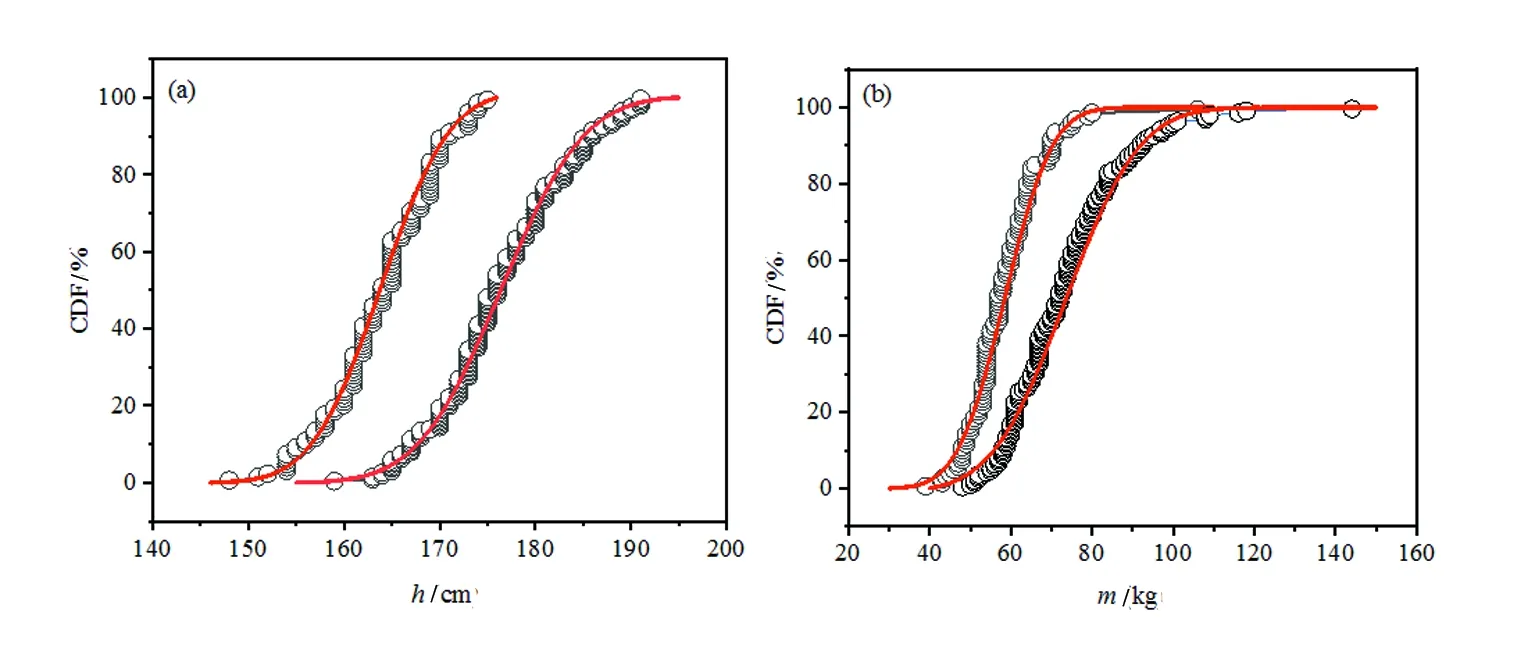
圖6 志愿者身體特征概率累積分布比較

如圖7所示為所有志愿者身高-體重線性擬合。圖中橫縱軸分別為人體身高和體重數據。從圖7可知人體身高值增大時，體重值也在增大，兩者具有較強的正相關性。分析獲得其相關系數為0.576 58，線性方程m=0.95h-94.8，其中該方程的截距誤差范圍在±13.337 21之間，斜率誤差范圍在±0.077 64之間，擬合優度R2為0.332 44，這反映了人體質量的波動有33.244%能被身高h的波動所控制。

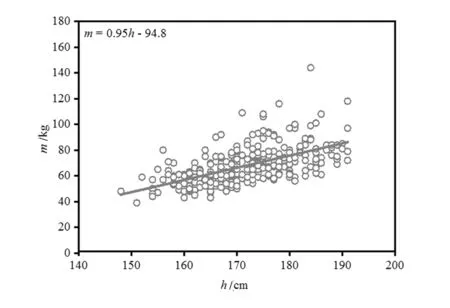
圖7 人體身高-質量的線性擬合

3 跳躍荷載統計特征

圖8為1 Hz節拍頻率下人的跳躍頻率概率密度分布和概率累積分布，該節拍頻率下人體跳躍頻率范圍在0.5～2.6 Hz，均值為12.4 Hz，方差為0.199 Hz。由圖8(a)可知主要頻率集中在1.0～1.4 Hz，其對應概率累積分布圖在0.4～1.0 Hz內線條迅速上升，說明人在1 Hz節拍下跳躍概率較大。而當節拍頻率調高到1.5 Hz后，人體跳躍頻率均值和方差分別為1.87 Hz和0.407 Hz(圖9)，跳躍頻率段主要集中在1.5～2.0 Hz范圍內，人的跳躍頻率微高于節拍頻率。由概率累積分布圖9(b)可知，在0.5～1.5 Hz及2.5～4.5 Hz范圍內數值上升緩慢擬合線條接近一條水平直線，說明在該區間內頻率占比較少；在1.5～2.0 Hz頻率內的曲線上升急促，該區間段的激勵頻率占總體比例較大。當節拍頻率進一步上升到2.0 Hz時，人體跳躍頻率均值與方差分別為2.82 Hz和0.507 Hz(見圖10)。由跳躍頻率的概率密度分布圖可知激勵頻率主要集中在2.5～3 Hz范圍內，人體跳躍節奏高于節拍器頻率。由圖10(b)累積分布圖可知，在1.1～2.5 Hz及3.5～5.1 Hz范圍內數值上升緩慢擬合線條接近一條水平直線，說明在該區間內跳躍頻率占比很少；當激勵頻率增加到2.5～3.5 Hz區間時曲線急促上升，該區間激勵頻率占總體比例最大。如圖11為2.5 Hz節拍頻率下的人體跳躍頻率概率密度分布與累積分布圖，其均值和方差分別為3.44 Hz和0.557 Hz。主要激勵頻率分布在2.5～4 Hz范圍內，頻率均值大于節拍頻率。當節拍器頻率增加到3 Hz時，人體跳躍激勵頻率區間范圍分布于1.6～5.7 Hz內(圖12)。其均值和方差分別為4.29 Hz和0.749 Hz。主要激勵頻率數據分布于3.5～5.0 Hz范圍內，可見高頻時人的跳躍節奏明顯快于節拍器頻率。由于圖12(b)可知，激勵頻率在2.5～3.5 Hz區間內曲線上升緩慢，隨著激勵頻率增高概率分布的曲線上升并未如同前4個頻率上升的急促，該節拍頻率下人的跳躍節奏顯著要快于節拍器頻率。

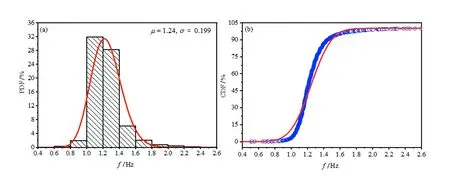
圖8 1 Hz節拍下的激勵頻率統計分布

圖9 1.5 Hz節拍下的激勵頻率統計分布

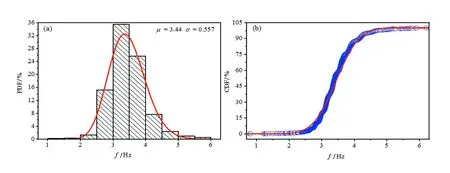
圖11 2.5 Hz節拍下的激勵頻率統計分布

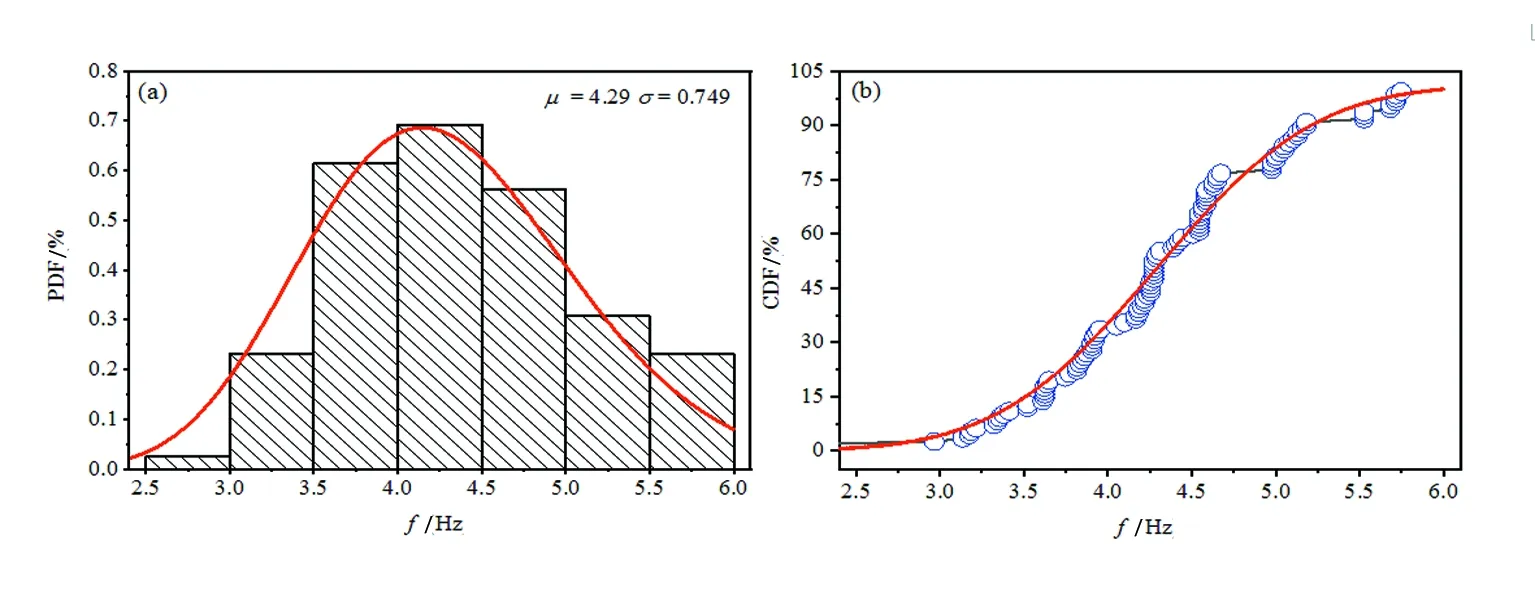
圖12 3 Hz節拍下的激勵頻率統計分布

4 荷載特征分析

為描述人體跳躍豎向荷載，采用如式1所示的傅里葉級數模型表示，其中G為人體重量，β為荷載放大系數，αi為第i階荷載因子，f為激勵頻率。通過回歸分析對前6階荷載因子進行擬合分析結果如圖13所示。其中α1=1.07+0.37f，擬合優度值R2=0.75，二階及以上荷載因子與激勵頻率呈現三次多項式擬合關系，其中后五階擬合優度值分別為0.35， 0.79， 0.30， 0.52， 0.18，奇數階擬合優度普遍高于偶數階擬合優度值，由此可見人體跳躍荷載由奇數階荷載因子控制。此外通過對荷載放大系數的極值進行回歸分析獲得激勵頻率與放大系數極值的關系為βm=3.251-0.463f+0.144f2=0.114(f-2.03)2+2.78，當人體激勵頻率接近2.03 Hz時放大系數極值最小，其值2.78，而遠離該頻率點時，放大系數極值都會增大，由此可見在跳躍荷載設計時放大系數不應小于2.78，且需要考慮人的激勵頻率區間。

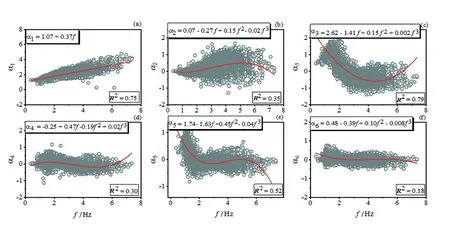
圖13 前六激勵荷載因子擬合曲線

圖14 激勵放大系數擬合曲線

最后利用式1所示的傅里葉級數荷載模型與實測跳躍荷載曲線比較，如圖15所示黑色散點跳躍試驗所得曲線與傅里葉級數模型的紅色曲線進行對比的結果，表明試驗曲線與擬合曲線的重合度較好。從圖15(a)(b)(c)中可觀察到出現了兩個峰值，由于受試者在頻率較低的情況下跳躍時，腳尖與腳跟先后落地時間間隔較長而出現了兩個峰值。人體跳躍在低頻率和高頻率的情況下，荷載曲線形狀顯著不同，可見本文所建議的模型以及荷載因子參數能夠有效表征不同跳躍頻率激勵下的人體跳躍荷載。

圖15 激勵放大系數擬合曲線

5 結論

本研究系統開展了大樣本單人跳躍荷載測試工作，人體特征分析表明受試者體重與身高呈較強的線性相關性；雙足跳躍荷載統計特征分析表明人在不同跳躍頻率都服從正態分布；利用傅里葉級數模型對實測人體跳躍荷載回歸分析表明：除了1階動力因子α1隨激勵頻率的增加呈線性增加，其他高階動力因子都表現出較強的非線性特征；對跳躍激勵放大系數(跳躍荷載與人體重量比值)分析表明：當跳躍荷載為2.03 Hz，該系數最小，跳躍荷載激勵最小；通過對前6階荷載因子和荷載放大系數的擬合曲線發現文中所建議單人跳躍激勵模型能較好地反映實際人體跳躍荷載，該跳躍荷載模型能為人致結構振動工程設計和分析提供參考依據。