關于H-矩陣Hadamard積的一個行列式不等式
劉俊同,李 龍
(1. 阜陽師范大學數學與統計學院,安徽阜陽 236041;2. 阜陽一中,安徽阜陽 236000)
0 引言
H-矩陣是一類特殊矩陣,它在計算數學、經濟學、管理科學、神經網絡和控制論等諸多學科都有著重要的應用.而矩陣的Hadamard積是一種特殊的矩陣乘積,它被廣泛的應用于量子計算、編碼理論、物理學和區組設計等問題中.基于這些重要的應用背景,H-矩陣的Hadamard積的特征值和行列式問題一直備受國內外專家學者的關注,關于這方面更多的內容請參見文獻[1-9].
Oppenheim于1930年證明了下述不等式(見文獻[1,P509]):給定兩個n級半正定矩陣A和B,則有
(1)
其中A°B表示矩陣A和B的Hadamard積,上述不等式稱為Oppenheim行列式不等式.
Lynn[2]和Ando[3]分別推廣了不等式(1),它們差不多同時得到如下結果:給定兩個n級半正定矩陣A和B,則有
等價地
(2)
Li 和Li在文獻[4]中證明了如下結果:給定兩個n級實的H-矩陣A和B,則有
(3)
其中Ak表示矩陣A的第k個順序主子陣
Chen在文獻[5]中推廣了上述不等式(3),得到了如下更整齊的結果:給定兩個n級H-矩陣A和B,則有
(4)
其中μ(A)表示矩陣A的比較矩陣,具體定義見下一小節.
本文將利用數學歸納法、M-矩陣和H-矩陣的基本理論以及不等式的構造和放縮技巧推廣不等式(4)到更一般形式.
1 符號、定義和引理
為了表述方便,首先介紹一些符號.設Cm×n(Rm×n)表示m×n復(實)矩陣的全體組成的集合,A≥0(A>0)表示矩陣A的所有元素都是非負(正)的 .對于兩個相同級數的矩陣A和B,用A°B表示矩陣A和B的Hadamard積,設A=(aij)∈Cn×n,常用Ak(k=1,2,…,n)表示矩陣A的第k個順序主子矩陣,Aα表示矩陣A的指標位于α?{1,2,…,n}的主子矩陣.
定義1[10]稱集合
Zn×n={A=(aij)∈Rn×n:aij≤0,i≠j,i,j∈{1,2,…,n}}
中的矩陣為Z-矩陣.
易知A=(aij)∈Rn×n是Z-矩陣的充分必要條件是存在α∈R,P∈Rn×n,且P≥0,使得A=αE-P.
定義2[10]設A=(aij)∈Cn×n,若A是Z-矩陣,且對任意的k=1,2,…,n,都有第k個順序主子矩陣的行列式|Ak|>0,則稱矩陣A是M-矩陣.

則稱μ(A)為矩陣A的比較矩陣.
定義4[10]設A=(aij)∈Cn×n,若矩陣A的比較矩陣是M-矩陣,則稱A是H-矩陣.
易證M-矩陣(H-矩陣)的每一個主子矩陣還是M-矩陣(H-矩陣).
為了陳述和證明主要結果,我們需要下述引理
引理1[3]設A=(aij)∈Rn×n是一個M-矩陣,若
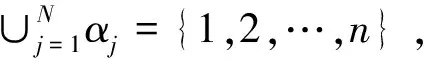
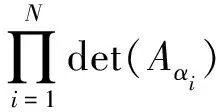
特別地,有
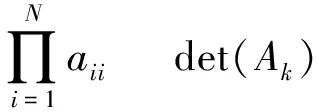
(5)
引理2[2]若A和B是兩個n級H-矩陣,且C=A°B,則矩陣C也是一個n級H-矩陣.
引理3 設a和b是兩個實數,且有a≥1,b≥1,則有ab≥a+b-1.
證明:因為a≥1,b≥1,于是有
ab-a-b+1=(a-1)(b-1)≥0
所以,有
ab≥a+b-1
2 主要結果
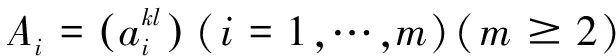
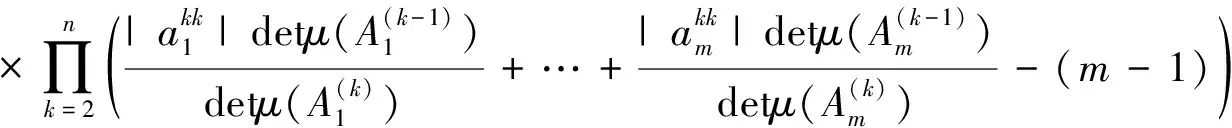
證明由引理2,知A1°…°Am仍是H-矩陣,對矩陣的個數k使用歸納證明.當k=2時,定理歸結于Chen 的結果(4),假設當k=m-1時,定理成立,即

成立,下證當k=m時,定理也成立,即證
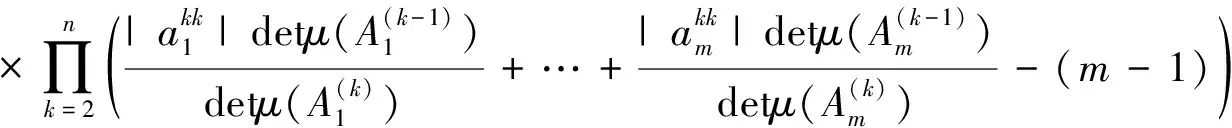
通過不等式(4),有
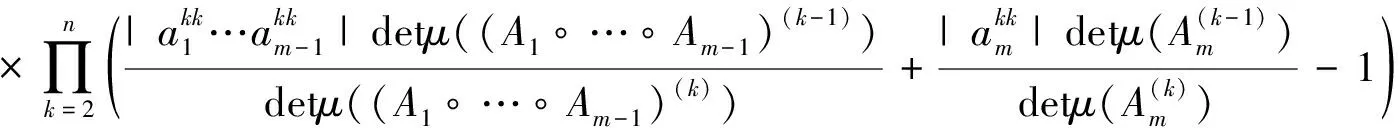
應用歸納假設,則有
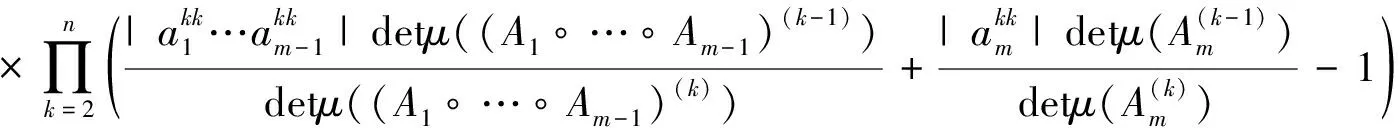
(6)
記
(7)
(8)
應用引理1,通過不等式(5),有
(9)
因此有,
xk≥1,yk≥1
利用引理3,有
xkyk≥xk+yk-1
(10)
結合不等式(7)、(8)、(9)和(10),不等式(6)進一步可化為
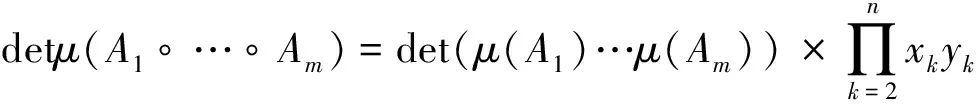
3 小結
本文結合H-矩陣的基本理論、矩陣Hadamard積的性質以及不等式的構造和放縮技巧,證明了H-矩陣Hadamard積行列式不等式的一個重要結果,推廣了已有文獻的結果.H-矩陣是一類應用范圍極其廣泛的矩陣,對H-矩陣理論展開研究一方面可以豐富H-矩陣理論,另一方面對矩陣理論也有一定的拓展意義.

