基于卷積神經(jīng)網(wǎng)絡(luò)的運動輔助決策系統(tǒng)設(shè)計

查 毅，馮宏偉

（1.西安文理學(xué)院，陜西 西安 710065；2.西北大學(xué)，陜西 西安 710069）

運動訓(xùn)練輔助決策系統(tǒng)，對于輔助運動訓(xùn)練管理者預(yù)測、決策、評價與提高運動員的綜合訓(xùn)練水平具有重要意義。但該系統(tǒng)是一種具有高度復(fù)雜性的智能數(shù)據(jù)分析處理平臺，其核心技術(shù)是人體姿勢的精確識別技術(shù)。近年來，人體姿勢識別技術(shù)已逐漸成熟，而衡量姿勢識別算法性能的關(guān)鍵參數(shù)是實時性與準(zhǔn)確性[1]。隨著人工智能技術(shù)的發(fā)展，神經(jīng)網(wǎng)絡(luò)的深度學(xué)習(xí)被廣泛應(yīng)用于多個領(lǐng)域[2]。因反向傳播（BP）神經(jīng)網(wǎng)絡(luò)具有適應(yīng)性高、原理簡單、易于實現(xiàn)等優(yōu)點，通常被應(yīng)用于手勢和動作姿態(tài)識別[3]。

文中基于OpenPose 與神經(jīng)網(wǎng)絡(luò)進(jìn)行了姿勢識別與運動狀態(tài)分析，基本思想是對來自視覺相機的人體姿勢進(jìn)行識別、分類與存儲[4]。通過使用卷積神經(jīng)網(wǎng)絡(luò)的方法[5]，對抽象為優(yōu)化問題的運動數(shù)據(jù)進(jìn)行分析[6]。

1 人體姿態(tài)識別建模

在姿勢判斷中定義人體姿勢描述符至關(guān)重要，因此必須選擇一種適當(dāng)?shù)臄?shù)據(jù)集來精確描繪每個動作。通過需求分析可知，姿勢描述方法必須滿足以下要求：1）數(shù)據(jù)冗余少[7]；2）魯棒性高[8]；3）傳感器方向不變性[9]；4）信號連續(xù)性。

基于上述考慮，對關(guān)節(jié)數(shù)據(jù)的處理進(jìn)行重點設(shè)計，系統(tǒng)架構(gòu)如圖1 所示。

圖1 系統(tǒng)結(jié)構(gòu)

1.1 關(guān)節(jié)位置確定

文中使用OpenPose 展開設(shè)計，其是一種基于OpenCV 與Caffe 的C++實時多人關(guān)鍵點檢測和多線程庫，可實現(xiàn)在單個圖像上動態(tài)聯(lián)合檢測人體手部和面部最多130 個關(guān)鍵點。

OpenPose 提供了18 個身體關(guān)節(jié)的實時位置，如圖2 所示。文中以JSON 格式獲取包含身體部位位置和檢測置信度的數(shù)據(jù)。這18 個關(guān)節(jié)坐標(biāo)能夠完整且獨特地表示每個姿勢，且可確保較低的計算復(fù)雜度。但由于這些基于像素的描述符在幾何變換過程中會發(fā)生變化，因此難以定義距離度量，文中使用關(guān)節(jié)軌跡估計的方法解決該問題。

圖2 身體關(guān)節(jié)圖

1.2 關(guān)節(jié)軌跡估計

由于單張圖片的信息存在不連續(xù)性，因此無法使用連續(xù)的關(guān)節(jié)位置信息，該次選擇運動軌跡來解決此問題。運動軌跡定義為在某些順序幀之間通過相同關(guān)節(jié)連接的曲線，身體運動軌跡描述符不需要進(jìn)行標(biāo)準(zhǔn)化，且可以適應(yīng)不同的情況。

為了使系統(tǒng)對輸入噪聲具有魯棒性，將軌跡方程細(xì)化為Bezier 曲線。對于某個關(guān)節(jié)的第k個位置，其噪聲信息可表示為qk=(xk,yk),(0 ≤k≤n)。混 合上述坐標(biāo)可以生成位置矢量Q(i)，如式（1）所示：

其中，貝塞爾混合函數(shù)BEZk,n(i)是伯恩斯坦多項式，如式（2）所示：

其中，C(n,k)是二項式系數(shù)：

由于貝塞爾曲線是一種近似曲線而不是插值曲線，因此計算貝塞爾曲線有助于平滑軌跡，并減少輸入噪聲的影響。

2 基于CNN的運動分析算法設(shè)計

對于上文中建立的關(guān)節(jié)分類模型，抽象出常用的優(yōu)化問題，如下式所示：

其中，xi是研究變量，即各個關(guān)節(jié)的離散化函數(shù)，其變量范圍是[ai,bi]，r是變量數(shù)。

對神經(jīng)網(wǎng)絡(luò)算法的基本步驟分別進(jìn)行了重新設(shè)計：

1）個體編碼[10]。通常通過二進(jìn)制編碼與實數(shù)編碼來實現(xiàn)，該文采用實數(shù)編碼方法對xi進(jìn)行編碼，xi代表BP 神經(jīng)網(wǎng)絡(luò)的權(quán)重值和閾值。編碼長度為14×13+13+13×5+5=265，種群大小為15，最大遺傳代數(shù)為20。

2）確定適應(yīng)度函數(shù)[11]。BP 神經(jīng)網(wǎng)絡(luò)的實際輸出為Ti，預(yù)期輸出為Oi，因此BP 神經(jīng)網(wǎng)絡(luò)誤差定義為：

由于該文的目標(biāo)最優(yōu)解是一個最小化問題，因此選擇BP 神經(jīng)網(wǎng)絡(luò)的倒數(shù)作為適應(yīng)度值，即：

3）選擇過程[12]。選擇過程是人口演變的重要組成部分，文中將輪盤賭選擇方法與精英選擇方法相結(jié)合，產(chǎn)生下一代個體。適應(yīng)度值最大的個體不進(jìn)行交叉和變異操作，而是通過遺傳直接轉(zhuǎn)移給下一代。使用輪盤賭選擇方法選擇剩下的個體，每個個體被選為下一代的概率為：

4）交叉操作。交叉操作在遺傳算法中起著重要作用，其與遺傳算法的搜索能力密切相關(guān)[13]。采用模擬二進(jìn)制分頻器實現(xiàn)分頻器運算，首先可通過下式計算分頻系數(shù)ri：

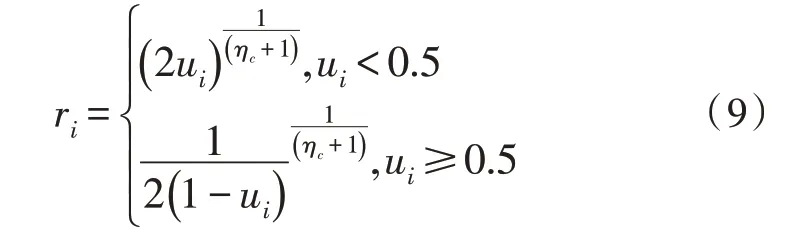
其中，ui是屬于[0，1]的隨機數(shù)，i∈[0,length-1],ηc=10，是父代個體p1和p2通過下式確定的個體后代[14]：

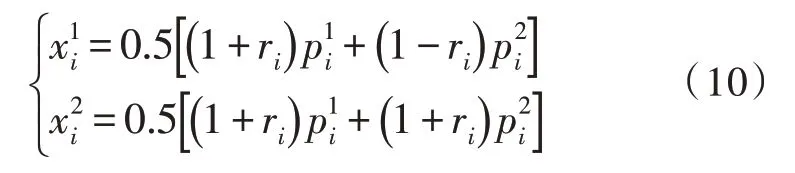
5）變異運算[15]。變異的主要作用是引入變異算子以生成新的個體，并豐富模式的多樣性。采用變化規(guī)律的多項式形式，且可以通過下式獲得變化系數(shù)δ：

其中，u是[0，1]內(nèi)的隨機數(shù)，ηm通常也為隨機常數(shù)，該文定義ηm=10。突變后的每個單獨基因可表示為：

其中，Δmax是最大變化范圍。

6）進(jìn)化停止標(biāo)準(zhǔn)[16]。當(dāng)?shù)螖?shù)k到達(dá)閾值或連續(xù)5 個迭代后，最佳個體保持不變，則遺傳算法結(jié)束并輸出最優(yōu)解。

神經(jīng)網(wǎng)絡(luò)計算得出最優(yōu)結(jié)果的速度較慢，因此將混沌擾動添加到遺傳種群變量中，以加快優(yōu)化速度。假設(shè)優(yōu)化個體為，在對遺傳算法進(jìn)行選擇、交叉和變異后，采用混沌算法對該個體進(jìn)行擾動。其擾動公式為：

其中，δk是第k次迭代的混沌擾動矢量，δ?是最優(yōu)解的矢量，是隨機混沌擾動向量。為獲得α，使用可變尺度混沌方法，具體方程為：

在迭代開始時，α值較大，且混沌遍歷空間較大。因此，在這種情況下進(jìn)行了粗略搜索。隨著迭代次數(shù)的增加，α的值逐漸減小，詳細(xì)搜索工作正式開始。

每次迭代后，計算新個體的適應(yīng)度值。當(dāng)其適應(yīng)度值大于原始個體時，該算法將選擇受混亂影響的新個體作為當(dāng)前最佳個體；否則，迭代將繼續(xù)。若在連續(xù)5 次迭代后最佳個體值未有變化，則迭代將停止。最優(yōu)解將被輸出并從混沌空間映射到解空間，映射公式如下：

3 實驗驗證

為驗證運動輔助決策系統(tǒng)，在Ubuntu 18.04 計算機操作系統(tǒng)中進(jìn)行驗證。系統(tǒng)搭載在Intel 10700K CPU、NVIDIA 3070Ti 圖形處理器上，配置CUDA 與CUDNN 架構(gòu)。分別采用BP 神經(jīng)網(wǎng)絡(luò)、遺傳算法(GA)改進(jìn)的BP 神經(jīng)網(wǎng)絡(luò)以及卷積遺傳算法（CGA）改進(jìn)的BP 神經(jīng)網(wǎng)絡(luò)來復(fù)現(xiàn)算法，這3 個網(wǎng)絡(luò)的學(xué)習(xí)誤差下降曲線如圖3～5 所示。

圖3 BP網(wǎng)絡(luò)學(xué)習(xí)曲線

在圖3 中，使用BP 神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)5 000 次后，最終系統(tǒng)誤差為0.005 655 8，誤差變化率接近于0，但落入了局部最優(yōu)狀態(tài)。

在圖4中，GA 修改了BP神經(jīng)網(wǎng)絡(luò)并學(xué)習(xí)了5 000次，系統(tǒng)誤差為0.000 418。結(jié)果較為接近期望誤差，且誤差率不為0。這意味著其不會落入局部最小值，但學(xué)習(xí)時間更長。

圖4 遺傳算法改進(jìn)的BP網(wǎng)絡(luò)學(xué)習(xí)曲線

在圖5 中，CGA 修改后的BP 神經(jīng)網(wǎng)絡(luò)僅學(xué)習(xí)608 次就達(dá)到了理想誤差，學(xué)習(xí)時間大幅減少，最終誤差小于GA改進(jìn)的BP神經(jīng)網(wǎng)絡(luò)結(jié)果。從以上數(shù)據(jù)分析可看出，CGA 可優(yōu)化BP 神經(jīng)網(wǎng)絡(luò)，避免神經(jīng)網(wǎng)絡(luò)陷入局部最小值，能夠有效提高識別速度與準(zhǔn)確性。

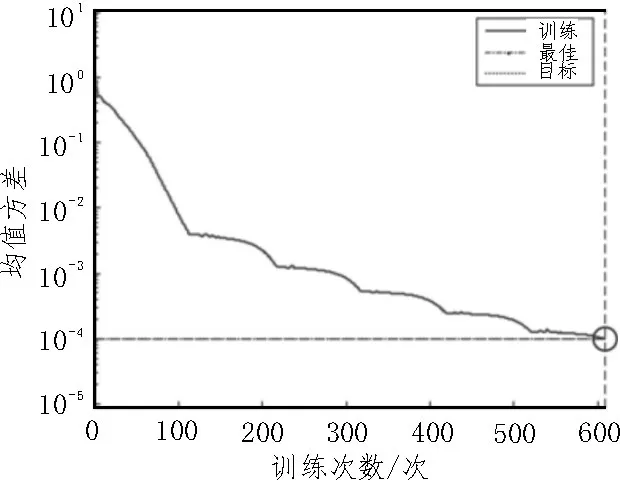
圖5 CGA改進(jìn)的BP網(wǎng)絡(luò)學(xué)習(xí)曲線

在訓(xùn)練完成的基礎(chǔ)上，使用視覺相機進(jìn)行實際實驗驗證，測試員佩戴時獲得的信號數(shù)據(jù)是一個連續(xù)數(shù)據(jù)流。在應(yīng)用程序開發(fā)過程中，使用計時器對連續(xù)數(shù)據(jù)流進(jìn)行采樣，并獲得離散的靜態(tài)姿勢。測得的姿勢與數(shù)據(jù)庫中現(xiàn)有的數(shù)據(jù)模板進(jìn)行比對，然后輸出最佳解決方案。為避免外界干擾，設(shè)置了錯誤閾值。當(dāng)誤差小于閾值時，程序開始識別無效姿勢。16 s 的姿勢匹配數(shù)據(jù)流曲線如圖6 所示。Matlab 的仿真結(jié)果表明，當(dāng)誤差小于0.1 時，兩個連續(xù)的姿勢段可能會產(chǎn)生干擾現(xiàn)象；當(dāng)誤差大于0.1 時，所有姿勢均可正常識別，因此將0.1 設(shè)置為錯誤閾值。

圖6 姿勢識別匹配曲線

基于數(shù)據(jù)手套和可穿戴傳感器的姿勢識別平臺是采用VS2008 MFC 商用套件開發(fā)的，識別結(jié)果如圖7 所示。

圖7 姿勢識別結(jié)果

在此基礎(chǔ)上，選擇10 個不同的操作者戴著傳感器進(jìn)行姿勢識別，每個人重復(fù)相同姿勢30 次，記錄正確識別時間和平均識別率。統(tǒng)計結(jié)果表明，平均識別準(zhǔn)確率可達(dá)到98.67%。

4 結(jié)束語

該文綜合了混沌算法與遺傳算法，優(yōu)化了神經(jīng)網(wǎng)絡(luò)，并基于優(yōu)化后的神經(jīng)網(wǎng)絡(luò)實現(xiàn)了精確的人體運動姿勢識別。所提出的改進(jìn)算法首先建立神經(jīng)網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu)，對神經(jīng)網(wǎng)絡(luò)的權(quán)重和閾值進(jìn)行編碼以形成單個物種，并通過遺傳算法進(jìn)行選擇、交叉和進(jìn)化，獲得最優(yōu)解。從實驗結(jié)果可知，CGA 改進(jìn)的BP神經(jīng)網(wǎng)絡(luò)不僅可以解決容易陷入局部最小值的問題，而且能夠加快收斂速度，明顯提高優(yōu)化神經(jīng)網(wǎng)絡(luò)的精度，對人體姿勢的檢測精確度可提高到98%以上，有效提高了運動輔助決策系統(tǒng)的實時性和識別精度。