87Rb玻色-愛因斯坦凝聚體中雙拉曼相對相位對相干躍遷操控的實驗研究*

周方 文凱 王良偉 劉方德 韓偉 王鵬軍黃良輝 陳良超 孟增明? 張靖

1) (山西大學光電研究所, 量子光學與光量子器件國家重點實驗室, 太原 030006)

2) (山西大學, 極端光學協同創新中心, 太原 030006)

發展了利用兩對拉曼光之間的相對相位精確調控拉曼耦合強度的新方法, 實現了兩個量子態相干躍遷的操控.對兩對拉曼光的光路進行了特殊設計, 從而保證兩對拉曼激光在傳輸過程中的相對相位保持恒定,然后作用到87Rb原子的兩個超精細塞曼能級 | 1,1〉 和 | 1,0〉 上, 實驗觀測了兩個量子態的布居數隨兩對拉曼光之間的相對相位的變化關系.該方法為超冷原子量子模擬實驗提供了一個獨特的操控參量——激光相位, 由此拓展了受激拉曼躍遷的應用范圍, 為研究光與原子相互作用提供了一種新的方法.

1 引 言

受激拉曼躍遷過程具有高度人為可控、多自由度的特性, 通過控制激光的功率、頻率、相位和原子能級構型等可實現受激拉曼躍遷的精確調控[1].該技術可實現原子量子態的相干操控, 而不受自發輻射的影響, 因此該方法在物理和化學等許多領域得到了廣泛應用[2], 如: 物質波原子干涉儀[3,4]、拉曼冷卻[5-8]、量子比特操控[9,10]、量子精密測量[11,12]、量子存儲[13]、手性分子[14,15]等.

近幾年, 在超冷原子系統中利用受激拉曼躍遷過程可以將光的動量傳遞給原子, 先后實現了人造規范勢[16-18]、人造磁場[19]、自旋-軌道耦合[20-22]以及人造維度[23]等, 這極大地拓寬了超冷原子進行量子模擬的能力.激光的相位信息在光與原子耦合方面扮演非常重要的角色.通過控制激光的相位信息可實現對各種新奇的拓撲量子態和拓撲量子相變的操控, 例如: 實現人造垂直塞曼磁場操控狄拉克點處的拓撲能隙[24]、通過調節激光相位實現一維和二維自旋-軌道耦合之間的轉變[25]、利用拉曼激光的拉蓋爾-高斯軌道角動量實現原子的自旋與軌道角動量耦合[26]等.

在超冷原子實驗中, 可通過調節拉曼光強度、雙光子頻率失諧以及相互作用時間來調控原子能級間的布居, 通常利用改變拉曼激光的強度來實現調控拉曼耦合強度, 而本文基于二能級原子, 發展了利用兩對拉曼光之間的相對相位精確控制拉曼耦合強度的新方法, 實現了兩個量子態相干躍遷的操控.利用光學偶極阱實現了87Rb原子玻色-愛因

斯坦凝聚體, 對兩對拉曼激光進行了特殊的光路設計, 使兩對拉曼激光在傳輸過程中相對相位保持穩定, 并可以精確調控, 然后作用到87Rb原子的兩個超精細塞曼能級 | F=1,mF=1〉 和|F=1,mF=0〉上.測量了兩個量子態的布居數隨兩對拉曼光之間的相對相位的變化關系.該技術拓展了受激拉曼躍遷的應用范圍, 為研究光與原子相互作用提供了一種新的方法.

2 理論模型

情況1單受激拉曼過程

圖1(a)為一個簡單的三能級原子系統, 其中|g1〉 和 | g2〉 為原子的兩個基態, |e〉 為原子的激發態,原子初始全部處于基態 | g1〉 , 利用一對同向傳播、頻率分別為 ω1,ω2的紅失諧拉曼光(Raman 1, 2)作用于該三能級原子系統, 由此實現原子在基態之間的拉曼躍遷.ω01和 ω02為原子共振躍遷頻率, 兩束激光的單光子失諧為: Δ1=ω01-ω1,Δ2=ω02-ω2.兩束激光的相位為: φ1=k1·r+φext,φ2=k2·r , 其中 k1,2為激光的波矢; r 為空間坐標;φext為外加的相位.

圖1 (a)單受激拉曼躍遷過程; (b)雙受激拉曼躍遷過程Fig.1.(a) Energy levels and stimulated Raman transitions by using two Raman lasers; (b) energy levels and double stimulated Raman transitions by using four Raman lasers.

利用旋波近似, 三能級原子系統的波函數和薛定諤方程為

式中, A1, A2和 A3是各個量子態的分量; 有效哈密頓量寫為

其中 Ωα=-〈gα|ε?α?d|e〉E0α/? , 為拉比頻率, 其中 α =1,2 , 代表兩個基態能級.Ωα描述了原子從基態 | gα〉 通 過拉曼激光 E0α躍遷到激發態 |e〉 的耦合強度.p為原子的動量, m為原子質量.

實驗中采用遠失諧拉曼過程, 即可絕熱消除激發態( A3), 由此將三能級系統簡化為二能級系統,體系的有效哈密頓量可以寫為

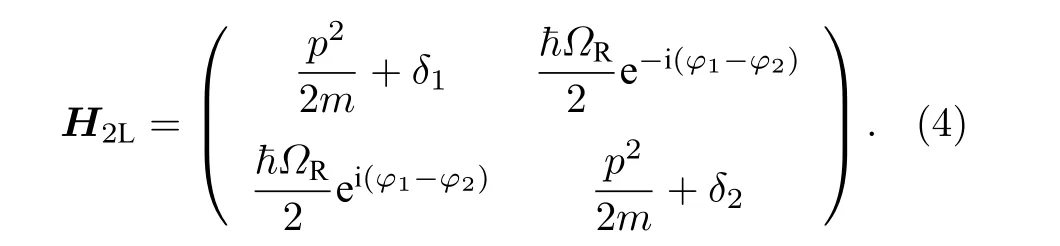
在實驗中, 一對拉曼激光同向傳播并頻率相近, 由此可得相位差:Δφ=φ1-φ2=(k1-k2)·r+φext≈φext.利用幺正變換可消除拉曼光相位差 φext,有效的哈密頓量為[27]

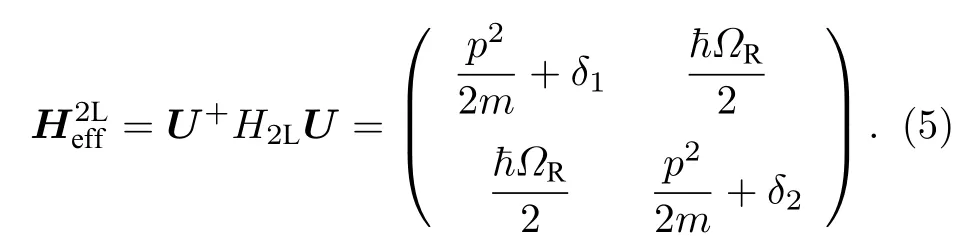
分析可知: 在單受激拉曼過程中, 一對拉曼激光的相位差因可以被規范掉而不影響拉曼耦合強度.圖2(a)為原子在基態 | g2〉 的布居數與相位差Δφ的關系圖, 可以清晰地看出, 原子的躍遷不受拉曼激光相位差的影響.

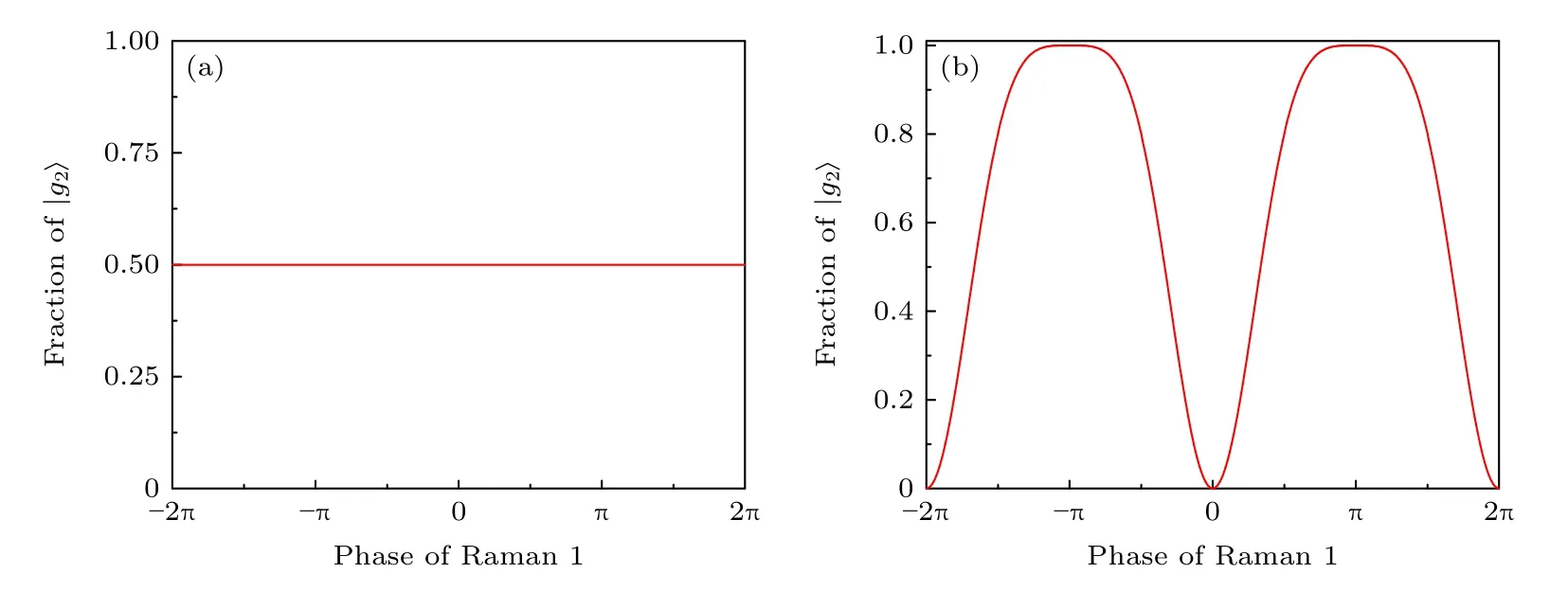
圖2 原子在 | g2〉 態的布居數分布與拉曼光相位差的關系 (a)單受激拉曼過程; (b)雙受激拉曼過程Fig.2.Relationship between the population in | g2〉 and the phase difference of Raman laser: (a) Single stimulated Raman transitions; (b) double stimulated Raman transitions.

情況2雙受激拉曼過程

發展了一種新方法, 通過精確調控拉曼光的相對相位實現對拉曼耦合強度的調控.利用兩對同向傳播的、遠失諧的拉曼光同時作用于三能級原子系統, 構成雙受激拉曼過程, 即: 在情況1的基礎上多注入一對藍失諧拉曼激光Raman 3, 4, 頻率分別為 ω3,ω4, 相 位為 φ3=k3r , φ4=k4r , 失諧 為Δ3=ω01-ω3, Δ4=ω02-ω4, 見圖1(b), 此時系統的有效哈密頓方程可以寫為

式中, δα=?(Δα+ωACα) , α =1,2,3,4 , 其余參數與情況1類似.

在實驗中, 兩對拉曼激光均同向傳播并兩兩頻率相近, 兩對拉曼光的相對相位差為:Δφ=(φ1-φ2)-(φ3-φ4)=(k1-k2)·r+φext-(k3-k4)·r≈φext.在這種情況下, 利用幺正變換可得有效的哈密頓量為

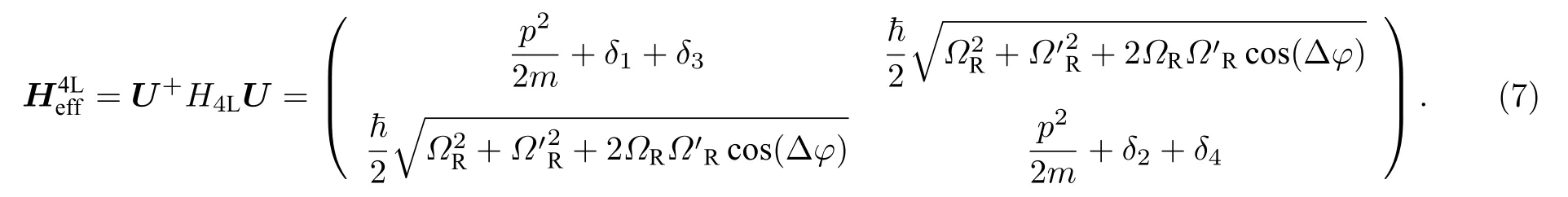
(7)式中幺正矩陣為

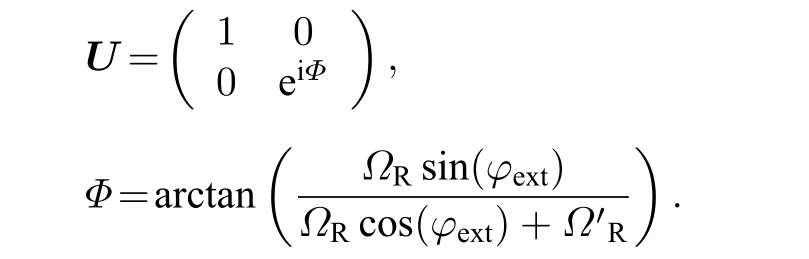
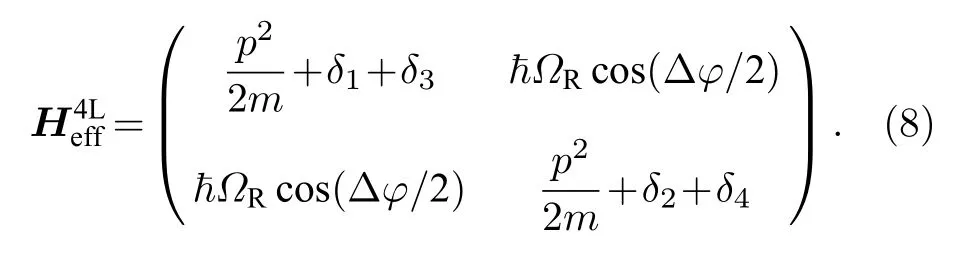
分析可知: 在雙受激拉曼過程中, 兩對拉曼光之間的相對相位差可以精確調控拉曼耦合強度, 見圖2(b), 可以清晰地看出, 當兩對拉曼激光同時作用原子時, 它們之間的相對相位差 Δ φ 可以調控原子在基態 | g2〉 的布居數.由此說明在雙受激拉曼過程中, 兩對拉曼光之間的相對相位差發揮著非常重要的角色, 在實驗中需要設計恒定的光路, 從而避免額外的相對相位抖動影響拉曼耦合過程.

3 實驗過程

圖3為產生拉曼激光的實驗光路圖, 為了獲得兩對拉曼激光, 利用兩臺可調諧鈦寶石激光器1和2、兩個聲光調制器(acoustic optical modulator,AOM)、兩個功率分配器(power splitter, PS)和一臺四通道信號源.信號源的1, 2端口分別輸出頻率為f1= 76 MHz和f2= 98.305 MHz的射頻信號, 將兩路信號接到PS的兩個輸入端口, 然后將PS的輸出接到AOM的射頻輸入端.鈦寶石激光器1產生一束紅失諧的激光, 頻率為fC=384.0000 THz, 然后將其注入到AOM中, 由此產生一對空間分離的+1級的拉曼激光: Raman 1, 2.通過類似的辦法, 鈦寶石激光器2產生一束藍失諧的激光, 頻率為fS= 384.2484 THz, 通過AOM后就可以得到+1級的另一對拉曼激光: Raman 3, 4.兩對拉曼激光的頻率與87Rb原子超精細能級分裂的對應關系見圖4.

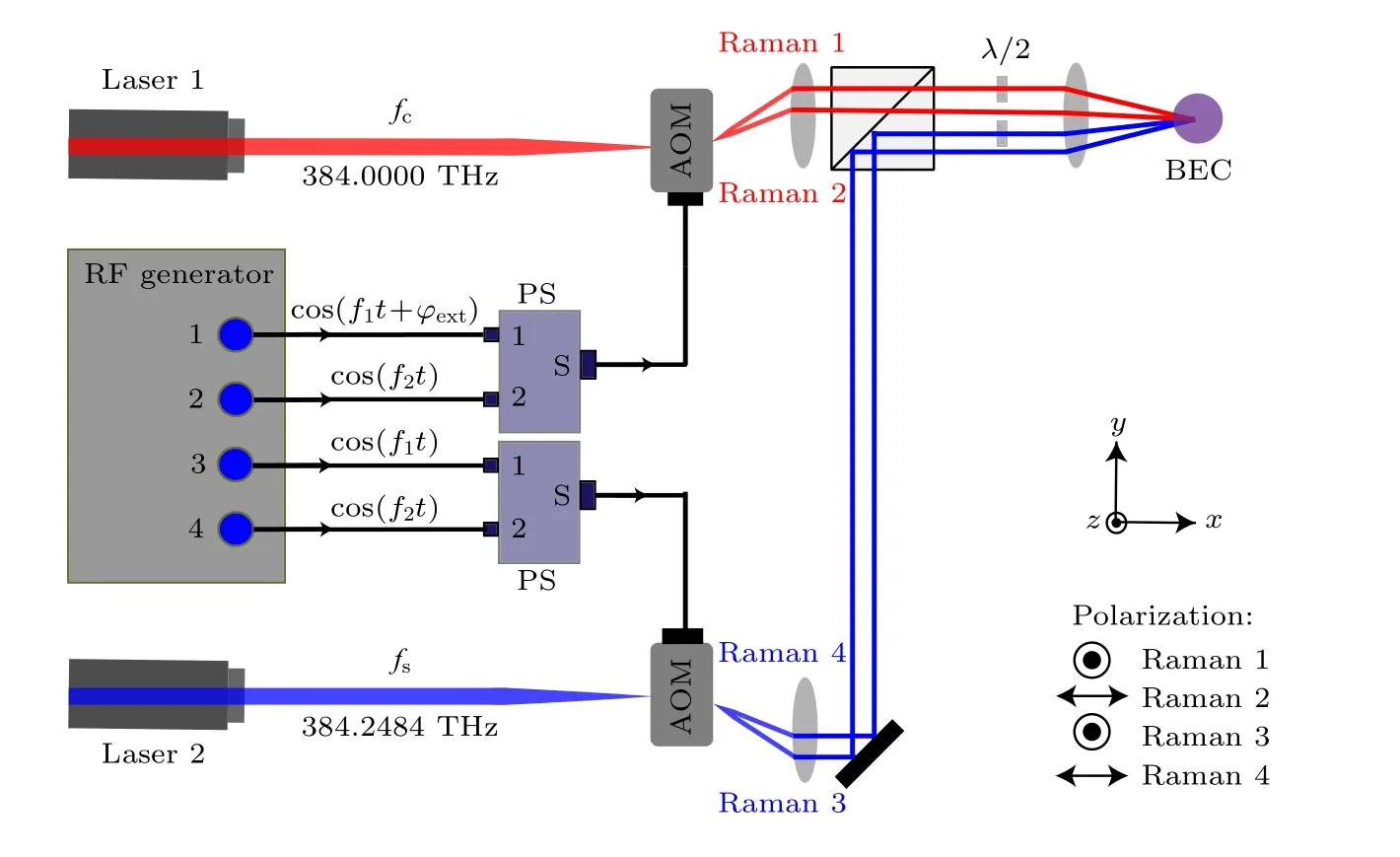
圖3 實驗光路圖Fig.3.Experimental optical diagram.

圖4 三能級87Rb原子系統中的拉曼躍遷示意圖Fig.4.Schematic diagram of Raman transitions in three level 87Rb atomic system.

為了避免光程差導致相對相位的抖動, 一對拉曼光Raman 1, 2從AOM出射后, 同時入射到偏振分束器上(polarizing beam splitter, PBS).另一對拉曼光Raman 3, 4從AOM出射后, 利用一個鏡片反射到PBS上, 與Raman 1, 2合束后照射到原子上.

實驗中, 利用AOM將射頻相位 φext加載到激光Raman 1上( φext∈[-2π,2π] ), 在 情 況1和2中, 通過調節射頻相位 φext即可實現調控一對或兩對拉曼光之間的相對相位, 進而研究相對相位與原子拉曼耦合強度的對應關系.

為了實現原子的拉曼躍遷, 實驗中Raman 1和3為垂直偏振, Raman 2和4為水平偏振, 另外,磁場的量化軸選為z軸, 詳細的光路設計見圖3.

實驗中, 首先在反亥姆霍茲線圈和532 nm藍失諧激光組合的光塞磁阱中運用射頻蒸發冷卻技術對87Rb原子進行預冷卻, 當87Rb原子溫度到達5 μK時, 將預冷卻的原子樣品絕熱裝載到光學偶極阱中, 光學偶極阱是由兩束波長為1064 nm的紅外激光在x-y平面90°交叉構成, 兩束激光頻率相差10 MHz, 在原子云處的腰斑直徑大約為200 μm, 最終通過光阱蒸發冷卻實現87Rb原子的玻色-愛因斯坦凝聚體, 原子總數約為 1 05個, 全部處于 | 2,2〉 態.然后微波將所有原子絕熱轉移至|1,1〉態, 此時原子處于z方向的磁場中, 對應 | 1,1〉 和|1,0〉的塞曼能級分裂為22.305 MHz, 見圖4, 自此完成了原子的初始制備過程.為了研究單雙受激拉曼過程中拉曼光之間的相對相位是如何操控原子的拉曼耦合強度, 需要將實驗過程分為三步: 第一步, 沿著 x 方向輸出12 μs的 π /2 脈沖(紅失諧的Raman 1, 2), 其偏振相互垂直, 兩束光頻差與塞曼能級分裂相同, 最后利用自由飛行展開(time of flight, TOF)測量原子數, 通過調節光強, 讓原子經歷12 μs的 π /2 拉曼躍遷后, | 1,1〉 和 | 1,0〉 布居數各占50%; 第二步, 方法類似于第一步, 沿著 x 方向輸出12 μs的 π /2 脈沖(藍失諧的Raman 3, 4),其偏振相互垂直, 通過調節光強, 使其作用后原子在 | 1,1〉 和 | 1,0〉 布居數也各占50%; 第三步, 同時輸出12 μs的 π /2 脈沖(Raman 1, 2和3, 4), 通過調節Raman 1的相位, 利用TOF測量原子在|1,1〉和 | 1,0〉 的布居數比值, 觀察拉曼光之間的相對相位與拉曼耦合強度的對應關系.

4 實驗結果和分析

情況1單受激拉曼過程

只利用鈦寶石激光器1輸出一對 π /2 脈沖的拉曼光Raman 1, 2實現單受激拉曼過程, 見圖3, 通過改變Raman 1的射頻場的相位 φext測量原子在|1,0〉態的布居數分布, 見圖5, 可以看到一對拉曼光之間的相位差對拉曼躍遷沒有影響, 處于量子態|1,0〉的原子布居數始終為50%.

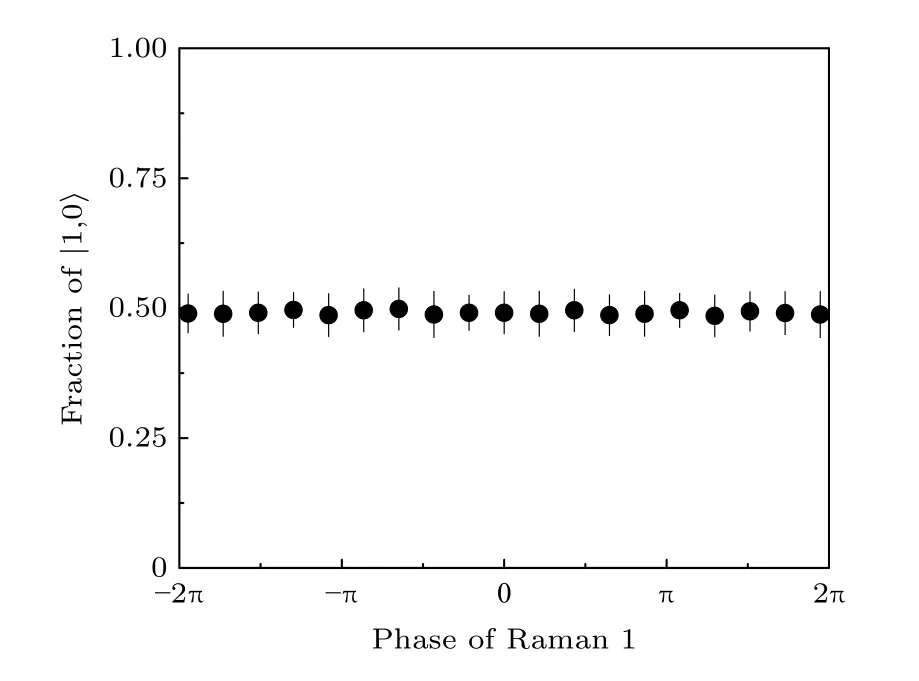
圖5 量子態 | 1,0〉 的布居數隨一對拉曼光之間的相位差的關系圖Fig.5.Measure the population in | 1,0〉 as a function of phase difference of two Raman lasers.

情況2雙受激拉曼過程

利用鈦寶石激光器1, 2分別輸出兩對拉曼光Raman 1, 2和3, 4, 見圖3, 其中鈦寶石激光器1輸出激光頻率為: fC=384.0000THz , 鈦寶石激光器2輸出激光頻率為: fS=384.2484THz , 通過相應的AOM移頻后, 便可以實現雙受激拉曼躍遷過程.在這種頻率狀態下, Raman 1, 2和3, 4之間的相對相位為為相對相位的初始相位差.通過改變相對相位 φext測得圖6的紅色實線(紅色虛線為理論擬合的結果, 得:=-0.157π), 圖中橫坐標為兩對拉曼光的相對相位(即: 射頻1的相位), 縱坐標為原子處于|1,0〉量子態占總量子態布居數的比例, 可以看出,通過改變兩對拉曼光的相對相位可以控制原子的受激拉曼耦合強度.

在 fS固定的情況下, 調節鈦寶石激光器1輸出激光頻率為: fC=383.7652THz , 在這種頻率狀態下, Raman 1, 2和3, 4之間的相對相位為Δφ=為相對相位的初始相位差.通過改變相對相位 φext測量得到圖6藍色實線(藍色虛線為改變初始相位后, 理論擬合的結果, 得:=-0.755π).該結果證明了通過改變兩對拉曼光的相對相位就可以實現對拉曼耦合強度的控制.進一步改變鈦寶石激光器1輸出激光頻率后,布居數曲線發生了平移, 該現象是由于改變鈦寶石激光器1輸出激光頻率導致引入額外的固定相移,主要來源為鈦寶石激光器1頻率的改變導致波矢k1,2發生改變, 從而改變一對拉曼激光的光程差.綜上可知: 當改變頻率 ωC時, 同時改變了激光的波矢和光程, 間接地改變了兩對拉曼光之間的相對相位, 因此布居數曲線發生了平移.

圖6 實驗測量量子態 | 1,0〉 的布居數隨兩對拉曼光間的相對相位的變化關系.紅色實線使用的鈦寶石激光器1, 2輸出頻率分別為: f C=384.0000THz , f S=384.2484THz ,紅色虛線為理論計算圖.藍色實線使用的鈦寶石激光器1, 2輸出頻率分別為: f C=383.7652THz , f S=384.2484THz ,藍色虛線為理論計算圖Fig.6.Measure the population in | 1,0〉 as a function of phase of four Raman lasers.The red solid line:fC=384.0000THz , f S=384.2484THz.The blue solid line: f C=383.7652THz , f S=384.2484THz.The red and blue dotted line is the theoretical diagram.

5 總 結

本文發展了一種利用兩對拉曼光間的相對相位精確控制拉曼耦合強度的新方法, 設計了穩定的拉曼激光的光路, 從而保證兩對拉曼光在傳輸過程中光程穩定.在此基礎上, 測量了兩個量子態的布居數隨兩對拉曼光之間的相對相位的變化關系.該方法為超冷原子量子模擬實驗提供了一個獨特的操控參量—激光相位, 希望未來能夠利用該技術對光與原子相互作用進行操控從而實現更為豐富的物理現象.