非接觸多磁環負剛度機構非線性剛度行為特性研究
王 瑤,李占龍,,劉 琪,連晉毅,王建梅,秦 園
(1.太原科技大學 機械工程學院,太原 030024;2.教育部重型機械工程研究中心,太原 030024)
Carrella等[2]提出的三彈簧結構首先為負剛度的研究打開了思路,利用兩斜置彈簧提供負剛度。Liu等[3]提出了歐拉屈曲梁結構作為負剛度來調整平衡位置時的動剛度。Valeev等[4]提出了單獨碟簧和環形結構組合而成的碟簧模型。任旭東等[5]采用兩個水平對稱空氣彈簧作為負剛度。徐道臨等[6]將5個線性彈簧并聯組合設計了非線性低頻隔振器。藍雙等[7]在新的結構設計中棄用了壓縮彈簧,采用拉伸彈簧的準零剛度隔振器。與前者對比后發現拉伸式具有更寬的準零剛度區間以及結構上的優勢。杜寧等[8]通過利用平行四邊形的不穩定性來產生負動剛度。Liu等[9]設計了凸輪-滾子-非線性彈簧機構,并討論了水平阻尼對系統隔離力激勵和位移激勵的能力的影響。張春輝等[10]通過在平衡位置設置一定的預緊力的準零剛度隔沖器來提高平衡位置附近的魯棒性。
近年來也陸續有學者利用磁的特殊性質構建負剛度元件。Zhou等[11]利用電磁鐵設計了剛度可調的具有高靜剛度-低動剛度的磁性隔振器。磁彈簧提供負剛度,磁彈簧由電磁鐵和永磁鐵構成,剛度值可以隨電流變化。Dong等[12]展開磁力準零剛度隔振技術研究,開發了由螺旋結合構成的高靜態低動態剛度的多維低頻隔振器。柴凱等[13-16]分別利用等效磁荷法建立矩形永磁鐵和雙環形永磁鐵的磁力和剛度解析模型。嚴博等[17]提出利用多個永磁體的不同磁化方式和布置形式來實現高性能的非線性隔振,驗證了在小幅值和大幅值激勵下的有效隔振。Yang等[18]基于幾何非線性動力學負剛度特征衍生的幾何非線性隔振理論,建立了超低頻時滯隔振器控制策略,實現對小于1 Hz振動的有效控制。蘇智偉等[19]比較分析了含負剛度動力吸振隔振系統的傳遞和響應特性。Kim等[20]將準零剛度隔振器應用于超精密測量傳感器,實現對低頻微幅振動的有效控制,大幅提高傳感器精度。
本文基于磁彈簧原理,提出一種非接觸多磁環負剛度機構(non-contact negative stiffness, NCNS),結合氣動人工肌肉(pneumatic artificial muscle, PAM)正剛度機構,設計了一種非接觸準零剛度隔振系統。為探明隔振系統剛度機理與特性,以負剛度機構為研究對象,搭建了負剛度實驗臺,從理論和實驗對其剛度行為特性開展了系統研究,為隔振系統動力學建模、參數優化及其工程應用提供理論基礎。
1 非接觸多磁環負剛度機構
圖1為非接觸多磁環準零剛度隔振器結構,主要包括承載平臺、PAM正剛度機構和NCNS負剛度機構。承載平臺由球鉸與中心軸連接,可有效適應偏載工況;正剛度機構由PAM多自由度平臺構成,可根據載荷情況實時調節正剛度大小及平臺角度,達到對準零剛度系統內部傳力的垂向歸一化,進而實現內部解耦,以適應承載剛度和平衡剛度需求;NCNS負剛度機構由同軸排列的上磁環、下磁環和內磁環組成,上下磁環固定在內殼體凹槽處,內磁環固定在中心軸上,與上下磁環呈相吸磁極分布。振動通過球鉸平臺傳遞給中心軸,中心軸帶動內磁環在上下磁環之間運動,由于磁力作用產生負剛度。
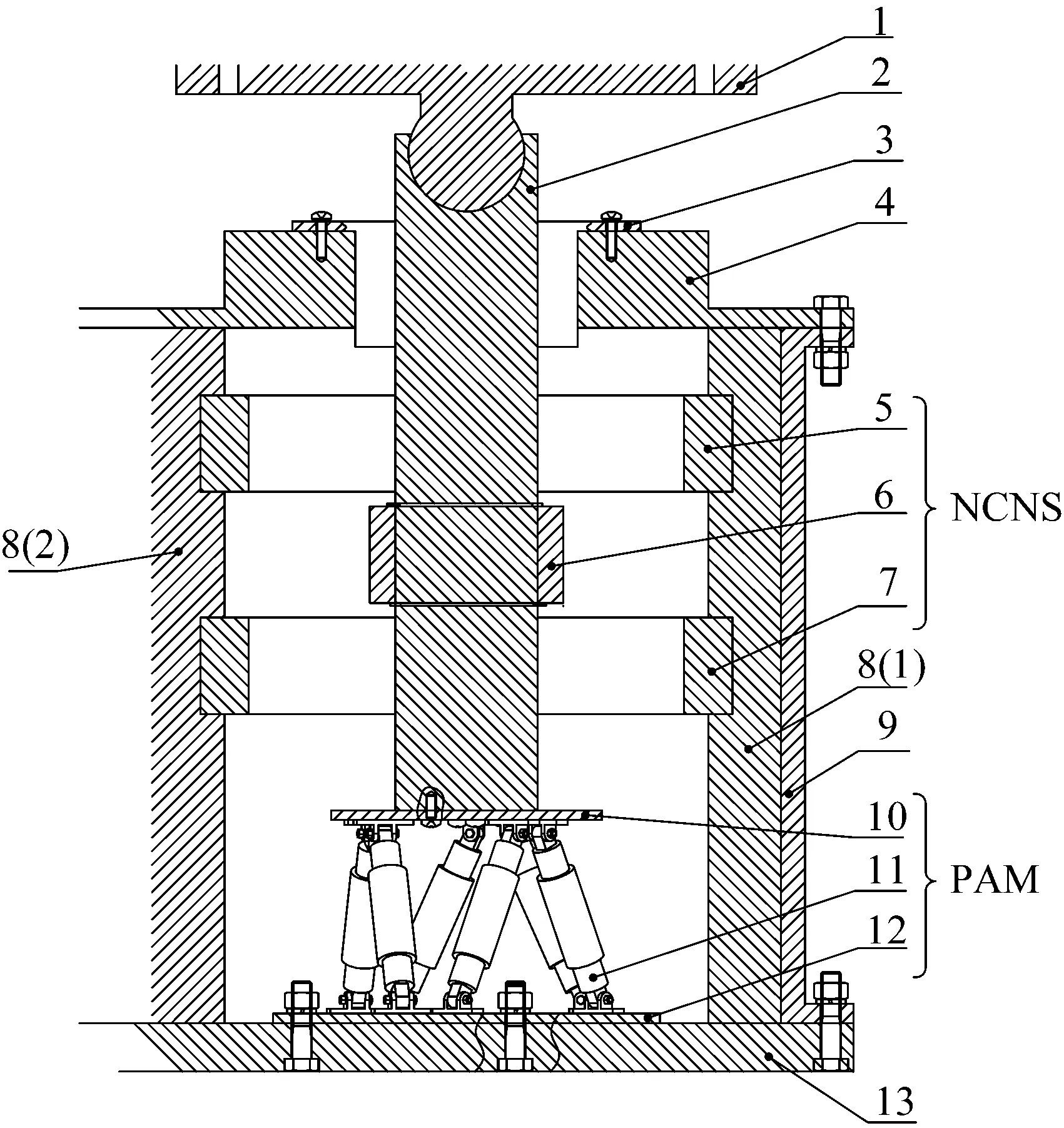
1.球鉸承載平臺; 2.中心軸; 3.直線軸承; 4.上端蓋; 5.上磁環; 6.內磁環; 7.下磁環; 8(1).內殼體1; 8(2).內殼體2; 9.外殼體; 10.PAM上蓋; 11.PAM; 12.PAM座; 13.底座。
為探明負剛度機理與特性,將負剛度機構作為研究對象,并做如下假設:① 內磁環與上下磁環沿軸向等距設置;② 上下磁環幾何參數相同,且與內磁環呈相吸磁分布;③ 內磁環重力遠小于作用磁力,可忽略;④ 考慮內外(上下)磁環因相對位移而產生對內磁環的綜合垂向力,將負剛度機構等效為圖2所示的坐標系。
如圖2所示,將坐標系xoy面與內磁環下表面中心點重合,內磁環垂向運動為z軸,且向上為正。內磁環與上下磁環沿軸向等距設置,距離為l;上下磁環間距離為H;內磁環的內徑、外徑和高度分別為d1、D1、T1,上下磁環的內徑、外徑和高度分別為d2、D2、T2,z為內磁環沿軸向移動的位移;下角標1表示內磁環變量,下角標2表示上下磁環變量,下角標2a指代上磁環變量,下角標2b指代下磁環變量。
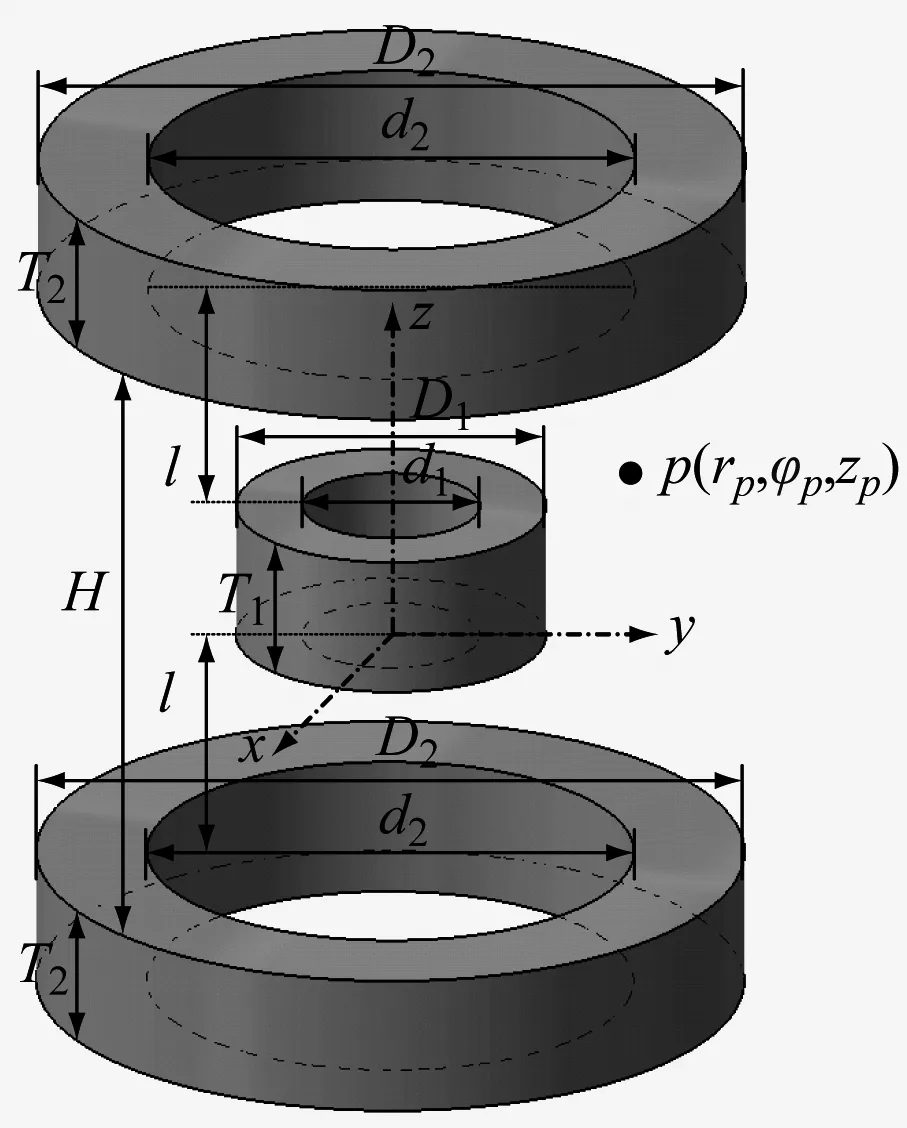
圖2 負剛度機構坐標系
2 負剛度理論建模
2.1 三磁環模型磁力計算
由分子電流假說[21]永磁體的磁矩可表示成由體電流密度Jt和面電流密度Jm構成,故由磁媒質中的安培定律得到體電流密度和面電流密度的表達式為
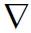
(1)
Jm=M×e
(2)
式中:e為垂直磁體表面的單位矢量;M是沿軸向的磁化強度矢量。環形永磁鐵沿軸向均勻磁化,磁環強度矢量分別為M1和M2;磁化強度矢量與剩余磁通密度Br1和Br2的關系分別為M1=Br1/μ0,M2=Br2/μ0,μ0=4π×10-7NA-2為真空磁導率。
由于沿軸向均勻磁化,根據式(1)、(2)可知,三磁環內環形永磁體的體電流密度均為零,只在環形永磁體的內外圓柱表面具有非零的面電流密度,表示為
(3)
式中:φ為內外圓柱表面切向單位向量。
在圖2所建坐標系空間內取點p(rp,φp,zp),根據比奧-薩伐爾定律[22]可知,p點沿軸向磁化的環形永磁體產生的剩余磁通密度表示為
B(rp,φp,zp)=Br(rp,φp,zp)r+
Bφ(rp,φp,zp)φ+Bz(rp,φp,zp)z
(4)
其中,
(5)
rpcos(φp-φ1)]Φ0r(i)dφ1dz1
(6)
Bφ(rp,φp,zp)=0
(7)
(zp-z(k))2|1/2
(8)
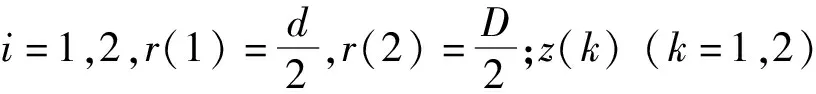
內磁環承受的總磁力Fz由上磁環對其吸引力F1-2a和下磁環對其吸引力F1-2b疊加,表達式為
Fz=F1-2a+F1-2b
(9)
由安培定律可知,內磁環內外圓柱表面上的電流元Idl在上下環形永磁體產生的磁場中受到的安培力為:
dF=Idl×B
(10)
故
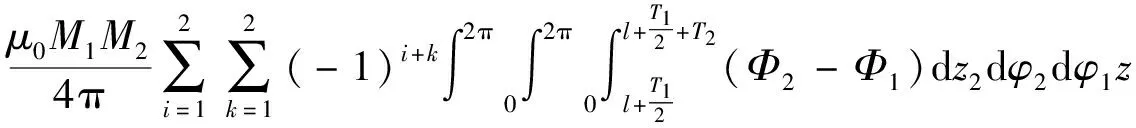
(11)

(12)
式中:

(13)

(14)
(15)
2.2 非線性負剛度
將內磁環軸向磁力對z(k)求一階偏導數,即可得負剛度機構非線性剛度解析表達式為

Φ3)dz2dφ2dφ1
(16)
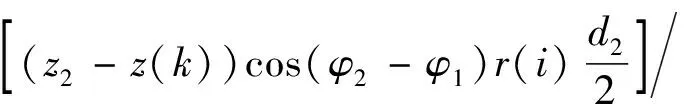
(17)
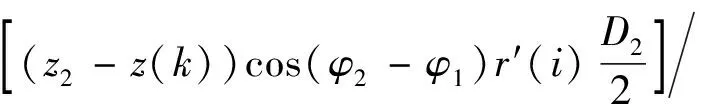
(18)
(19)
3 模型驗證
3.1 模型建立
基于表1所列參數建立負剛度機構計算模型,進行磁場耦合特性分析,并獲得負剛度行為特性。在ANSYS Maxwell中建立多磁環負剛度模型,按照表1設置磁環參數并設定z向充磁,得到有限元仿真模型。圖3和圖4分別為軸向充磁條件下磁通密度分布圖和磁場強度分布圖。由圖3和圖4可知,任一磁環的磁場強度都沿軸向區域分布,且徑向對稱,與充磁方向一致;磁環上下端面磁性最強,可實現相鄰磁面的最大磁力且均勻分布;端面磁場強度峰值為6.145×105A/m。

圖4 磁場強度分布圖

表1 環形永磁體的參數
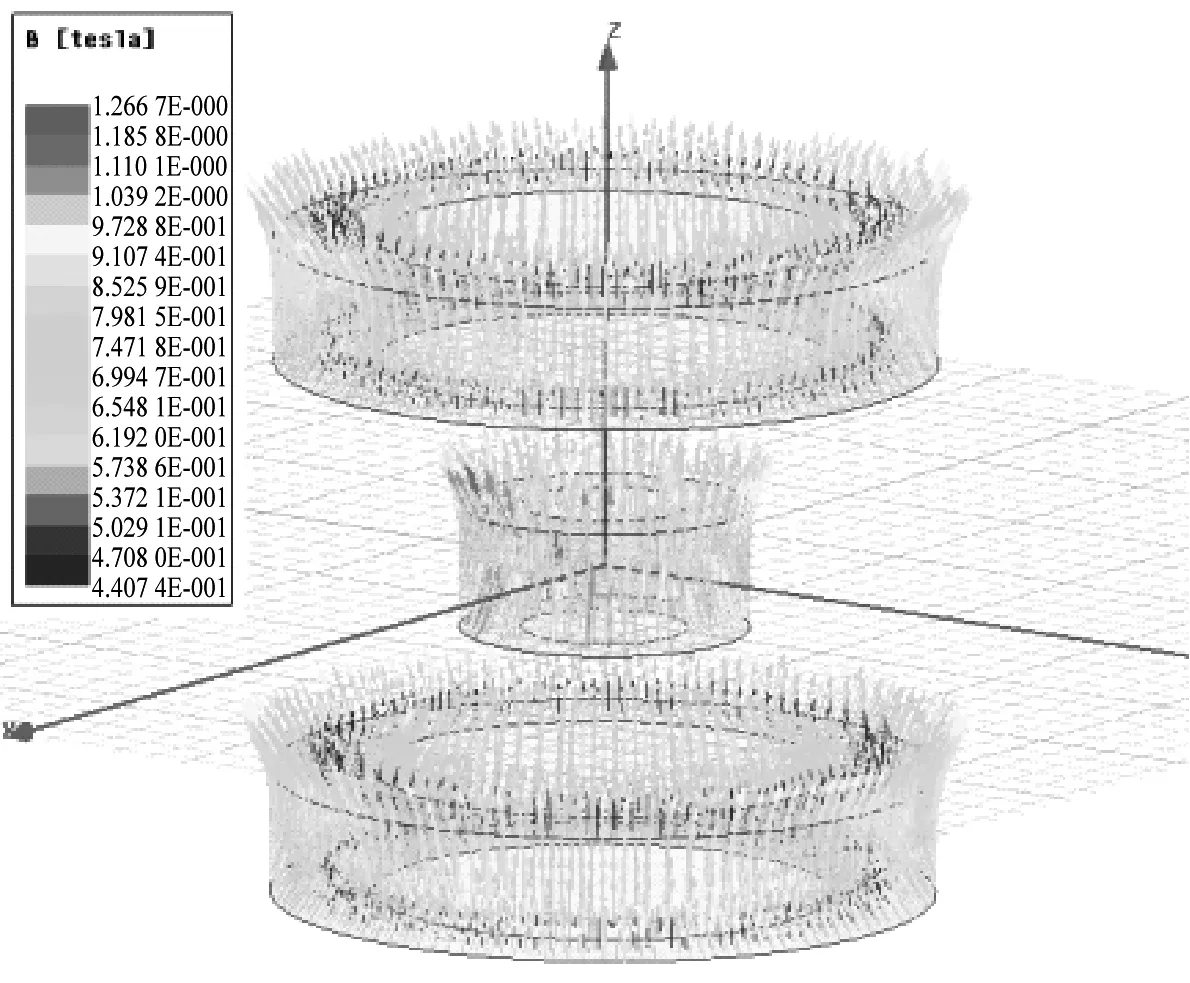
圖3 磁通密度分布圖
3.2 實驗驗證
圖5為搭建的負剛度實驗臺。實驗臺上安裝有刻度軸、高精度動態測力計、磁環夾具和負剛度磁環(釹鐵硼)等。上下磁環固定在刻度軸上,測力計與內磁環同軸連接,可沿刻度軸上下移動,實現對不同位移下內磁環的復合軸向磁力進行測試并記錄。實驗前首先測得中心軸及內磁環整體重力為1 N,對于磁環間磁力而言可忽略不計,與計算環境條件統一。

1.測力計固定座;2.固定軸;3.下磁環;4.底座;5.梅花手擰螺絲;6.內磁環;7.磁環固定座;8.上磁環;9.測力計。
依據表1所示參數,設置實驗條件,獲得在H=50 mm且軸向最大位移z為±20 mm下的內磁環力-位移數據,對比結果見圖6。從圖6中可以發現,計算結果與實驗數據基本吻合,二者校正決定系數Adjusted R-square為0.999 75,驗證了計算模型的可靠性。
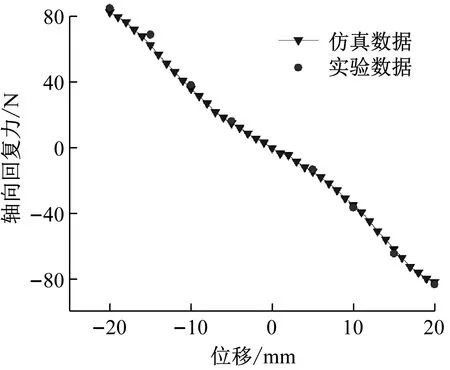
圖6 擬合仿真曲線和實驗數據
4 負剛度行為特性
由式(16)可知,負剛度Kz由磁環幾何尺寸D、d、T、H和l以及永磁體的物理特性決定。因此,對于給定的釹鐵硼環形永磁體負剛度機構,可通過調節其幾何和物理參數來探究參數特性,揭示負剛度行為規律。
4.1 充磁方向
分別計算沿Z向充磁和沿Y向充磁條件下負剛度行為特性,見圖7。由圖7可知,在同樣磁場強度條件下,兩種充磁方向的負剛度區間寬度相同,但沿Z向充磁負剛度機構的最大彈性力大于沿Y向充磁負剛度機構,差值約50 N。因此,沿Z向充磁負剛度機構具有較強的負剛度特性,承載能力顯著。
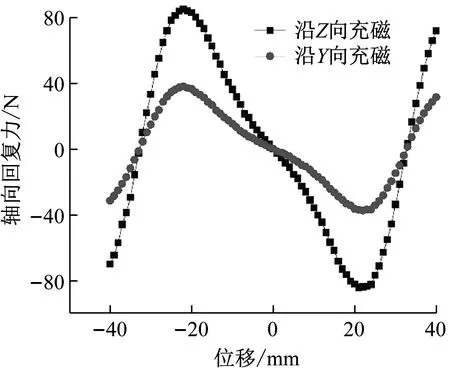
圖7 磁方向對負剛度的影響
4.2 幾何參數
圖8~11分別為改變磁環的內徑d、外徑D和厚度T,以及上下磁環間距H得到的負剛度機構力-位移曲線。首先可以發現,磁環內、外徑和厚度的變化僅會影響負剛度機構的最大彈性力,對負剛度區間寬度影響較小,基本穩定在±20 mm之間。在負剛度位移區間,負剛度特性對內磁環外徑和上下磁環內徑的敏感性較強,即較小內磁環外徑/外磁環內徑變化會導致負剛度特性的大幅變化;磁環內徑的增大、外徑較小或厚度減小均會導致負剛度特性減弱,這是由于幾何參數的變化會導致磁環體積的變化,進而導致磁場強度的變化。因此,在準零剛度隔振器設計時,可通過改變磁環內外徑和厚度的變化,在不改變負剛度區間的基礎上,來調節隔振器的承載剛度,進而確定與之匹配的正剛度范圍。由圖11可知,隨H增加,負剛度區間從-15~15 mm擴展到-25~25 mm附近,但負剛度峰值穩定不變。因此,可以通過調節H在不改變負剛度行為特性的基礎,擴展隔振系統的行程。
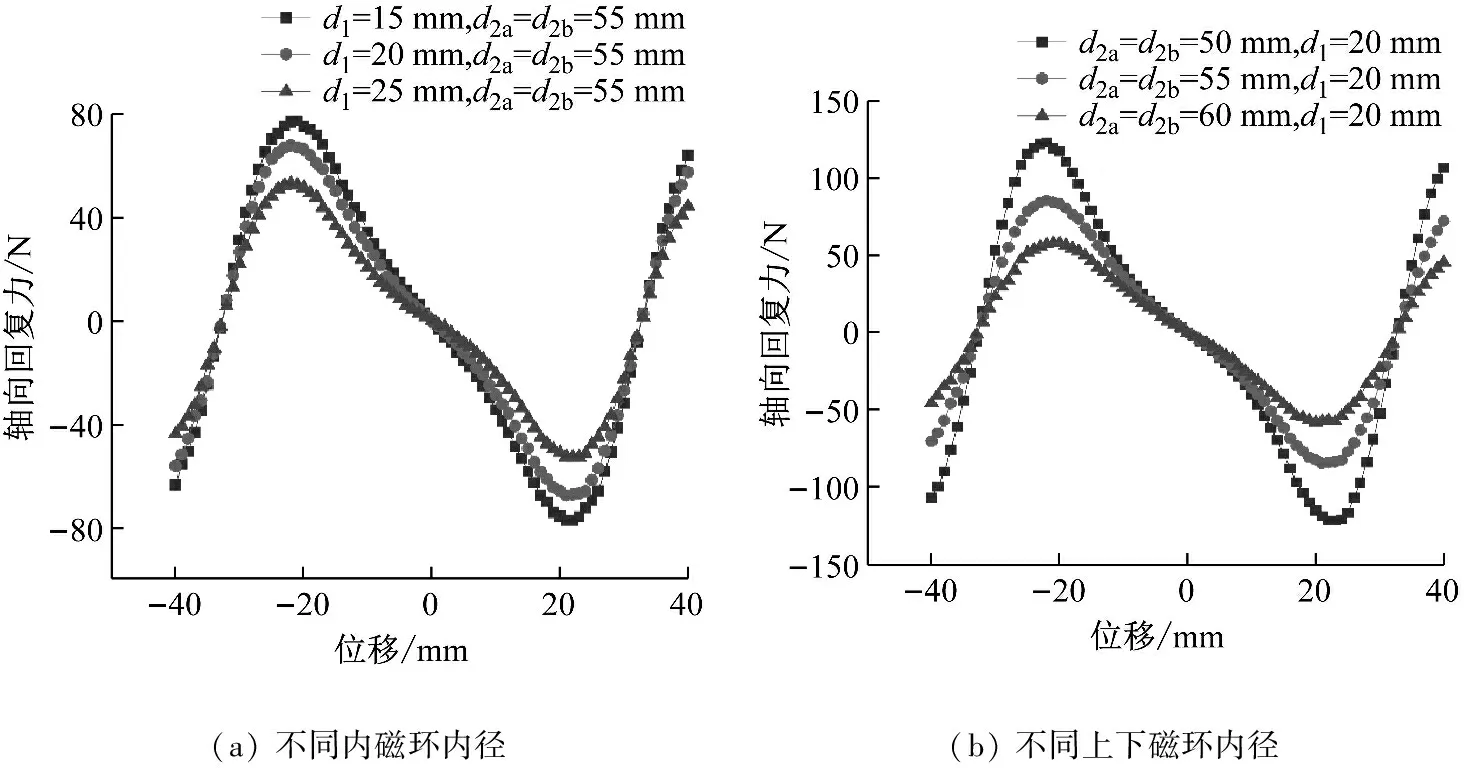
圖8 環形永磁體內徑對磁剛度的影響
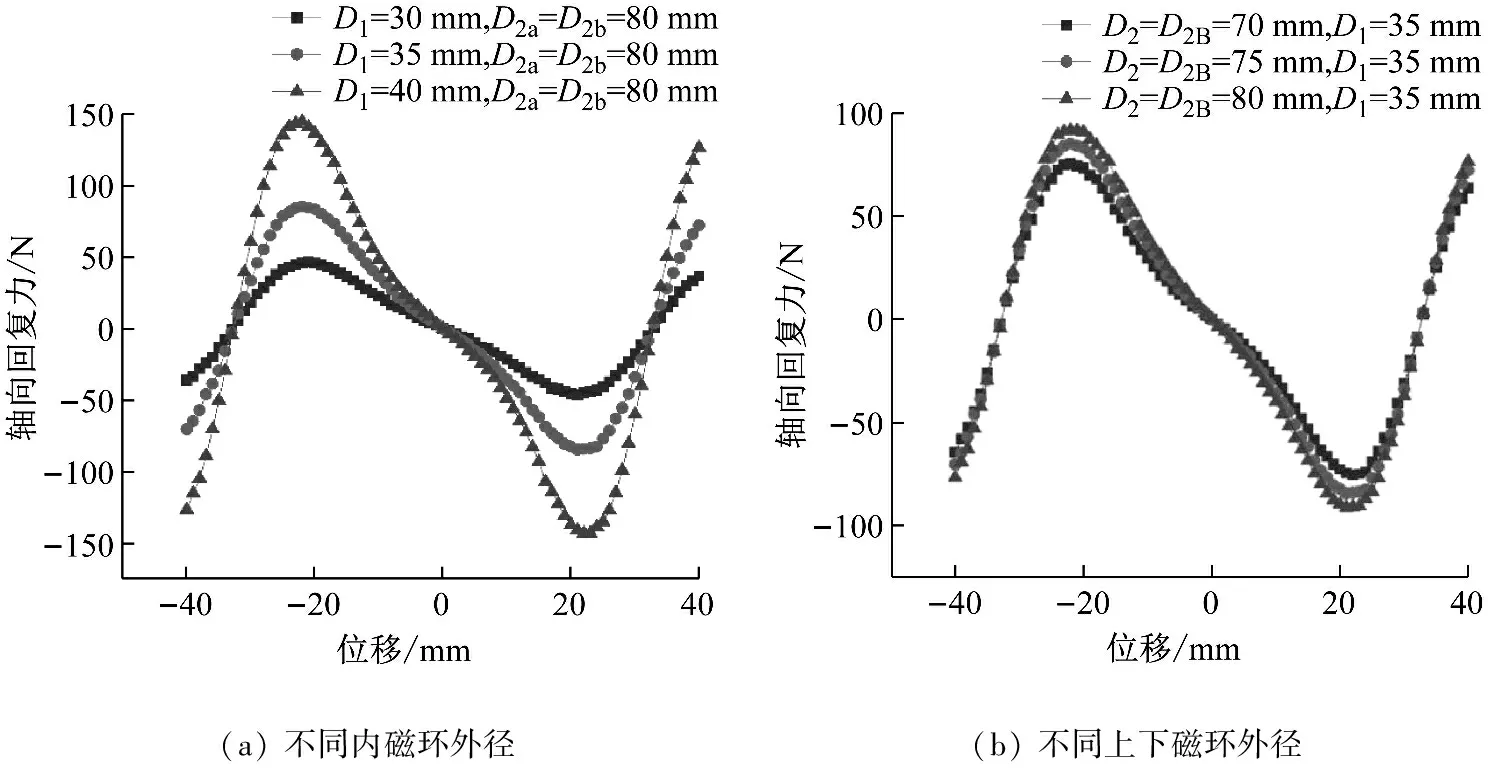
圖9 環形永磁體外徑對磁剛度的影響
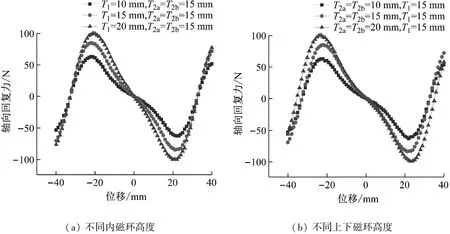
圖10 磁環高度T對磁剛度的影響
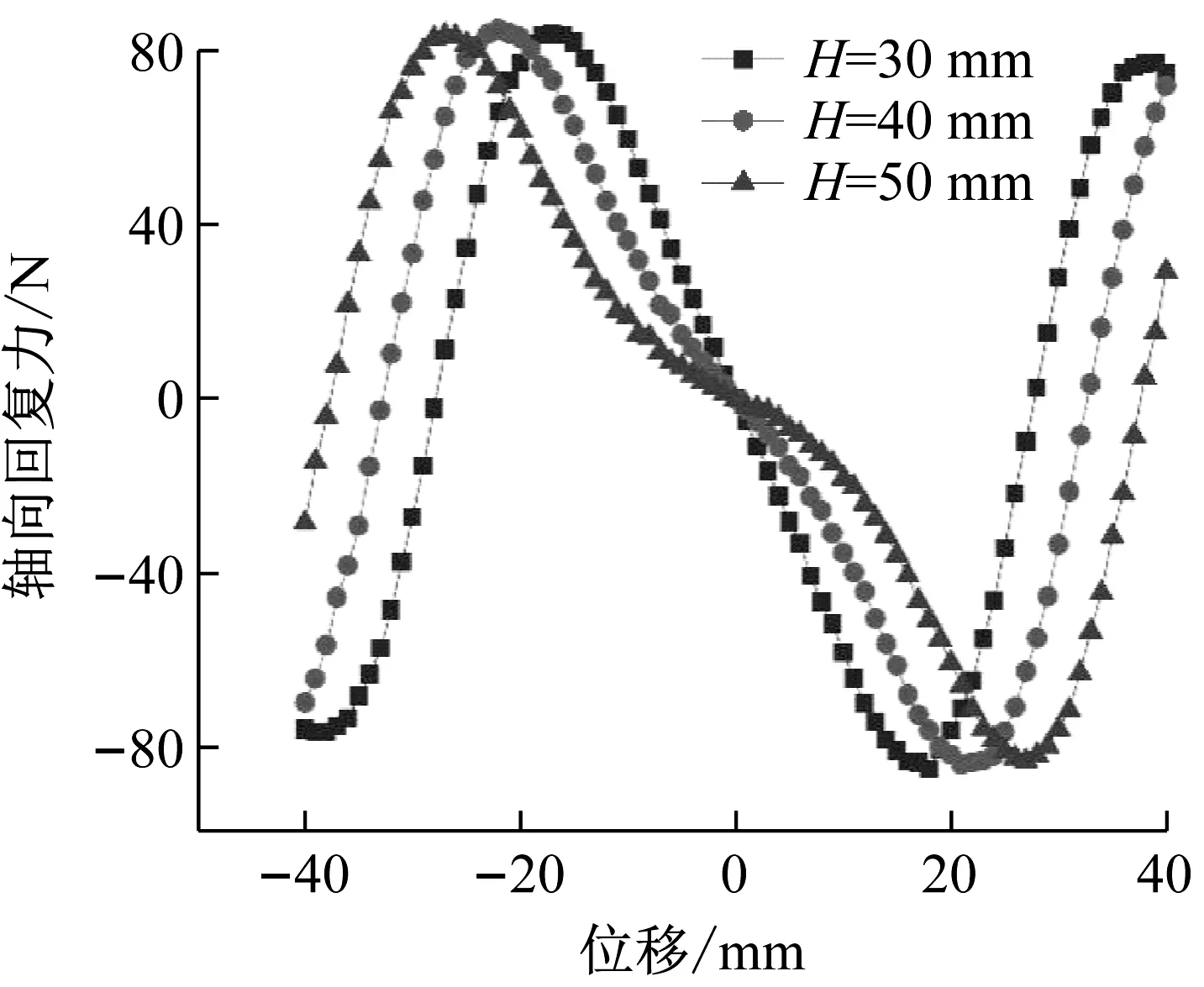
圖11 上下磁環距離H對磁剛度的影響
4.3 磁場強度
圖12為不同磁導率Br值下負剛度機構的力-位移曲線。由圖12可以發現,磁導率Br的增加,負剛度機構的最大彈性力增大,其負剛度區間保持不變,與解析剛度式(16)一致。
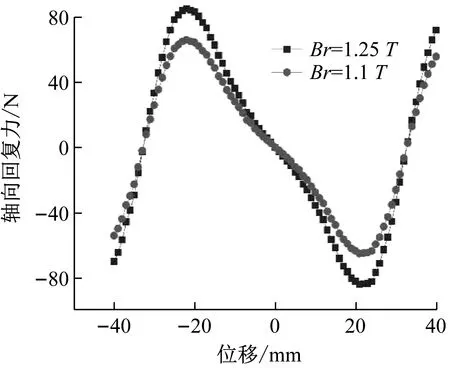
圖12 不同Br值對磁剛度的影響
5 結 論
本文提出了一種新型非接觸多磁環準零剛度隔振器,由三磁環NCNS負剛度機構和PAM正剛度機構串聯組成。為探明隔振系統負剛度機理與特性,將NCNS負剛度機構作為研究對象,推導出其解析剛度表達式,建立了計算模型,對其負剛度行為特性及參數特性開展了系統研究。主要結論有:
(1)NCNS負剛度機構具有顯著的負剛度特性,在同樣幾何參數和負剛度區間條件下,軸向充磁比徑向充磁獲得更大的負剛度,配合與之匹配的正剛度機構,在滿足低頻寬帶隔振性能的基礎,能獲得較強的承載能力。
(2)負剛度機構剛度行為特性具有明顯的參數依賴性,調整磁環參數D、d、T和Br值可提升負剛度的承載性能,但不改變負剛度區間;調整H可拓展負剛度區間,但不改變承載性能。
(3)計算模型與實驗有很好的一致性,驗證了該模型的正確性,為下一步新型準零剛度隔振系統動力學建模、參數優化及其工程應用提供了理論基礎。

