基于改進蝙蝠算法優化廣義回歸神經網絡的巖質邊坡穩定性預測
楊雅萍, 張文蓮, 孫曉云
(石家莊鐵道大學電氣與電子工程學院, 石家莊 050043)
巖土工程中,邊坡穩定性預測是一個重要的領域。邊坡是一個動態開放和非線性的復雜系統,目前研究表明邊坡滑動的誘發因子之間具有不確定性、離散性、隨機性以及相互之間復雜的關聯作用[1]。在邊坡穩定性確定性分析法中,極限平衡法和傳統的數值分析方法無法準確描述邊坡的非線性特征。近年來人工神經網絡的發展,及其非線性動態處理的優勢,神經網絡也被逐漸應用到邊坡工程實際中來預測邊坡穩定性。李龍等[2]在傳統反向傳播(back propagation,BP)神經網絡中引入附加動量、自適應學習速率和模擬退火算法,提出了改進的BP神經網絡,對網絡收斂速度慢和易陷入局部最小值的問題有較好的改進等。牛鵬飛等[3]引入核主成分算法(principal component analysis,KPCA)和Levenberg-Marquardt(L-M)算法建立了主成分分析(principal components analysis, PCA)-LMBP邊坡穩定性網絡預測模型。臧焜巖等[4]在傳統BP神經網絡中引入遺傳算法(genetic algorithm,GA),用來更新網絡的權值和閾值,建立了GA-BP邊坡穩定性預測模型。
以上3種神經網絡模型輸入均采用Mohr-coulomb(M-C)準則中的內聚力、內摩擦角等巖土力學參數。雖然目前大多數學者均采用M-C準則中的力學參數,但M-C準則無法解釋巖質邊坡的非線性變形破壞現象。改進Hoek-Brown(H-B)準則對巖體固有的非線性破壞特點可以很好地反映,而且該準則已在巖體強度預測及計算領域得到廣泛應用[5]。目前,BP神經網絡隱含層神經單元數目在實際應用中不存在一個合理的解析式,仍是以經驗公式確定,而BP神經網絡在工程應用成敗的關鍵是其網絡的構造[6]。對于網絡的構造,廣義回歸神經網絡(generalized regression neural network,GRNN)網絡結構與輸入樣本維數和數量有關,網絡結構無需根據經驗設定。
針對上述兩個問題,提出了一種邊坡穩定性預測新方法,即基于廣義H-B準則的巖體力學參數,采用交叉變異優化的蝙蝠算法,構建了改進的BA-GRNN神經網絡模型,對邊坡的穩定性和安全性進行預測。
1 算法原理
1.1 廣義Hoek-Brown準則
在統計分析大量巖體原位試驗成果后,得到了反映巖體產生破壞的半經驗準則Hoek-Brown強度準則,該準則主要反映了巖體最大和最小主應力的關系[7],可表示為

(1)
式(1)中:σ1、σ3分別為最大、最小主應力;σci為完整巖石材料單軸抗壓強度;mb、s、a為反映巖體特征的經驗參數,可以由巖體地質強指標、巖體的擾動因子和完整巖石經驗常數計算確定。
1.2 廣義回歸神經網絡
廣義回歸神經網絡結構以徑向基神經網絡為基礎,具有很強的非線性映射能力和學習速度[8]。
GRNN網絡結構有4層,其中輸入變量由輸入層直接傳遞給模式層,傳遞函數為
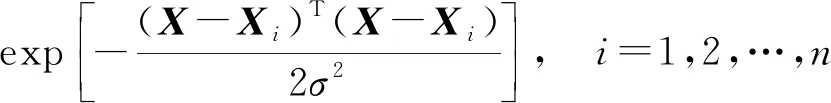
(2)
式(2)中:X=[x1,x2,…,xn]為輸入學習樣本;Xi為訓練樣本;pi為指數分子為學習樣本X與訓練樣本的Xi的歐氏距離平方和;徑向基函數為高斯函數,σ為高斯函數標準差,隱含層位置中基函數的形狀由σ決定。
輸出層輸出樣本為Y=[y1,y2,…,yn],輸出層神經元輸出為

(3)
式(3)中:Pi為每個模式層神經元的輸出;SNj、SD分別為求和層來兩類神經元的求和結果;yij為Yi的第j個元素。
由式(1)可知,σ為GRNN網絡需要優化的唯一參數,σ的取值會影響網絡預測結果,合理的σ取值,可以增強GRNN網絡的泛化性,σ的較大取值,使得網絡預測值與所有樣本因變量的均值近似相等,預測效果不好;反之當σ取值趨于0,預測值則會更加準確[8]。
GRNN具有柔性網絡結構、高度容錯性及魯棒性[9],針對樣本少和部分樣本數據精準度比較差的問題,能得到較好的預測效果。
1.3 蝙蝠算法
蝙蝠算法類似于粒子群算法,不同的是蝙蝠算法增加了頻率和響度因素,通過頻率變化影響蝙蝠速度,從而改變蝙蝠位置對蝙蝠個體進行尋優。目前蝙蝠算法已成為搜索全局最優解的有效方法[10]。算法具體闡述如下:隨機初始化虛擬蝙蝠的飛行速度vi、位置xi,脈沖頻率fi、脈沖響度Ai和脈沖率r,蝙蝠發現獵物時,改變頻率、減小響度和增加脈沖發射率來更新蝙蝠個體速度和位置,通過適應度函數評價當前個體位置的優劣,對個體進行優勝劣汰,選擇最優解。
對進化過程中蝙蝠種群t時刻的搜索脈沖頻率fi、速度vi和位置xi進行更新,分別表示為
fi=fmin+(fmax-fmin)β
(4)

(5)
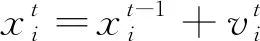
(6)
式中:β∈[0,1]為均勻分布的隨機數;X*為當前所有蝙蝠的最優解;蝙蝠的初始搜索脈沖頻率fi在[fmin,fmax]內隨機確定。
對t時刻脈沖音量Ai和脈沖發射率ri進行更新,可表示為
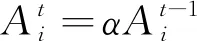
(7)
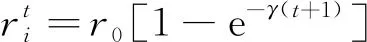
(8)
式中:搜索脈沖頻率范圍為[fmin,fmax];音量的衰減系數數為α;最大脈沖音量為A0;最大脈沖率r0;搜索頻率的增強系數為γ。
合理的音量衰減系數和搜索頻率可以有效平衡算法尋優精度和收斂速度,在算法仿真中需要不斷調整音量衰減系數和搜索頻率。與其他粒子群算法相比,模型簡單,參數較少,收斂速度快已成為蝙蝠算法的突出優點。
在算法尋優過程中,由于蝙蝠種群個體缺乏變異機制,超級蝙蝠對種群中其他蝙蝠的吸引會使得種群多樣性顯著下降[11]。采用交叉變異算子來豐富蝙蝠種群的多樣性。
2 建立改進BA-GRNN網絡模型
2.1 輸入輸出變量的確定
研究影響邊坡穩定性的因素分為邊坡巖土力學參數和邊坡幾何形態兩方面。對于巖土力學參數的影響,基于廣義Hoek-Brown經驗準則[12-17],采用巖體重度rG、地質強度指標GSI、擾動因子D、單軸抗壓強度σci、巖體軟硬程度參數mi表征,對于邊坡幾何形態的影響,采用坡高H,坡角αs表征,將以上7個因素作為BA-GRNN網絡模型的輸入,輸出為邊坡安全系數和邊坡狀態[18-23]。搜集120個經典實例作為邊坡樣本[24-28],最后10個作為預測樣本。對于網絡不同的輸入參數,其數值上相差很大,訓練前對輸入數據進行歸一化處理可以提升網絡收斂速度,最后對預測結果網絡輸出安全系數和邊坡狀態進行反歸一化處理,得到與實際值相同量綱的值。
2.2 改進BA-GRNN模型建立
采用廣義H-B準則中的巖體力學參數,采用交叉變異算子改進的BA算法優化的GRNN神經網絡的光滑因子,建立改進BA-GRNN網絡,對邊坡的穩定性和安全性進行預測,改進后網絡拓撲結構如圖1所示。

圖1 BA-GRNN網絡拓撲圖
輸入層的7個神經元分別對應于2.1節中的7個影響因素,模式層神經元數目對應于2.1節中的110組訓練樣本。在增加蝙蝠種群多樣性方面,分別采用最常用和最基本的單點交叉算子和基本位變異算子來優化蝙蝠算法。單點交叉(one-point crossover)算子是指在個體兩兩配對的父代染色體編碼串中隨機設置交叉點A,然后在A處相互交換兩個父代的Ⅱ段染色體,交叉運算過程如圖2所示。
由圖2知,相互配對的父代染色體每一次交叉運算產生數量相同的子代染色體,而且根據交叉點選取的不同,兩個子代染色體來自兩個父代染色體基因座長度不同。

圖2 交叉算子示意圖
基本位變異(simple mutation)算子是對個體編碼基因座上的每一位隨機生成[0,1]內的隨機數r′,依變異概率pm與r′的大小,判斷該位是否進行變異運算,對判斷pm>r′的基因座上的基因值作為變異運算。變異過程如圖3所示。

圖3 變異算子示意圖
改進BA-GRNN神經網絡算法基本實現步驟如下。
步驟1學習樣本和預測樣本數據歸一化,輸入到改進后的網絡。
步驟2用二分法確定光滑因子初始取值范圍[a,b]。
步驟3初始化蝙蝠算法參數A0、r0、α、γ和最大迭代次數Nmax;[a,b]內初始化蝙蝠種群;初始化交叉概率pc和變異概率pm。
步驟4計算初始化種群適應度,記錄初始最優解適應度函數值fmin和其位置I,將位置I下的蝙蝠個體值賦給Best。
步驟5選擇新群體進行兩兩配對,根據交叉概率pc在相互配對的個體交叉點A點處相互交換父代個體的部分染色體,產生與父代數量相同的子代染色體。
步驟6對個體的每個基因座,根據變異概率pm對判斷為變異位的基因值做取反運算,如原基因值為0的取為1,反之原基因值為0的取為1,以此產生新的子代個體。
步驟7按式(3)~式(5)更新上述產生的個體的位置和速度。
步驟8若生成的均勻分布隨機數Rrand>r′,則給當前最優解一個隨機擾動,并在擾動后對新解進行越界處理,即對于超出給定范圍的值將其限制在邊界值上。
步驟9若生成均勻分布隨機Rrand>Ai,且適應度函數f(xi)>f(x*),則接受式(8)產生的解, 然后按式(6)、式(7)更新種群的響度和脈沖發射率。
步驟10計算所有蝙蝠個體的適應度值并對其進行排序,找到的適應度值最小值對應的個體即為當前最優解,同時記錄最優解對應的位置。
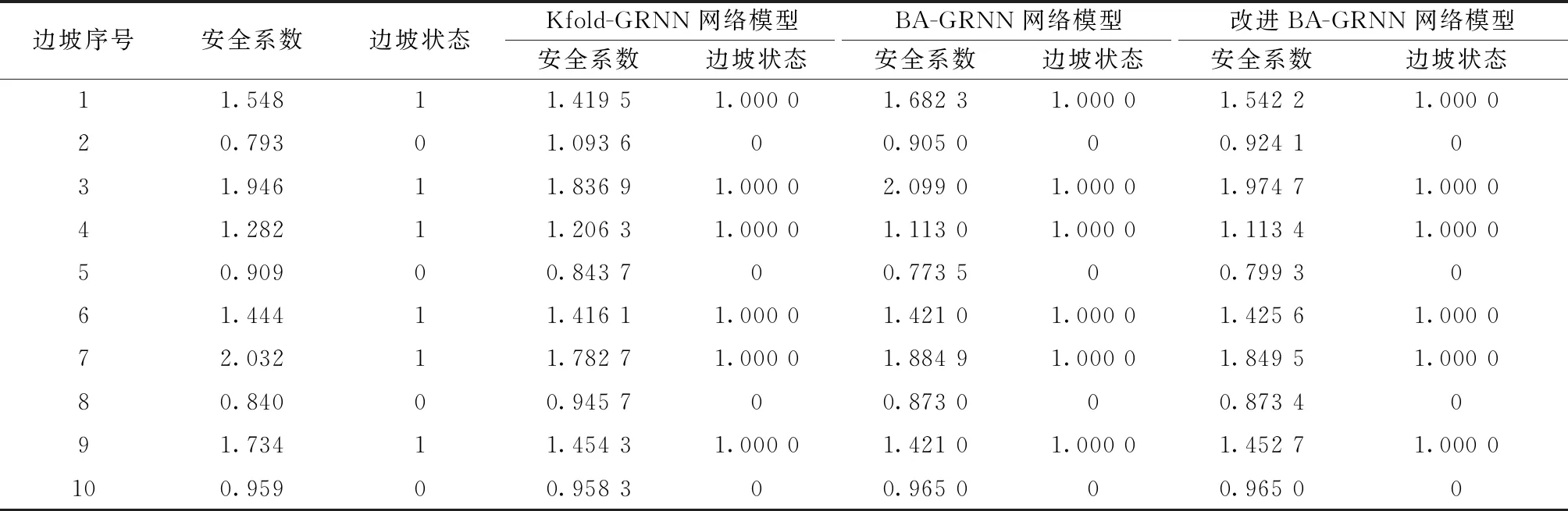
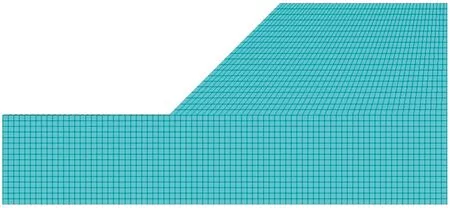
步驟11若上一步中產生的局部最優解適應度Fnew 步驟12重復步驟(4)~步驟(8)直至滿足設定條件,本文采用達到最大迭代次數作為算法結束的標志。 步驟13輸出全局最優解Best和最優解位置。 步驟14上一步輸出的最優解即為GRNN網絡的光滑因子,將10組預測樣本輸入到優化好的網絡,即可輸出預測結果。 改進BA-GRNN網絡算法流程圖如圖4所示。 圖4 改進BA-GRNN網絡算法流程圖 基于MATLAB2020平臺,網絡對所選110組樣本進行訓練后,在迭代300次后能得到較好預測結果。改進BA算法的初始化參數取值如表1所示。蝙蝠算法最優個體值為0.178,最優個體適應度函數值為1.207 4×10-3。圖5為適應度函數值的變化曲線。 終止代數=300 表1 改進BA算法初始參數 GRNN網絡光滑因子σ取值為0.178。為了進一步分析改進后BA-GRNN網絡的預測效果,與BA-GRNN神經網絡和K-交叉驗證選取GRNN光滑因子網絡(Kfold-GRNN)兩種模型預測結果進行比較,表2對比了3種網絡預測結果。 由表2可知,3種網絡對邊坡狀態預測結果完全相同。由圖6可以看出,對于邊坡安全系數的預測,改進后的BA-GRNN網絡模型對安全系數真實值的擬合效果更好。由3種網絡邊坡安全系數預測值得平均絕對百分比誤差(mean absolute percentage error,MAPE)和均方誤差(mean square error,MSE),如表3所示,進一步得到改進后的BA-GRNN網絡MAPE和MSE均小于前兩種網絡。由上述知,改進BA-GRNN網絡對邊坡穩定性的預測效果較好。 表2 3種網絡模型預測結果對比 圖6 安全系數對比 表3 3種網絡模型預測結果及誤差對比 選用經典邊坡算例,該邊坡為天然均質邊坡,邊坡巖體強度參數及幾何參數如表4所示。將邊坡算例在FLAC3D中進行建模,模型只考慮重力作用,底部邊界為固定約束,水平約束施加于兩側邊界,坡面設為自由邊界[29-31],由此所建模型如圖7所示。 表4 邊坡巖體強度參數及幾何參數 針對圖7模型,利用FLAC3D中model factor-of-safety命令計算邊坡安全系數,得安全系數為1.15,通過邊坡計臨界破壞狀態的最大剪應變云圖可得邊坡臨界破壞面,如圖8所示。 圖7 邊坡有限元模型 圖8 邊坡臨界破壞最大剪應變云圖 通過本文網絡對經典算例計算,得到安全系數和邊坡狀態的值為1.158 0和1.000 0,通過與FLAC3D的計算結果進行對比,可得本文方法與FLAC3D建模計算結果相近,網絡預測安全系數MAPE為0.70%。可見對于實際邊坡案例,改進后的BA-GRNN網絡對安全系數和狀態的預測是準確的。 (1)結合廣義Hoek-Brown準則,將Hoek-Brown準則所涉及的巖體參數作為穩定性影響因素,對巖質邊坡進行穩定性預測。分析結果顯示,所選擇影響因素對巖質邊坡有更好的適用性。 (2)利用改進的BA算法優化的GRNN網絡對邊坡的安全系數和狀態進行預測,通過與BA-GRNN和Kfold-GRNN神經網絡邊坡預測模型對比,改進BA-GRNN網絡安全系數的平均絕對百分比誤差在8%以下,均方誤差只有0.17%,而且對實際邊坡的安全系數和是否失穩可以進行準確的判斷。 (3)在邊坡穩定性的確定分析中,傳統的數值分析法不僅計算煩瑣,計算量大,時間長,而且對經驗的依賴性較強,所使用的方法可以很好地解決這些問題。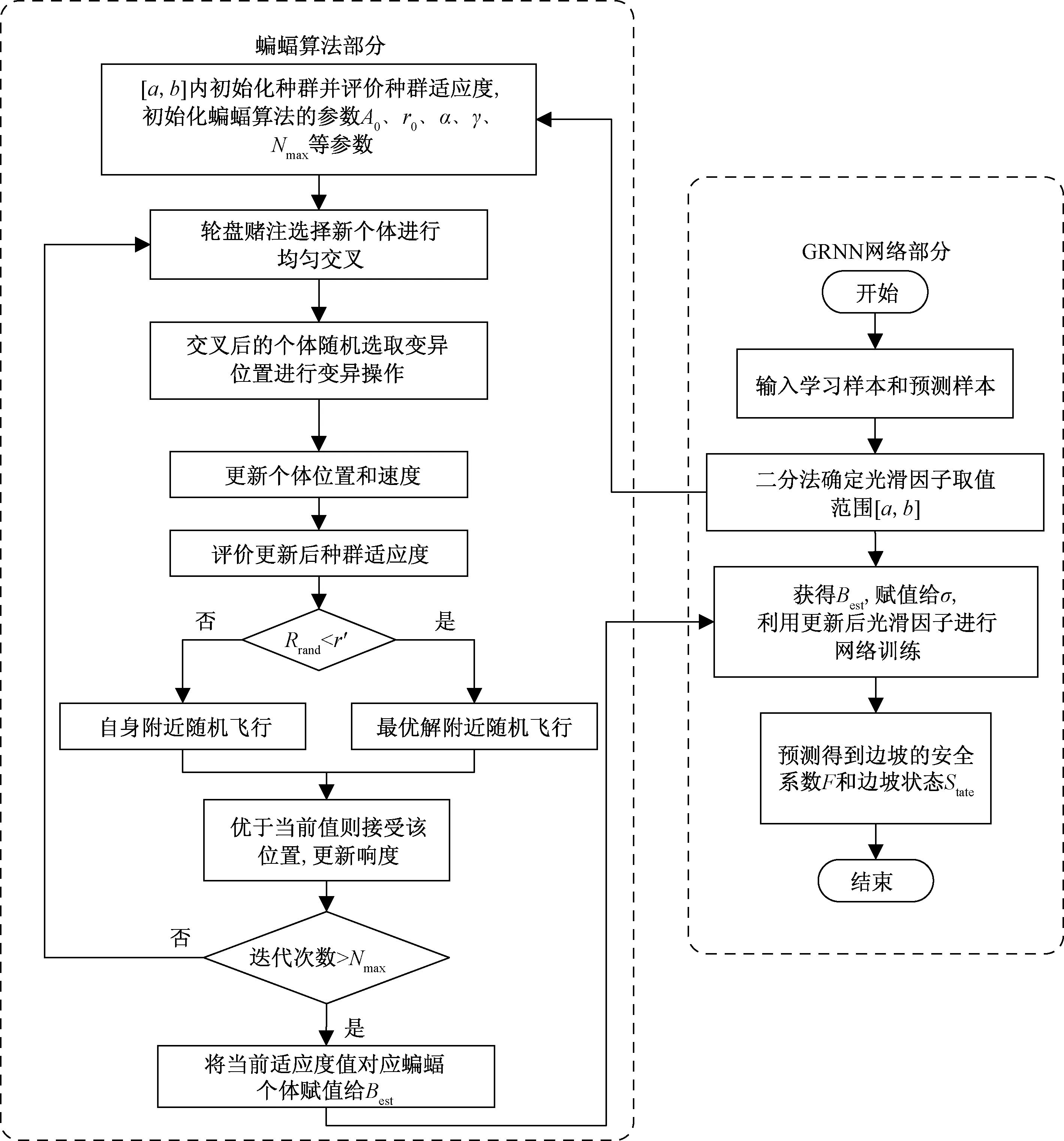
3 實例分析與結果對比




4 算例驗證


5 結論

