基于自適應(yīng)算法的彎曲河道斷面布設(shè)

張凌源 王超 劉林佳

摘要：針對(duì)現(xiàn)階段傳統(tǒng)斷面布設(shè)算法在彎曲河道斷面布設(shè)中的不足，提出一種河道斷面布設(shè)的自適應(yīng)算法。根據(jù)給定的水邊和河道中心線獨(dú)立生成每根斷面線，使得斷面線不僅能適配水邊，還能與河道中心線保持較高的垂直度，并對(duì)斷面線在彎曲河道的集束問題和相交問題進(jìn)行優(yōu)化處理，保證斷面線在河道內(nèi)均勻分布。為驗(yàn)證算法的可行性，選取3種類型河道地形進(jìn)行對(duì)比試驗(yàn)，并從主觀角度和客觀指標(biāo)對(duì)斷面布設(shè)效果進(jìn)行評(píng)價(jià)。試驗(yàn)結(jié)果表明，自適應(yīng)算法在保證斷面間距的前提下兼顧了斷面垂直度和分合理性，明顯優(yōu)于傳統(tǒng)算法。

關(guān)鍵詞：河道斷面布設(shè);自適應(yīng)算法;彎曲河道

中圖法分類號(hào)：P333.4 文獻(xiàn)標(biāo)志碼：A DOI：10.15974/j.cnki.slsdkb.2021.05.008

文章編號(hào)：1006 - 0081（2021）05 - 0030 - 03

1 研究背景

河道斷面線的布設(shè)一直是河道演變分析研究等的基礎(chǔ)性課題。現(xiàn)階段的水道地形測量基本上采用預(yù)設(shè)斷面線的走航法，所以開展對(duì)斷面線布設(shè)算法的研究尤為重要[1]。

目前，HYPACK水文測量軟件的斷面布設(shè)算法應(yīng)用最為廣泛，主要有內(nèi)插法、中心線法和平行線法。內(nèi)插法和平行線法的基本原理是根據(jù)已知斷面等距內(nèi)插或延伸，中心線法的原理是根據(jù)河道中心線等距垂直分布，這些算法在順直河道都取得了較好的效果，但是在連續(xù)彎曲河道則各有不足。內(nèi)插法在連續(xù)彎曲河道需要大量的人工控制斷面才能保證斷面與流向的垂直度，需要較多的人工干預(yù)[2]。中心線法能保證與流向具有較高的垂直度，但無法精準(zhǔn)控制斷面線的邊緣間距，往往會(huì)出現(xiàn)外彎超距和內(nèi)彎相交的現(xiàn)象，也不能較好地適配水邊線。平行線算法則完全不適用于彎曲河道[3]。針對(duì)上述斷面線布設(shè)算法的不足，本文提出一種自適應(yīng)算法，實(shí)現(xiàn)了斷面線和水邊線的高度契合，解決了彎曲河道斷面線的均勻分布問題。

2 傳統(tǒng)HPACK算法介紹

2.1 內(nèi)插法

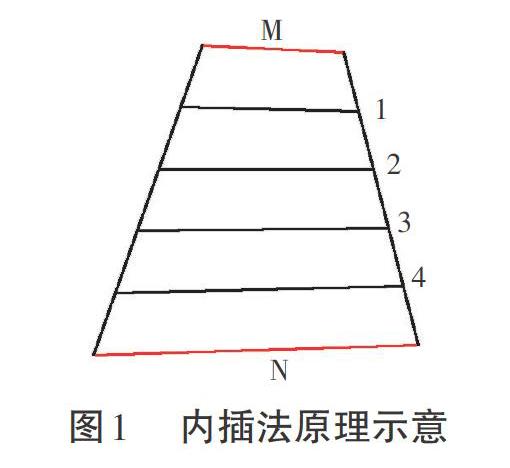
內(nèi)插法的原理如下：M和N為控制斷面，1，2，3，4為內(nèi)插斷面，內(nèi)插斷面的端點(diǎn)即為MN端點(diǎn)連線的等分點(diǎn)。使用內(nèi)插法布設(shè)斷面時(shí)，控制斷面的位置和數(shù)量決定最終的斷面布設(shè)效果。此算法一般適用于順直河道，在彎曲河道要達(dá)到較好的斷面布設(shè)效果，需人工布設(shè)大量控制斷面，對(duì)人工干預(yù)依賴程度較高，不利于斷面布設(shè)的自動(dòng)化[4]。內(nèi)插法原理見圖1。

2.2 中心線法

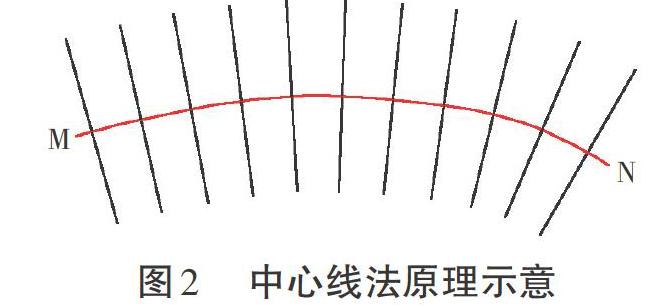
中心線法的原理是根據(jù)河道中心線的走向，在中心線上等距垂直分布斷面線。在順直河道的效果較好，但在連續(xù)彎曲河道效果不佳。該算法在河道外彎可能會(huì)出現(xiàn)斷面超距現(xiàn)象，在河道內(nèi)彎可能會(huì)出現(xiàn)斷面相交現(xiàn)象，而這些現(xiàn)象都是斷面布設(shè)中應(yīng)該避免的。該算法原理示意見圖2。

3 適配水邊的自適應(yīng)河道斷面算法

3.1 自適應(yīng)算法的特點(diǎn)

針對(duì)傳統(tǒng)算法所存在的問題，筆者提出了一種適配水邊的自適應(yīng)河道斷面算法，該算法具有如下特點(diǎn)。

（1）可以精準(zhǔn)控制斷面間距，控制精度達(dá)到0.01 m。為了保證斷面不出現(xiàn)超距現(xiàn)象，內(nèi)插法往往只能減小斷面距離參數(shù)，不僅無法精準(zhǔn)控制斷面間距，還導(dǎo)致斷面數(shù)量的非必要增多。中心線法則只能精確控制中心線上的斷面間距，邊緣間距則往往會(huì)出現(xiàn)超距或相交現(xiàn)象。

（2）可以根據(jù)水邊線的走向自動(dòng)適配，契合水邊，較傳統(tǒng)算法更為美觀且應(yīng)用性更強(qiáng)。

（3）可以較好地解決彎曲河道斷面布設(shè)的集束問題、相交問題和均勻分布問題。

3.2 自適應(yīng)算法的實(shí)現(xiàn)步驟

實(shí)現(xiàn)河道斷面自適應(yīng)算法需先準(zhǔn)備包含左右水邊線和河道中心線的 dxf文件，然后預(yù)設(shè)斷面間距d。具體實(shí)現(xiàn)步驟如下。

（1）分別讀取 dxf文件的左右水邊線、中心線的節(jié)點(diǎn)坐標(biāo)，根據(jù)節(jié)點(diǎn)坐標(biāo)進(jìn)行線性內(nèi)插，內(nèi)插間距0.01 m，用內(nèi)插點(diǎn)近似替代曲線。

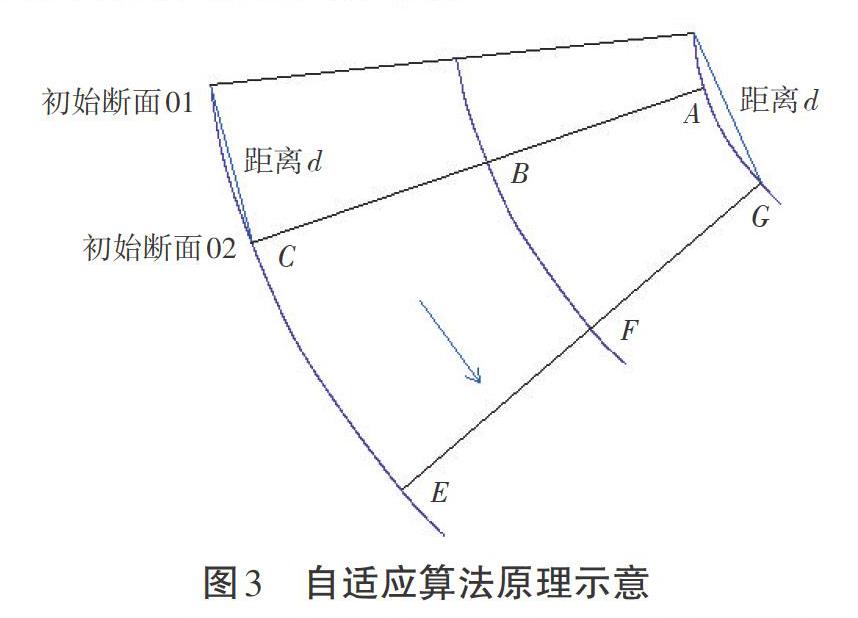
（2）自適應(yīng)算法原理見圖3。將左右水邊的端點(diǎn)連線視為初始斷面線。在左水邊選取距端點(diǎn)為d的點(diǎn)A，在中心線上選取距離A點(diǎn)最近的點(diǎn)B，再在右水邊上選取距離AB最近的點(diǎn)C，AC即為利用左水邊得到的斷面線。同樣，在右水邊選取距端點(diǎn)為d的點(diǎn)E，在中心線上選取距離E點(diǎn)最近的點(diǎn)F，再在左水邊上選取距離EF最近的點(diǎn)G，EG即為利用右水邊得到的斷面線。然后從AC、EG中選取一條距離初始斷面更遠(yuǎn)但又不超距的斷面，圖3中明顯AC更加合適，這樣就能得到02號(hào)斷面線，并以02號(hào)斷面線AC為分界點(diǎn)，舍棄之前的左右水邊點(diǎn)和中心線點(diǎn)。將02號(hào)斷面線AC視為初始斷面，循環(huán)上述過程，最終將得到全部斷面線。

（3）上述循環(huán)推進(jìn)的過程能保證斷面線與水邊契合，既不會(huì)超距，也不會(huì)相交，但不能保證斷面線在河道內(nèi)均勻分布。實(shí)際上，上述過程生成的斷面線會(huì)出現(xiàn)聚集現(xiàn)象，尤其是在河道內(nèi)彎部分，斷面分布并不均勻，如圖4所示。

（4）為解決斷面在河道內(nèi)彎的不均勻分布現(xiàn)象，需要在算法上對(duì)斷面線進(jìn)一步優(yōu)化。先定義距離值DD，如果兩條斷面線之間的間距小于DD，則視這兩條斷面線之間的區(qū)間為密集區(qū)間，比如圖4中的（8，13），（15，17），先找出所有密集區(qū)間，并對(duì)所有密集區(qū)間進(jìn)行前后擴(kuò)展，比如（8，13）則擴(kuò)展為（3，18），（15，17）則擴(kuò)展為（10，22）。再將有交集的擴(kuò)展區(qū)間進(jìn)行合并，如（3，18），（10，22）合并為（3，22），直到各擴(kuò)展區(qū)間之間都沒交集，即可得到最終的優(yōu)化區(qū)間。

（5）本算法中，優(yōu)化區(qū)間一般擴(kuò)展為密集區(qū)間的3倍以上，比如密集區(qū)間（8，13）包含6根斷面，優(yōu)化區(qū)間（3，22）則包含20根斷面。如果直接將優(yōu)化區(qū)間內(nèi)的斷面線直接重新均勻分布，往往會(huì)因?yàn)樯婕暗臄嗝孢^多，導(dǎo)致分布后的斷面與河道中心線垂直度不夠。因而需要結(jié)合測量比例尺和自然河道的彎曲情況選擇合適的參數(shù)對(duì)優(yōu)化區(qū)間進(jìn)行分割，進(jìn)而得到最終的優(yōu)化子區(qū)間，對(duì)優(yōu)化子區(qū)間內(nèi)的左右斷面端點(diǎn)分別重新等距分布，即可得到最終的斷面線，如圖5所示。

在算法中，根據(jù)輸入的參數(shù)對(duì)優(yōu)化區(qū)間進(jìn)行分割，參數(shù)越大，分割后的優(yōu)化子區(qū)間越大，最終的斷面分布越均勻;參數(shù)越小，分割后的優(yōu)化子區(qū)間越小，最終的斷面與河道中心線垂直度越高，所以對(duì)于不同彎曲程度的河道，參數(shù)的選擇也會(huì)不同。自適應(yīng)算法流程見圖6。

4 試驗(yàn)結(jié)果與分析

為檢測各算法的效果，特選取武漢市蔡甸區(qū)內(nèi)的漢江河段，該河段為典型的連續(xù)彎曲河段，河道長8.7 km，分別運(yùn)用3種算法獨(dú)立生成斷面，斷面間距參數(shù)為40 m。其中，自適應(yīng)法輸入?yún)?shù)為40 m，內(nèi)插法人工控制斷面線為18根，中心線法分別輸入?yún)?shù)為40，35和30，斷面統(tǒng)計(jì)情況見表1。

從表1中的各項(xiàng)指標(biāo)參數(shù)可分析出各算法的斷面布設(shè)效果：

（1）自適應(yīng)算法的各項(xiàng)指標(biāo)參數(shù)表現(xiàn)最為突出，綜合性能最佳。

（2）隨著人工干預(yù)斷面的增多，內(nèi)插算法布設(shè)效果可以逐漸接近自適應(yīng)算法，但是自動(dòng)化程度會(huì)越來越低，不利于推廣應(yīng)用。

（3）中心線算法自動(dòng)化程度與自適應(yīng)算法相當(dāng)，但普遍存在斷面超距現(xiàn)象。隨著輸入?yún)?shù)變小，逐漸降低超距占比的同時(shí)，斷面總數(shù)又會(huì)明顯多于另外兩種算法。

5 結(jié) 論

通過對(duì)自適應(yīng)河道斷面算法的論述和分析，可得出如下結(jié)論：①該算法能實(shí)現(xiàn)較高程度的自動(dòng)化斷面布設(shè)。②該算法能精確控制斷面間距，較高程度契合水邊線。③該算法能滿足不同比例尺的斷面布設(shè)要求，在保證斷面垂直度的前提下實(shí)現(xiàn)河道斷面線的均勻分布。

參考文獻(xiàn)：

[1] 楊志剛. 關(guān)于水文測驗(yàn)斷面測量方法的思考[J]. 水土保持應(yīng)用技術(shù)， 2018（1）： 47-48.

[2] 王建英，黃德武.? 基于插值法和擬合法的水文大斷面繪制方法[J].? 人民長江， 2020， 51（6）：96-100，206.

[3] 趙學(xué)民， 王衛(wèi)平， 張宗德.? HYPACK水文測量軟件在水下地形測量中的應(yīng)用[J].? 水文， 2000， 20（3）：38-40.

[4] 張立華，殷曉冬. 水深測量計(jì)劃測線布設(shè)與航跡控制算法[J]. 海洋測繪，2002，22（2）：33-35.

（編輯：唐湘茜）

Abstract：Aiming at the shortcomings of the current algorithm of flow measuring vertical line layout across cross-section in curved river， an self-adaptive algorithm for flow measuring vertical line layout is proposed. This algorithm generates each vertical line independently according to the given water frontier and the river centerline ， so that the vertical line can not only adapt to the water frontier， but also maintain a relatively high perpendicular to the river centerline， and optimize the clustering and intersection problems of the vertical lines in curved river to ensure that the vertical lines are evenly distributed across the rivers. In order to verify the feasibility of the algorithm， three different river topographies were selected for comparative analysis， and the effect of vertical line layout was evaluated subjectively and objectively. The analysis results show that by the adaptive algorithm， both the higher perpendicular to the river centerline and the reasonable distribution of the vertical lines can be obtained under the assurance of evenly distribution vertical lines， which is significantly better than traditional algorithms.

Key words： layout of flow measuring vertical line; adaptive algorithm; curved river