雙向通信無人機集群領航頂點選取方法
戴麗
(國防科技大學 文理學院,湖南 長沙 410073)
多智能體系統控制技術是人工智能時代的研究熱點之一[1],其成果可用于多個領域,如智能交通、機器人編隊,甚至是軍事用途,如無人機蜂(狼)群作戰等。無人機集群作為一種特殊的多智能體系統,個體無需全局通信,僅通過對其周圍一定范圍內個體間的通信、合作和協調等就可以表達集群整體結構和功能。它在自組織能力、推理能力,以及對未知環境的適應性等方面有很多潛在應用。
無論是地面起飛式無人機集群,還是空投式無人機集群,其控制技術的難點都在于隊形控制,核心在于解決可行性和有效性兩個問題[2]:可行性是研究無人機集群能不能全局可控,使之形成所有預定隊形;有效性則回答了最少需要輸入多少信號,才能達到全局可控。最小領航集選取與這2個問題密切相關。
對于通信網絡拓撲結構圖為有向圖的領航跟隨網絡系統,文獻[3]通過引進匹配概念,使有向網絡的可控性問題已得到較好解決。但是,對于無向領航跟隨網絡系統控制而言,正如Kumar等[4]于2019年所指出的那樣:如何選取領航頂點、如何選取最少個數的領航頂點都是尚待解決的難題。
目前,無向網絡控制技術已經引起人們的廣泛關注。文獻[5]是一篇較早關注無向網絡可控性的文章,該文通過Kalman秩條件給出了無向網絡可控的充要條件。研究無向網絡領航集常用的圖結構有:強制零點集(zero forcing set, ZFS)[4,6-8]、約束匹配(constraint matching, CM)[8-11]和非平凡等價劃分(nontrivial equitable partition,NEP)[12-15]等。已有的研究成果表明無向網絡可控當且僅當領航集是推廣的ZFS,且Shima等[8,10]發現了網絡中ZFS與CM之間具有等價關系。基于NEP概念人們給出了網絡可控的必要條件,同時也證明了網絡可控當且僅當它的每個連通分支可控。
Ji等[16-17]則是通過Laplace矩陣的特征向量研究無向網絡的可控性,其中文獻[16]給出了無向網絡可控的充要條件,文獻[17]則給出DCD、TCD等破壞網絡可控性的頂點集圖特征。文獻[18-19]證明了高階時不變系統的可控性等價于一階(線性)時不變系統的可控性,通過Laplace矩陣的特征向量給出了無向網絡可控的充要條件,同時指出了使網絡可控的2個方法:增加領航頂點和修改網絡權值。
這些研究關注重點在于從理論上給出領航集的代數特征或圖論特征,所舉算例規模較小。對于僅具有單特征值的無向網絡系統,可以從代數角度給出領航集。理論研究表明,當網絡中個體數量趨向無窮時,網絡Laplace矩陣僅具有單特征值的概率趨向1。但是,對于無人機集群系統,個體數量大多在幾十至幾百之間,這類系統的Laplace矩陣具有多重特征值的可能性很大。現有的研究很少涉及求解這種規模無向網絡領航集的算法。
復雜網絡的相關研究值得借鑒。Hamdan等[20-21]采用啟發式算法求復雜網絡的領航集,之所以采用啟發式算法求領航集是因為這一問題是NP難問題。在無向復雜網絡的可控性研究中,多采用攜帶更多信息的可控性Gramian矩陣[22-23]。Katherine等[24]研究了平均可控性以及可控性與魯棒性的關系,并給出使樹圖可控的領航集選取方法。2020年,基于頂點分類文獻[25]提出大規模動態系統的最小領航頂點選取問題的算法。
本文針對具有幾十個個體的無向領航跟隨模式無人機集群領航頂點選取問題,研究領航頂點的圖特征,解決具有何種圖特征的頂點必須成為領航頂點,以及如何求出最小領航集這2個問題;給出求領航集的算法并用數值仿真實驗驗證算法的有效性,分析無人機集群領航集的數值特征。
1 基本理論
1.1 無人機集群通信網絡的圖論模型
無人機個體間的通信關系可用圖表示。設圖G=(V,E) ,其中頂點集V={v1,v2,···,vn},vi表示第i個無人機個體,邊vi,vj∈E當且僅當第i個無人機與第j個無人機間可通信,G稱為通信網絡拓撲結構圖。若無人機個體間的通信關系是單向的,則G為有向圖;若無人機個體間是雙向通信的,則G為無向網絡。
對于領航跟隨模式的無人機集群,接收外界輸入控制信號的個體稱為領航頂點,其余頂點則稱為跟隨頂點。本文考慮有n個無人機個體的線性時不變系統,個體的動力學方程描述為

式中:xi為第i個無人機的狀態信息;ui為外界輸入控制信息。如圖1,由Kalman秩條件[5]知,取v1或v3作為領航頂點,則系統可控;若取v2作為領航頂點,則系統不可控。
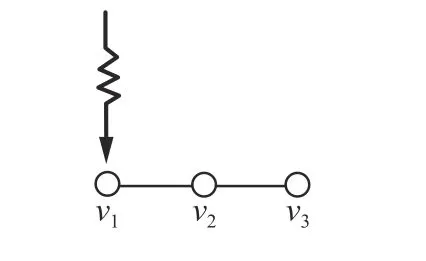
圖1 領航集的選取對系統可控性影響Fig.1 Influence of leader’s selection on the controllability of the systems
1.2 預備理論
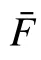
研究結果表明,無向網絡可控性與Laplace矩陣L的特征值和特征向量有關。
性質1[16-18]設F為跟隨集,則無向網絡線性時不變系統式(1)可控,當且僅當L與LF→F沒有共同特征值。
性質2給出領航集的代數特征。值得注意的是,性質2中的特征向量y是Laplace矩陣L的任意一個特征向量,因此,當L有多重特征值時,并不能僅通過考察它的所有線性無關的特征向量得到領航集,而應進一步驗證全部具有零分量的特征向量。從數值計算角度而言,這種驗證計算量大,難以實現。本文將從領航頂點的圖特征出發,給出確保系統可控的領航集求解算法。
2 關鍵集和完美關鍵集
由性質2可知,對于非空頂點集T,若通信網絡拓撲結構圖G的Laplace矩陣L有一個特征向量y使得yT=0 , 則該頂點集T不能作為領航集,也就是說,此時為使無人機集群可控,必須將T的補集中某些頂點加入到領航集。基于此,本文提出關鍵集的概念。
2.1 關鍵集
定義1 關鍵集。設非空頂點集S?V,L為通信網絡拓撲結構圖G的Laplace矩陣,若存在L的一個特征向量y使得ySˉ=0,則稱頂點集S為關鍵集(critical set, CS)。若 |S|=k,則稱S為k關鍵集(kcritical set)。
定義2 完美關鍵集。設S為關鍵集,若存在L的一個特征向量y使得yv≠0(?v∈S),則稱S為完美關鍵集(perfect critical set, PCS)。若 |S|=k,則稱S為k完美關鍵集(kperfect critical set)。
定義3 最小完美關鍵集。設S為關鍵集,若它的任何真子集都不再是關鍵集,則稱S為最小完美關鍵集(minimal perfect critical set, MPCS)。若 |S|=k,則稱S為k最小完美關鍵集(kminimal perfect critical set)。
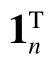
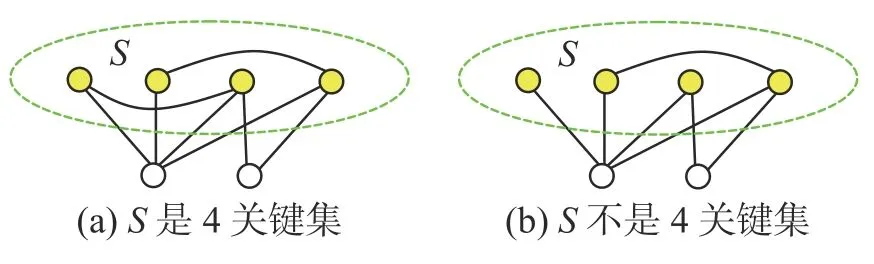
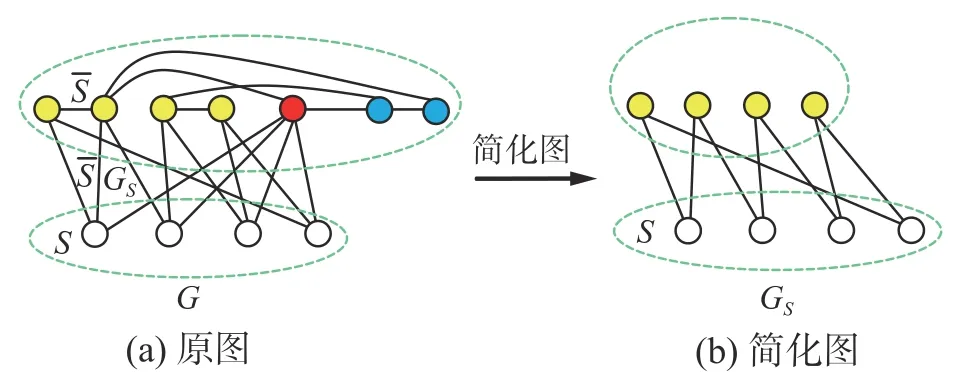
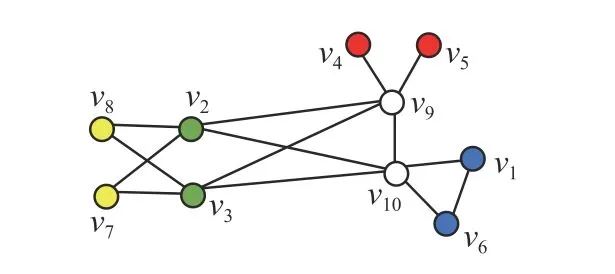
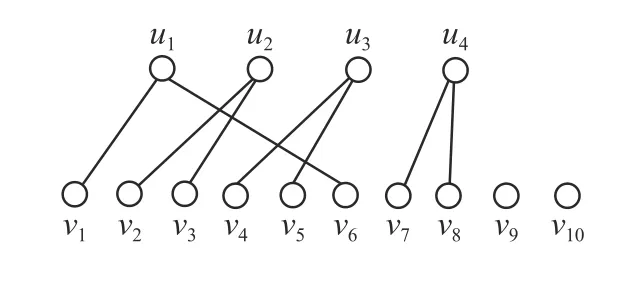
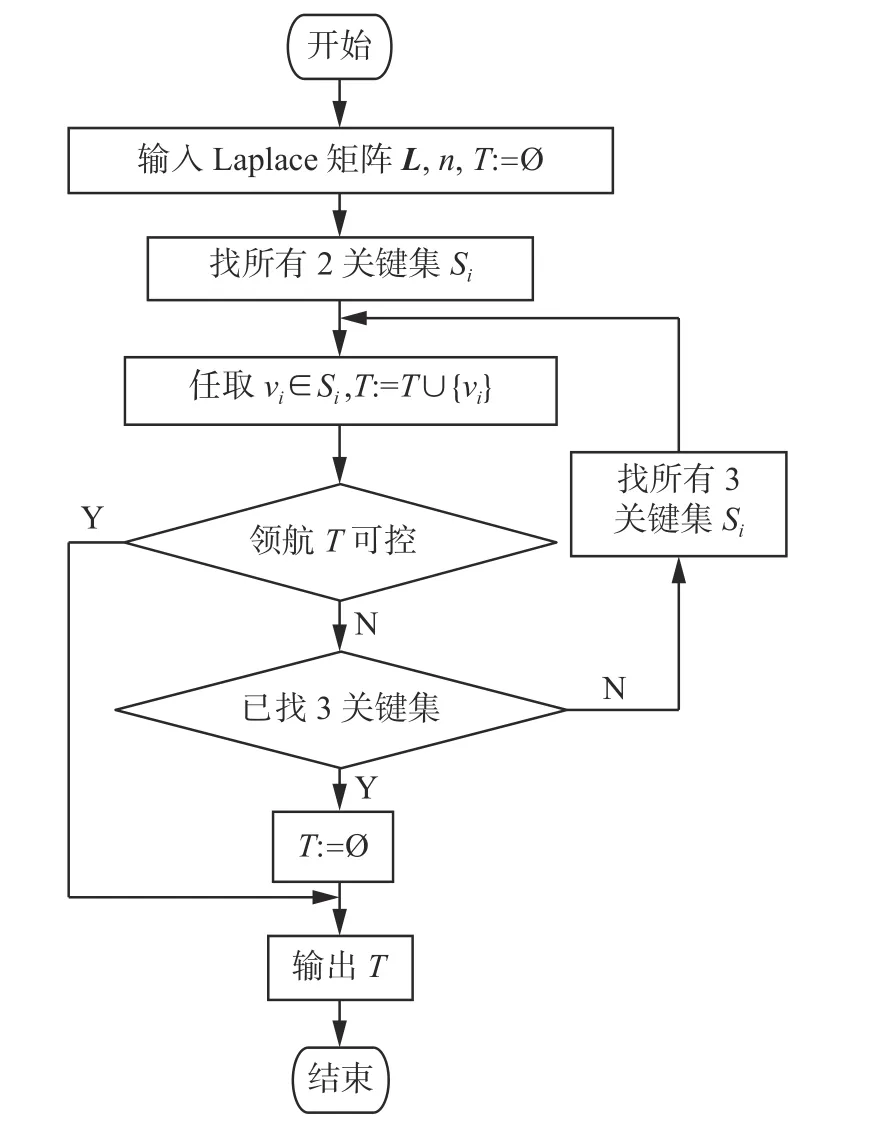
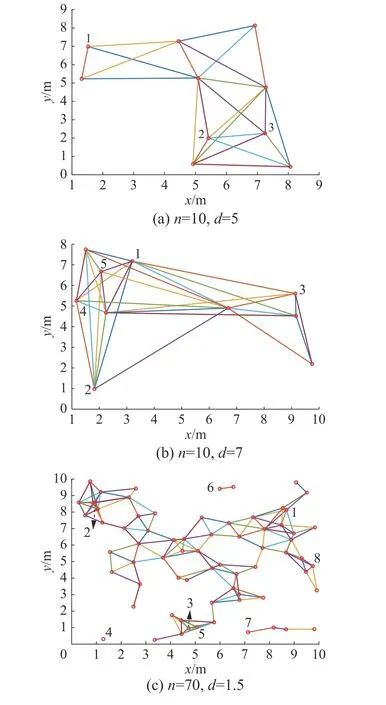
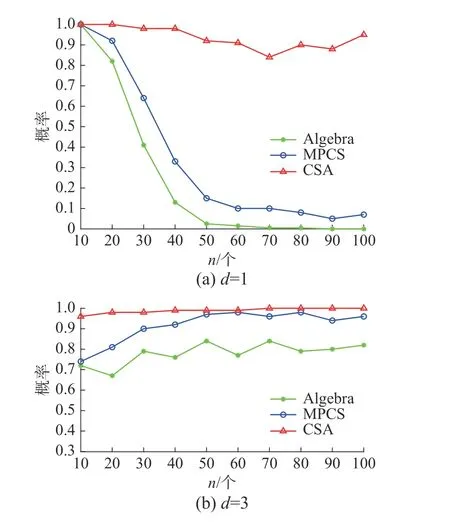
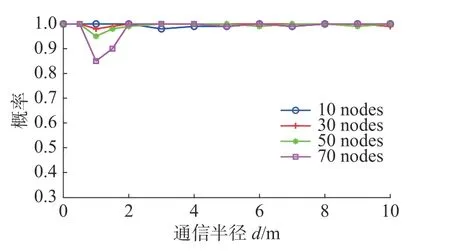
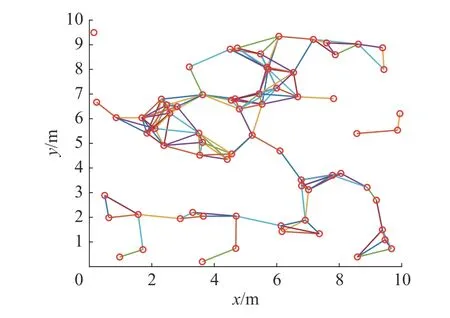
由k關鍵集的定義可知,k為正整數且k 定理1n階連通無向網絡不存在1關鍵集。 若S為1關鍵集,不防設S={v1}, 則由ysˉ=0 及式(2)可知yS=0, 于是y=0 與y為特征向量矛盾。 由性質2及定理1知推論1、2成立。 推論1 設G為n階連通無向網絡,S?V且|S|=n?1,若取S為領航集,則系統可控。 推論2 設n階無向網絡G為非連通圖,則G有1關鍵集的充要條件是G中有孤立頂點。 由定理1可知,對于n階連通無向網絡的k關鍵集,必有 2 ≤k≤n?1。 定理2 設頂點集S?V且 |S|≥2 ,若 ?v∈Sˉ,v要么與S中所有頂點都相鄰,要么與S中所有頂點都不相鄰,則S為關鍵集。 情況1 若矩陣LS→S?mI|S|只有零特征值。 此 時 必 有LS→S?mI|S|=0|S|×|S|。 注 意 到 ?v∈Sˉ ,若v與S中頂點都相鄰,則其在矩陣LSˉ→S中對應的行向量Lv→S分量全為1;若v與S中頂點都不相鄰,則其對應的行向量Lv→S分量全為0。 因此,構造n階列向量y=[1?|S|1···10···0],則易見y為Laplace矩陣L的特征向量。 情況2 若矩陣LS→S?mI|S|有非零特征值。 此 時 取LS→S?mI|S|的 特 征 值 λ′≠0,令λ=λ′+m,則λ 為LS→S的特征值且λ ≠m。 設yS為矩陣LS→S相應于特征值 λ (λ≠m) 的特征向量,構造n階列向量y=[yS0],則有 由LS→SyS=λyS知 由定理2可知圖1中的頂點集 {v1,v3} 是關鍵集,所以v2不能作為領航頂點。 在一定條件下,運用定理2判斷一個頂點子集S是否為關鍵集時,可以不考慮Sˉ 中那些與S中頂點都相鄰或者都不相鄰的頂點。 設特征向量y是與k完美關鍵集S對應的特征向量,即ySˉ=0 且y的非零分量恰有k個,于是有引理1。設 [ {v},S] 表示一個端點為v另一個端點屬于S的邊集。 引理1 設S為k完美關鍵頂點集,則?v∈Sˉ ,有 |[ {v},S]|≠1 且 |[ {v},S]|≠k?1。 證明 設S={v1,v2,···,vk} 為k完美關鍵集,存在y=[y1y2···yk0 ···0]T為Laplace矩陣L的特征向量。由S為k完美關鍵集知yi≠0(i=1,2,···,k)。 再由式(2)知yk=0, 矛盾。 由定理1知,2關鍵集是2完美關鍵集,也是2最小完美關鍵集。 證明 由定理2知充分性成立。只須證明必要性。 證明 由定理2知充分性成立。只須證明必要性。 由定理3可知,2關鍵集實際上就是文獻[26]給出的twins頂點對,由此可見,2關鍵集是twins頂點對的推廣。但與文獻[17]中所提出的DCD頂點對不同,DCD頂點對考慮的是在跟隨集中的2個頂點,而2關鍵集考慮的對象則是所有頂點。 另外,定理3和定理4表明頂點集S能否成為2關鍵集或3關鍵集與S中的頂點是否相鄰無關。但是,當S中頂點數更多時,該結論不一定成立。如圖2中4個深色頂點構成的頂點集S,當S中頂點的相鄰關系如圖(a)時,它是4關鍵集;但當S中頂點的相鄰關系如圖(b)時,它不再是4關鍵集。 圖2 4關鍵集與G[S]的關系Fig.2 Relationship between four critical set an G[S] 若S={v1,v2,···,vk} 為獨立集且為k完美關鍵集,則Laplace矩陣L有一個特征向量: y=[y1y2···yk0 ··· 0]T yi≠0,i=1,2,···,k 由S為獨立集知 ?vi∈S有: 即dG(v1)=dG(v2)=···=dG(vk)=λ。亦即當S為獨立集時,完美關鍵集S中頂點度均相等。基于此,定理5給出了獨立集成為關鍵集的一個充分條件。 證明 不防設S={v1,v2,···,vk} 且S中所有頂點在圖G中的度均為d。若簡化圖GS為空圖,則由定理2知結論成立,下設GS非空圖。 取y=[x1x2···xk0 ···0]T, λ=d,則有 綜上可知Ly=λy, 即向量y為Laplace矩陣的特征向量,由于ySˉ=0,故由定義1知S為關鍵集。 圖3 簡化圖及其關鍵集Fig.3 Simplification of graph G and its CS 基于關鍵集的概念,本節討論如何求出無人機集群最小領航集的算法。 由性質2及關鍵集的定義知定理6成立。 定理6 設F為跟隨集,F為領航集,則雙向通信無人機集群線性時不變系統(見式(1))可控當且僅當F中不包含關鍵集。 證明 由性質2知系統(見式(1))可控當且僅當yFˉ≠0 ,其中y是任意一個特征向量。由定義1知,yFˉ≠0 當且僅當F不是關鍵集且不包含任何關鍵集。 設S1,S2,···,Sm是無人機集群通信網絡拓撲結構圖的所有關鍵集,構造二部圖H=(U,V;E),頂點集U={u1,u2,···,um} ,其中ui與Si對應;V=V(G)={v1,v2,···,vn}為無人機集群通信網絡拓撲結構圖G的頂點集,viuj∈E(H) 當且僅當vi∈Sj。若viuj∈E(H) 則稱頂點vi覆蓋關鍵集Sj。由定理6可知求最小領航集等價于求覆蓋所有關鍵集的最小頂點集T(T?V)。 基于定理6,本節給出求領航集的算法(critical set algorithm, CSA): 1)求出無人機集群通信網絡拓撲結構圖G的所有k關鍵集Si(i=1,2,···,m); 2)構造二部圖H=(U,V;E); 3)求最小頂點集T(T?V) 使T中的頂點覆蓋所有關鍵集,則T即為最小領航集。 例如,圖4中G來自文獻[15],由定理3知它有2關鍵集S1={v1,v6} 、S2={v2,v3} 、S3={v4,v5}、S4={v7,v8};由定理4知該圖沒有3關鍵集;由于2個懸掛點v4、v5都與v9相鄰,故由引理1知v9不屬于任何完美關鍵集;同理,考慮v1和v6這2個頂點可知v10也不屬于任何關鍵集。從而,容易知道圖4中不存在5完美關鍵集;對于4完美關鍵集只能是上述4個Si(i=1,2,3,4) 中每個集合各取一個構成的集合,容易驗證它們都不是關鍵集。即上述4個Si(i=1,2,3,4) 是該網絡的全部最小完美關鍵集。 圖4 圖G及其關鍵集Fig.4 Graph G it’s critical set 于是可構造二部圖H=(U,V;E) 如圖5所示。從該二部圖中可以看出每個頂點vi只能覆蓋一個uj,于是從每個uj的相鄰頂點任取一個組成的集合就是圖G的最小領航集,比如可取T={v1,v2,v4,v7}為最小領航集。 圖5 二部圖Fig.5 Bipartite graph 本算例說明如何運用關鍵集求出無人機集群通信網絡拓撲結構圖的最小領航集。 一般地,CSA算法的1)和3)都不是多項式時間的算法。但是,基于本文給出的定理,求出相應特殊的關鍵集及領航集則是多項式時間算法,具體的算法流程如圖6所示。 圖6 CSA算法流程Fig.6 Flow chart of CSA 由定理3知,在CSA算法流程圖中找出所有2關鍵集的算法復雜性為O(n3)。由定理4知,找所有3關鍵集的算法復雜性為O(n4),因此,圖6所示的CSA算法復雜性為O(n4)。 在實驗中,設無人機集群的初始位置隨機,經過一段時間后形成穩定的通信網絡拓撲結構圖,并在后續保持通信關系不變。在具體的數值實驗中,程序將在 1 0×10 平面區域內隨機生成n個頂點,代表n個無人機個體的初始位置,設無人機個體的通信半徑為參數d。圖7是實驗中隨機生成的3個通信網絡拓撲結構圖G。 圖7 無人機集群的通信網絡拓撲結構Fig.7 Topology of communication network for UAVs 其中,圖7(a)是通信半徑為5時隨機生成的具有10個無人機個體的通信網絡拓撲結構圖,CSA算法求出的領航集為 { 1,2,3};圖7(b)是通信半徑為7時隨機生成的具有10個無人機個體的通信網絡拓撲結構圖,CSA算法求出的領航集為{1,2,3,4,5};圖7(c)是70個無人機個體通信半徑為1.5時生成的通信網絡拓撲結構圖,CSA算法求出的領航集為 { 1,2,···,8}。 實驗1 代數方法、圖論方法及CSA算法的對比實驗。 在代數方法中,首先對于單重特征值,先求它的1個特征向量,若該特征向量的非零分量對應的頂點集不是頂點集V,由定義1知,這些非零分量對應的頂點集是1個關鍵集,在該關鍵集中任取1個頂點放入領航頂點集;其次,對于多重特征值,設它的重數為m(m≥2),由于這種特征值對應的特征向量可能具有不同的非零分量集合,因此,這種特征值可能對應多個不同的MPCS,程序對具有相同非零分量的特征向量進行識別并重新認定該特征值的重數m1(m1≤m)。在特征向量的非零分量中任取m1個對應頂點放入領航頂點集。 在圖論方法中,程序基于本文給出的定理2~5,求出2關鍵集、3關鍵集和孤立關鍵集等一些特殊的關鍵集。然后,在每個關鍵集中任取一個頂點放入領航頂點集。 CSA算法則是將代數方法和圖論方法相結合求關鍵集。對于單重特征值,程序用代數方法求它的關鍵集;對于多重特征值,則用圖論方法求出2關鍵集、3關鍵集。實驗結果如圖8所示。 從圖8中可以看出,通過引入圖論理論求關鍵集,使得求解效率得到大幅度提高,特別是當通信半徑d=1 時,單純的代數方法或圖論方法都難以搜索到領航集,但將兩者相結合的CSA算法仍然使得求解效率在80%以上。實驗表明,代數方法能找到一部分領航頂點,而圖論方法則可以找出另一部分領航頂點,CSA正是借助關鍵集概念,將代數方法和圖論方法統一用于構建最小領航頂點集。 圖8 對比實驗Fig.8 Comparison of experimental results 實驗2 CSA算法的求解效率與無人機個體通信半徑間關系。 在本實驗中,針對不同的無人機個體數目,測試CSA算法在不同通信半徑條件下的求解效率,實驗結果如圖9所示。 圖9 CSA算法求解效率與通信半徑的關系Fig.9 Relationship between the efficiency of CSA and communication radius of UAV 從圖9中可以看出,盡管CSA算法在求解過程有一定程度的抖動,但當頂點個數小于30時,求解效率在95%上。一個有趣的現象是,當頂點個數大于30時,若其通信半徑介于3~9,則CSA算法幾乎100%可以找到領航集;若通信半徑小于3或大于9,則CSA算法都出現了不同程度的抖動,特別是當通信半徑介于0.5~3時,算法求解效率較差。出現這一現象的原因在于,此時圖中單重特征值減少而多重特征值增加,這使得同一特征值對應的關鍵集增加,而基于本文給出的定理2~5,CSA算法只求出2關鍵集、3關鍵集和孤立關鍵集等一些特殊的關鍵集,從而使得算法難以找到領航集。例如,見圖10,該無向網絡的特征值中,除單重特征值外,還有1個3重特征值、1個4重特征值和1個5重特征值,CSA算法難以找到它的領航集。這說明,當頂點個數多且通信半徑較小時,圖中的關鍵集情況較復雜,需要進一步從理論上研究k關鍵集的圖特征。 圖10 復雜特征值情況的網絡結構Fig.10 Description of networks with multiple eigenvalues 實驗3 領航頂點個數與邊數關系。 隨著無人機個體和邊數的變化,領航頂點的個數也會相應地變化,因此,本實驗不考慮領航頂點個數的絕對值,而是考慮“領航頂點個數/無人機個體數量n”與“邊數/總邊數(即完全圖中的邊數n(n?1)/2)”間的關系。 實驗結果如圖11所示。從圖11中可以看出,隨著邊數占比趨于1,領航頂點占比趨于(n?1)/n;隨著邊數占比趨于0,領航頂點占比趨于1;特別是,領航頂點占比達最小。從圖11中可以看出,當無人機個體數量為10時,領航頂點占比達最小的情況出現在邊數占比為0.6~0.7;當無人機個體的數量為30時,領航頂點占比達最小的情況出現在邊數占比為 0.4~0.6;當無人機個體的數量為50(70)時,領航頂點占比達最小的情況出現在邊數占比為 0 .1~0.3。也就是說,從整體上看,所有“領航頂點占比與邊數占比”曲線都是下凸曲線,無人機個體數越多,曲線越向下凸且極小值點越向“左”偏。這一現象說明,若用較少個數的無人機個體控制整個無人機集群,則通信網絡拓撲結構圖中的邊數應取值于適當范圍,實驗3從統計意義上給出了這個范圍。 圖11 領航頂點個數與邊數的關系Fig.11 Relationship between the number of leaders and edges 本文以幾十架無人機構成的無人機集群為應用背景,利用Laplace矩陣的特征向量提出關鍵集概念,指出領航集所必須具備的圖特征,即領航集需覆蓋所有關鍵集。給出了2關鍵集和3關鍵集的圖特征,從圖論角度給出獨立集成為關鍵集的一個充分條件。數值實驗表明,基于關鍵集,CSA算法在大多數情況下能以90%以上的概率搜索到領航集。 如何刻畫k(k≥4) 關鍵集的圖特征是需進一步研究的內容。這是十分難以解決的問題,比如由圖2知4關鍵集與這4個頂點的相鄰關系有關,全體4階互不同構的簡單圖有11個,其中邊數為0、1、2、3、4、5、6的圖的個數分別為1、1、2、3、2、1、1。而全體5階互不同構的簡單圖有34個。隨著k的增加,k(k≥4) 關鍵集的情況異常復雜。但是,這又是一個十分有意義的問題。比如,從數值實驗可以看出,僅依據本文給出的定理2~5求出有限特殊的關鍵集,CSA算法就能在大多數情況下以90%以上的概率搜索到領航集。 另外,從圖論角度給出領航集的充要條件,最小領航頂點數的上、下界等也都是值得進一步研究的問題。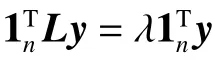
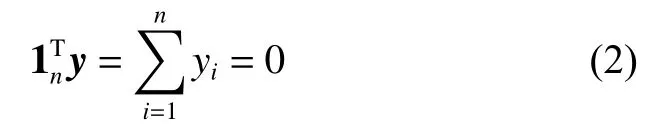
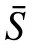

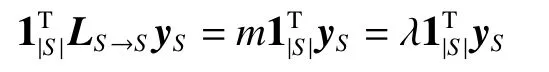

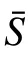

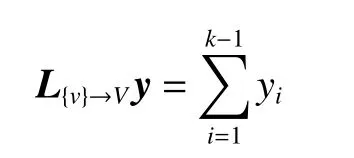
2.2 2關鍵集和3關鍵集的圖特性

2.3 獨立關鍵集的圖特征

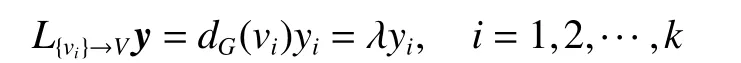
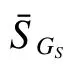
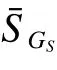
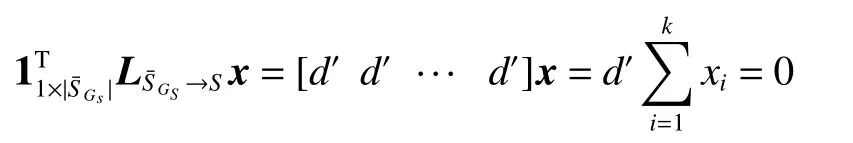
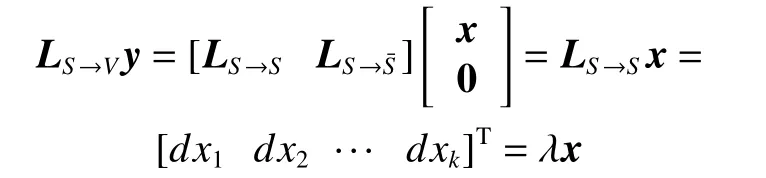
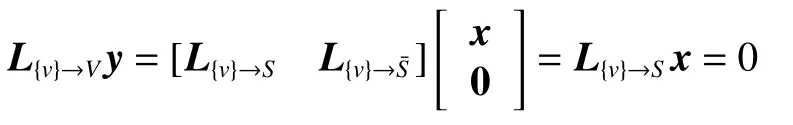
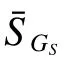
3 最小領航集
3.1 算法理論基礎
3.2 最小領航集算法
3.3 CSA算法復雜性分析
3.4 數值實驗及分析

4 結束語

