基于模糊BP神經網絡雷達導引頭的性能評價?

岳 炯 呂衛民 胡文林

（海軍航空大學 煙臺264001）

1 引言

20世紀六十年代，美國加州大學Zedeh在集合論的基礎上研究了模糊數學處理方法［1］，提出了模糊集、隸屬函數、語言變量和模糊推理的概念，隨后又提出了模糊邏輯理論的概念，首次將模糊理論和人工智能發展方向聯系在一起。1992年第一屆模糊系統的國際會議首次召開及專刊IEEE Transac?tion on Fuzzy system的創辦［2］，標志著模糊理論成為一個具有重要意義的新的研究領域。

模糊神經網絡是將模糊系統和神經網絡結合在一起，以神經網絡為基礎，利用模糊系統將各環節參數模糊化，將運算規則模糊化的新型算法。模糊神經網絡有多種組合形式，目前應用較為廣泛的是利用神經網絡進行模糊邏輯推理，新的結合模型一方面具有模糊邏輯推理強大的結構表達能力，另一方面又具有神經網絡強大的學習適應能力。

2 模糊系統

在經典集合理論中，兩個集合的關系只有“屬于”和“不屬于”兩種狀態，但是在實際應用中，往往不會把界限劃分的這么明顯，比如：A的年收入比B多很多，這個“很多”表達的意思比較模糊，沒有明確的定義界限，就是個模糊集合。1965年，美國加州大學Zedeh以集合論為基礎研究了模糊數學處理方法，有效解決了模糊性事件的定量描述，創造師，研究方向：裝備系統工程。胡文林，男，博士研究生，研究方向：系統工程。了模糊理論新的研究領域。

2.1 模糊集合和隸屬函數

1）模糊集合。模糊集合是經典集合論的推廣，在經典集合理論中，對兩個集合之間的“屬于”和“不屬于”關系的特征函數描述只有“1”和“0”兩個表達方式［3］。

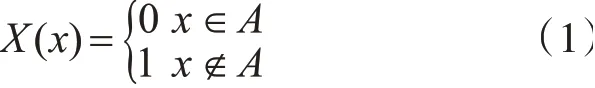
Zedeh將經典集合理論中特征函數的取值范圍由簡單的數字集合{0 ，1}延伸到可連續取值的閉區間[0 ，1]。同時引入了模糊集的概念，記論域U中一模糊集為A，A的隸屬函數為μA，μA(u)表示的是論域中元素u對模糊集A隸屬程度的大小，兩個模糊集相等則其分別對應的隸屬函數也相等。

2）隸屬函數。隸屬函數如上所述，是表示與模糊集合接近程度的函數，反映事物走向的一個漸變過程，通過得到集合的隸屬函數，能夠對模糊集合進行定量分析［4］。在給定論域U上的一個模糊集合A用一個取值在［0，1］范圍內的隸屬函數μA(u)來表示，當u隸屬A程度越大，μA(u)的取值越接近于1，當u隸屬A程度越小，μA(u)取值越接近于0。即U隸屬集合A的程度表示為

常見隸屬函數主要有高斯函數和三角型隸屬函數兩種［5］。

（1）高斯函數［6］。高斯函數表達式為

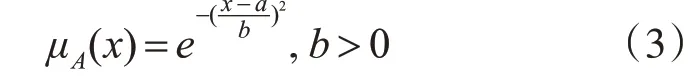
（2）三角型隸屬函數［7］。三角型隸屬函數表達式為

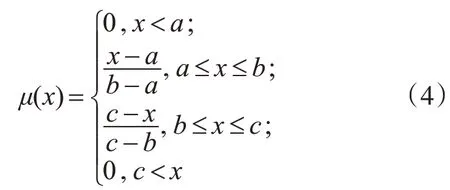
2.2 模糊邏輯

在模糊集合中，對模糊概念或模糊性事物的描述語句稱作模糊命題，模糊命題［8］是普通命題的推廣，其運算法則同模糊集合運算類似。模糊命題是指具有模糊性的陳述句，通常用大寫字母表示，將模糊命題轉化成取值在[0 ，1]范圍內的變量，其稱之為模糊命題變量，通常用小寫字母表示。設模糊命題X和Y，對應的真值分別為x=μA(X)和y=μA(Y)，則x，y∈[0，1]，

模糊命題的幾種常見運算如下［9］：

1）X∧Y的真值x∧y=min(x，y)；

2）X∨Y的真值x∨y=max(x，y)；

4）X→Y的真值x→y=xˉ∨y。

2.3 模糊推理

模糊推理［10］是指在確定的模糊規則下，由已知的模糊命題推理出新的模糊命題的一個過程，模糊推理常用“If…，then…”形式，其中“If…”部分是前提，“then…”部分是結論。主要有廣義前向推理和廣義反向推理兩種，廣義前向推理是已知前提求結論，廣義反向推理是已知結論求前提。

模糊推理的具體過程有以下步驟［11］：

1）模糊化。將輸入量進行模糊化處理，換句話說就是將輸入量轉換成模糊集合，并求得隸屬函數相對應模糊集合的隸屬度，此步驟的模糊化主要分為非單值模糊化和單值模糊化兩種方式。

2）規則庫。是若干模糊控制規則的集合，大多以“if…then…”形式進行模糊條件判斷，規則庫主要是根據研究對象特征和相關領域內專家經驗總結而成，對于一個已知規則的模糊條件可用模糊算子表示得到一個數值，數值表示模糊條件對于規則的匹配結果。

3）推理機。對每個規則賦予一個權值來進行模糊蘊涵，每個規則的蘊涵過程是給定一個單值作為輸入，輸出是一個模糊集合。

4）去模糊化。將聚類輸出的模糊集作為輸入，輸出是一單值。

其推理過程如圖1所示。

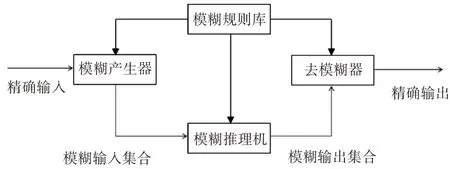
圖1 模糊推理系統

3 模糊BP神經網絡

模糊BP神經網絡［12］是將模糊系統和BP神經網絡系統有機結合的算法模型，這一模型同時兼具模糊系統知識結構表達能力和BP神經網絡系統的自學適應性能力，目前這一算法在數據預測、綜合評價、智能控制方面得到很好的應用。

模糊BP神經網絡是在BP神經網絡的結構基礎上，將輸入、輸出、權值和學習算法等因素模糊化，將傳遞函數用模糊算子來代替，將“領域知識”用模糊集合來表示。模糊系統和BP神經網絡具備一定關聯性，原理基礎是二者都是有基本神經元構成，拓撲結構相似，在理論上模糊系統能以任意精度逼近一個非線性函數，BP神經網絡具有很強的映射能力，通過反復訓練也能滿足擬合精度要求，模糊系統可以處理顯性邏輯問題，二者主要區別就是對網絡結構中各項參數的描述不同。

模糊BP神經網絡建立的設計思想是將模糊系統中的模糊化處理、模糊推理過程中模糊規則和隸屬函數用神經網絡來表示，利用神經網絡算法提高模糊系統精度。模糊神經網絡可以說是一種改進型神經網絡，在具有自學自適應功能的同時，也具備了模糊推理功能，從而進一步增強了神經網絡的透明度和解釋能力。在構建模糊神經網絡前，對各層節點的確定和優化十分重要。第一層輸入層節點數是由研究對象系統的輸出數，設節點數為m；第二層模糊化層、第三層規則層和第四層歸一化層的節點數一致，設為n；五層是輸出層。

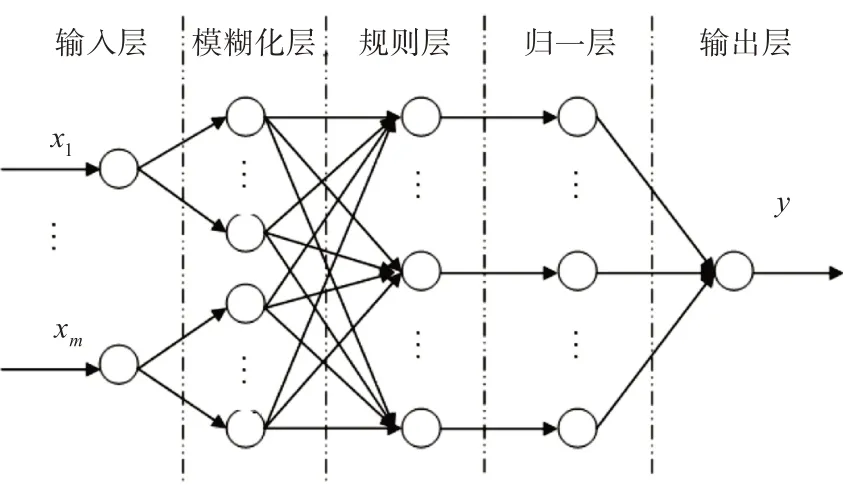
圖2 模糊BP神經網絡模型

第一層：輸入層。節點直接與輸入變量相連并由輸入層輸至下層，可表示為

第二層：模糊化層。模糊化層的作用是將輸入層的輸入變量模糊化，然后再定義模糊子集，通過各模糊子集的隸屬函數，將輸入變量轉化成對應模糊子集的隸屬度［13］，下面隸屬函數用高斯函數來表示。

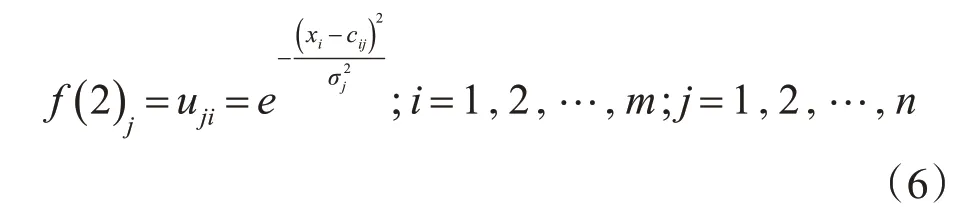
其中cij表示第i輸入節點模糊化層中第j個模糊子集隸屬函數的中心值，σj是模糊化層第j個模糊子集隸屬函數的寬度。

第三層：規則層。該層的輸出為各節點所有輸入信號的乘積，即規則層是用于匹配模糊化處理過的數據和模糊規則。

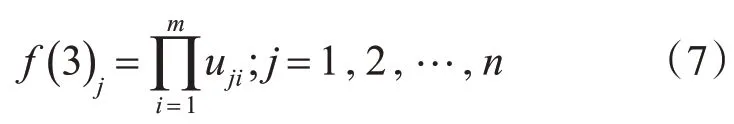
第四層：歸一層。將每個規則層輸出的模糊子集歸一化處理成一個單獨的模糊集。

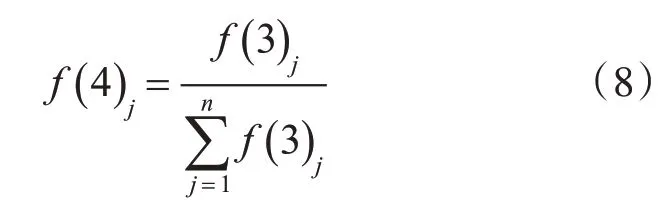
第五層：輸出層。將規則層的輸出進行反模糊處理，最后得到整個模型的輸出值。

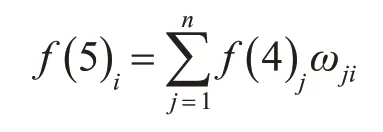
其中ωji是歸一層到輸出層各模糊集合模糊集合的連接權值。

對于模糊BP神經網絡模型，利用BP神經網絡對模糊隸屬函數的參數cij、σj和輸出層連接權值ωji進行訓練調節，以達到逼近模型輸入輸出明確的函數關系的目的。設模型的期望輸出為Fj，實際輸出為oj，模型的輸出函數記作Ej，則可得到如下關系式：

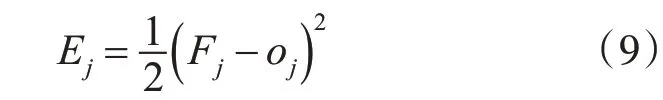
則上述三個參數的調整為

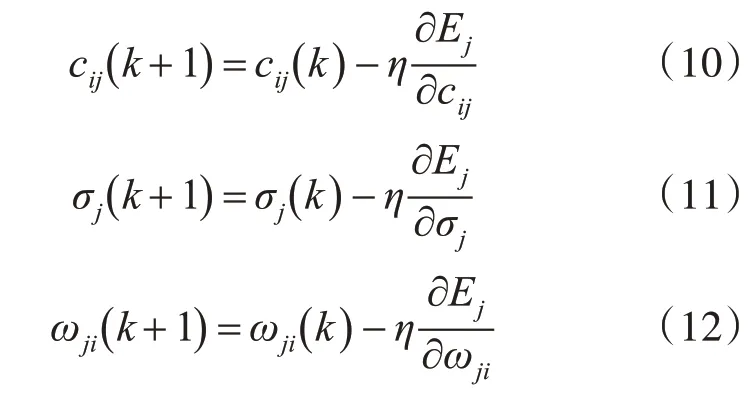
其中η是學習率，i=1，2，…，m;j=1，2，…，n。

4 模糊BP神經網絡的改進

利用BP神經網絡在反向轉播過程中利用誤差不斷修正連接權值閾值的功能，對模糊隸屬函數的參數cij、σj和輸出層連接權值ωji進行調節。

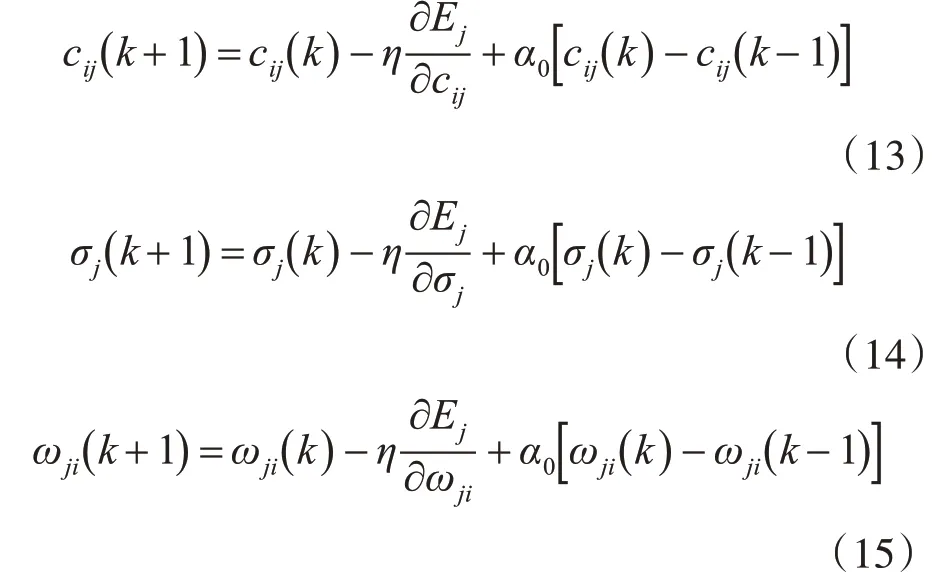
與常規權值調整公式中常數項動量因子α0不同，改進后的動量因子是一個變量，其取值受前面輸出誤差的影響，且大小隨輸出誤差比值大小做調整。按照經驗可知，α0∈( )0，1，誤差調整總體呈下降趨勢。現令

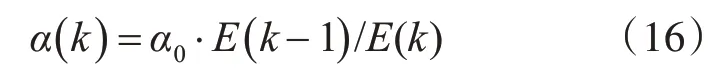
則參數cij、σj和ωji調整為

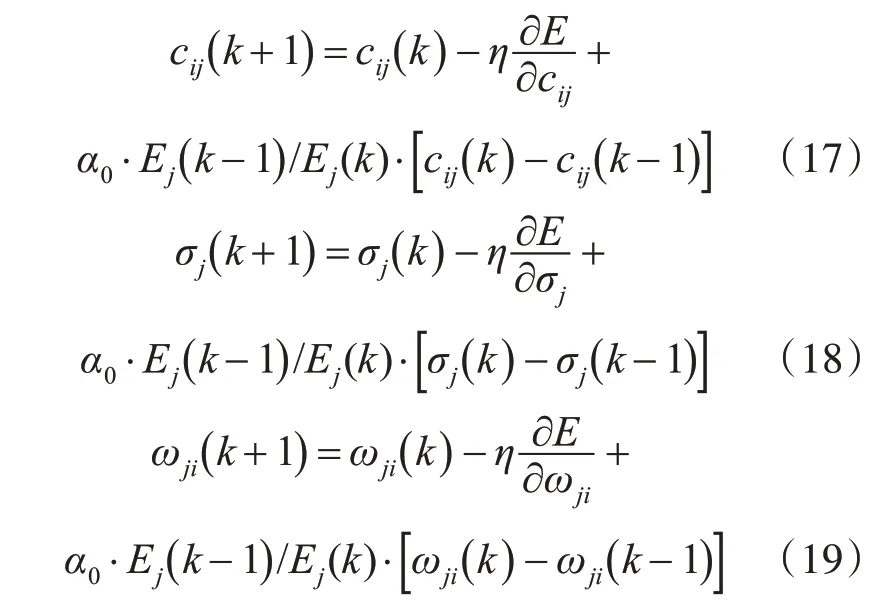
此外，學習速率η的取值對網絡的訓練性能也同樣有一定影響，通常為一常數。η取值過小，會延長訓練時間，訓練收斂減慢；η取值過大，對網絡穩定性降低起一定作用。綜合考慮訓練時間和穩定性兩方面因素，參照預先設定的誤差參數，提出對η取值進行調整，當網絡輸出誤差較上一層輸出超出設定值，則減小η值，反之增加，直至網絡訓練收斂達到預期。η取值如下：

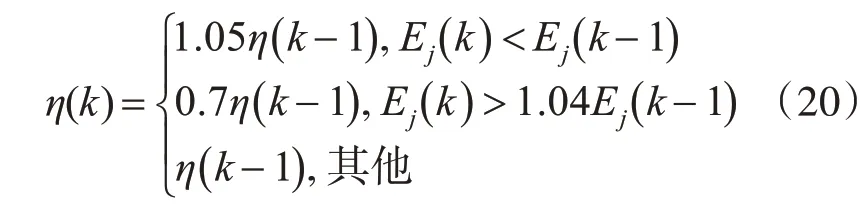
通過自動調整η來實現始終以最大允許速率對網絡進行訓練。

5 實例應用

某型防空導彈系統是目前我國正在服役的主要防空武器系統之一，具有精度高、覆蓋面廣和機動性強等特點。該型導彈雷達導引頭是整個導彈的重要部件，其工作性能的好壞直接影響整個導彈的戰斗效能。導引頭故障發生有多種影響因素導致，這些因素和故障的發生很難有明確的數學表達式來表示，故障和影響因素之間往往呈現模糊性和隨機性特征。

導引頭的性能檢測主要是電測檢測，主要檢測對象是導引頭各部件，所測量參數主要選擇磁流管電流、電源電壓、自動功率調節值、跟蹤性能參數，用四個性能參數來進行導引頭性能狀態的評價。下面根據2013~2017年各季度對該型雷達導引頭的各項性能參數測試數據來對導引頭2018年性能狀態進行預測評價。

1）輸入層參數

記輸入層各參數集合磁流管電流I、電源電壓U、自動功率調節值P、跟蹤性能參數Q。

將各測量參數進行歸一化處理：

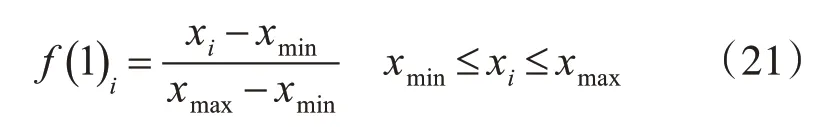
其中xmax和xmin分別代表四個檢測參數在相應指標取值范圍內的最大值和最小值。則各參數輸入在[0，1]區間取值。

2）隸屬函數選取

每個輸入量都有各自的隸屬函數，并產生多個模糊規則，三角型隸屬函數適用于解決線性問題，但導引頭故障發生多數屬于累計失效，呈非線性函數關系，將各輸入量對應的隸屬函數選擇為高斯隸屬函數。

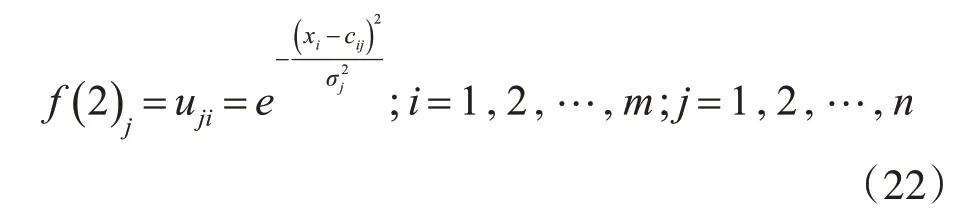
3）模型建立及訓練

按照四項指標參數變化情況對導引頭整體性能狀態影響大小來對四項指標進行權重賦值，根據經驗數據總結，四個參數權重取值分別為0.29、0.19、0.30、0.22，將各性能參數加權后生成導引頭性能完好率作為模糊BP神經網絡的輸出。根據導引頭被測性能參數特點，確定模型輸入節點數為4，輸出節點數為1，中間層節點的選擇對網絡精度和由經驗公式（r取1～10）可得，中間層節點數選7。設網絡訓練次數為1500，訓練目標0.0001，各參數權值wji的初始取值分別為0.29，0.0152，將訓練輸出與實際數據作對比，當誤差在允許范圍內，則訓練結束，否則不斷調整隸屬函數參數，直至達到理想輸出。下面利用實測數據對改進前后模型進行訓練，并對比兩模型訓練收斂速率大小。

由圖3可見，改進后的模糊BP神經網絡訓練速率要比傳統模糊BP神經網絡快。

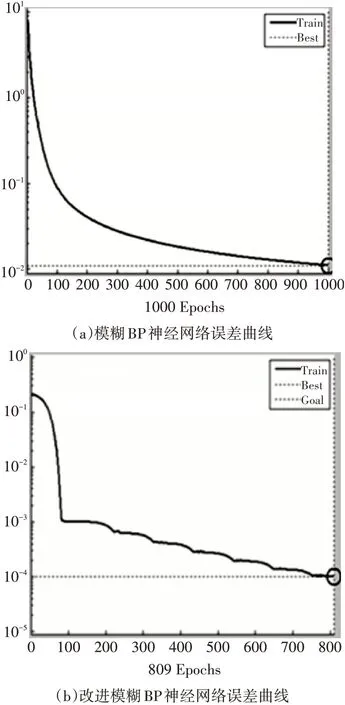
圖3 改進前后模糊BP神經網絡訓練收斂速率曲線

4）導引頭性能狀態的預測

利用改進模糊BP神經網絡對隸屬函數各參數進行調整訓練。觀察改進前后模糊BP神經網絡的運算速度和預測精度，對2018年導引頭性能狀態預測見表2。

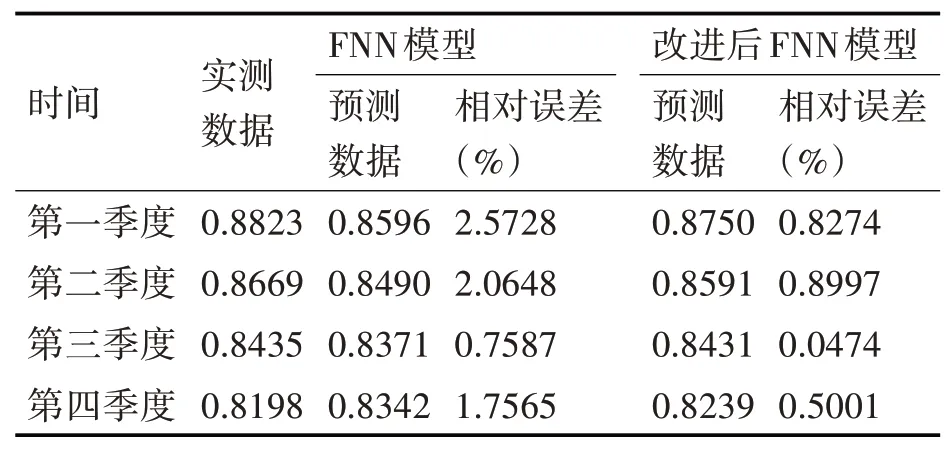
表2 改進前后FNN模型預測數據及誤差表

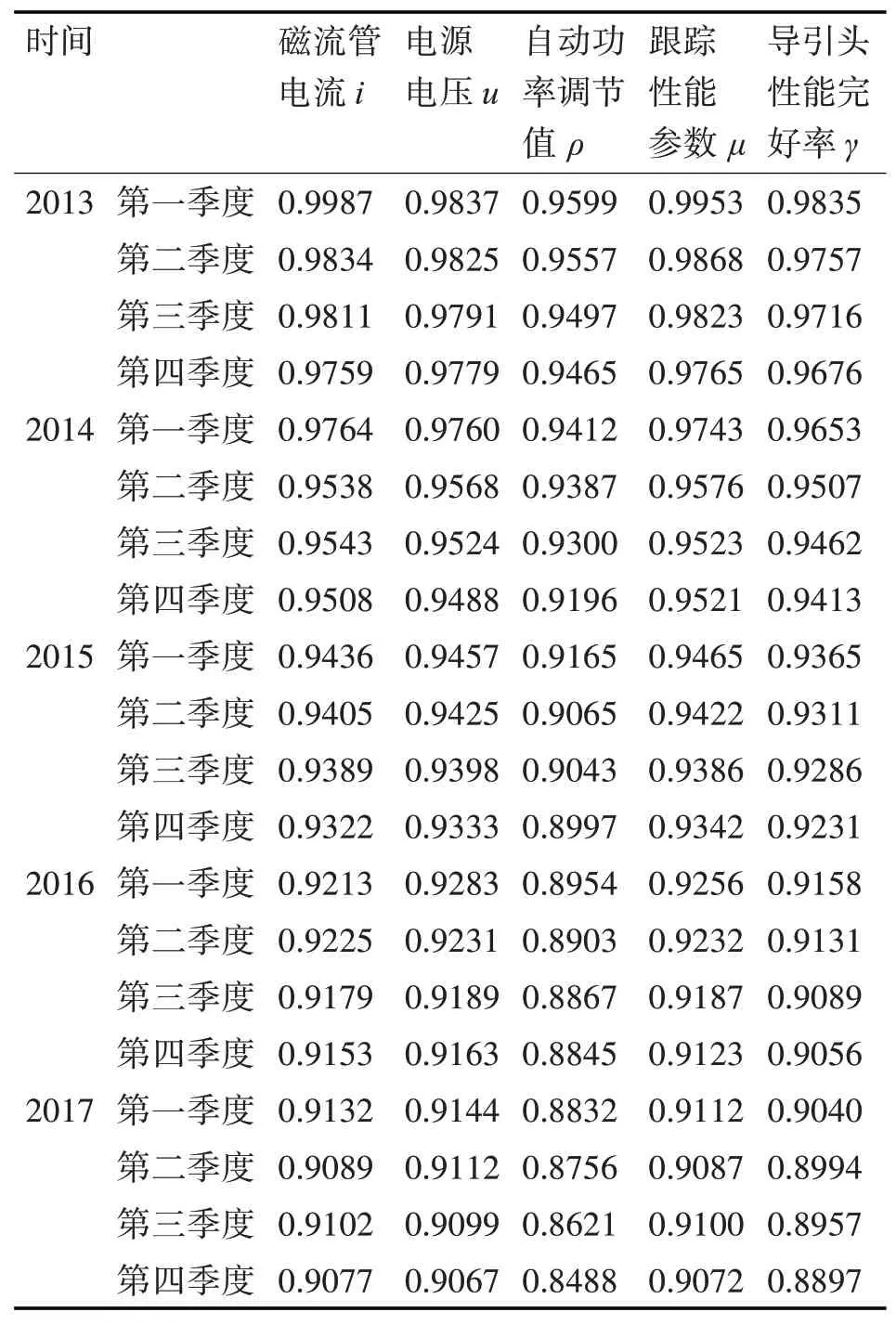
表1 導引頭各參數實測數據及性能評價表（2013年~2017年）

由圖3和表2可見，改進后的模糊BP神經網絡在運算速率和預測誤差都比改進前的模型有一定程度的提高，說明改進后模糊BP神經網絡在導引頭性能狀態預測方面有更好的適用。但是從效果上來看，運算速率和預測精度的改進效果都不太明顯，這可能取決于模糊推理系統和BP神經網絡的融合程度，需要進一步論證。

6 結語

本文在傳統模糊系統和BP神經網絡的基礎上將兩種算法結合成新的組合模型，并在組合模型的基礎上，通過調整BP神經網絡結構中的動量因子和學習速率的重新賦值來調整模糊系統中隸屬函數的取值。改進后的模糊BP神經網絡模型兼具兩種算法的優點，且在理論上收斂速度更快，運算精度更高。根據雷達導引頭性能評價實測數據，通過運算仿真實驗表明，改進后的模糊BP神經網絡訓練收斂速率更快，誤差精度也有一定程度的提高，從而證明改進模糊BP神經網絡模型對導引頭性能狀態評價具有很好的適用性。