小型對置式直線壓縮機模擬及實驗研究

洪昊 趙志康 陳曦 何韓軍

摘要：直線壓縮機具有體積小、摩擦力小、效率高以及無油潤滑等優點，其小型化設計在微電子冷卻及微型空調領域具有重要的發展前景。利用Ansoft Maxwell 有限元分析軟件建立了動磁式直線電機模型，確定了諧振工況下直線電機結構及性能參數，通過數值積分分析了空載和負載工況下的活塞位移。根據理論分析和模擬，研制了對置式直線壓縮機實驗樣機，壓縮機總質量為1.2 kg，總長度為118 mm。實驗結果顯示：以 R134a 為制冷劑時，在冷凝壓力為0.79 MPa、蒸發壓力為0.39 MPa 下，制冷量為57.3 W。模擬及實驗結果對直線壓縮機小型化設計具有參考價值。

關鍵詞：直線壓縮機;動磁式直線電機;有限元分析; R134a

中圖分類號： TF457??? 文獻標志碼： A

Simulation and experimental research on small opposed linear compressor

HONG Hao，ZHAO Zhikang，CHEN Xi，HE Hanjun

（School of Energy and Power Engineering， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract：Linear compressor has the advantages of small volume， small friction， high efficiency， and oil-free lubrication. Its miniaturization design is promising in the fields of microelectronic cooling and micro air-conditioning. A moving-magnet motor model was developed by the finite element analysis software of Ansoft Maxwell， by which the structure of the linear motor and performance under resonance conditions were determined. And the piston displacement under no- load and load conditions was analyzed by numerical integration. The experimental prototype of opposed linear compressor was developed based on the theoretical simulation. The compressor mass? was 1.2 kg? and? its? length? was 118 mm. The? experimental? results? showed? that? when evaporation pressure and condensation pressure were 0.39 MPa and 0.79 MPa， respectively with R134a? as? refrigerant，? the? cooling? capacity? of this? system? was 57.3 W. The? simulation? and experimental results can provide references for the miniaturization design of linear compressor.

Keywords：linear compressor; moving-magnet linear motor; finite element analysis; R134a

壓縮機是蒸氣壓縮制冷系統的核心部件，它決定整個制冷系統的制冷量及性能優劣。目前，市場上的制冷設備大多采用傳統往復式壓縮機。該類型壓縮機技術相對成熟，加工成本較低，但其內部的曲柄連桿機構導致壓縮機整體系統結構龐大，同時在動力傳遞過程中，各部件間相互摩擦，造成傳動效率降低、可靠性下降以及噪音與振動較大等不良影響。直線壓縮機由直線電機直接驅動活塞運動，結構緊湊，無曲柄連桿機構，采用間隙密封技術實現了無油潤滑，可替代往復式壓縮機以提高制冷系統制冷性能和效率[1–3]。

直線電機小型化及其模擬設計是目前直線壓縮機一個重要研究方向，關系到直線壓縮機在航空航天、微電子、民用制冷設備等領域的應用與發展。 Bradshaw 等[4]為了測試線性壓縮機適用于電子冷卻的可行性，研發了一臺小型線性壓縮機，探討了壓縮機幾何形狀變化的敏感性，指出泄漏間隙和活塞偏心為線性壓縮機設計時須考慮的重要參數。畢研強等[5]通過數值分析求解了動磁式直線壓縮機的數學模型，得到壓縮機啟動特性以及制冷量和制冷系數隨線圈電阻、動子質量、摩擦阻尼等參數的變化情況。 Oliveira 等[6]以Embraco公司設計的“智驅”小型直線壓縮機為模型建立無油直線壓縮機的熱力學模型，通過有限體積法計算固體部件的導熱以及壓縮機殼體內的氣體流動狀況，通過模擬得到的吸氣溫度分布同實驗結果基本吻合，但一些固體部件和排氣溫度分布與實驗相比有較大差異。唐明生等[7]通過對比測量值與實驗測試值，對壓縮機動力學參數計算方法進行校正，給出了直線壓縮機動力學參數的測量方法，并在線測量動力學參數以實現直線壓縮機運行狀態的故障診斷及在線監測。

為研究小型動磁式直線壓縮機運行特性，本文對系統運行方程組進行數值求解，分析壓縮機活塞位移響應。采用Ansoft Maxwell 電磁場有限元二維瞬態場分析軟件建立動磁式直線電機模型，依據電機性能模擬結果研發對置式直線壓縮機樣機，搭建性能測試實驗臺并進行空載及負載實驗。

1理論模型及位移響應分析

動磁式直線壓縮機動子部分由永磁體、永磁體支架、板彈簧、連接件及活塞組成，其軸向剖面結構如圖1所示。板彈簧為壓縮機活塞提供徑向支撐力和軸向往復力，定子部分由內軛鐵、外軛鐵、氣缸以及線圈組成。壓縮機的工作磁場主要有兩個：一個是永磁體產生的恒定磁場，另一個是通電線圈產生的交變磁場，在兩個磁場相互作用下，電磁驅動力推動壓縮機活塞在軸向上作往復直線運動[8]。

根據法拉第電磁感應定律，在直線電機電路中產生的感應電動勢，一部分是由于磁場強度變化產生渦旋電場導致電流定向運動的感生電動勢，另一部分是永磁體在內、外軛鐵間作直線往復運動產生的動生電動勢。在線圈兩端施加交變

電壓u（t）時，根據基爾霍夫定律以及電壓平衡關系，可得到電機驅動電壓控制方程[9]，即

u（t）= iRe+ Le + K0（1）

式中：i為線圈電流， A ;Re 為線圈電阻，Ω; Le為線圈等效電感，H;K0為比推力系數，N · A-1; t為時間， s;x為活塞位移， m。

動磁式直線壓縮機機械彈簧共振系統可簡。在壓縮機運行過程中，活塞受到電機電磁力、機械阻尼力、機械彈簧力及氣體力作用，外力間的矢量關系如圖2所示，圖中：FMT（t）為電機電磁力， N ;FML（t）為機械彈簧力， N ;FAM（t）為機械阻尼力， N ; FG（t）為氣體力， N ;x.為活塞速度， m · s?1;為活塞加速度，m · s?2;m為動子質量，kg。

根據力平衡關系可得到活塞控制方程[11]，即

電機驅動電壓控制方程與活塞控制方程一同構成動磁式直線壓縮機系統運行方程組，其機械彈簧共振系統中的勢能和動能分別與動子的位移和速度相關，電磁系統中的磁能與勵磁線圈中的電流相關，故選取活塞控制方程中的i、x（t）和速度v（t）作為系統狀態變量，可得到適用于數值積分計算的系統狀態方程組[12]，即

式中：c為等效阻尼系數，包括活塞運動過程中的線性阻尼系數，N ·（m · s）-1;k為等效彈簧剛度，包括板彈簧機械彈簧剛度和氣體彈簧剛度，N · m-1。

通過求解系統狀態方程組，可得到在一定輸入電壓條件下壓縮機的活塞位移響應。方程組中已知常量參數可由式（4）得到，即式中： Wi為壓縮機指示功， J ;X為活塞振幅， m;u0為真空磁導率， H · A-1;D為永磁體與軛鐵間隙的平均直徑， m; L為軛鐵軸向長度， m; n為永磁體軸向長度， m; N 為線圈匝數;Hc為矯頑力，A · m-1;gn為內軛鐵與永磁體間隙寬度， m;gw為外軛鐵與永磁體間隙寬度， m;ω為活塞運動的角頻率，rad · s-1;w 為永磁體的寬度， m;f 為共振頻率， Hz。

求解常微分方程一般采用龍格?庫塔法（Runge?Kutta）。該方法是一種廣泛應用于工程計算的數值積分算法，其優點在于計算精度、效率較高，穩定性好。在Matlab軟件中采用龍格?庫塔法進行數值分析求解，計算參數如表1所示。

壓縮機空載時活塞不受氣體力作用，運動平衡位置不發生偏移。圖3（a）為輸入電壓有效值為6 V 時壓縮機活塞位移響應，在電機開始運行后數個周期內活塞位移逐漸增加，運動中心并未偏移，之后達到行程為9 mm 的穩定運行工況。圖3（b）為負載工況下輸入電壓有效值為23 V 時的活塞位移響應。從圖中可以看出，當壓縮機穩定運行時，活塞運動平衡位置發生偏移。分析其原因是因為活塞兩側壓差產生的額外偏置力與機械彈簧力相平衡，使活塞往復位移中點偏離活塞啟動位置。活塞偏置會造成余隙容積增大，壓縮機效率降低。為消除活塞偏置，可采用在電源輸入交變電壓上增加定額電壓的活塞行程控制方法[13]，附加電動勢產生的電磁力抵消了活塞偏置力，使活塞位移中心重新回到初始啟動位置。

2電磁場有限元分析

在Ansoft Maxwell 有限元分析軟件中建立二維模型，模擬結構參數與實驗樣機一致。電機固有頻率與驅動電源頻率相等時即為諧振，此時在最小的驅動力下活塞能夠達到最大位移。圖4為電機在100 Hz 的諧振狀態下活塞位移、電流和電磁力隨時間的變化。當電流達到峰值，電磁力也達到最大值，活塞處于平衡位置，故電流與電磁力同相位，電流與活塞位移間的相位角為90°。

動子在位移平衡位置附近所受電磁力較大，瞬時磁感應強度大，軛鐵易達到磁飽和點，從而影響壓縮機穩定運行。圖5為電機穩定運行中永磁體接近平衡位置時磁感應強度云圖，內軛鐵和外軛鐵內部最大磁感應強度低于1.5 T。模擬中選用電工純鐵作為軛鐵材料，其磁通密度在1.9 T 左右達到飽和，故整個工況下軛鐵磁通密度未飽和，磁路穩定。

3性能測試實驗與結果分析

3.1實驗系統

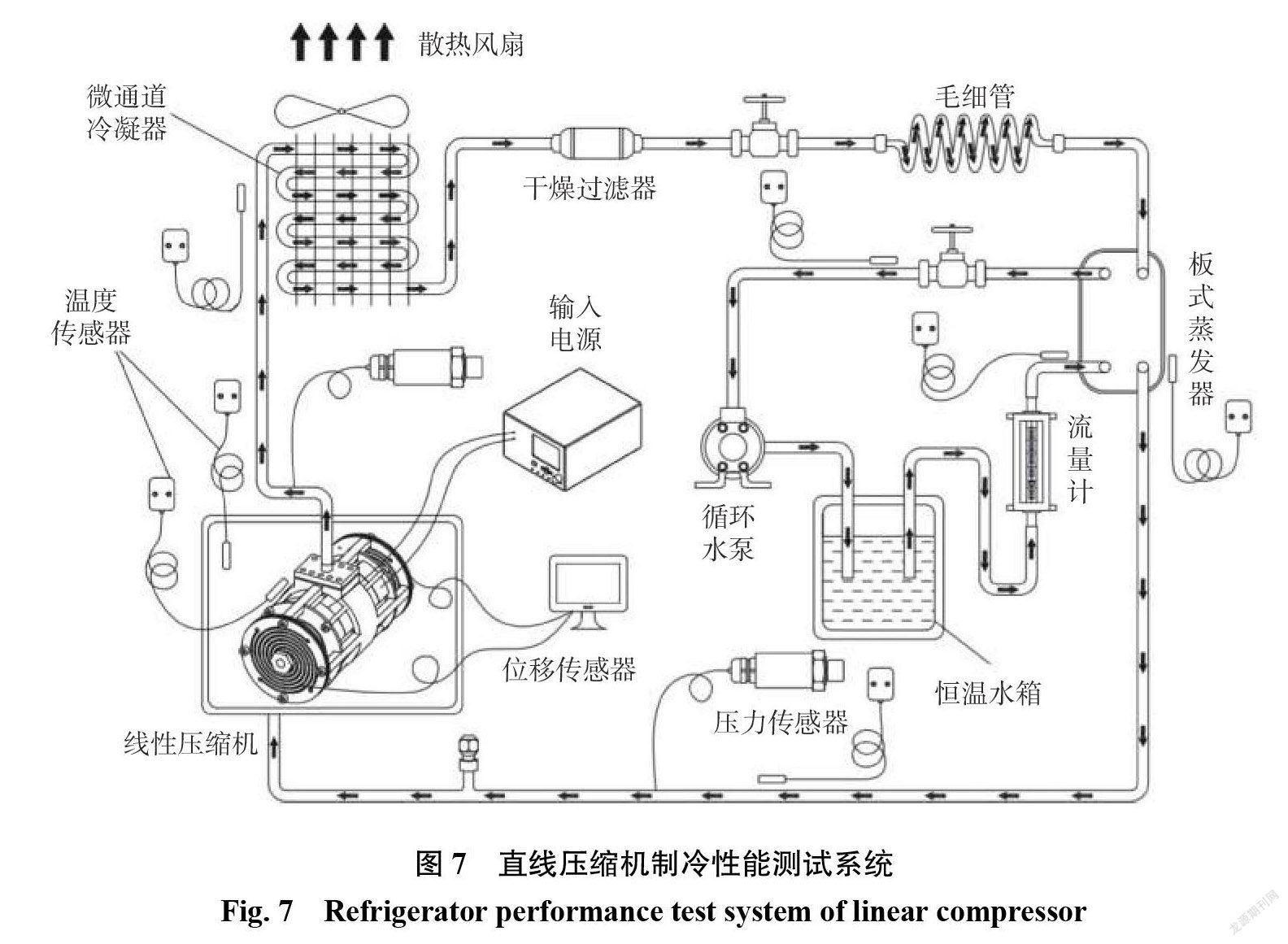
根據理論分析及電磁場有限元模擬結果開發了小型雙活塞對置式制冷壓縮機樣機，實物如圖6所示。該壓縮機整機總質量為1.2 kg，最大直徑為62 mm，長度為118 mm。實驗需測試樣機在制冷系統中的運行工況參數，包括壓縮機輸入電壓、驅動電源頻率、壓縮活塞行程、吸氣壓力、排氣壓力及制冷量等關鍵性能參數，故搭建了較完備的性能測試與參數調節系統。直線壓縮機制冷性能測試系統如圖7所示。

3.2空載特性實驗

壓縮機空載運行時理論上無氣體力作用，系統剛度僅為板彈簧機械剛度，系統共振頻率發生改變。共振頻率計算式為

圖8為空載工況下輸入電壓不變時單個直線電機活塞振幅、電機效率和輸入功率隨驅動電源頻率的變化。隨著驅動電源頻率的增加，輸入功率先減小后增大，電機效率和活塞振幅先增大后減小，在頻率為74 Hz 時，輸入功率最低，為17 W，電機效率也達到最大值，為0.82。在75 Hz 左右活塞振幅達到最大值，該頻率與電機效率最大和輸入功率最小時的頻率基本吻合，可認為壓縮機達到諧振狀態。根據共振頻率計算式得到的頻率為71 Hz，稍低于實驗共振頻率。其原因是：由于壓縮過程中吸氣、排氣閥片開啟與關閉造成活塞兩側壓力不相等，氣體彈簧發揮作用，系統剛度大于板彈簧剛度，故實驗共振頻率略大于理論計算值。

3.3負載特性實驗

圖9～11分別為制冷量，壓縮機吸氣和排氣壓力，壓縮機吸氣和排氣溫度隨運行時間的變化。由于壓縮機吸氣管道較短，過熱度小，故壓縮機吸氣溫度近似為蒸發溫度。實驗中施加了4.3 V 的偏置電壓以抵消活塞偏置造成的不利影響，并在冷凝壓力為0.79 MPa、蒸發壓力為0.39 MPa 時測得最大制冷量為57.3 W，壓縮機吸氣溫度降至7.3 C，此時的 COP 為1.15。實驗中線性壓縮機的排氣溫度持續上升導致制冷效果變差。其原因在于：電機繞組線圈電流負荷較高，發熱量較大，熱量傳遞給壓縮腔導致排氣溫度上升。通過為直線電機配置主動冷卻設備可有效控制排氣溫度。實驗結果與理論分析及模擬結果有一定差距。其原因在于：壓縮機實際機械阻尼大于電機模擬中的機械阻尼，活塞與氣缸間摩擦較嚴重，另外，壓縮腔內高壓氣體向背壓腔泄漏導致壓比降低。該不良影響主要由兩方面原因造成：吸氣、排氣閥片延遲開啟和閉合，導致氣體回流，排氣壓力減小，背壓腔壓力升高;活塞磨損與偏置導致活塞與氣缸之間間隙變大，間隙密封效果變差。

4結論

為研究小型動磁式直線壓縮機的制冷性能，開發并搭建了直線壓縮機制冷性能測試系統。測試了小型對置式直線壓縮機空載和負載工況下的直線電機性能，電機達到諧振狀態時活塞振幅與電機效率最大，輸入功率最小。負載實驗結果表明，在冷凝壓力為0.79 MPa、蒸發壓力為0.39 MPa 時，制冷溫度為7.3 C，COP 為1.15，系統制冷量為57.3 W。

參考文獻：

[1]邰曉亮.動磁式直線電機驅動微小型活塞壓縮機理論分析及實驗研究[D].上海：上海交通大學， 2009.

[2] LIANG K， STONE R， DADD M， et al. A novel linearelectromagnetic-drive? oil-free? refrigeration? compressorusing R134a[J]. International? Journal? of? Refrigeration，2014， 40：450-459.

[3] 陳曦， 張華， 吳亦農， 等.200 K/40 W 自由活塞斯特林制冷機的實驗研究[J].上海理工大學學報 ， 2007， 29（4）：337-344.

[4] BRADSHAW C R， GROLL E A， GARIMELLA S V.Acomprehensive? model? of? a? miniature-scale? linear compressor? for? electronics? cooling[J]. International Journal of Refrigeration， 2011， 34（1）：63-73.

[5] 畢研強， 徐向華， 梁新剛.動磁式直線壓縮機對制冷量與 COP 影響分析[J].清華大學學報：自然科學版 ， 2014， 54（7）：884-890.

[6] OLIVEIRA? M? J，? DINIZ? M? C，? DESCHAMPS? C? J.Thermal modelling and analysis of an oil-free linear compressor[C]//Proceedings? of? the 9th? International Conference on Compressors and their Systems. London， UK： IOP， 2015：012016.

[7] 唐明生， 鄒慧明， 王敏， 等.動力學參數在直線壓縮機故障診斷中的應用[J].壓縮機技術， 2019（3）：21-25，32.

[8] 謝潔飛， 金濤， 童水光.直線壓縮機的研究現狀與發展趨勢[J].流體機械， 2004， 32（12）：31-35.

[9] 雷美珍， 王立強， 夏永明.動磁式雙定子直線壓縮機動態特性仿真研究[J].低溫與超導， 2018， 46（1）：7-11，35.

[10]張博.基于動磁式直線振蕩電機的直線縮機技術的研究[D].南京：南京理工大學， 2015.

[11]鄧偉峰.大功率動磁式線性壓縮機關鍵技術與實驗研究[D].上海：中國科學院研究生院（上海技術物理研究所）， 2016.

[12]謝潔飛.動磁式直線壓縮機理論與試驗研究[D].杭州：浙江大學， 2005.

[13]崔麗娜.直線壓縮機控制系統的開發[D].杭州：浙江大學， 2005.