基于Matlab的熱網換熱站最短分布問題研究

常世杰 袁銘潤

(佳木斯大學信息電子技術學院，黑龍江 佳木斯 154007)

0 引言

伴隨著我國經濟的飛速發展與科技水平的提高，人民生活水平得到顯著改善，針對于改善民生問題，熱網可以有效解決人民冬季冷暖問題，使人民不再飽受冬季寒冷之苦，在改善人民生活中的作用不可小覷。伴隨著熱網需求的不斷增多與可持續發展戰略的不斷推進，加快熱網基礎建設的同時，更要做到清潔供暖，節能減排。既要溫暖過冬，又要藍天白云，將黨和政府對人民的關懷“干凈”地送到千家萬戶，是供熱企業所共同奮斗的目標。

要將熱網做到“清潔、安全、高效、節能”四個方面，供暖方式的選擇，能源結構的調整不可忽略，但是熱網分布更為重要。優化熱網分布路徑，降低不必要的冗余熱網分布，縮短熱網管網輸送距離，可有效改善熱網因輸熱管距離較長導致熱量散失過多的問題，從本質上提高熱網運行效率，同時降低熱網管網鋪設中能源設施消耗問題，減少熱網鋪設工作量，大幅度降低熱網投運成本，減少不必要的經濟損失。

1 熱網換熱站分布模型建立

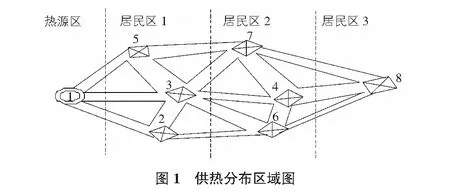
在實際生活中，熱網換熱站的分布需經現場實地考察，測量以及地形分析，繪制出熱網換熱站擬分布圖形與方案，根據不同熱網換熱站節點位置與傳輸距離，篩選出較短的熱網路線，盡可能減小熱網在管網輸送載熱體中因傳輸距離導致的熱量散失。假設通過現場測量與數據分析，得到如圖1所示的供熱區域圖。其中熱源為火力發電廠，位于居民住宅區的邊緣，每個居民區都應分布至少1個換熱站，居民區1的換熱站預設方案為2,3,5，居民區2的換熱站預設方案為6,4,7，居民區3的換熱站出于地形分布問題只能設置在8的位置。

熱源與換熱站間，換熱站與換熱站間的距離如表1所示。其中換熱站間距離單位為km，換熱站間無直接距離時為“—”。例如：熱源1到熱源1的距離為0，換熱站2到換熱站3間的距離為3 km，換熱站3到換熱站4間的距離為—，即沒有直接通路。

表1 熱網換熱站分布距離(預設方案)表

通過實際模型簡化，應用圖論簡化實際熱網分布，將換熱站簡化成每一個帶標號的節點，其中節點1為熱源，節點2,3,4,5,6,7,8代表換熱站2,3,4,5,6,7,8，簡化后熱網換熱站分布模型圖如圖2所示。現需以熱源1為起始點，流經居民區1中的換熱站(2/3/5)，再過居民區2中的換熱站(6/4/7)，最后到達居民區3，換熱站8為終止點，要通過應用計算機輔助設計，規劃出熱網換熱站分布最短路線。

2 Matlab輔助設計

通過應用計算機輔助設計軟件Matlab對熱網換熱站分布進行輔助設計，該問題可簡化成G(V(G),E(G))，其中V(G)代表圖論節點集;E(G)代表圖論邊長集，或權重集。通過應用graph函數繪制G的圖像，graph(s,t,w)表示從節點s到極點t以w的權重創建邊，并在Matlab中繪制該圖像。Matlab程序如下：

>>s=[1 1 1 2 2 3 3 3 3 4 4 4 5 6 7];

t=[5 3 2 3 6 5 7 4 6 7 8 6 7 8 8];

w=[6 4 8 3 5 4 6 7 3 8 3 2 2 4 3];

G=graph(s,t,w);

plot(G,′EdgeLabel′,G.Edges.Weight,′linewidth′,2)

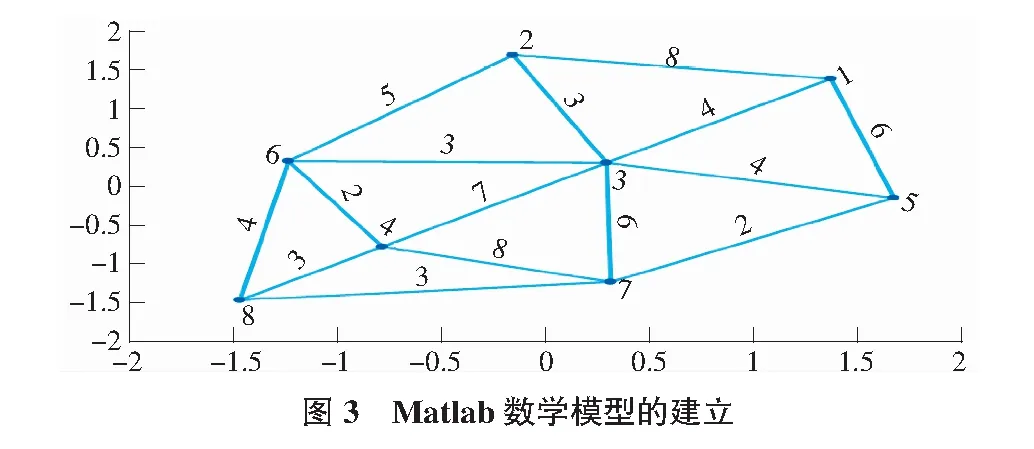
Matlab程序所繪制的熱網分布圖像如圖3所示。通過將該圖與圖2對比可得，兩者間差異不大，可全面的表示出各個換熱站節點與換熱站間距離，保證了下一步計算機輔助分析的不失真。

現要在節點1～節點8之間尋求一最短路徑，用來建立換熱站以及熱網的鋪設。通過應用[P,d]=shortestpath(G,start,end[,′Method′,algorithm])函數，其中G為graph函數，start為起始熱源1，end為終止換熱站8，[,′Method′,algorithm]為最短路徑的求取方法，此處采用迪杰斯特拉Dijkstra算法，P為熱網分布最短路徑經過的換熱站站點，d為最短路徑換熱站間的距離。Matlab程序如下：

>> clc,clear

s=[1 1 1 2 2 3 3 3 3 4 4 4 5 6 7];

t=[5 3 2 3 6 5 7 4 6 7 8 6 7 8 8];

w=[6 4 8 3 5 4 6 7 3 8 3 2 2 4 3];

G=graph(s,t,w);

[P,d]=shortestpath(G, 1, 8);

plot=plot(G, ′EdgeLabel′, G.Edges.Weight, ′linewidth′, 2);

highlight(plot, P, ′EdgeColor′, ′r′)

Matlab程序運行結果如圖4所示，求取最短路為節點1到節點3，再到節點6最后終止于節點8，此時熱網一次管網鋪設總距離為8 km，換熱站分別為3號換熱站，6號換熱站和8號換熱站，分別覆蓋三個居民區，在預設方案路徑中，該路徑所需鋪設管網最短，熱量在傳輸中的損失最少，大幅提升能源利用率，同時降低供熱工程所需材料設備，滿足設計要求。

3 設計校驗分析

在城市熱網鋪設時，往往會涉及到城鎮與城鎮之間，換熱站與熱源之間，換熱站與換熱站之間的路徑分布問題，從多條支路方案中篩選出距離相對較近的路線，是整個熱網換熱站分布的核心。通過應用迪杰斯特拉算法確定熱網最短分布路線，迪杰斯特拉算法是目前在生活中針對分布規劃，最優路徑的選取等問題應用較多的一種算法，例如：鐵路物資調配問題，城市軌道交通路線鋪設問題，公交車站分布問題等，該算法的核心思想是以起始點為中心向外廣度優先搜索至終點，從而尋找到從指定的起始點到指定的終止點間的最短路徑。應用該算法將換熱站與熱源作為節點，預選方案路線距離作為參考，實現最短路徑選取。

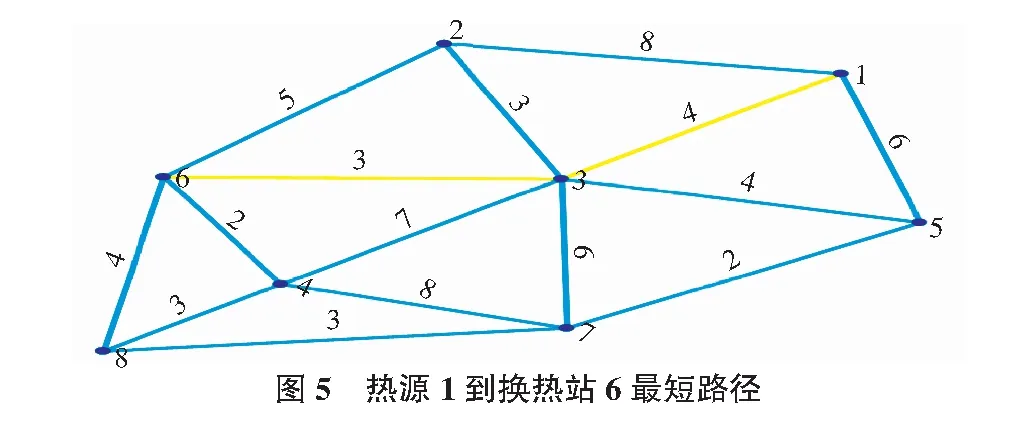
通過上述Matlab程序設計及結果分析，在該熱網分布預設方案中，在諸多組合方案中選出最短路徑方案，該方案為熱源1到終點換熱站8的最短路徑，同時針對于路徑上所經過的換熱站3和6，該路徑仍是熱源1到換熱站3和6的最短路徑，即該路徑上所經過的換熱站到熱源1的距離也是最短的。例：從熱源1到換熱站3的方案有：1—3(4 km)，1—2—3(11 km)，1—5—3(10 km)，從熱源1到換熱站6之間的最短路徑如圖5所示。相比較而言仍是該路徑上的方案距離最短。同時，應用計算機輔助設計熱網分布，工作效率有較大提升，在面臨較多數據與多種預設方案時，可通過計算機代替人工進行繁雜計算，從而挑選出較優的預設方案，實際熱網鋪設工程中仍需考慮較多外界因素。

4 結語

通過應用Matlab建立熱網分布優化數學模型，借助計算機強大的計算能力，應用迪杰斯特拉Dijkstra算法在諸多預設熱網方案中選出最優路徑，同時可推廣至較多預設方案的分析縮短熱網鋪設距離，可以有效降低熱網架設中的成本，降低熱網維護工作人員的任務量，同時減少熱網傳輸過程中的熱量損失，從根本上解決熱量散失與傳輸距離的矛盾問題，提升能源利用率，可為供熱帶來較高的經濟效益與社會效益，具有較高的實用性。