電磁發射打擊精度計算方法分析

唐曉燕，連海根，余俊松，杜 雪

（1.中國電子科技集團公司第二十七研究所，河南 鄭州 450047；2.陸軍裝備部駐西安地區軍事代表局駐鄭州地區軍事代表室，河南 鄭州 450047）

武器系統的效能評估是武器研制過程中十分重要的一個問題。射擊精度是衡量武器系統能否命中目標的一個重要戰技指標，精確打擊是現代兵器發展的最終追求目標。射擊精度的估計與評定一直受到武器研制和鑒定部門的關注。射擊精度包括射擊準確度和射擊密集度，前者描述了落點的系統性偏差，后者描述了落點的隨機散布特性。

電磁軌道炮發射彈丸的速度突破了普通火炮的性能極限，彈丸具有重大的動能，大大增強了對目標的毀傷能力，同時減小了彈丸到達目標的飛行時間，增加了對付快速目標的有效性和命中率，電磁軌道炮視為未來防空作戰中的重要備選武器之一，電磁軌道炮精確打擊在電磁軌道炮研究領域具有非常重要的地位。

1 射向散布定義

在相同條件下，向同一目標發射出多枚射彈，由于多種因素的影響，射彈的彈著點將在目標附近形成散布，其平均彈著點（散布中心）到瞄準點（一般為目標中心）的距離稱為炮彈的系統誤差，每個彈著點到平均彈著點的距離稱為隨機誤差，亦稱散布度。通常系統誤差比隨機誤差小并可以修正，因此又近似地把瞄準點作為平均彈著點。

電磁發射系統的系統誤差主要包括發射系統集成裝配誤差、膛口抖動誤差等。隨機誤差主要包括膛口抖動和電弧力作用誤差等。

對于電磁軌道炮，系統誤差可以通過標校進行修正，本文通過電磁軌道炮的打擊精度重點考慮射擊密集度情況，即射向散布情況。通過對不同的射向散布計算方法進行對比分析，尋找適合的射擊精度評估方法。

2 射向散布計算方法

武器系統射擊精度的估計方法有許多種，火炮、輕武器、地地戰略導彈等武器系統常用圓概率誤差CEP50的計算方法進行效能評估，本文根據CEP50的計算方法給出相應的CEP70、CEP80計算公式，同時提出最大包絡法、高速射像質心法和圖解法這三種新的射向散布計算方法，下面對上述不同散布評估方法進行介紹。

2.1 圓概率誤差法

圓概率誤差是衡量炮彈命中精度的一個尺度。計算圓概率誤差的一般方法是先測出各彈著點的坐標，求出平均彈著點的坐標，再用數學公式進行計算。對立靶目標進行射擊，以目標為中心，射擊方位方向分為橫軸，射擊高低方向分為縱軸，以（Y，Z）表示立靶靶面彈丸落點坐標，且（Y，Z）服從正態分布，縱橫向獨立。

圓概率誤差CEP：

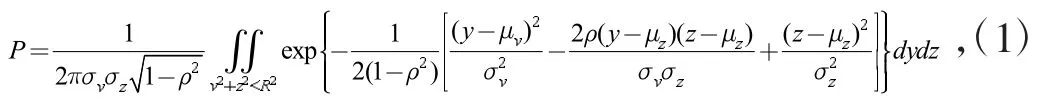
式中：σz、σy表示方向、高低散布標準差；μy、μz表示方向、高低散布均值；ρ表示高低、方向落點偏差相關系數，0≤|ρ|<1；

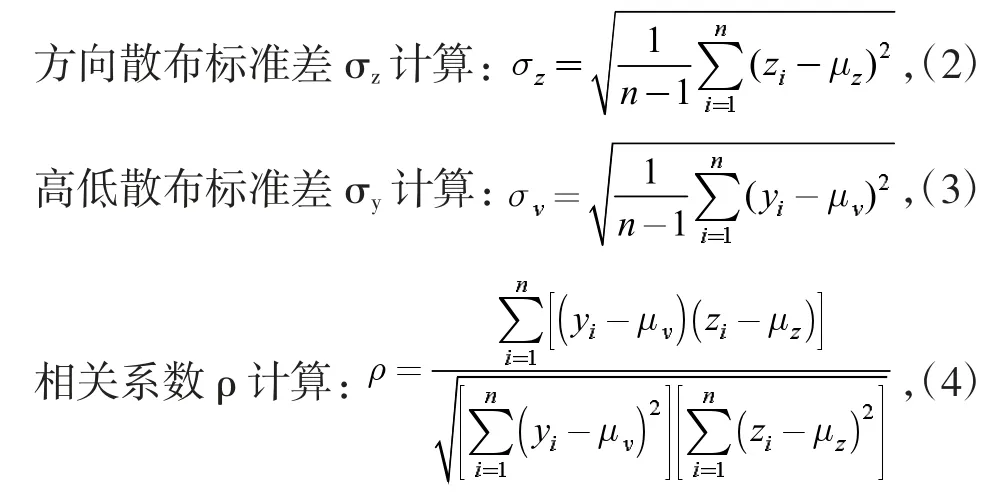
（1）CEP50計算公式如下：

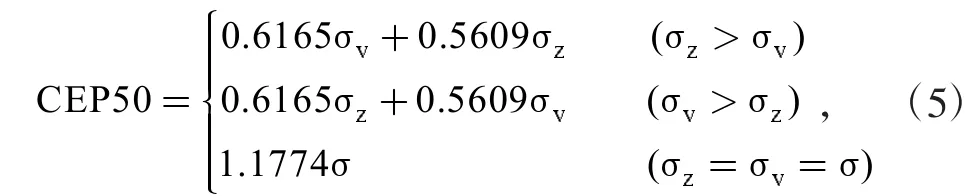
根據上述CEP50的計算過程，用同樣地計算方法，給出CEP70，CEP80的圓概率誤差計算公式。

（2）CEP70計算公式如下：

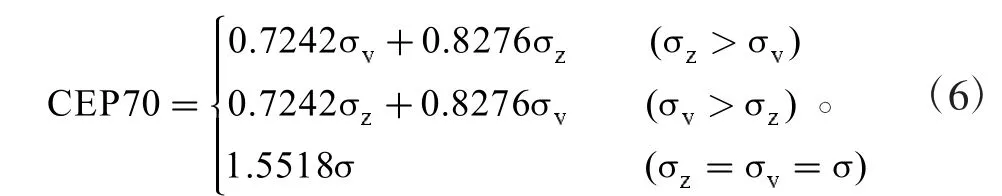
（3）CEP80計算公式如下：

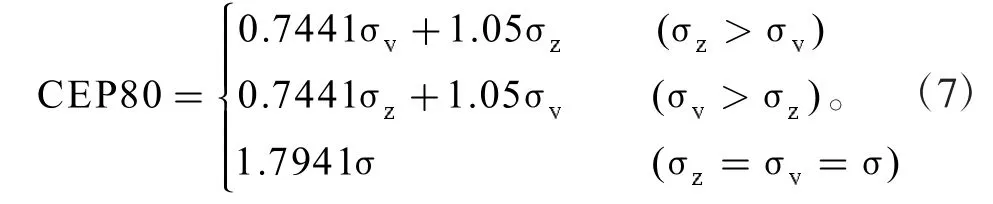
射向散布：2CEP/L（全角），L為炮口到靶心距離。

2.2 最大包絡法

根據一組試驗射彈在靶板上的彈著點最大包絡進行計算。

假設試驗最大包絡尺寸為Y*Z（Y方向為俯仰方向，Z方向為水平方向），彈長為D，炮口距離靶面垂直距離為S，η為射彈姿態有翻轉的情況，著靶后擴大彈孔采取縮減系數，則下彈著點包絡在俯仰和水平方向的射向散布分別是：

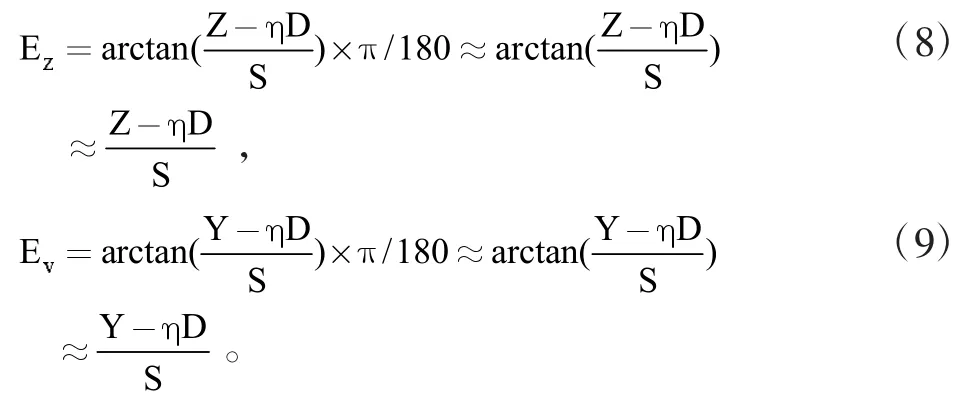
2.3 圖解法

對于圖解法，本文通過計算不同射彈落點與平均坐標點之間的距離，并將這些距離由小到大排序，這些距離可以看做是不同大小的半徑，以平均坐標為圓心，可以繪制出若干不同的圓，這些圓包含射彈落點數依次為1，2，3……，n，（n表示為試驗中發射的射彈量）。根據落點數量可計算不同圓對應的落點率，由此得到不同落點對應的射向散布精度。具體步驟如下：

（1）先測出各彈著點的坐標，（Yi，Zi）表示立靶靶面彈丸落點i（i=1、2、…、n）的俯仰、水平坐標。

（2）根據已測得彈著點坐標，計算出平均彈著點坐標，即散布中心

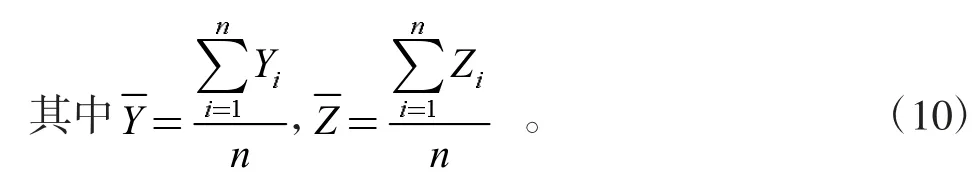
（3）計算各點的散布半徑Ri。

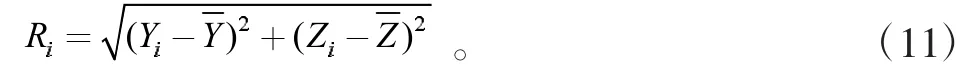
（4）對計算出的各點散布半徑進行從小到大的排序，得到R'j，其中j=1、2、…、n。

（5）繪制包絡圓，以散布中心（Y，Z）為圓心，排序后的各散布半徑R'j（j=1、2、…、n），得到的圓命名為C（j）（j=1、2、…、n），包含的落點數量分別對應1、2、3，……，n。

（6）計算對應要求落點率的射向散布精度。

a.落點率：η=j/n。

b.不同落點率對應的射向散布精度：δ=2R'j/L。

3 不同計算方法結果對比分析

某電磁發射進行若干發次模擬發射試驗，模擬試驗前約定散布要求，按照上一章節射向散布計算方法進行計算繪圖，結合落點率和散布要求進行方法對比分析。

（1）對于圓概率誤差法，圖1給出圓概率誤差CEP50、CEP70、CEP80包含射彈點數。

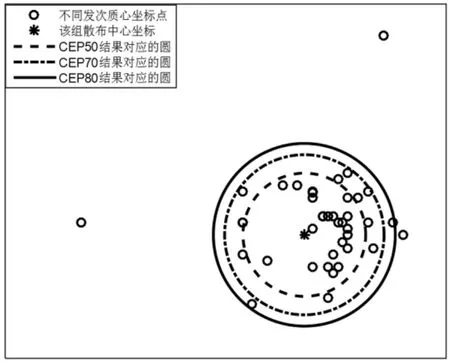
圖1 圓概率誤差法示意圖

從圖1中可看出：CEP50、CEP70、CEP80這三種圓概率誤差法通過計算公式繪圖的實際落點率要遠遠高于計算公式對應的落點率，這是由于圓概率誤差計算方法適用于試驗數據較大情形，在試驗數據較小的情況下圓概率誤差方法將不適用。

（2）對于圖解法，根據不同落點率要求進行畫圓，獲取足夠數量的落點以滿足不同落點率要求。圖2給出采用圖解法繪制的圓圖，不同的圓包含不同的射彈落點情況。

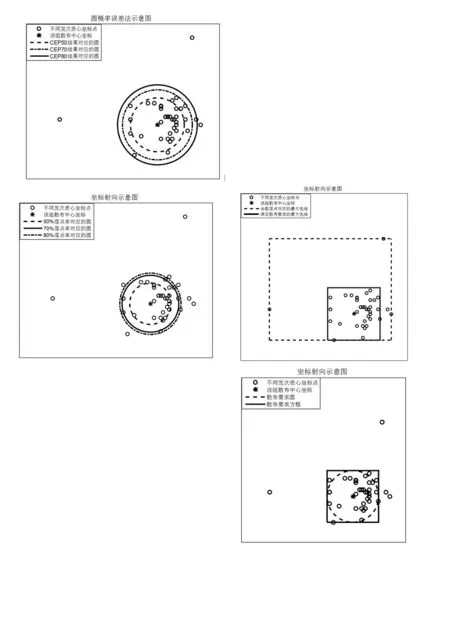
圖2 圖解法畫圓示意圖

從圖2中可看出不同圓中的落點率與實際要求完全一致。

（3）對于最大包絡法，可以快速計算出射向散布結果，且包含全數落點，但考慮全數落點會致使射向散布偏大，不滿足要求，對此可以縮小包絡，采用滿足散布要求的方框進行替代，在此方框內計算相應落點率，檢測在射向散布要求下是否滿足落點率要求。

從圖3中可以得到，在不進行全數落點統計的情況下，進行滿足散布要求的最大包絡繪制，并進行落點率統計，得出既滿足散布要求，又不低于落點率要求的最優包絡。

圖3 最大包絡示意圖

按照射向散布要求，可以將靶面繪制成圓形，也可繪制成方框形狀，圖4給出按照散布要求繪制的圖形。

從圖4中可得出以下結果：

圖4 散布要求示意圖

a.圓形和方框包絡對應的落點率不同，方框落點率要優于圓形落點率。

b.由于方框包絡面積大于圓形包絡，在滿足射向散布要求前提下，落點率情況方框優于圓形。

4 結論

四種射向散布計算分析方法，都可以有效獲得射向散布結果，不同的計算方法對指標滿足度有一定的影響。

（1）由于受到電磁動能武器壽命限制，受到試驗數據量的影響，圓概率誤差法在計算落點率結果上存在較大偏差，實際落點情況優于計算公式對應的落點率。

（2）圖解法可以有效解決圓概率誤差方法中存在的落點率不一致問題。

（3）最大包絡法可以有效計算出所有落點情況下的射向散布結果，在全數落點情況下，射向散布結果可能出現超出要求情況，對此收縮小包絡，采用滿足散布要求的方框進行替代，在此方框內計算相應落點率，檢測在射向散布要求下是否滿足落點率要求。