一種高效的SM2數字簽名批量驗證算法

阮 鷗，陳吉晨，毛 浩

(湖北工業大學計算機學院，湖北 武漢 430068)

1 引言

數字簽名常用于身份認證、抗抵賴性等方面。例如，銀行發薪資問題，假設用戶B為中國郵政銀行經理，用戶A為中國郵政集團公司(有100萬員工)的會計人員，用戶A每個月底需要把所有員工(約100萬)的薪資數據及其簽名發送給中國郵政銀行，以便用戶B將薪資轉賬給所有員工，此時用戶B需要一一驗證用戶A發送過來的每一位員工的薪資數據及其簽名，需要做100萬次驗證，產生大量的計算工作，顯著降低了銀行轉賬系統的效率，此時數字簽名批量驗證顯得尤為重要。Naccache等人[1]最早提出了批量驗證(Batch Verification)算法。批量驗證算法的基本思想是將多個簽名(可能來自不同的簽名者)組成一個新的集合，并對新的集合進行驗證。如果該集合通過驗證，則接受該集合中的所有簽名，否則，拒絕集合中所有簽名。目前，對于DSA(Digital Signature Algorithm)、RSA(Rivest, Shamir, Adleman)和ECDSA(Elliptic Curve Digital Signature Algorithm) 等數字簽名，研究者均提出了相應的批量驗證算法，其中Harn[2]針對DSA設計了一種交互式的批量驗證算法，Hwang等人[3]提出了DSA、RSA的批量驗證算法，Cheon等人[4]針對ECDSA*設計了一種快速批量驗證多個數字簽名的方案。

在數據外包、智能汽車、智能電網和物聯網等現代應用領域中，為了提高數字簽名批量驗證速度，研究者提出了不同的方案。Zhang等人[5]提出了基于外包功能的批量驗證計算方案，客戶端查詢請求數據時，由服務器進行批量身份驗證，而客戶端使用更少的時間來驗證服務器計算的正確性。Bayat等人[6]提出了一種具有批量驗證功能的安全認證方案，將批量驗證應用于車聯網中，車輛與車輛進行通信，以及車輛與固定的路邊單位或云平臺進行通信時，使用批量驗證能夠更快速地處理數據，減少事故，改善交通狀況。Guo等人[7]提出基于批量驗證輕量級隱私保護數據聚合的智能電網方案，數據聚合者能夠對加密電力數據進行批量驗證，從而提高整個系統的計算效率。Xiong等人[8]提出了一種安全高效無證書批量驗證的物聯網方案，方案中的信任模型可幫助網關節點識別受信任的傳感器節點執行批量驗證。

SM2算法[9]是我國科研人員基于ECC橢圓曲線密碼理論自主研發設計的，采用素數域256位橢圓曲線作為標準曲線生成密鑰對。在ECDSA數字簽名算法中，對待簽名消息M不做任何處理，而SM2數字簽名算法對待簽名消息M進行了處理，其中包含用戶的可辨別標識、部分橢圓曲線系統參數和用戶公鑰的雜湊值，使得安全性和抵賴性更強，因此在數字簽名方面SM2優于ECDSA、ECDH(Elliptic Curve Diffie-Hellman key exchange)等算法。目前，SM2還被應用于盲簽名[10]、代理簽名[11]、門限密碼體制[12]和安全雙方協作[13]等領域。然而，SM2的批量驗證算法還沒有人進行研究。本文針對SM2數字簽名，提出了相同簽名者與不同簽名者的批量驗證算法。

本文提出了一種安全高效的SM2批量驗證算法。算法并非在每一次簽名完之后立即驗證，而是一次同時驗證多個簽名。因為在SM2數字簽名驗證過程中，點乘運算是一項非常耗時的運算，所以本文通過減少點乘運算來縮短驗證時間，進而提高算法效率。實驗數據表明，在消息數量相同的情況下，批量驗證算法的效率遠高于單個驗證算法的效率，例如當簽名數量達到約100萬(220)時，單個驗證算法大約需要1 h，而批量驗證算法僅需2 s。

2 相關工作

1991年，美國政府提出了數字簽名標準DSS(Digital Signature Standard)作為聯邦標準，使用數字簽名算法(DSA)簽署電子文檔。DSA數字簽名算法是一種基于離散對數問題的ElGamal型簽名方案[14]，其驗證每個簽名至少需要2次模冪運算。由于模冪運算是一項非常耗時的計算，因此需要使用專用硬件或高效的軟件算法加速驗證過程。

1994年，Naccache等人[1]首次提出了一種交互式DSA批量驗證算法，同年，Lim等人[15]指出這種交互式DSA批量驗證算法是不安全的，此方案中敵手可以偽造一個簽名集合來滿足批量驗證公式。1995年，Harn[2]針對DSA數字簽名算法，設計了一種交互式的批量驗證算法，其中簽名者與驗證者交互生成n個簽名，驗證者對n個簽名進行驗證。1998年，Harn[16]再次針對DSA數字簽名算法，提出了一種非交互式的批量驗證算法，它充分利用簽名者的公鑰作為驗證紐帶，摒棄了簽名者產生簽名時需要與驗證者交互的過程。2001年，Hwang等人[17]指出文獻[16]的方案中簽名者可以偽造個人簽名，并使得錯誤的批量驗證有效。

1998年，Harn[18]針對RSA數字簽名算法，提出了一種批量驗證方案，使用相同私鑰對多個消息進行簽名，并且對多個簽名進行批量驗證。2000年，Hwang等人[19]使用2種方法證明了文獻[18]的方案中，驗證者無法驗證簽名是否合法。2001年，Hwang等人[3]提出了2種簡單批量驗證多個數字簽名的算法：BV-DSA與BV-RSA，其中BV-RSA方案與文獻[18]方案具有相同的安全缺陷，即不誠實的簽名者可以偽造個人數字簽名，使虛假的批量驗證有效。2006年，Bao等人[20]針對文獻[3]中的BV-RSA方案進行了密碼分析與改進。2017年，Kittur等人[21]針對RSA數字簽名算法，提出了一種快速驗證方案，研究了各種RSA數字簽名算法的批量驗證方法，指出數字簽名批量驗證在物聯網應用中是一個很有前途的研究方向。

ECDSA數字簽名驗證算法相比于DSA和RSA算法，具有速度快、強度高和簽名短等優勢[22]。ECDSA*是ECDSA的一種改進，它能應用于Naccache等人[1]針對DSA數字簽名提出的批量驗證算法中。2005年，Adtipa等人[23]提出了一種加速驗證ECDSA數字簽名的方案，能夠加速驗證ECDSA簽名的效率，在不增加算法復雜度的前提下，使其效率提升40%以上。 2007年，Cheon等人[4]設計針對ECDSA*數字簽名設計了一種快速批量驗證多個數字簽名的方案，針對相同簽名者與不同簽名者提出了不同的批量驗證算法。2012年，Bernstein等人[24]針對橢圓曲線簽名提出了一種快速批量偽造識別的策略，進而降低了橢圓曲線簽名批量偽造識別的成本。2014年，Karati等人[25]提出了一種新的ECDSA數字簽名批量驗證算法。2019年，Kittur等人[26]針對ECDSA*提出了一種更高效的批量驗證算法，在不同的批處理規模上表現更好。

3 SM2數字簽名批量驗證算法

定義p為大素數，Fp為有限域.選擇a,b∈Fp作為橢圓曲線E的參數。定義(x,y)為橢圓曲線E上的一點，并且將其作為群G的生成元。群G的階為n。定義Hv()為摘要長度為v比特的哈希算法。

3.1 相同簽名者的批量驗證算法

3.1.1 簽名(Sign)

假設簽名者是A，其公私密鑰對為(dA,PA)，對于待簽名消息Mi，隨機選取ki∈[1,n-1]，計算：

(xi,yi)=kiG

ri=(ei+xi) modn

(1)

si=((1+dA)-1·(ki-ridA)) modn

(2)

簽名者A將(ri,si)(i=1,2,…,l)作為消息Mi的簽名發送給驗證者B。

3.1.2 批量驗證(Batch Verification)

驗證者B收到所有消息的簽名(M′i,r′i,s′i) ((i=1,2,…,l)，步驟1～步驟5中i相同)，進行批量驗證。

步驟1檢驗r′i∈[1，n-1]是否成立，若不成立則驗證不通過。

步驟2檢驗s′i∈[1，n-1]是否成立，若不成立則驗證不通過。

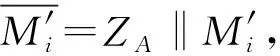
步驟5計算ti=(r′i+s′i) modn，若ti=0，則驗證不通過。

(3)

(4)

(5)

步驟10根據式(4)和式(5)計算橢圓曲線上的點：

(x′,y′)=uG+wPA

(6)

步驟11根據式(3)和式(6)計算R′的值：R′=(d+x′) modn，檢驗R′=R是否成立，若成立則驗證通過；否則驗證不通過。

3.1.3 正確性分析

因為M′=M，(r′,s′)=(r,s)，則e′=e。又因為ri=(ei+xi)(i=1,2,…,l)，則：

對于相同簽名者的批量驗證公式為：

只需驗證：

根據式(1)、式(2)、式(4)、式(5)以及r′i=ri,s′i=si得：

uG+wPA=

kG=(x,y)=右邊

這就證明了批量驗證相同簽名者產生的數字簽名方案的正確性。

3.1.4 安全性分析

定理1在簽名者相同的情況下，SM2數字簽名批量驗證算法是安全的，具有和單個驗證算法一樣的強度。

證明本文利用反證法的思想，證明相同簽名者下SM2批量驗證算法的安全性，即如果SM2批量驗證算法不安全，則可以推導出SM2標準單個驗證算法不安全，故SM2批量驗證算法是安全的。具體證明如下：

在相同簽名者批量驗證方案中，需要驗證:

其中，r′i=s′iG+tiPA+e′i。

假設敵手成功篡改了簽名后的消息Mi，并且能夠滿足：

但不能夠改變簽名后的r1,r2,…,rl。因為簽名過程中針對不同的消息Mi，能夠生成r1,r2,…,rl，敵手必須揭示r1,r2,…,rl是SM2簽名的一部分。

在驗簽過程中，本文計算所有消息Mi的密碼雜湊函數值e′i，根據式(6)計算橢圓曲線上的點(xi,yi)，給定這些xi坐標和驗證條件R=R′，對于相應的y坐標y1,y2,…,yl，r1,r2,…,rl存在唯一的解。只要l被限制為小的常數值，敵手只需要適度的計算就可以確定y1,y2,…,yl的唯一值，這意味著敵手可以揭示坐標xi與ri，進而知道ri的所有點坐標(xi,yi)。

以上論證基于解的唯一性定理，r1,r2,…,rl滿足標準SM2數字簽名驗證條件，若敵手可以篡改SM2數字簽名批量驗證算法中的數據，那么敵手也可以篡改標準SM2數字簽名中算法的數據，因此SM2數字簽名批量驗證算法的安全性不低于SM2單個數字簽名驗證算法的安全性。

□

3.2 不同簽名者的批量驗證算法

假設簽名者是Ai，其公私密鑰對為(dAi,PAi)，針對不同的消息MAi，產生的簽名消息為(rAi,sAi)(i=1,2,…,l)。假設驗證者是B，則B需要對Ai發送過來的簽名(MAi,rAi,sAi)進行驗證，判斷其簽署者是否為Ai。在進行數字簽名驗證過程中，點乘運算是一項非常耗時的運算，即計算橢圓曲線點(x′Ai,y′Ai)=s′AiG+tAiPAi。因此，本文先分別計算出s′Ai與tAiPAi的累加和，再計算橢圓曲線上的點(x′Ai,y′Ai)時，僅需1次點乘運算，進而提高數字簽名驗證效率。

3.2.1 簽名(Sign)

假設簽名者是Ai(i=1,2,…,l)，其公私密鑰對為(dAi,PAi)，對于待簽名消息MAi，隨機選取kAi∈[1,n-1]，計算：

(xAi,yAi)=kAiG，

rAi=(eAi+xAi) modn

(7)

sAi=((1+dAi)-1·(kAi-rAidAi)) modn

(8)

簽名者Ai將(rAi,sAi)作為消息MAi的簽名發送給驗證者B。

3.2.2 批量驗證(Batch Verification)

驗證者B收到所有消息的簽名(MAi,rAi,sAi) ((i=1,2,…,l)，步驟1～步驟5中i相同)，進行批量驗證。

步驟1檢驗r′Ai∈[1,n-1]是否成立，若不成立則驗證不通過。

步驟2檢驗s′Ai∈[1,n-1]是否成立，若不成立則驗證不通過。

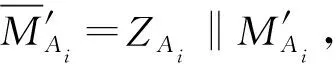
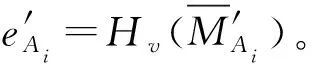
步驟5計算tAi=(r′Ai+s′Ai) modn，若tAi=0，則驗證不通過。

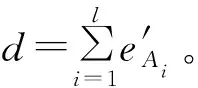
(9)

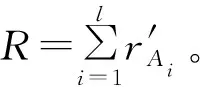
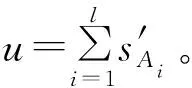
(10)

步驟9根據式(10)計算橢圓曲線上的點：

(11)

步驟10根據式(9)和式(11)計算R′的值：R′=(d+x′Ai) modn，檢驗R′=R是否成立，若成立則驗證通過；否則驗證不通過。

3.2.3 正確性分析

因為M′Ai=MAi，(r′Ai,s′Ai)=(rAi,sAi)，則e′Ai=eAi。又因為rAi=(eAi+xAi)(i=1,2,…,l)，則：

對于不同簽名者Ai的批量驗證公式為：

只需驗證：

根據式(7)、式(8)、式(10)以及r′Ai=rAi,s′Ai=sAi得：

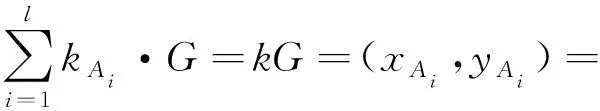
這就證明了批量驗證不同簽名者產生的數字簽名方案的正確性。

3.2.4 安全性分析

定理2在簽名者不同的情況下，SM2數字簽名批量驗證算法是安全的，具有和單個驗證算法一樣的強度。

定理2的證明與定理1的證明相似，略。

4 批量驗證算法的實現與性能分析

為了比較單個驗證算法與批量驗證算法的運行效率，本文使用C語言編程實現2個方案，通過調用OpenSSL密碼庫實現橢圓曲線上的計算。基于PC端開發，運行環境如下：

中央處理器：Intel i5-6300HQ&2.3 GHz；

內存：4 GB；

硬盤：500 GB；

操作系統：Windows 10專業版。

橢圓曲線各參數的取值與GB/T 32918.2-2016中的附錄A.2中各參數的取值一致。

本文分別執行2個方案10次，獲取數據平均值，以ms作為時間單位。在相同簽名者與不同簽名者方案中，密鑰生成階段相同簽名者方案僅需生成1對公私密鑰對，而不同簽名者方案需要生成多對公私密鑰對，因此不同簽名者方案中密鑰生成階段耗時遠大于相同簽名者方案相應階段的耗時；在簽名與驗證過程中，對于相同簽名者與不同簽名者，它們各部分耗時幾乎相同。表1表示在不同消息數量的情況下，相同簽名者與不同簽名者進行單個驗證算法與批量驗證算法的運行時間比較。

從圖1可以看出，單個驗證算法中，點乘運算約占驗證時間的95%以上。在數字簽名驗證過程中，單個驗證算法的時間與消息數量成線性關系，隨著消息數量的不斷增加，驗證時間也相應不斷增長；批量驗證算法中，最耗時的點乘運算與消息數量無關，僅需1次，其他計算雖與消息數量成線性關系，但耗時較少，因此驗證時間不會隨著消息數量的不斷增加而快速增長。圖1中橫坐標2x(x=0,4,8,…,20)表示消息M的數量，縱坐標2y(y=0,4,8,…,24)表示數字簽名驗證所需時間。當簽名數量達到約100萬(220)時，單個驗證算法大約需要1 h，而批量驗證算法僅需2 s。因此，對于大量消息數據同時進行數字簽名的時候，不論是相同簽名者還是不同簽名者，使用批量驗證算法都可以大大縮短運行時間，顯著提高效率。

Table 1 Comparison of run time between single verification algorithm and batch verification algorithm

Figure 1 Comparison of run times between single verification and batch verification algorithm圖1 單個驗證算法與批量驗證算法運行時間比較

5 結束語

本文首次提出了一種高效的SM2數字簽名批量驗證算法，特別適合電子貨幣等需要驗證大量數字簽名的應用場景。批量驗證算法通過減少驗證過程中耗時的點乘運算，顯著縮短整個驗證過程的時間，極大提高了驗證效率。實驗結果表明，當數字簽名數量達到約100萬(220)時，單個驗證算法大約需要1 h，而批量驗證算法僅需2 s。