基于波動理論的聚波器幾何參數設計

段 劍，湯振鶴，孫良文，劉澤軍，王兆旭，王浩全

(1. 山東非金屬材料研究所，山東 濟南 250031； 2. 中北大學 信息與通信工程學院，山西 太原 030051)

0 引 言

在管道內外壓差一定的情況下，氣體會通過管道泄漏孔發出一定頻率的超聲波，依據該聲波信號可以實現泄漏孔的定位和孔徑當量分析[1]. 超聲波具有很強的方向性和衰減性，隨著距離增加，聲壓幅值衰減嚴重. 為了解決這一問題，可以在接收傳感器前增加聚波器的辦法來實現.

本設計利用COMSOL軟件分析了不同形狀、長度及錐度的聚波器內的聲場分布情況，為設計合適的聚波器提供參考.

1 聚波器的數值分析

在波陣面不變的特殊情況下，波動方程可表示為

(1)

聚波器的截面面積是關于x的函數S=S(x).當波陣面形狀隨聚波器截面面積變化時，波動方程解的形式為p=p(x)ejωt，把該解代入式(1) 可得到變系數常微分方程.

(2)

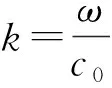
在無反射波的情況下，其解可表示為變系數的指數函數

p(x)=A(x)ejγx.

(3)

從式(3)可得，只要確定了參數A(x)和γ，就可以得出聲壓值[5-7].

將式(3)代入式(2)可得到如下關系式

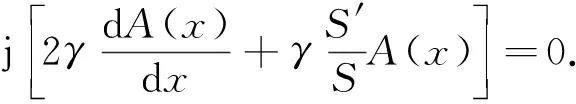
(4)

從式(4)可以看出，當實部與虛部均為0時，等式成立，即

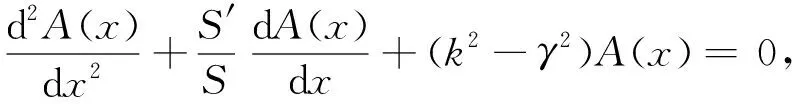
(5)

(6)

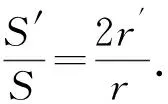
(7)

將式(7)代入式(6)得

(8)

由式(7)、式(8)可知，只需得出聚波器截面半徑與軸向距離的關系，即可得聚波器內部的聲壓幅值[8-10].

2 聚波器截面變化規律及聲場分析

2.1 錐形聚波器

圖 1 為錐形聚波器二維軸對稱圖，長度為l，兩端半徑分別為r1、r0，由圖可知錐形聚波器的截面半徑r與距離x的關系為

(9)

式中：l為聚波器的長度;r0為B端口半徑；r1為A端口半徑.

圖 1 錐形聚波器結構示意圖Fig.1 Schematic diagram of conical wave collector structure

(10)

結合式(10)和式(3)分析可知，隨著聚波器半徑逐漸減小，A(x)逐漸增大，聲壓幅值也逐漸增加. 所以，在超聲波測漏儀中引入錐形聚波器具有增強聲壓幅值的作用.

2.2 指數形聚波器

圖 2 為指數形聚波器的二維軸對稱圖，長度為l，兩端半徑分別為r1、r0，由圖可知截面半徑與距離x的關系為

r(x)=r1eδx，

(11)

式中：r0為聚波器底端的半徑；δ為聚波器的蜿蜒度.

圖 2 指數形聚波器結構示意圖Fig.2 Schematic diagram of exponential wave collector structure

將式(11)代入式(8)和式(9)可得

(12)

(13)

結合式(3)有

(14)

由于指數形聚波器為漸縮形管，所以蜿蜒度δ為負，由式(12)可知，隨距離x的增加，截面半徑逐漸減小，所以A(x)逐漸增大，聲壓振幅逐漸增強.由此可知，指數形管聚波器可以增強聲壓的幅值.

3 仿真模型建立

聚波器為三維軸對稱結構，為了降低計算難度，可使用二維軸對稱結構進行建模. 設聚波器兩端端口分別為A端口和B端口(見圖 3)，其中，B端口半徑為0.8 cm.

圖 3 聚波器二維軸對稱模型Fig.3 Two-dimensional axisymmetric model of wave concentrator

本設計采用壓力聲學物理場下的瞬態接口模型，在A端口上部10 cm處設置一個頻率為40 kHz 的聲源，聲源振動的法向速度如圖 4 所示.

圖 4 聲源振動的法向速度Fig.4 Normal velocity of sound source vibration

本文僅對聚波器的幾何參數進行分析，不考慮材料屬性，因此，設置聚波器的邊界為硬聲場邊界. 為防止其余邊界對檢測結果造成影響，在剩余邊界處添加完美匹配層和阻抗邊界以防止聲波反射的干擾.

4 實驗結果與分析

在COMSOL軟件中分別建立錐形聚波器模型和指數形聚波器模型，設置聚波器長度均為10 cm，A端口截面半徑均為2.56 cm，經網格劃分及仿真計算可得聲壓分布圖，如圖 5，圖 6 所示.

圖 5 錐形聚波器聲壓分布圖

圖 6 指數形聚波器聲壓分布圖Fig.6 Sound pressure distribution diagram of exponential wave collector

聲波進入聚波器后，經聚波器壁面的反射不斷疊加，使其聲壓不斷加強，與上述理論推導結果相符. 通過比較圖 5 和圖 6 兩種聚波器可知，在A端口截面面積相同的情況下，聲波在錐形聚波器中疊加效果明顯優于指數形聚波器.

為了更直觀地比較錐形聚波器與指數形聚波器的效果，分別在聚波器的中心軸上設置5個測量點，距離間隔2 cm. 測量結果如圖 7 所示.

圖 7 聚波器軸向距離的聲壓Fig.7 Sound pressure of axial distance of wave concentrator

通過比較圖 7 中的折線，可以直觀地看出指數形聚波器聲壓在8 cm處達到最高，大約為1 Pa，而錐形聚波器的聲壓為逐漸遞增.

4.1 錐形聚波器對聲壓的影響

當錐形聚波器的錐度10°時，對長度范圍7 cm～15 cm的錐形聚波器進行仿真分析，得到錐形聚波器長度與聲壓的關系圖，如圖 8 所示.

圖 8 錐形聚波器長度與聲壓的關系Fig.8 Relationship between the length of conical wave collector and sound pressure

聚波器對聲壓的增強與聲波在聚波器內的疊加有關，在一定范圍內，聲波疊加次數越多，其聲壓越強. 由圖 8 可知，聚波器長度為11 cm時，對聲壓的增強效果最好.

當錐形聚波器長度為11 cm時，對錐度范圍為7°～15°的錐形聚波器進行仿真分析，可得到錐度與聲壓的關系圖，如圖 9 所示.

圖 9 錐形聚波器錐度與聲壓的關系Fig.9 Relationship between taper and sound pressure of conical wave collector

從圖 9 可以看出，錐形聚波器的錐度為10°時，B端口的聲壓值最高，約為1.33 Pa.

4.2 指數形聚波器對聲壓的影響

對于指數形聚波器，在蜿蜒度為-9的情況下，對長度范圍7 cm～15 cm的情況作了仿真分析，得到長度與聲壓的關系圖如圖 10 所示，由圖可知，指數形聚波器長度為14 cm時效果最好.

圖 10 指數形聚波器長度與聲壓的關系Fig.10 Relationship between length of exponential wave collector and sound pressure

當指數形聚波器長度為14 cm時，指數隨聲壓的關系圖如圖 11 所示.

由圖10、圖11可知，指數形聚波器長度為14 cm，蜿蜒度為-8時效果較好，但與錐形聚波器相比，效果較差.

圖 11 指數形聚波器蜿蜒度與聲壓的關系Fig.11 Relationship between sinuosity and sound pressure of exponential wave concentrator

5 結 論

本文從質點振動出發，在建立超聲波在介質中傳播波動方程的基礎上，假設無反射波的情況下，推導出了聚波器內部的聲壓與截面半徑和軸向距離的數學表達式. 利用COMSOL軟件進行了仿真實驗，得出長度為12 cm錐度為10°的錐形聚波器對聲壓幅值影響最大的結果，為工程應用奠定了基礎.