縮小參數范圍 優化解題過程

黃治元

(浙江省寧波市鄞州中學 315104)

含參數的最值問題、恒成立問題是高考數學中的熱點問題，解題方法一般是通過對參數進行分類討論，但分類情況比較多時就會顯得繁瑣復雜.若先縮小參數范圍再加以討論，則往往會優化解題過程.

一、利用特值檢驗，縮小參數范圍

對于某個一般性的數學問題，如果一時難以解決，那么可以先解決它的特殊情況，即從研究對象的全體轉變為研究屬于這個全體中的一個對象或部分對象.

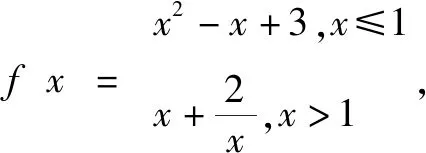
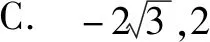
解析這是2017年天津市高考理科試題選擇題第8題，標準解答如下：

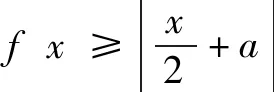
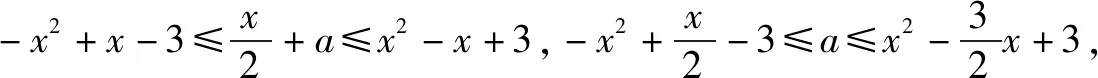
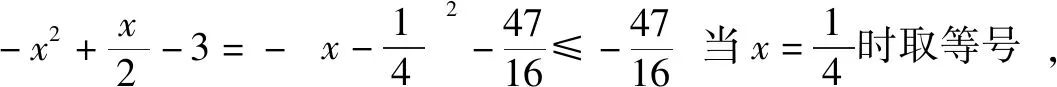
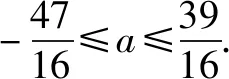
當x>1時，(*)式為

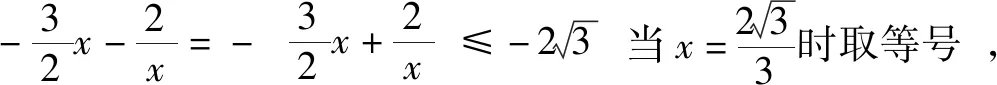
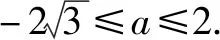
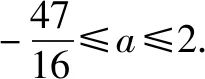
故選A.

評注此法思路過程雖嚴謹清晰，但有點“小題大做”，不符合選擇題的解題特點.快速找出正確答案才是上策，解法如下：

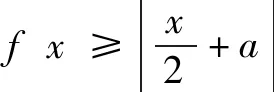
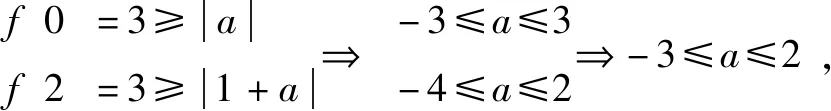
例2 已知a>0，函數f(x)=|x2+|x-a|-3|在區間[-1,1]上的最大值是2，則a=____.

解析函數f(x)帶有雙重絕對值，絕對值函數問題一般是先去掉絕對值符號轉化為分段函數，但本題去掉內層絕對值轉化為分段函數后不易確定相應的自變量x的范圍，這給后續分類討論帶來不便.若先縮小參數a的范圍，問題得到解決.

解法如下：f(0)=||a|-3|=|a-3|≤2(a>0)?1≤a≤5，

∴當x∈[-1,1]時，f(x)=|x2-x+a-3|.

∴f(-1)=|a-1|≤2?-1≤a≤3，從而1≤a≤3.

∴f(x)=|x2-x+a-3|，x∈[-1,1],1≤a≤3

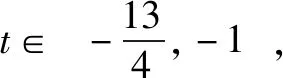
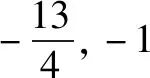
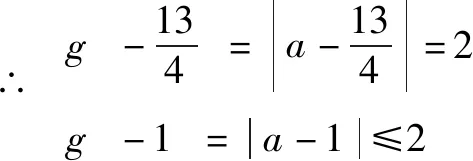
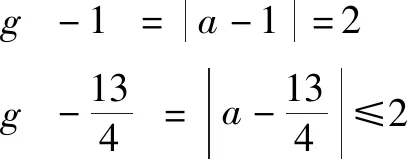
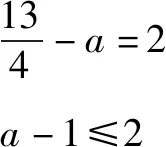
評注在得知1≤a≤3的情況下，求解①，②也更快捷.

例3設函數f(x)=3|ax|-(x+a)2，其中a∈R.若對任意x∈[a,a+1]，恒有f(x)≥-1，求實數a的取值范圍.

解析先縮小參數a的取值范圍找其使命題成立的必要條件，有時該必要條件也恰好是使命題成立的充分條件，接下來證明其充分性即可.

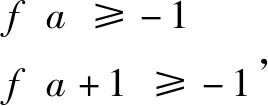
下面證明，當a∈[-1,0]時，對任意x∈[a,a+1]，恒有f(x)≥-1.

(1)當a≤x≤0時，f(x)=-x2+ax-a2，f(a)=f(0)=-a2≥-1，故f(x)≥min{f(a),f(0)}≥-1成立；

(2)當0≤x≤a+1時，f(x)=-x2-5ax-a2，f(a+1)≥-1，f(0)≥-1，

故f(x)≥min{f(a+1),f(0)}≥-1成立；

由此，對任意x∈[a,a+1]，恒有f(x)≥-1.

所以實數a的取值范圍是[-1,0].

例4已知函數f(x)=x2-ax，|f(f(x))|≤2在[1,2]上恒成立，則實數a的最大值為____.

解析利用從一般到特殊的解題思想，特值檢驗縮小參數a的范圍，猜測實數a的最大值，先猜后證.

由f(f(x))=f(x2-ax)=(x2-ax)(x2-ax-a)知|f(f(x))|≤2,即|(x2-ax)(x2-ax-a)|≤2對x∈[1,2]上恒成立，特別地，當x=1,2時，有

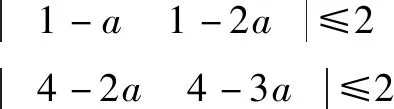
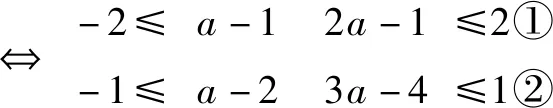
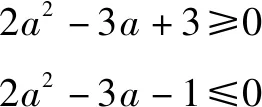
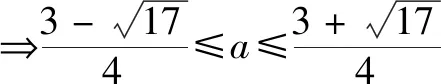
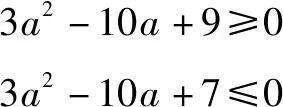
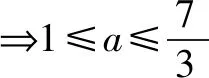
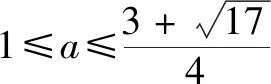
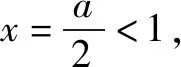
∴當x∈[1,2]時，f(1)≤f(x)≤f(2)，

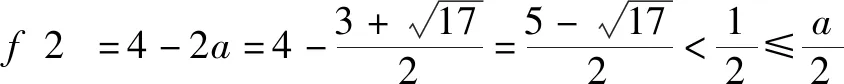
所以f(x)=x2-ax在[f(1),f(2)]上遞減，

由f(1)≤f(x)≤f(2)

得f(f(2))≤f(f(x))≤f(f(1))

所以-2≤f(f(x))≤2，

即|f(f(x))|≤2.

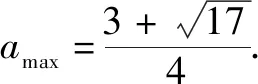
二、利用極限思想，縮小參數范圍

極限思想是一種重要的數學思想，靈活地借助極限思想解題，往往可以避免復雜的討論，優化解題過程.

例5設a∈R，若x>0時，均有[(a-1)x-1](x2-ax-1)≥0，則a=____.

解析此題是2012年浙江理科卷最后一個填空題.經初步分析知，需要對不等式中的兩個因式的正負進行討論，也需對因式(a-1)x-1中一次項系數a-1的正負進行討論.討論情況有些復雜，先考慮縮小參數a的取值范圍.

注意到，當x→+∞時，x2-ax-1→+∞，

∴a-1>0?a>1

[(a-1)x-1](x2-ax-1)≥0對x>0恒成立，

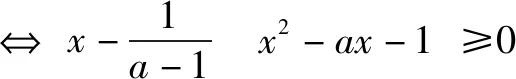
例6若不等式(ax+3)(x2-b)≤0對任意的x∈(0,+∞)恒成立，則( ).

A.ab2=9 B.a2b=9，a<0

C.b=9a2，a<0 D.b2=9a

解析含有兩個參數的不等式恒成立問題，分類討論情形復雜，優先考慮縮小參數范圍.

注意到，當x→0+時，ax+3>0，從而x2-b≤0?b>0.

當x→+∞時，x2-b>0，從而ax+3≤0，?a<0.

∴(ax+3)(x2-b)≤0對任意的x∈(0,+∞)恒成立，

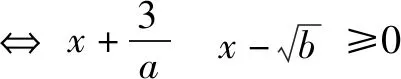
含參數的最值問題、恒成立問題，優先考慮縮小參數的范圍以達到簡化分類討論或是避免分類討論的目的.至于選擇怎樣的特殊值來檢驗縮小參數范圍，這需要一個嘗試的過程，一般會選擇區間的端點值(或取其極限)，或是選擇給定區間內的某個便于計算的值，這因題而異.