基于修正反應譜法的簡支橋梁減隔震性能研究

張西丁

(廣東省交通規劃設計研究院股份有限公司,廣東 廣州 510507)

0 引 言

我國是地震多發國家，近年來地震發生頻繁，造成大量結構毀壞。橋梁作為生命線工程，一旦失效將導致重大生命和經濟損失。因此對橋梁進行抗震性能分析與評價是極其重要的。我國已建和在建的橋梁中，橋型以中小跨徑的鋼筋混凝土或預應力混凝土梁橋為主，下部結構通常采用樁柱式輕型橋墩[1]。對于這類橋梁，通常采用延性設計和減隔震設計兩種抗震體系。延性設計通過利用橋梁墩柱發生塑性變形，延長結構周期，耗散地震能量，缺點是震后橋墩發生了塑性變形不易修復；減隔震設計利用橋梁上、下部結構的連接構件(支座、耗能裝置)發生塑性變形或增大阻尼，延長結構周期，耗散地震能量，從而減小結構地震反應，橋墩保持在彈性范圍，震后通過更換減隔震支座即可恢復正常使用[2,3]。因此，現在減隔震體系被越來越多地應用到抗震設計中。減隔震橋梁抗震分析可采用反應譜法、時程法和功率譜法。反應譜法是線彈性分析方法，方法簡潔，在一定條件下，對減隔震橋梁進行等效線性化處理，可采用反應譜法進行減隔震橋梁的抗震分析。研究表明，只考慮結構的水平地震作用時，多振型反應譜法通過迭代計算可以得到較理想的計算結果[4,5]。

唐光武等[6]以3×40 m連續T梁橋為依托，基于單自由度模型的單振型反應譜法修正方法，得出了考慮減隔震裝置特性單自由度橋梁的等效結構阻尼比，以此來修正設計反應譜，求得地震地震響應。程玉營[7]基于4×25 m連續小箱梁橋，研究了單模態和多模態反應譜迭代法對減隔震分析的適用性，和時程結果對比，可用度較高。目前關于反應譜迭代法在簡支梁橋中的適用性研究的文獻很少。

本文以橋梁設計中常用的30 m簡支梁橋為背景，利用有限元軟件MIDAS Civil，基于新版抗規中的多振型反應譜迭代法進行分析，并與時程分析結果進行對比，探討該方法對減隔震設計的適用性。此外，通過對支座等效剛度和全橋等效阻尼比等迭代參數進行研究，探索出一種簡化的迭代方法。

1 工程概況及有限元建模

1.1 項目介紹

某路基寬度為26 m雙四高速公路，橋梁采用2×12.75 m分幅布置，單幅橋面凈寬12.5 m。橋梁上部結構采用多聯3×30 m先簡支后橋面連續預制小箱梁結構，梁高1.6 m。下部結構采用D140-D160 cm樁柱式橋墩。橋梁斷面形式如圖1所示。該高速公路橋址區場地土為軟弱土～堅硬土，場地類別為Ⅲ類，抗震設防烈度為Ⅶ度，基本地震加速度值為0.10g，反應譜特征周期為0.45 s。橋梁采用減隔震體系，支座選用高阻尼橡膠支座，型號為HDR(Ⅰ)-520×181-G0.8-e80，每片小箱梁兩端各布置一個支座。

圖1 橋梁橫斷面圖(半幅)

1.2 有限元模型建立

1.2.1 支座的模擬

根據文獻[2]，高阻尼支座的恢復力模型可采用雙線性模擬，其恢復力模型如圖2所示。由文獻[3]可查出支座的設計參數，屈服前水平剛度Ku=946 kN/mm;屈服后水平剛度Kd=949 kN/mm;屈服強度Fy=81 kN;水平等效剛度Keff=1.95 kN/mm;支座等效阻尼比ζ=015。應用時程法計算時，用雙線性彈塑性單元來模擬高阻尼支座，這種模型可以考慮高阻尼橡膠支座的非線性耗能特性。

圖2 高阻尼支座的恢復力模型

1.2.2 有限元模型

采用MIDAS Civil 2020建立單梁模型模擬上部結構；時程法計算時，采用等效雙線性模型模擬高阻尼橡膠支座；修正反應譜法計算時，采用彈簧來模擬支座；采用一般彈性支承(6個方向的剛度)模擬樁土相互作用。樁基彈性剛度模擬時應考慮樁土相互作用，按照m法計算樁土水平剛度，m取值按照《公路橋涵地基與基礎設計規范》(JTG 3363-2019)中規定，并考慮2.5倍動力放大系數。考慮到相鄰結構對邊界條件的影響，建立三聯橋梁結構，選取中間一聯結果作為研究對象；反應譜的設計參數按新版抗規[2]選取。取橋墩高度等高H=10 m，橋梁有限元模型如圖3所示。

圖3 橋梁有限元模型

2 修正反應譜法分析

根據新版抗規[2],采用多振型反應譜法進行抗震分析時，應采用迭代方法分別計算順橋向和橫橋向的地震響應，迭代過程為：

(1)建立模型，各支座剛度可取屈服前初始剛度，全橋等效阻尼比取0.05。

(2)進行多振型反應譜計算，根據求得的支座位移利用雙線性模型求得支座等效剛度，和橋墩剛度串聯求得結構等效剛度，進而得出全橋等效阻尼比。

(3)根據求得的支座等效剛度修正計算模型，并按全橋等效阻尼比修正 0.8 倍一階振型周期及以上周期的反應譜值，得到修正的設計加速度反應譜。

(4)重新進行抗震計算，得出支座位移，迭代，直到兩次支座位移相差不大于3%，迭代結束。

下面將利用此方法對結構進行順橋向的地震作用分析，并與時程計算結果進行對比，以此驗證此方法在簡支梁橋減隔震分析時的合理性。

2.1 初始迭代剛度的選擇

根據新版抗規[2],取支座屈服前的水平剛度Ku=949 kN/mm作為初始迭代剛度，進行抗震計算。由于上部結構為簡支結構，可選取一跨中的一個橋墩結果進行分析，考慮到邊界條件的影響，選取中間聯中間跨的橋墩為研究對象。經計算，反應譜作用下中間墩的支座位移為18.2 mm，根據規范方法計算出的全橋等效阻尼比ζ=0.0158，遠小于混凝土結構的阻尼比0.05，這是不合理的，原因如下：

(1)一般來說，混凝土結構的阻尼比為0.05。減隔震橋梁設計的隔震原理就是通過增大結構阻尼、延長結構自振周期來消耗地震能量和降低結構地震響應，所以使用了減隔震支座后的全橋阻尼比應大于0.05。

(2)支座位移為18.2 mm，已經大于其屈服位移8.54 mm，說明支座已經發生了屈服，屈服后支座的水平剛度下降得很快，大約為初始剛度的1/6。此時支座的等效剛度與初始水平剛度相差較大。

(3)若繼續按照此方法迭代，用得出的等效阻尼比0.0158去修正反應譜曲線，譜值會變大，這與預期的譜值減小相反。

綜上，應該更改初始迭代剛度的取值。考慮到此時支座已經屈服，雖然不能明確地得出支座位移，但是可以利用支座在設計位移下的等效剛度Keff=1.95 kN/mm作為初始迭代剛度來進行迭代。取設計位移下支座的水平等效剛度 作為初始迭代剛度，帶入模型重新計算。經計算，支座位移為77.6 mm，全橋等效阻尼比ζ=0.0868>0.05，結果是合理的。繼續迭代，最終經過3次迭代后，支座位移與上一次結果的誤差為0.8%<3%，滿足要求，迭代終止。具體的迭代過程見表1。

表1 多振型反應譜迭代結果(墩高10 m)

從以上分析可以看出，使用支座在設計位移下的水平等效剛度作為初始迭代剛度進行分析是有效的。為了驗證此方法的適用性，下面與時程計算結果進行對比。

2.2 非線性時程分析

在結構地震反應時程分析中，如何選擇輸入的地震波，是一個很重要的問題。當選擇地震波時，應該考慮地震動三要素，即地震動強度、地震動譜特性、地震動持續時間[8]。根據該橋梁地震烈度和場地土類別，通過3條模擬人工波作為本次時程分析的地震動輸入，時程分析結果取E2地震作用下的 3 條地震波對應結果的最大值。地震波如圖3所示，將地震波輸入到MIDAS Civil模型中，進行非線性時程分析。

為了比較修正反應譜法(以下簡稱方法一)和時程分析法(以下簡稱方法二)的結果，選取支座位移、支座等效剛度和墩底彎矩作為研究對象，結果對比見表2。從表2中可以看出，方法一的支座位移比方法二大14.5%，而支座等效剛度小約7%，兩者不是成比例的，體現了支座的非線性特性，從支座等效剛度來看，兩者之間差別很小。作為結構的地震響應指標(墩頂位移和墩底彎矩)，方法一比方法二的結果大了約18%，這是因為即使支座等效剛度相差不大，但修正反應譜法地震輸入用的是修正以后的反應譜特性，通過彈性分析得到的結果；而方法二是考慮了支座的非線性特性和支座耗能得到的結果。綜上可以認為修正反應譜法結果是合理的，并且方法一的地震響應比方法二偏高，這在設計中是偏安全的。

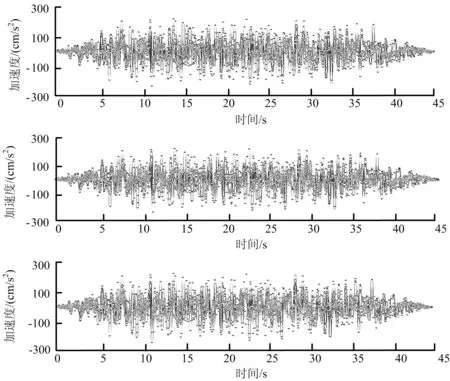
圖4 E2地震波時程曲線

表2 方法一和方法二結果對比表(墩高10 m)

2.3 墩柱高度的影響

2.3.1 減隔震橋梁的合理范圍

減隔震設計是通過增大阻尼，延長結構周期來耗散地震能量，從而減小結構地震反應。當墩高增大時，結構剛度減小，周期變大，通過延長周期效果變得不明顯。因此，首先需要確定簡支梁橋減隔震設計的合理應用范圍，然后在這個范圍內研究修正反應譜法的適用性。

陳光等[4]研究了不同墩高下減隔震支座對橋梁地震反應的影響，發現隨著墩高的增加，減隔震體系體系周期增加，延長周期和減隔震效果不明顯，建議在墩高較高時謹慎對待。魏思斯[5]通過對40 m連續T梁橋在不同墩高下橋墩地震工況的內力、位移響應進行研究，當墩高不超過20 m且采用圓形雙柱墩時，鉛芯隔震橡膠支座能大幅降低橋墩的地震響應；當墩高大于20 m但不超過40 m且采用矩形雙柱墩時，鉛芯隔震橡膠支座能一定程度地降低橋墩的地震響應，減隔震效果隨著墩高增加而降低，建議減隔震支座適用于橋墩墩高不超過40 m的連續梁橋。目前對于簡支梁橋減隔震設計的合理應用范圍研究得還不多。

為了研究橋墩墩高對高阻尼橡膠支座減隔震效果的影響，結合既有文獻[5]的研究成果，本文選取墩高分別為5、10、15、20、25 m的5個工況的進行非線性時程分析。僅研究等高橋梁的結果，不考慮同一聯中墩高差異對結果的影響。各工況墩高具體取值以及對應的橋墩結構形式見表3。

表3 等高簡支梁各工況結構布置

為了保證結果的真實性，采用時程分析模型，通過比較高阻尼橡膠支座和板式橡膠支座兩種方式下的地震效應，來分析減隔震支座的減震效果，從而總結其合理適用范圍。高阻尼支座的設計參數如前文所示，板式橡膠支座參數見表4。

表4 板式橡膠支座參數表

定義減震率Δ為:

(1)

式中：S1為減震前結構的效應值(采用板式橡膠支座)；S2為減震后結構的效應值(采用高阻尼橡膠支座)。

經計算，減震前后結構的地震效應見表5。從表5中可以看出，減震率與墩高密切相關。墩高越大，減震率越低，減震率由38%下降到8%，墩高25m時，減震效果基本很小，采用減隔震設計已經不合理。作者認為采用減隔震支座后，結構的地震響應至少能減小20%才是一個合理的范圍。因此，對于此類橋梁，建議在墩高小于15 m的情況下采用減隔震支座。

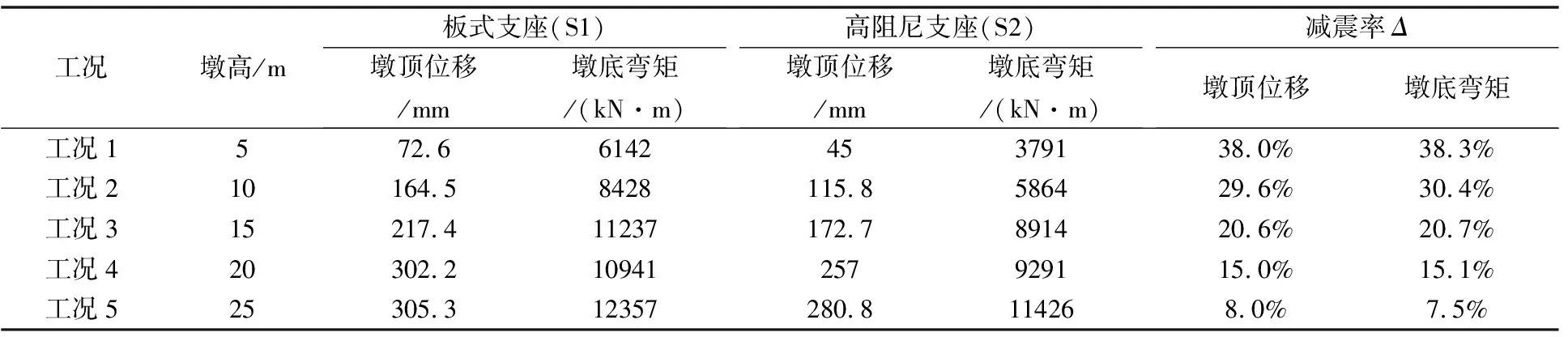
表5 減震前后效應對比表

2.3.2 修正反應譜法迭代

結合減隔震簡支橋梁的合理應用范圍，選取墩高小于15 m的多種工況，建立修正反應譜模型(方法一)，使用支座的等效剛度作為初始迭代剛度，用全橋等效阻尼比來修正0.8倍一階振型周期及以上周期的反應譜值，通過迭代獲得結構的地震響應，并和對應的時程法(方法二)結果進行比較，以此驗證修正反應譜法在不同墩高的適用性。橋墩的地震響應選取墩頂位移和墩底彎矩2個指標。各工況墩高具體取值以及對應的橋墩結構形式見表6。

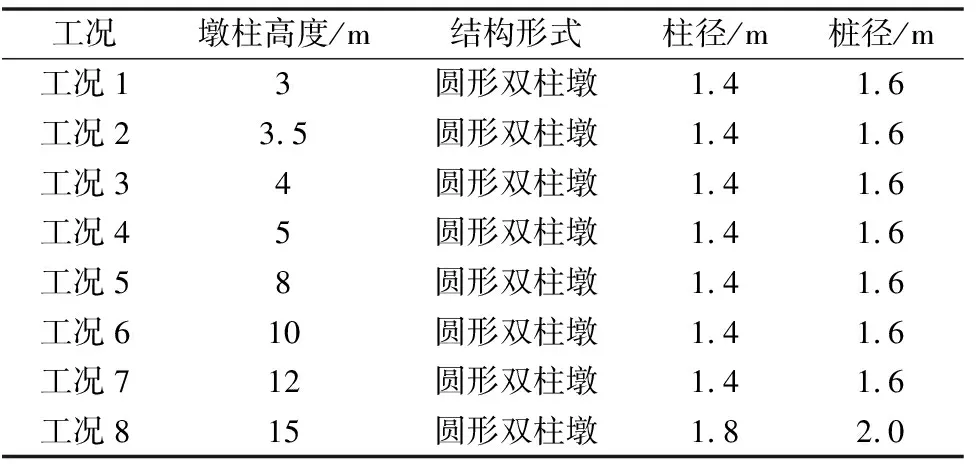
表6 等高簡支梁各工況墩高布置

經過計算，不同工況下的模型經過3～4次迭代，支座位移均能收斂，方法一和方法二的結果如圖5所示。

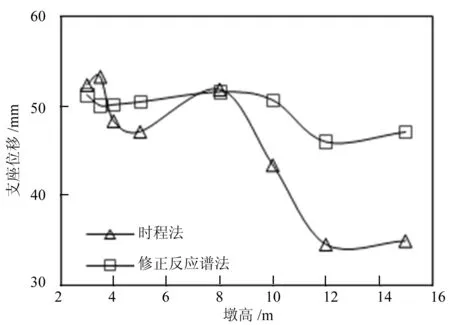
從圖5中可以看出，墩高小于8 m時，兩種方法的計算結果相差不大；墩高大于8 m后，兩種方法的計算結果開始拉開，但差值基本維持在一個穩定的范圍。

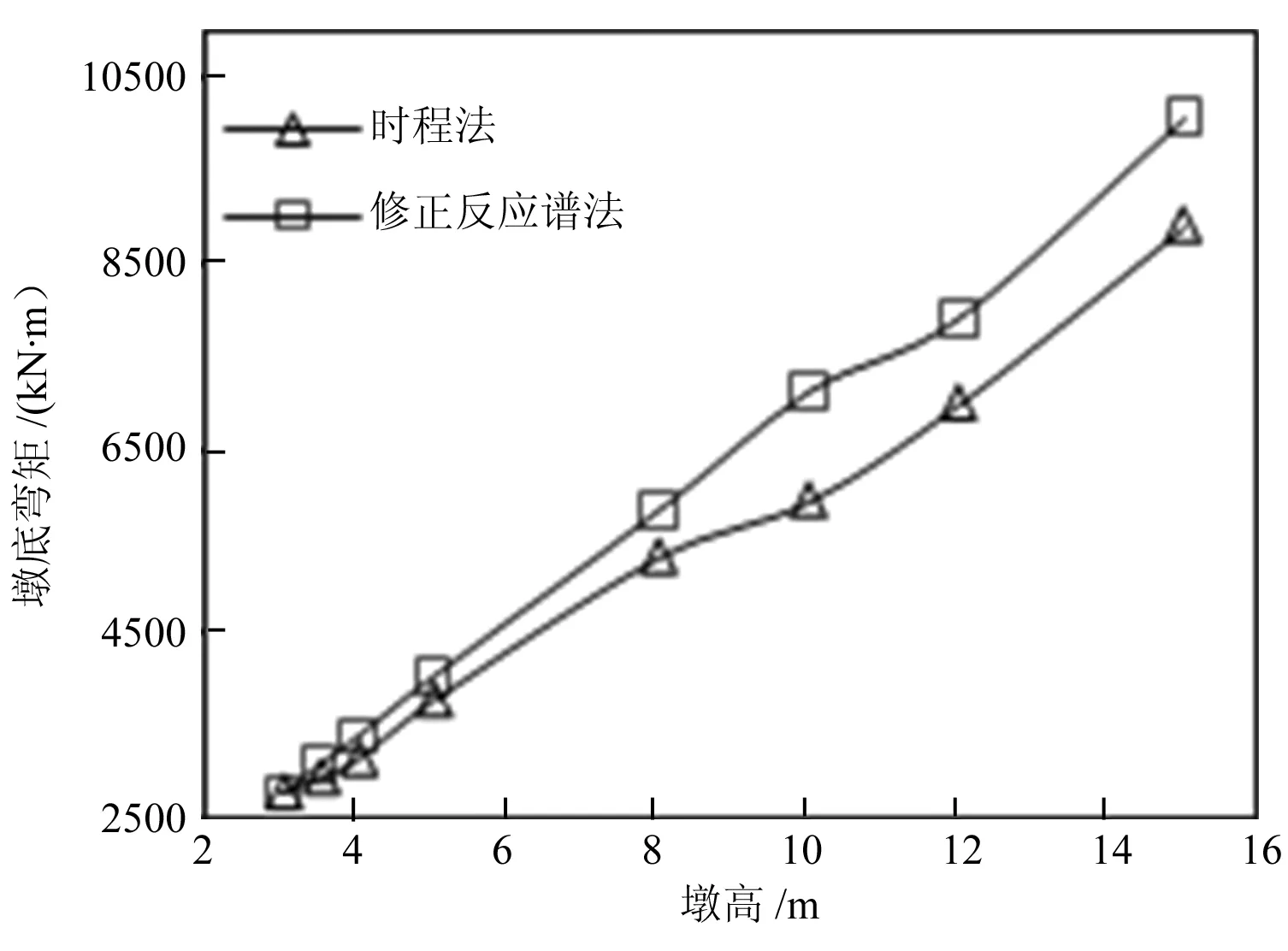
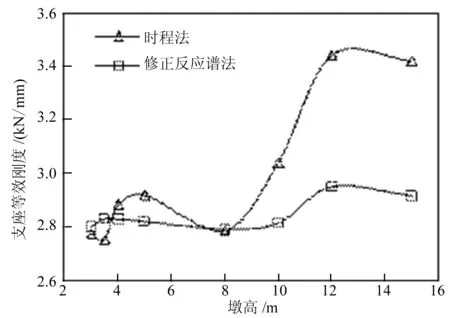
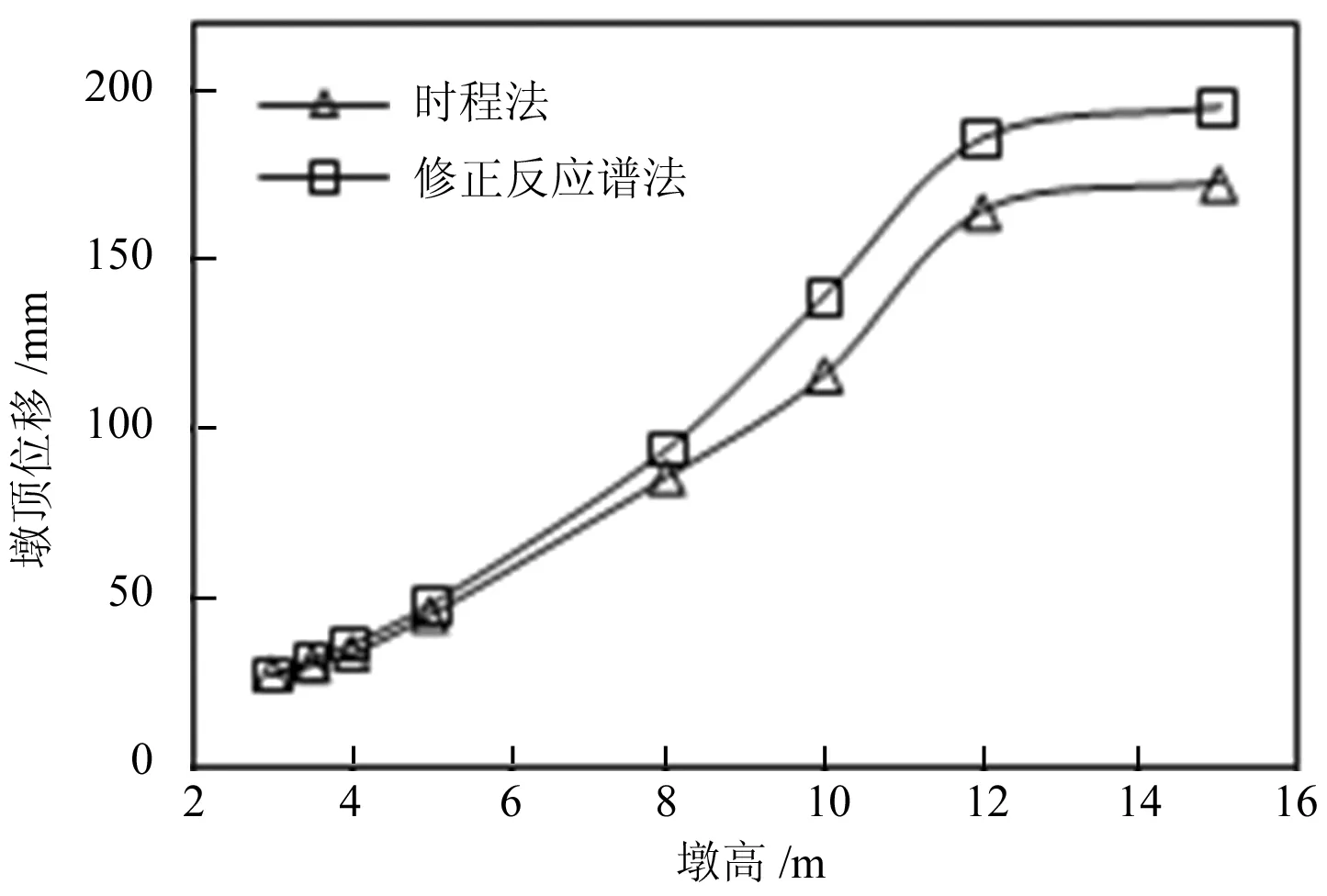
圖5 不同墩高下的支座特性和地震響應

(1)支座位移和等效剛度。墩高小于8 m時，兩種方法得出的支座位移相差在7%以內，由支座位移反推的支座等效剛度相差3%以內；墩高大于8 m時，支座位移相差在15%～35%，支座等效剛度相差在7%～15%，墩高越大，誤差越大。支座位移的誤差大約是支座剛度誤差的2倍，這是因為由于支座的非線性特性，超過屈服位移后，支座剛度會減小，故支座剛度的誤差小于位移的誤差。

(2)墩頂位移和墩底彎矩。修正反應譜的結果大于時程法結果，但兩種方法得出的墩頂位移和墩底彎矩的差值百分比基本相等。墩高小于8m時，誤差在10%以內；墩高大于8m時，誤差在10%～15%。誤差與墩高沒有明顯的相關性。從地震響應來看，修正反應譜的結果對于設計偏安全，且誤差也在可以接受的范圍內。

綜上，可以認為采用支座的等效剛度作為初始迭代剛度，用修正反應譜法來計算減隔震橋梁是合理的，結果的可信度較高。

3 修正反應譜的簡化方法

修正反應譜法計算需要經過多次迭代，每次迭代后都要根據新的支座剛度和修正的反應譜值來修正模型，這樣計算起來就比較麻煩。若找到一種簡便的方法來減少迭代次數，在保證結果可靠性的前提下簡化計算過程，修正反應譜法的適用性將大大提高。從方法原理和迭代過程可以看出，最終迭代的支座等效剛度和全橋等效阻尼比是兩個關鍵的參數。下面將對這兩個關鍵參數進行分析。

不同墩高下的支座點下剛度和全橋等效阻尼比見表7，其中修正反應譜法下的支座等效剛度為最終迭代的結果，時程法下的支座剛度是由位移反推的結果。

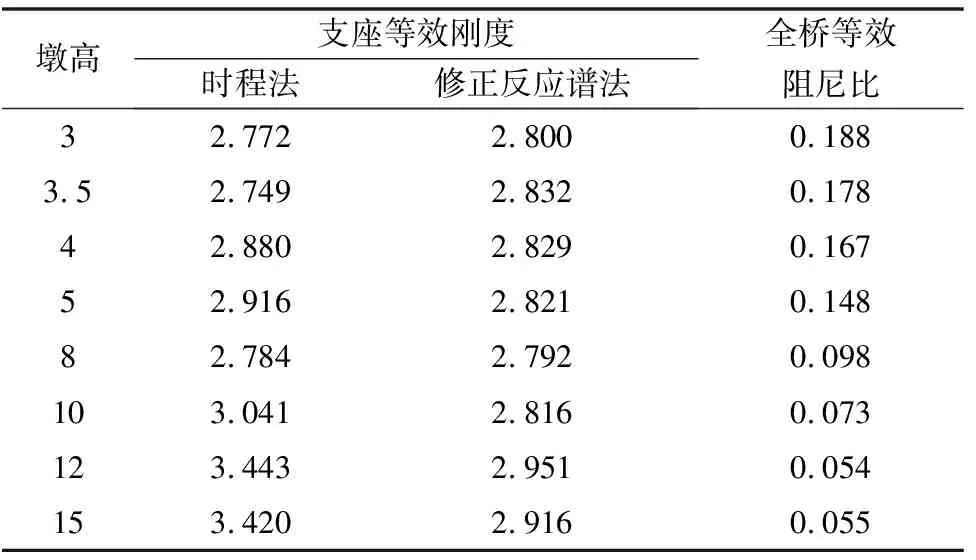
表7 不同墩高下的支座剛度和結構阻尼比

從表7中可以看出，隨著墩高的增大，支座等效剛度在增大，全橋等效阻尼比在減小。

(1)支座等效剛度變化不大。時程法在2.8～3.4 kN/mm變化幅度為20%；修正反應譜法在2.8～2.9 kN·mm變化幅度為5%。

(2)全橋等效阻尼比在0.055～0.188之間，變化幅度71%。兩者的大小都與下部結構剛度有關系。

鑒于支座剛度的變化較小，可以假定不同墩高下的剛度為定值，下面重點分析全橋等效阻尼比的變化規律。

3.1 全橋等效阻尼比

對于減隔震橋梁的全橋等效阻尼比，蘭海燕[9]總結了目前隔震橋組合阻尼比的確定方法，人們早期的研究不多，如美國AASHTO(1991)確定隔震橋梁阻尼比時不考慮橋墩的剛度和阻尼，直接等于隔震支座的等效阻尼比；Turkington 等(1989)則將隔震裝置阻尼比與結構阻尼比直接相加作為系統的阻尼比。隨著研究和認識的進一步深入，現在多采用模態(振型)應變能理論方法給出計算公式，如日本的抗震規范[10]給出了考慮隔震支座、墩、基礎平動、基礎轉動的阻尼比、剛度、支座位移的計算公式，但是計算復雜；Hwang[11]通過將規則橋梁簡化為雙自由度模型，采用經典阻尼理論，給出的2自由度情況下的振型阻尼比計算公式；黃建文[12]基于雙自由度模型，進一步簡化為以隔震模態為主的為單自由度體系，并對設計參數進行了研究。

以上研究都得出，隔震結構的等效阻尼比與減隔震支座和橋墩剛度有關系，但是以上方法的計算公式復雜，涉及到多個參數，不利于簡化計算應用。定義剛度比為式(2)，墩柱剛度為排架墩剛度，支座剛度為一個墩位處支座等效剛度之和，支座等效剛度由支座位移反算得到。

(2)

(3)

式中：Kp為墩柱剛度；Keff為單個支座等效剛度;d,Qdi,Kd,i分別為減隔震支座位移、特征強度、屈服后剛度。

下面研究全橋等效阻尼比和剛度比的關系，假設支座的剛度為定值，Keff=2.9 km/mm,求得橋墩剛度來計算剛度比。以全橋阻尼比ξeq作為因變量，剛度比μ為自變量，將不同墩高下的數據作圖，如圖6所示。添加趨勢線，可以得出公式(4)，回歸分析的相關系數趨近1，可信度很高，全橋阻尼比和剛度比有關。

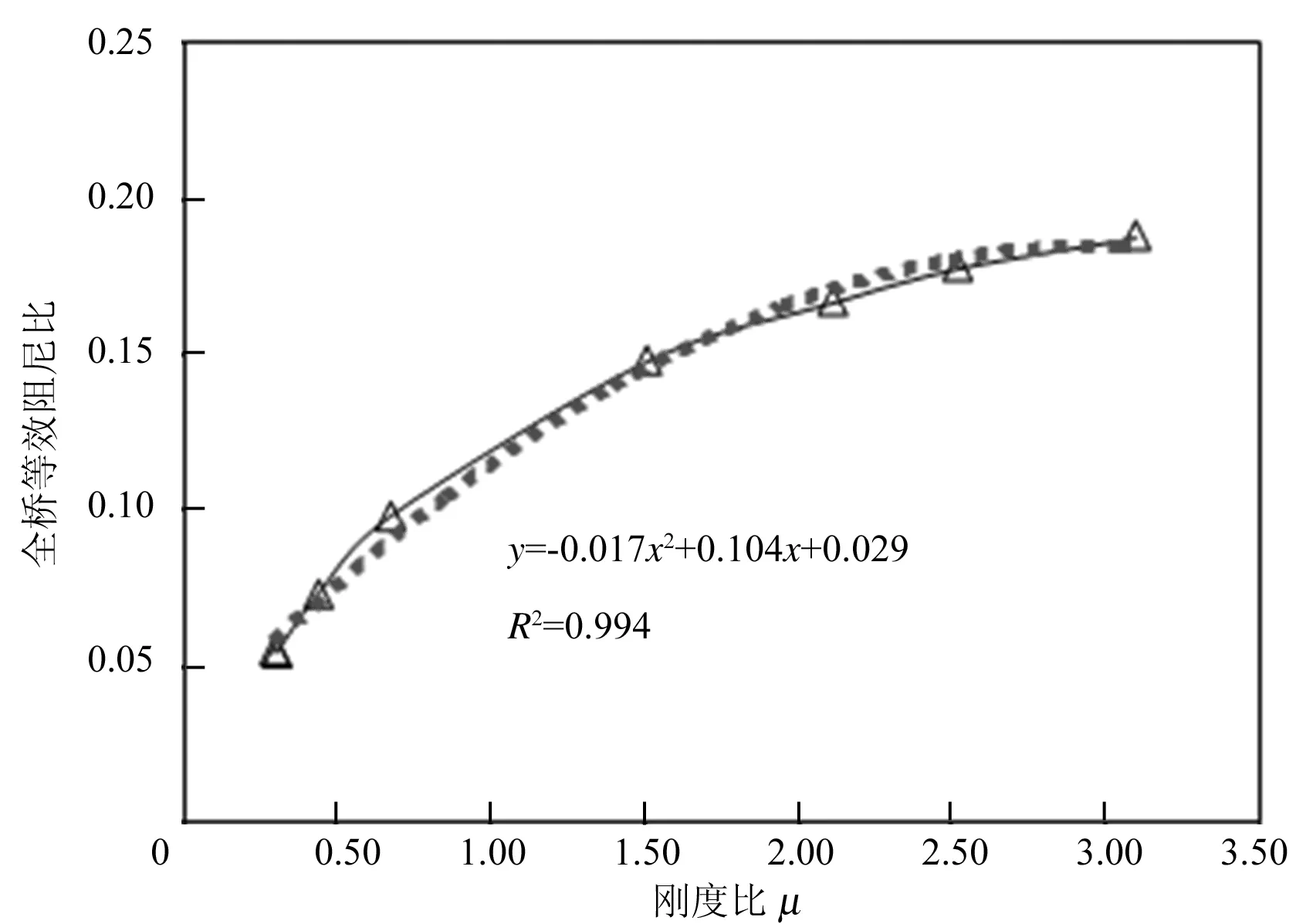
圖6 不同墩高下的全橋等效阻尼比

ξeq=-0.017μ2+0.104μ+0.29

(4)

3.2 迭代過程

根據假定的支座剛度和由公式(4)求得的全橋等效阻尼比，已經很接近最終迭代的結果，這樣修正反應譜法的迭代過程大大簡化。根據前文分析，修正反應譜法和時程法相比，支座剛度的誤差約是支座位移的一半，而新版抗規的收斂條件為支座位移與上一次結果相差3%，因此，簡化修正法的收斂條件可定為：支座等效剛度與上一次結果相差1.5%。具體迭代過程如下：

(1)假設支座的剛度為定值，即Keff=2.9 kN/mm，作為初始迭代剛度。

(2)計算橋墩剛度Kp。

(4)由公式(2)得出全橋等效阻尼比，修正反應譜值，計算分析。

(5)將(4)計算出來的支座位移求得等效剛度，若誤差小于1.5%，迭代結束。

4 結 論

以多跨30 m簡支梁橋為背景，利用有限元軟件MIDAS Civil，基于新版抗規中的多振型反應譜迭代法進行分析，并與時程分析結果進行對比，得出以下結論：

(1)對于排架式橋墩的簡支梁橋，采用支座的等效剛度作為初始迭代剛度更加合理。

(2)不同墩高下，與時程法相比，修正反應譜法結果誤差基本上在20%以內，且大于時程法結果，在設計上偏安全。

(3)不同墩高下，支座的等效剛度變化不大；全橋等效阻尼比與剛度比的二次方相關。可假定支座的初始剛度為Keff=2.9 kN/mm，計算得出全橋等效阻尼比來修正反應譜值，減少迭代次數。

通過簡化反應譜方法可以對同類橋梁的減隔震設計進行計算，比時程分析法簡單，可靠度也較高。