給定觀測精度下的點(線)源模型重力與磁力橫向分辨能力研究

張義蜜， 王萬銀， 于長春， 熊盛青*

1 長安大學重磁方法技術(shù)研究所， 長安大學地質(zhì)工程與測繪學院， 長安大學西部礦產(chǎn)資源與地質(zhì)工程教育部重點實驗室， 西安 710054 2 中國自然資源航空物探遙感中心， 自然資源部航空地球物理與遙感地質(zhì)重點實驗室， 北京 100083

0 引言

在地球物理勘探中，重、磁勘探因具有效率高、成本低、工作范圍廣等優(yōu)點而受到重視(管志寧，2005；曾華霖，2005).但重、磁場具有疊加性，當相鄰有多個地質(zhì)體時，各個重、磁異常就可能會相互疊加，導致無法辨別重、磁異常是由單一地質(zhì)體還是由多個地質(zhì)體產(chǎn)生的(Gupta and Ramani，1982；Zeng et al.，1994；王寶仁和徐公達，1995)，這就需要對重力(重力異常、重力張量)和磁力(磁力異常、磁力張量)的理論橫向分辨能力以及在給定觀測精度下的實際橫向分辨能力進行研究.

對于重力異常的理論橫向分辨問題，前人研究結(jié)果(Fajklewicz，1976；王寶仁和徐公達，1995)表明對于兩個半徑相同的球體和水平圓柱體模型，同一埋深的重力異常可被理論橫向分辨的最小中心距分別為1倍和1.15倍埋深.對于重力垂直張量的理論橫向分辨問題研究較多(Elkins，1951；Hammer，1970；Butler，1984；王寶仁和徐公達，1995；徐公達，1986；徐公達等，1988；Li，2001a；Martinez and Li，2011；蔣甫玉等，2011；王浩然等，2013)，其他重力張量分量研究較少，王寶仁和徐公達(1995)給出了重力垂直張量對水平圓柱體模型的理論橫向分辨系數(shù)(即橫向分辨多個地質(zhì)體時最小中心距與埋深的比值)，其可理論橫向分辨的最小中心距為0.82倍埋深，其他學者僅給出了定性分析結(jié)果.王浩然等(2013)從反演的角度表明重力張量比重力異常具有更強的橫向分辨能力.重力位三階張量比二階張量、重力異常具有更強的橫向分辨能力，并且橫向分辨能力隨場源埋深的增大而減小(DiFrancesco et al.，2009；杜勁松和邱峰，2019).以上為前人對重力及重力張量理論橫向分辨能力的研究，但在給定觀測精度下重力及重力張量的實際橫向分辨能力研究則較少.徐公達等(1988)通過對重力垂直張量的實際橫向分辨能力研究得到，在重力垂直張量觀測精度為30E時，當幾個淺、小構(gòu)造中心距小于2倍埋深時，重力垂直張量將產(chǎn)生疊加，橫向上無法分辨.其他重力張量分量的實際橫向分辨能力則少有研究.

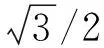
由此可知對于重力和磁力橫向分辨能力研究存在的問題為：(1)重力(重力異常、重力張量)、磁力(磁力異常、磁力張量)理論橫向分辨能力研究主要集中在重力異常和重力垂直張量，其他重力張量分量以及磁力研究較少；(2)前人研究結(jié)果大多沒有考慮觀測精度這一要素，缺乏實際橫向分辨能力研究結(jié)果.針對以上問題，本文以球體(點源模型)和無限延伸水平圓柱體(線源模型)重、磁場正演理論為基礎(chǔ)，詳細研究并對比了重力異常、重力張量、化極磁力異常以及垂直磁化磁力張量的理論橫向分辨能力和給定觀測精度下的實際橫向分辨能力.

1 重力異常及重力張量橫向分辨能力研究

重力異常與重力張量能夠分辨某一深度多個地質(zhì)體稱為重力異常與重力張量的橫向分辨能力.在理想觀測精度(觀測誤差為0)和給定觀測精度下，本文以球體(點源模型)和無限延伸水平圓柱體(線源模型)重力場正演理論為基礎(chǔ)研究重力異常與重力張量的橫向分辨能力.

1.1 重力異常及重力張量對球體模型橫向分辨能力研究

設(shè)兩個球體質(zhì)量分別為M和k·M(其中k為比例系數(shù)，k>0)，球體中心埋深均為D，沿x方向中心距為d.將坐標原點O選在兩個球心在地面的投影中心處，z坐標方向鉛垂向下為正，則兩個球體(圖1)在計算面(x,y,0)上引起的重力異常表達式為(索洛金，1955)

(1)

當兩個球體中心距較大時，其產(chǎn)生的重力異常有兩個極大值；中心距較小時，僅有一個極大值.隨著中心距由大到小，重力異常恰好有且僅有一個極大值時稱作重力異常理論上能橫向分辨兩個球體.

當兩個球體質(zhì)量相等時，可從剖面(x,0,0)上對重力異常理論橫向分辨能力進行研究.由(1)式可得，圖1所示球體模型在剖面(x,0,0)上引起的重力異常表達式為

(2)

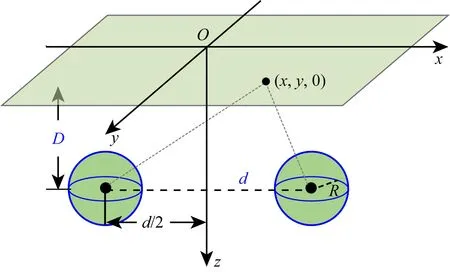
圖1 雙球體模型示意圖Fig.1 Schematic diagram of double sphere model

當中心距由大到小，剖面(x,0,0)上重力異常恰有一個極大值點時，中心距d和埋深D有以下關(guān)系(見附錄A)

d2-D2=0.

(3)

由(3)式得：d=1.0D.因此，重力異常能夠理論橫向分辨兩個等質(zhì)量球體時，理論橫向分辨系數(shù)(最小中心距與埋深比)為1.0，即最小中心距不能小于1.0倍埋深；由(3)式也可得到：D=1.0d，因此最大埋深不能超過1.0倍中心距.

在實際情況中，重力勘探具有一定的觀測精度.當兩個球體引起的重力異常極大值Δgmax與極小值Δgmin之差大于等于重力觀測精度時，兩個球體才能夠被分辨.即在給定觀測精度Δgmse下，兩個球體能被重力異常橫向分辨的臨界條件為

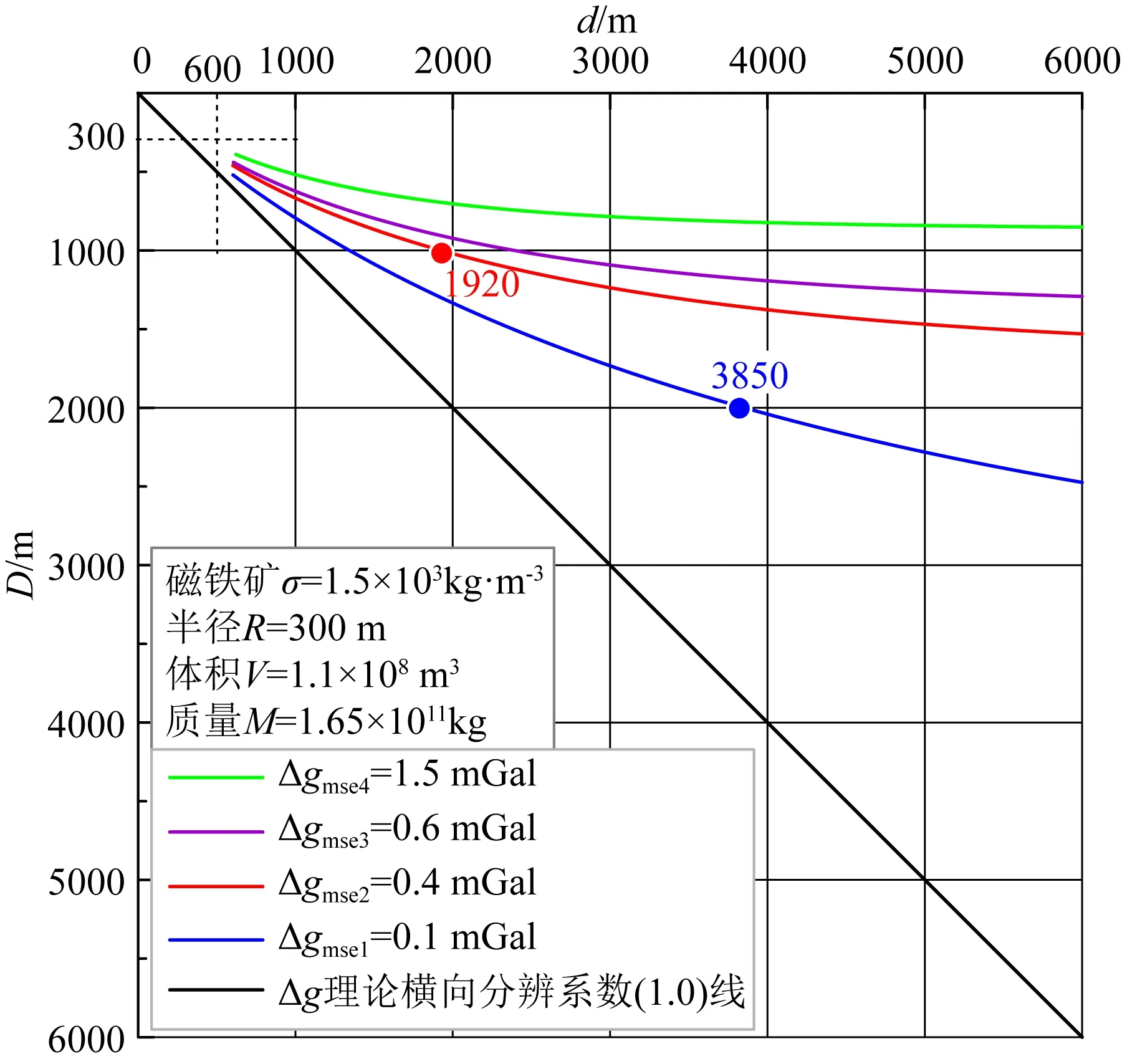
圖2 重力異常在不同觀測精度下的橫向分辨能力Fig.2 Lateral resolution of gravity anomaly under different survey accuracy

(4)

給定不同的重力觀測精度(0.1 mGal，0.4 mGal，0.6 mGal，1.5 mGal)并考慮垂向識別(張義蜜等，2020)基礎(chǔ)上，圖2為重力異常對等質(zhì)量的磁鐵礦(剩余密度取為1.5×103kg·m-3，半徑取為300 m，質(zhì)量為1.65×1011kg)的實際橫向分辨能力.從圖2可以得到，隨著重力觀測精度的提高，重力異常實際橫向分辨能力逐漸增強并接近理論分辨線.

利用上述方法同樣可以研究重力張量的橫向分辨能力.重力張量有9個分量，因為重力異常位滿足Laplace方程，而且Wxz和Wyz具有對稱性，所以只用研究Wxx、Wxy、Wxz和Wzz這4個分量的橫向分辨能力即可.

圖1所示球體模型重力張量表達式為(索洛金，1955)

(5)

由于(5)式中重力張量Wxx、Wxy、Wxz極值位置的解析解難以求解，故本文通過數(shù)值解研究這三個張量的理論橫向分辨能力.等質(zhì)量球體(k=1)引起的重力張量Wzz可通過解析解研究理論橫向分辨能力.

當兩球體質(zhì)量相等時，設(shè)球體半徑為100 m，剩余密度為1000 kg·m-3，埋深為200 m，中心距分別為6倍和1倍的埋深時，兩個球體在平面(x,y,0)上引起的重力張量Wxx、Wxy、Wxz如圖3所示.從圖3中可以看出，當兩個球體中心距較大時，重力張量Wxx、Wxy、Wxz分別有4、4、2個極大值；中心距較小時，分別有2、2、1個極大值.經(jīng)過極大值搜索技術(shù)(Blakely and Simpson,1986；王丁丁等，2021)得到當且僅當重力張量Wxx、Wxy、Wxz分別有2、2、1個極大值時，球體最小中心距與埋深有表1所示數(shù)值關(guān)系.

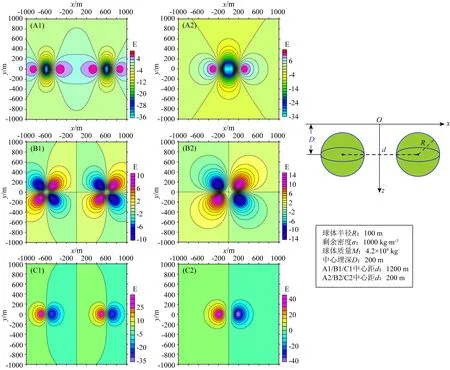
圖3 重力張量平面等值線圖(A1) 中心距為6倍埋深時Wxx等值線圖； (A2) 中心距為1倍埋深時Wxx等值線圖; (B1) 中心距為6倍埋深時Wxy等值線圖； (B2) 中心距為1倍埋深時Wxy等值線圖; (C1) 中心距為6倍埋深時Wxz等值線圖； (C2) 中心距為1倍埋深時Wxz等值線圖.Fig.3 Gravity tensor contour map(A1) Wxx contour map when center distance is 6 times buried depth; (A2) Wxx contour map when center distance is 1 times buried depth; (B1) Wxy contour map when center distance is 6 times buried depth; (B2) Wxy contour map when center distance is 1 times buried depth; (C1) Wxz contour map when center distance is 6 times buried depth; (C2) Wxz contour map when center distance is 1 times buried depth.

表1 三個重力張量Wxx、Wxy、Wxz最小中心距與埋深的關(guān)系Table 1 Relationship between minimum center distance and buried depth of three gravity tensors Wxx, Wxy, Wxz

將表1數(shù)據(jù)繪圖并線性擬合如圖4所示，重力張量Wxx、Wxy、Wxz的理論橫向分辨系數(shù)(最小中心距與埋深比)分別為0.723、1.0和1.0.即重力張量Wxx、Wxy、Wxz橫向分辨兩個等質(zhì)量球體時，最小中心距不能小于0.723、1.0和1.0倍埋深.

當兩個球體質(zhì)量相等時，可從剖面(x,0,0)上對重力張量Wzz(x,0,0)的理論橫向分辨能力進行研究.圖1所示球體模型在剖面(x,0,0)上引起的重力張量Wzz(x,0,0)表達式為(索洛金，1955)

Wzz(x,0,0)=G·M·

(6)

當中心距由大到小，剖面(x,0,0)上重力張量Wzz(x,0,0)恰有一個極大值點時，中心距d和埋深D有以下關(guān)系(見附錄B)

d6-43d4D2+448d2D4-256D6=0.

(7)

由(7)式得：d=0.778D.因此，重力張量Wzz能夠橫向分辨兩個等質(zhì)量球體時，理論橫向分辨系數(shù)(最小中心距與埋深比)為0.778，即最小中心距不能小于0.778倍埋深.

當兩個球體質(zhì)量比k≥1時，重力及其張量理論橫向分辨系數(shù)與球體質(zhì)量比(k)的關(guān)系如表2所示.

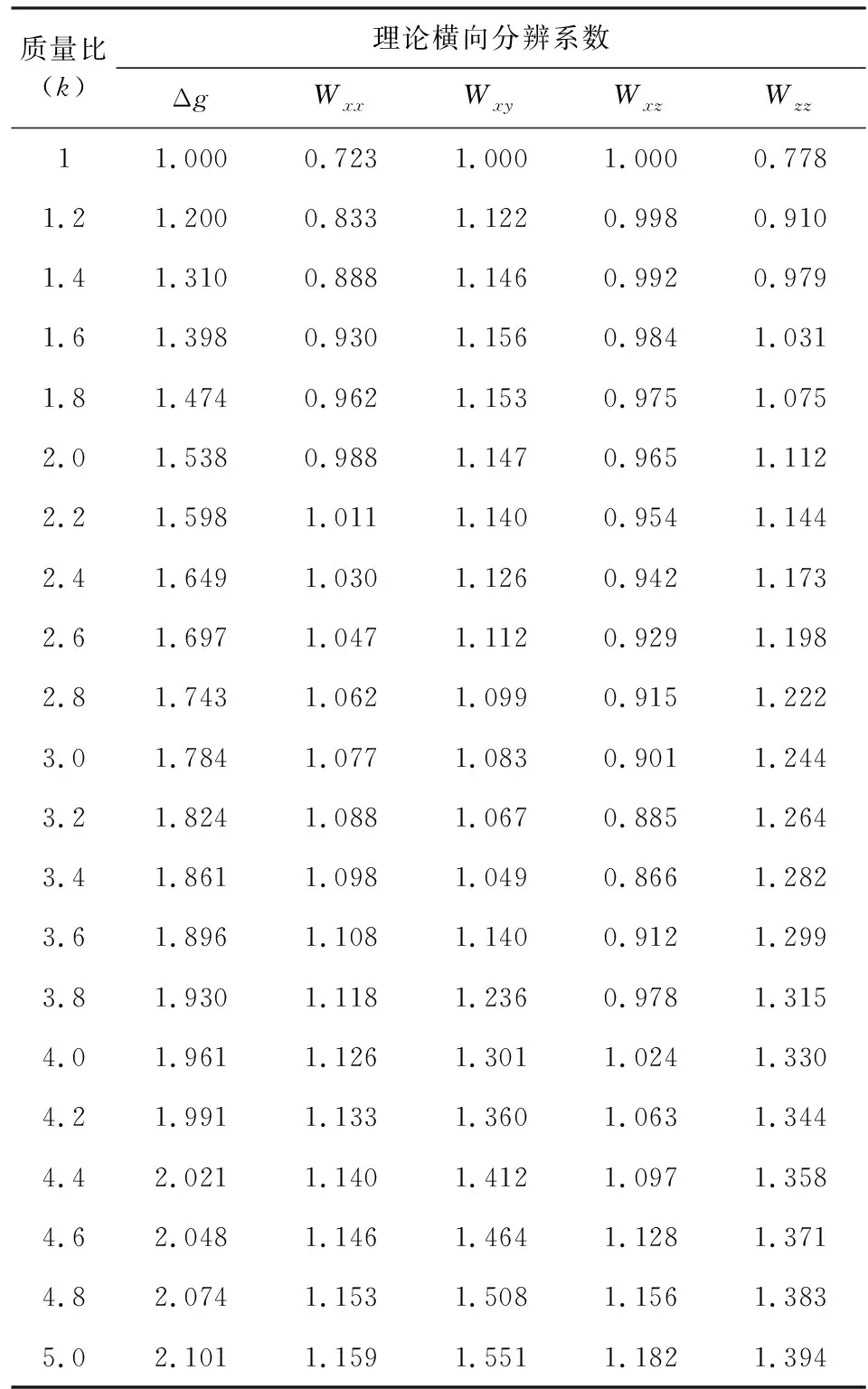
表2 重力異常Δg及重力張量Wxx、Wxy、Wxz、Wzz理論橫向分辨系數(shù)與球體質(zhì)量比(k)的關(guān)系Table 2 Relationship between the theoretical lateral resolution coefficients of gravity anomaly Δg gravity tensors Wxx, Wxy, Wxz and Wzz and the mass ratio (k) of the sphere

取等質(zhì)量的球體和直立六面體模型，剩余密度均取為1000 kg·m-3，以重力垂直張量Wzz為例研究其對不同模型的理論橫向分辨能力(表3).

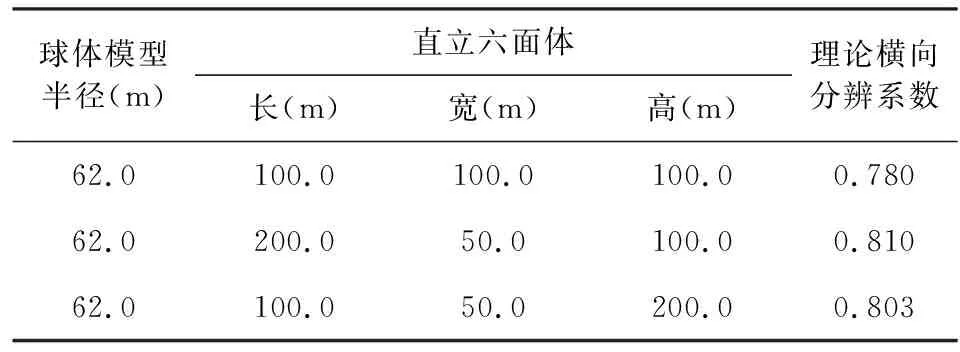
表3 等質(zhì)量球體和直立六面體模型重力張量Wzz理論橫向分辨系數(shù)Table 3 Gravity tensor Wzz theory lateral resolution coefficient of equal mass sphere and vertical hexahedron model

從表3可以看出，重力張量Wzz對等質(zhì)量的球體和直立六面體理論橫向分辨能力隨著直立六面體的長寬高變化有著輕微變化，但系數(shù)與雙球體理論橫向分辨系數(shù)0.778相差不大(相對均方根約為4.1%)，因此可以認為重力張量Wzz理論橫向分辨能力對非點源體也有一定的適應性.

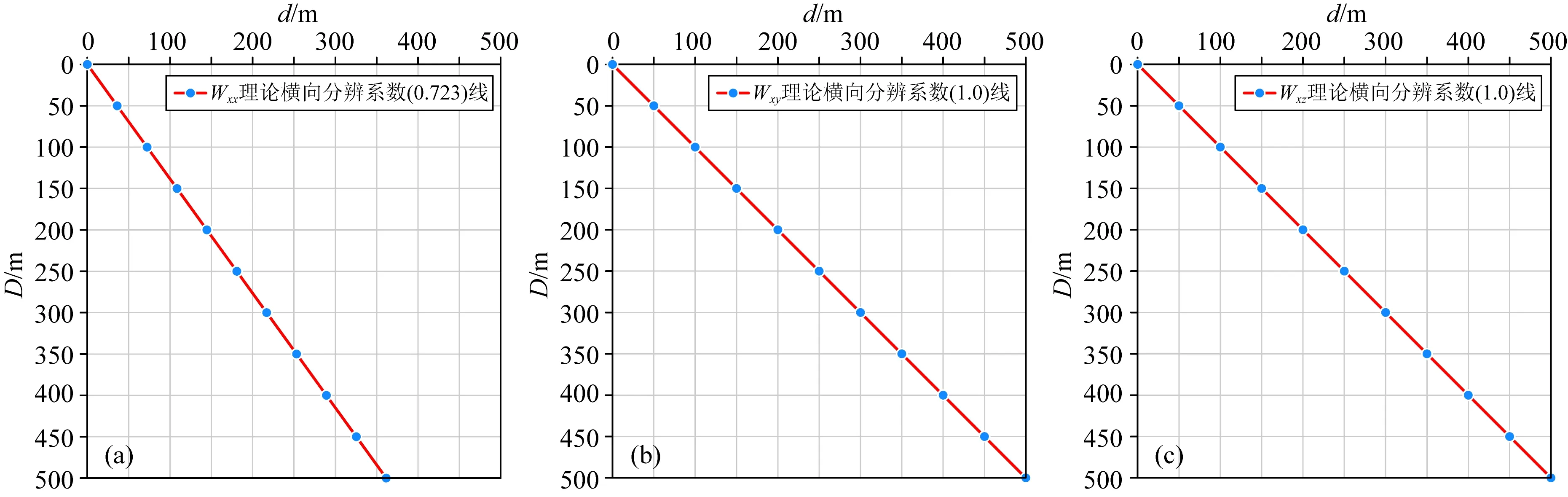
圖4 三個重力張量Wxx、Wxy、Wxz中心距與埋深的關(guān)系(a) Wxx； (b) Wxy； (c) Wxz.Fig.4 Relationship between the center distance and buried depth of three gravity tensors Wxx, Wxy, Wxz

根據(jù)重力異常實際橫向分辨能力研究思路，在現(xiàn)有的重力觀測精度(重力異常觀測精度取為0.1 mGal、重力張量觀測精度取為10E)和垂向識別基礎(chǔ)上，研究并對比重力異常和重力張量Wxx、Wxy、Wxz以及Wzz對等質(zhì)量的磁鐵礦(剩余密度取為1.5×103kg·m-3、半徑取為300 m，質(zhì)量為1.65×1011kg)的實際橫向分辨能力.

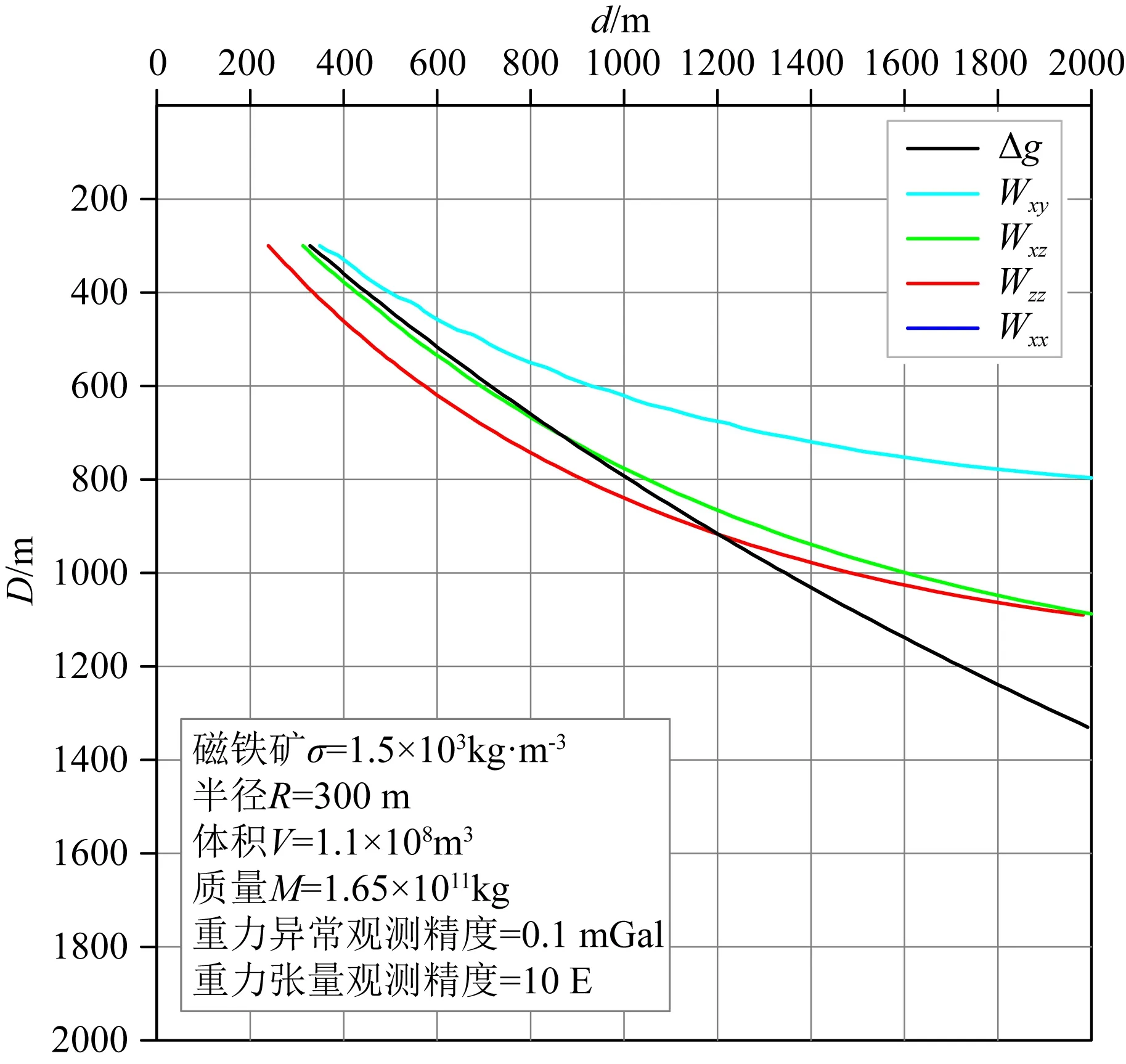
圖5 重力異常與重力張量橫向分辨能力對比Fig.5 Comparison of the lateral resolution between gravity anomaly and gravity tensor

根據(jù)圖5可知，重力異常及重力張量實際橫向分辨曲線隨埋深增加呈指數(shù)衰減，重力張量Wxx和Wzz橫向分辨能力基本相同，Wxz略次之，Wxy最弱.在800 m以淺，重力異常和重力張量Wxz實際橫向分辨能力幾乎相同，在800 m以深，重力異常實際橫向分辨能力優(yōu)于重力張量Wxz.在900 m以淺，重力異常實際橫向分辨能力弱于重力張量Wxx和Wzz，在900 m以深，則相反.

1.2 重力異常及重力張量對無限延伸水平圓柱體模型橫向分辨能力研究

設(shè)兩個半徑、剩余密度均相等的水平圓柱體(圖6)沿y方向無限延伸，中軸線埋深為D，中心距為d，半徑為R(R≤D)，線密度為λ.將坐標原點O選在兩條中軸線在地面投影中心處，且讓y軸平行中軸線，z坐標方向鉛垂向下為正，則x軸上任意點(x,0)處的重力異常表達式為(索洛金，1955)

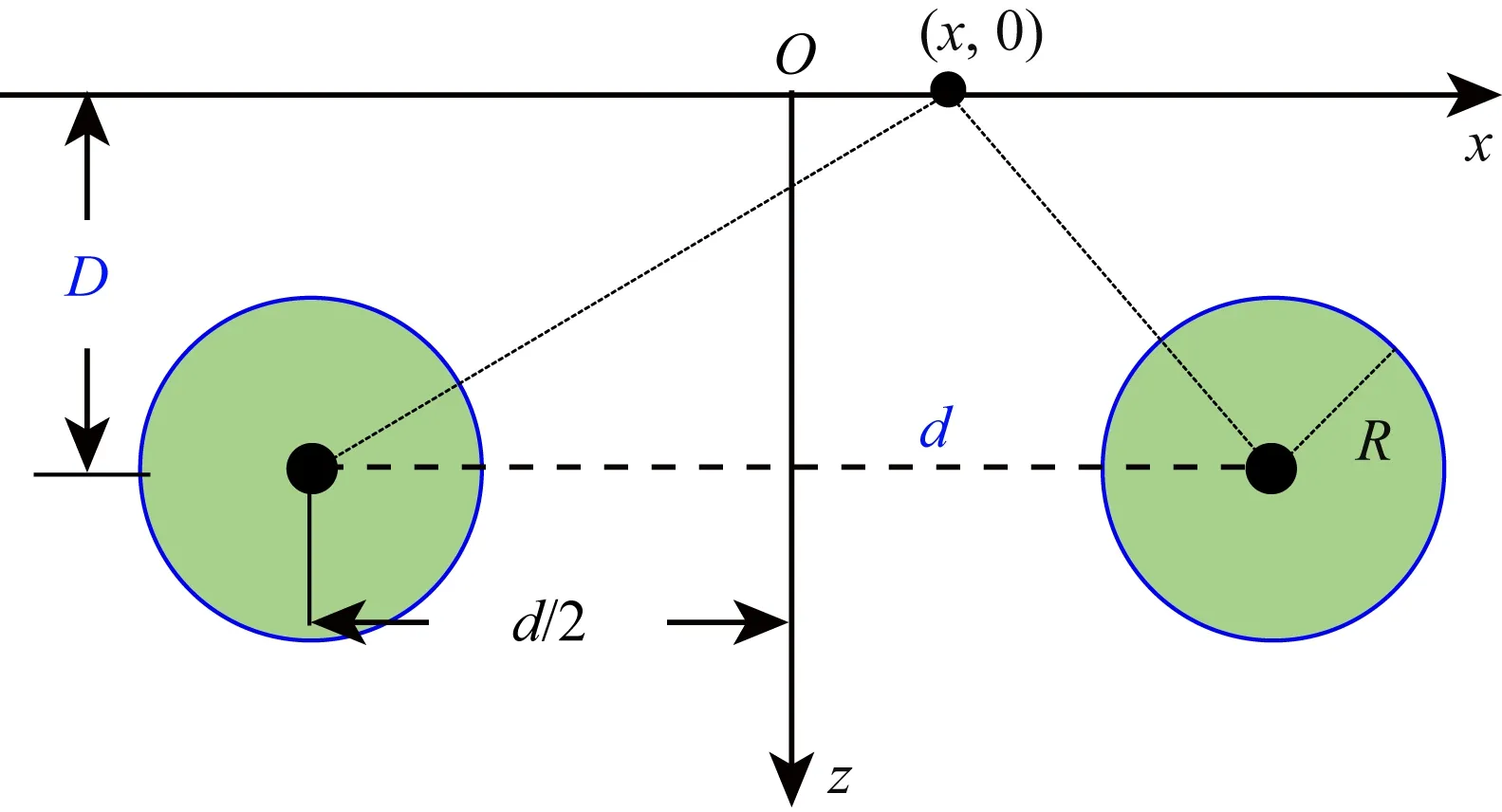
圖6 雙無限延伸水平圓柱體模型示意圖Fig.6 Schematic diagram of double infinitely extending horizontal cylinder model

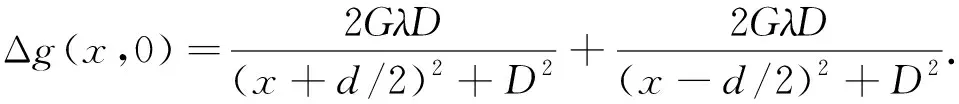
(8)

對重力異常Δg(x,0)沿x方向求導，可得

?Δg(x,0)/?x=

(9)

令?Δg(x,0)/?x=0，解方程得(別列茲金，1994)

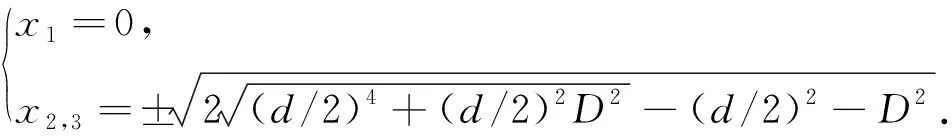
(10)

重力異常理論橫向分辨兩個無限延伸水平圓柱體的臨界條件是：重力異常有且僅有一個極大值，由(10)式可得

(11)

圖6所示無限延伸水平圓柱體引起的重力張量表達式為(索洛金，1955)

(12)

由于(12)式中重力張量Wxz極值位置的解析解難以求解，故本文通過數(shù)值解研究重力張量Wxz的理論橫向分辨能力.重力張量Wzz可通過解析解研究理論橫向分辨能力.

設(shè)水平圓柱體半徑為100 m，剩余密度為1000 kg·m-3，兩個水平圓柱體中心埋深為400 m，中心距分別為2倍、0.25倍中心埋深時，產(chǎn)生的重力張量Wxz(x,0)如圖7所示.從圖7中可以看出，當兩個水平圓柱體中心距較大時，重力張量Wxz有2個極大值；中心距較小時，有1個極大值.經(jīng)過極大值搜索技術(shù)(Blakely and Simpson,1986；王丁丁等，2021)得到當且僅當重力張量Wxz有1個極大值時，水平圓柱體最小中心距與埋深有表4所示數(shù)值關(guān)系.

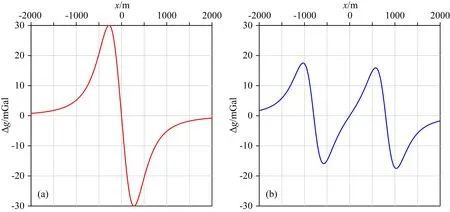
圖7 重力張量Wxz異常曲線圖(a) 中心距為2倍埋深的Wxz異常曲線; (b) 中心距為0.25倍埋深的Wxz異常曲線.Fig.7 Gravity tensor Wxz curve graph(a) Wxz curve graph when center distance is 2 times buried depth; (b) Wxz curve graph when center distance is 0.25 times buried depth.

表4 重力張量Wxz最小中心距與埋深的關(guān)系Table 4 Relationship between minimum center distance and buried depth of gravity tensor Wxz

將表4數(shù)據(jù)繪圖并線性擬合如圖8所示，重力張量Wxz的理論橫向分辨系數(shù)(最小中心距與埋深比)為1.115.即重力張量Wxz橫向分辨兩個無限延伸水平圓柱體時，最小中心距不能小于1.115倍埋深.

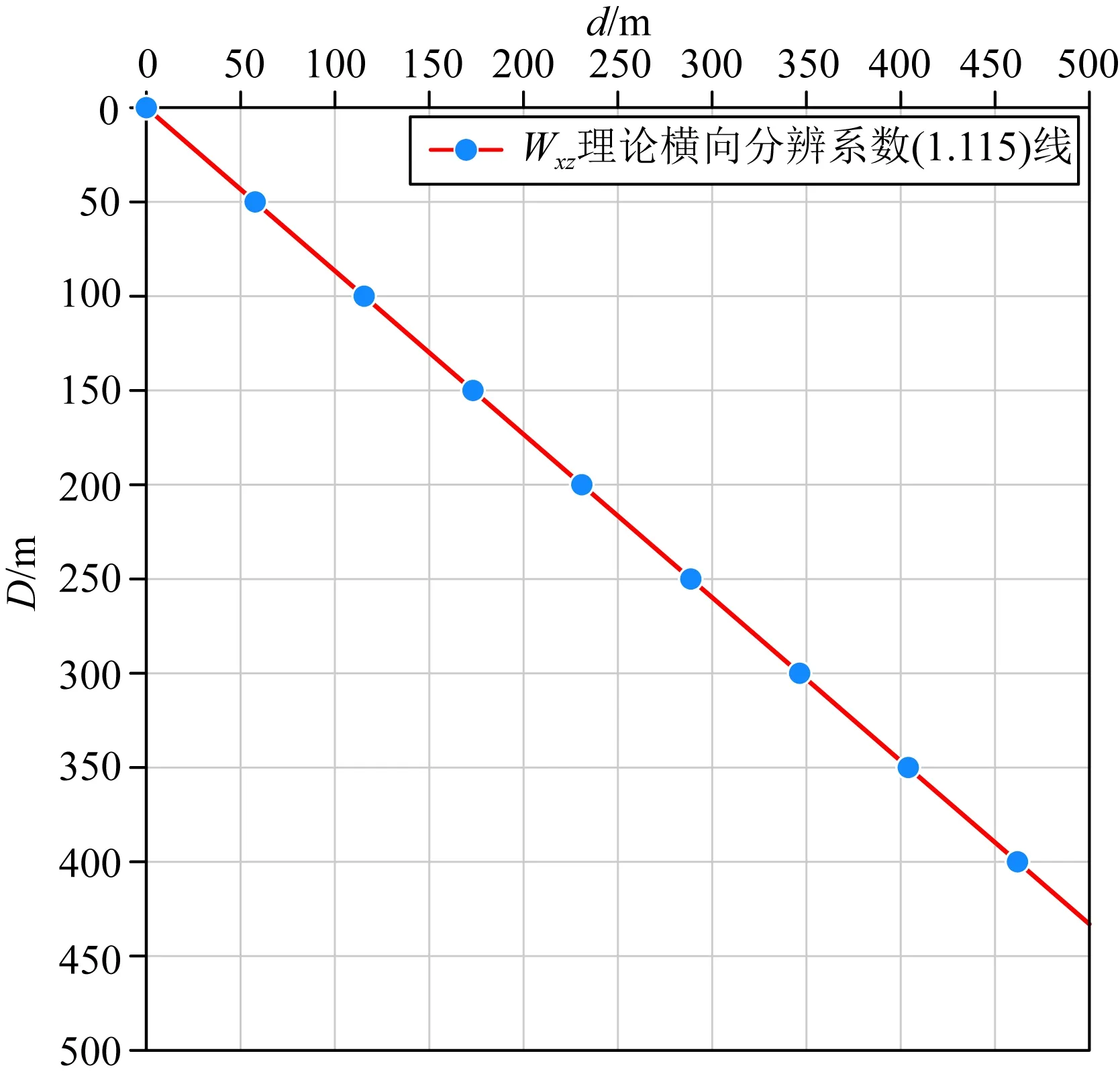
圖8 重力張量Wxz中最小中心距與埋深的關(guān)系Fig.8 The relationship between minimum center distance and buried depth of gravity tensor Wxz

對于重力張量Wzz可從解析解得出理論橫向分辨能力.當中心距由大到小，剖面(x,0)上重力張量Wzz(x,0)恰有一個極大值點時，有以下關(guān)系

d8-16d6D2-160d4D4-256d2D6+256D8=0,

(13)

2 磁力異常及磁力張量橫向分辨能力研究

磁力異常與磁力張量能夠分辨某一深度多個地質(zhì)體稱為磁力異常與磁力張量的橫向分辨能力.在理想觀測精度(觀測誤差為0)和實際觀測精度下，本文以球體(點源模型)和無限延伸水平圓柱體(線源模型)重力場正演理論為基礎(chǔ)研究磁力異常與磁力張量的橫向分辨能力.

2.1 磁力異常及磁力張量對球體模型橫向分辨能力研究

磁力異常與磁傾角和磁偏角相關(guān)，不易直接用來研究橫向分辨能力.實際磁力數(shù)據(jù)處理、解釋中常用化極磁力異常、垂直磁化磁力張量，因此需要研究化極磁力異常、垂直磁化磁力張量的橫向分辨能力.

設(shè)兩個球體磁矩大小分別為m和k·m(其中k為比例系數(shù)，k>0)，球體中心埋深均為D，沿x方向中心距為d.將坐標原點O選在兩個球心在地面投影中心處，z坐標方向鉛垂向下為正，則兩個球體在計算面(x,y,0)上引起的化極磁力異常為(考留巴金和拉賓娜，1963)

(14)

兩個球體引起的化極磁力異常公式與重力垂直梯度公式相似，僅是系數(shù)(常數(shù))的差別.因此，化極磁力異常具有和重力垂直梯度相同的理論橫向分辨能力.化極磁力異常能夠分辨兩個相等磁矩的球體時，理論橫向分辨系數(shù)也為0.778，最小中心距不能小于0.778倍埋深.

按照重力異常實際橫向分辨能力研究思路，在現(xiàn)有的磁力觀測精度(磁力觀測精度取為±4.0 nT和±2.0 nT)和垂向識別基礎(chǔ)上，研究化極磁力異常對磁鐵礦(磁化強度取為66.0 A·m-1、半徑取為300 m，磁矩大小為7.26×109A·m2)和矽卡巖(磁化強度取為0.8 A·m-1、半徑取為300 m，磁矩大小為8.8×107A·m2)的實際橫向分辨能力.

從圖9可以得到：化極磁力異常對磁鐵礦的實際橫向分辨能力強于矽卡巖；隨著觀測精度地提高，化極磁力異常的實際橫向分辨能力也逐漸增強.

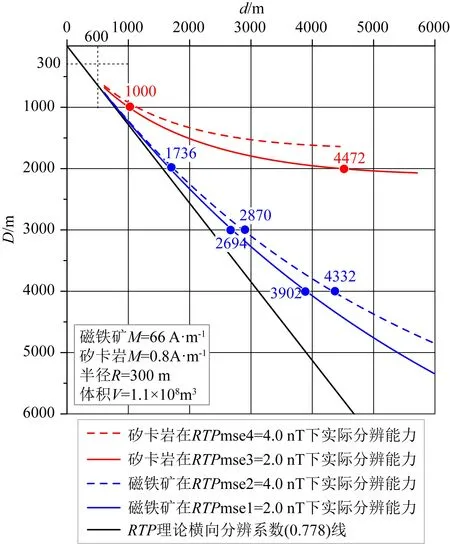
圖9 化極磁力異常對不同地質(zhì)體的橫向分辨能力Fig.9 Lateral resolution of RTP for different geological bodies

利用上述方法同樣可以研究垂直磁化磁力張量的橫向分辨能力.垂直磁化磁力張量共有9個分量，因為磁力異常位滿足Laplace方程，而且Uxz和Uyz具有對稱性，所以只需要研究Uxx、Uxy、Uxz、Uzz這4個分量的橫向分辨能力即可.

圖1所示球體模型垂直磁化磁力張量表達式為(秦葆瑚，1980)

(15)

由于(15)式中垂直磁化磁力張量Uxx、Uxy、Uxz極值位置的解析解難以求解，故本文通過數(shù)值解研究這三個垂直磁化磁力張量的理論橫向分辨能力.等磁矩球體(k=1)引起的垂直磁化磁力張量Uzz可通過解析解研究理論橫向分辨能力.

設(shè)等磁矩球體半徑為100 m，磁化強度為0.1 A·m-1，兩個球體埋深為200 m，球體中心距分別為6倍和0.6倍的中心埋深時，兩個球體在平面(x,y,0)上引起的垂直磁化磁力張量Uxx、Uxy、Uxz如圖10所示.從圖10可以看出，當兩個球體中心距較大時，垂直磁化磁力張量Uxx、Uxy、Uxz分別有4、4、2個極大值；中心距較小時，分別有2、2、1個極大值.經(jīng)過極大值搜索技術(shù)(Blakely and Simpson,1986；王丁丁等，2021)得到當且僅當垂直磁化磁力張量Uxx、Uxy、Uxz分別有2、2、1個極大值時，最小中心距與埋深有表5所示數(shù)值關(guān)系.

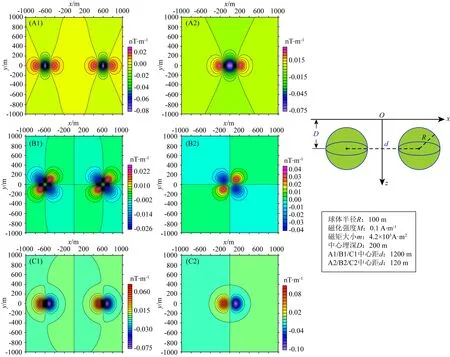
圖10 垂直磁化磁力張量平面等值線圖(A1) 中心距為6倍埋深時Uxx等值線圖； (A2) 中心距為0.6倍埋深時Uxx等值線圖; (B1) 中心距為6倍埋深時Uxy等值線圖； (B2) 中心距為0.6倍埋深時Uxy等值線圖; (C1) 中心距為6倍埋深時Uxz等值線圖； (C2) 中心距為0.6倍埋深時Uxz等值線圖.Fig.10 Vertical magnetization magnetic tensor contour map(A1) Uxx contour map when center distance is 6 times buried depth; (A2) Uxx contour map when center distance is 0.6 times buried depth; (B1) Uxy contour map when center distance is 6 times buried depth; (B2) Uxy contour map when center distance is 0.6 times buried depth; (C1) Uxz contour map when center distance is 6 times buried depth; (C2) Uxz contour map when center distance is 0.6 times buried depth.

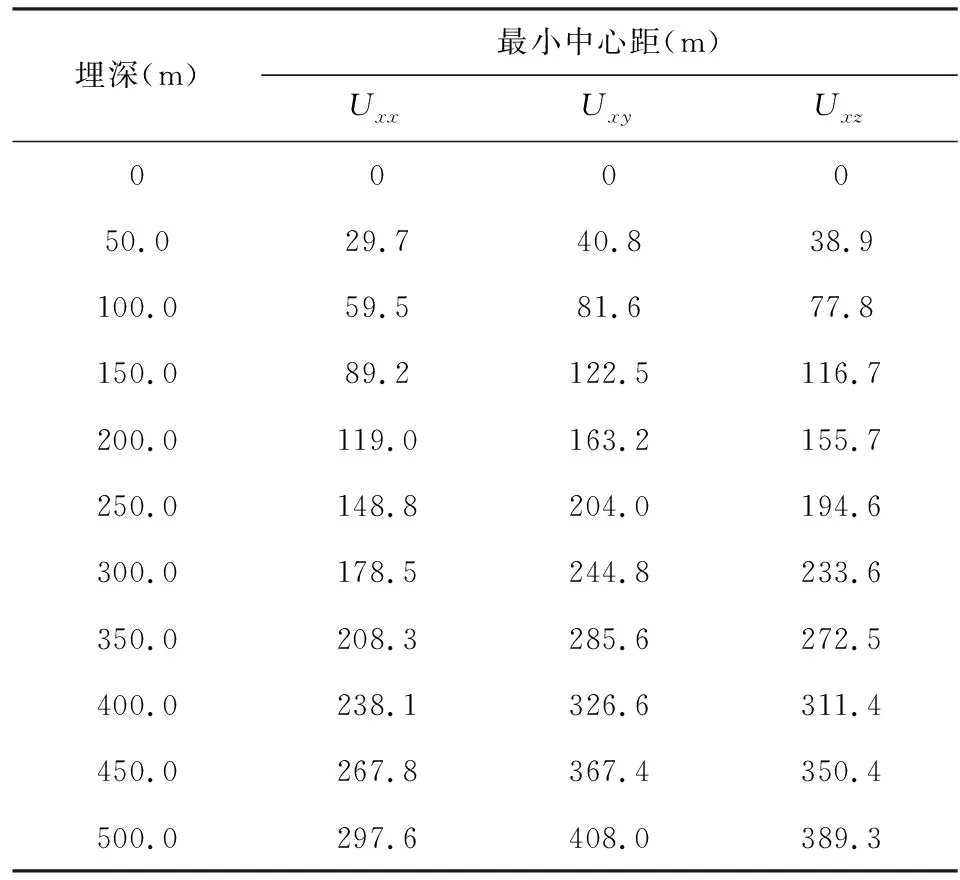
表5 垂直磁化磁力張量Uxx、Uxy、Uxz最小中心距與埋深的關(guān)系Table 5 Relationship between minimum center distance and buried depth vertical magnetization magnetic tensor Uxx, Uxy, Uxz

將表5數(shù)據(jù)繪圖并線性擬合如圖11所示，垂直磁化磁力張量Uxx、Uxy、Uxz的理論橫向分辨系數(shù)分別為0.595、0.816和0.778.即垂直磁化磁力張量Uxx、Uxy、Uxz橫向分辨兩個球體時，最小中心距不能小于0.595、0.816和0.778倍埋深.

從平面(x,y,0)上不易對垂直磁化磁力張量Uzz橫向分辨能力進行理論研究，故在剖面(x,0,0)上研究.圖1所示球體模型在剖面(x,0,0)上引起的垂直磁化磁力張量Uzz(x,0,0)表達式為(秦葆瑚，1980)

(16)

當中心距由大到小，剖面(x,0,0)上垂直磁化磁力Uzz(x,0,0)恰有一個極大值點時，有以下關(guān)系

27d6-390d4D2+1408d2D4-512D6=0.

(17)

由(17)式得：d=0.639D.因此，垂直磁化磁力張量Uzz能夠橫向分辨兩個球體時，理論橫向分辨系數(shù)為0.639，即最小中心距不能小于0.639倍埋深.

當兩個球體質(zhì)量比k≥1時，化極磁力異常及垂直磁化磁力張量理論橫向分辨系數(shù)與球體質(zhì)量比(k)的關(guān)系如表6所示.

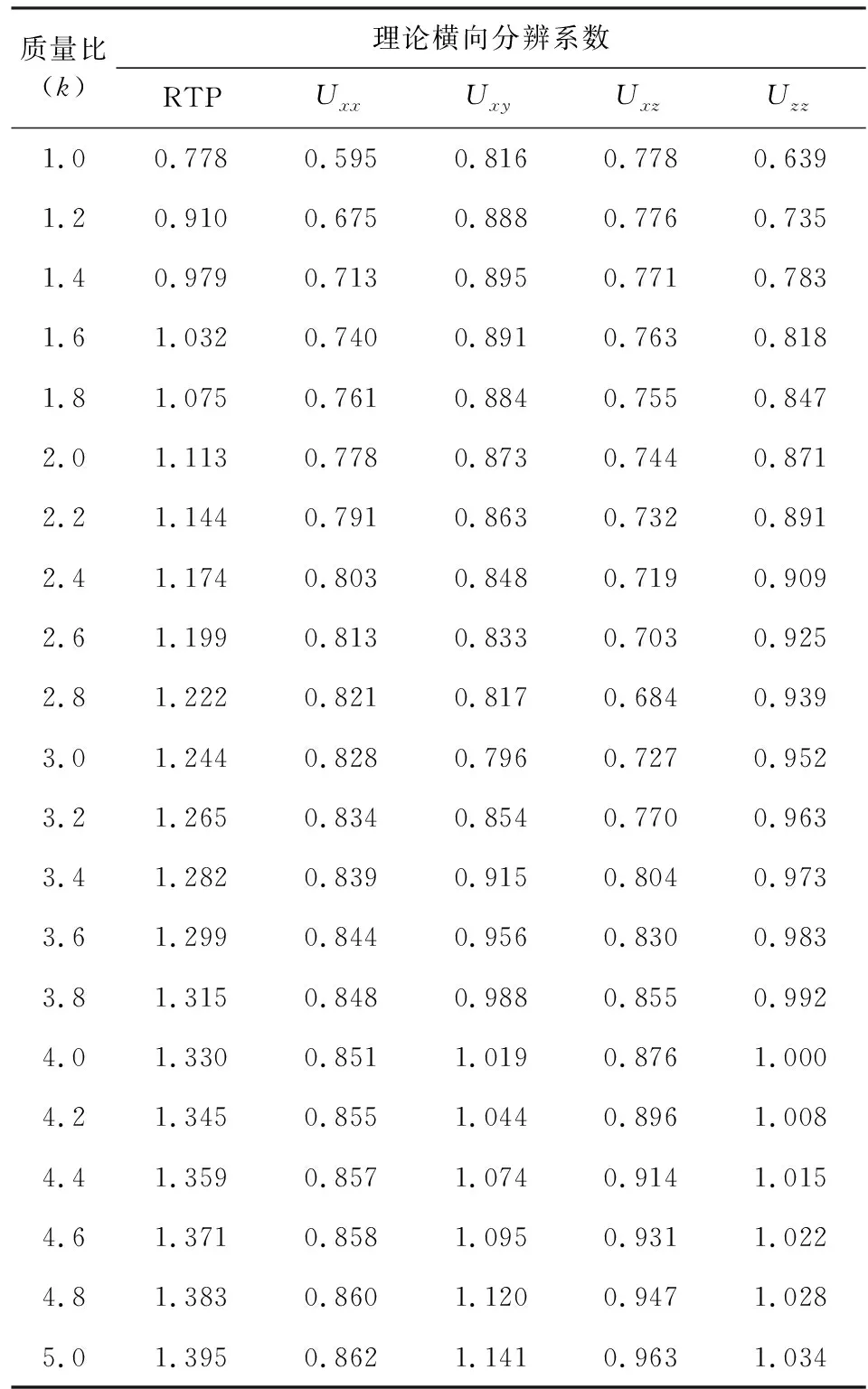
表6 化極磁力異常RTP及垂直磁化磁力張量Uxx、Uxy、Uxz、Uzz理論橫向分辨系數(shù)與球體質(zhì)量比(k)的關(guān)系

實際情況中，化極磁力異常和垂直磁化磁力張量觀測具有一定的觀測精度.在現(xiàn)有的磁力異常觀測精度(化極磁力異常取為2 nT、磁力張量觀測精度取為±0.04 nT)和垂向識別基礎(chǔ)上，研究化極磁力異常和垂直磁化磁力張量Uxx、Uxy、Uxz以及Uzz對磁鐵礦(磁化強度取為66.0 A·m-1、半徑取為300 m，磁矩為7.26×109A·m2)的實際橫向分辨能力.

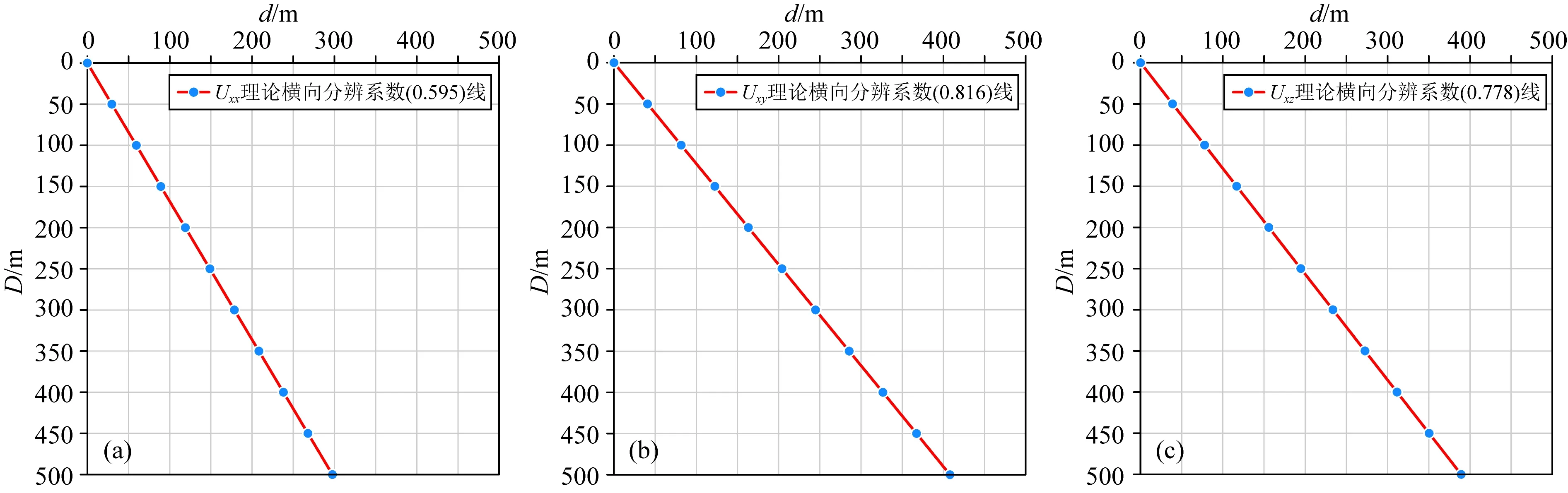
圖11 垂直磁化磁力張量三個分量Uxx、Uxy、Uxz中心距與埋深的關(guān)系(a) Uxx； (b) Uxy； (c) Uxz.Fig.11 Relationship between center distance and buried depth of vertical magnetization magnetic tensor Uxx, Uxy, Uxz

根據(jù)圖12可知，化極磁力異常和垂直磁化磁力張量實際橫向分辨曲線隨埋深增加呈指數(shù)衰減，垂直磁化磁力張量Uxx和Uzz橫向分辨能力基本相同，Uxz略次之，Uxy最弱.在1200 m以淺，化極磁力異常和垂直磁化磁力張量Uxz實際橫向分辨能力幾乎相同，在1200 m以深，化極磁力異常實際橫向分辨能力優(yōu)于垂直磁化磁力張量Uxz.在2200 m以淺，化極磁力異常實際橫向分辨能力弱于垂直磁化磁力張量Uxx和Uzz，在2200 m以深，則相反.

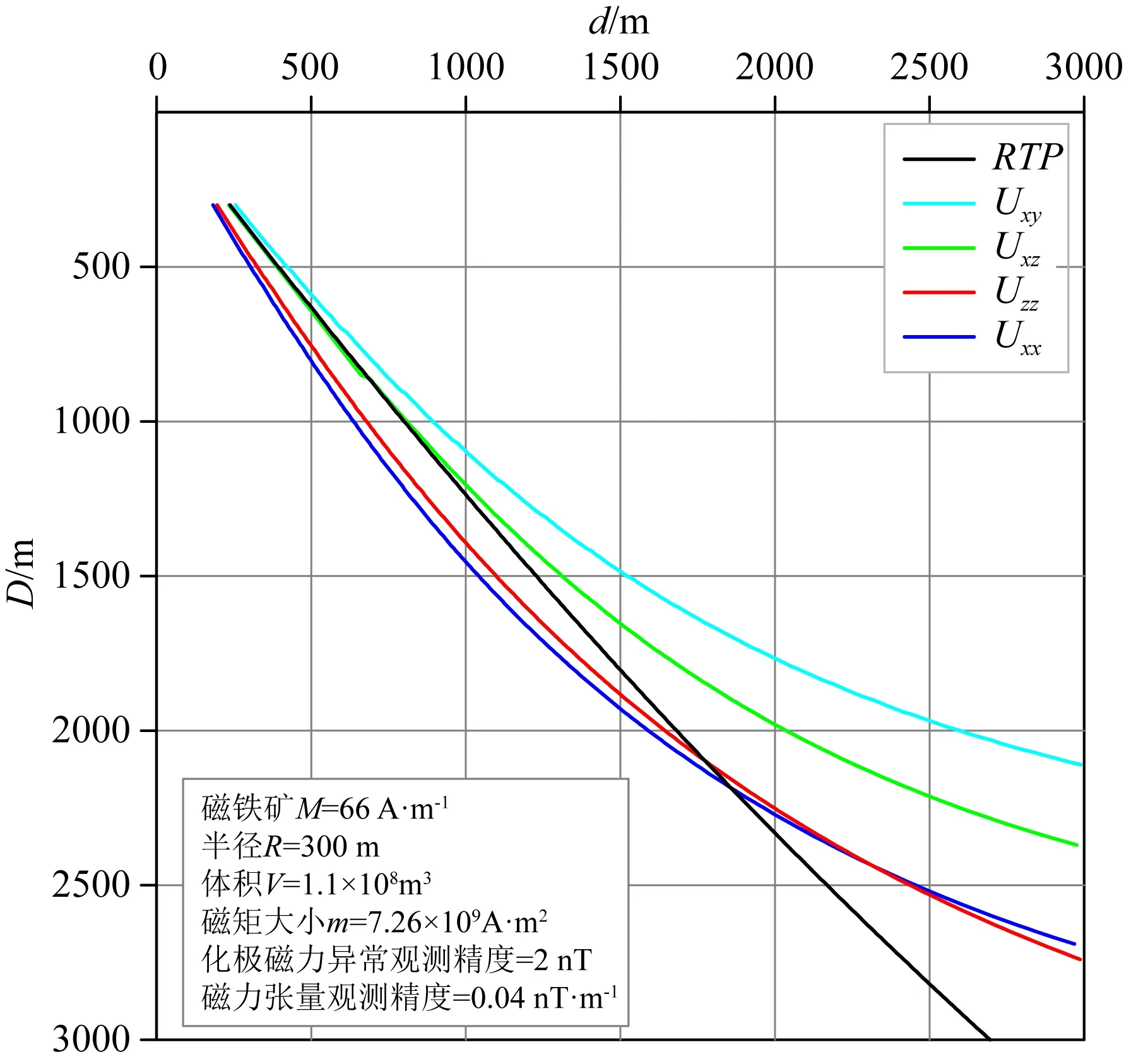
圖12 化極磁力異常與垂直磁化磁力張量橫向分辨能力對比Fig.12 Comparison of the lateral resolution between RTP and vertical magnetization magnetic tensor

2.2 磁力異常及磁力張量對無限延伸水平圓柱體模型橫向分辨能力研究

設(shè)兩個半徑、磁化強度相等的水平圓柱體沿y方向無限延伸，中軸線埋深為D，半徑為R(R≤D)，磁化強度為M.將坐標原點O選在兩條中軸線在地面投影中心處，且讓y軸平行中軸線，z坐標鉛垂向下為正，則x軸上任意點(x,0)處化極磁力異常表達式為(考留巴金和拉賓娜，1963)

(18)

兩個水平圓柱體化極磁力異常公式和重力異常垂直梯度公式相似，僅是系數(shù)(常數(shù))的差別.因此，化極磁力異常具有和重力異常垂直梯度相同的橫向分辨能力.化極磁力異常能夠分辨兩個無限延伸水平圓柱體時，理論橫向分辨系數(shù)為0.828，即最小中心距不能小于0.828倍埋深.

圖6所示無限延伸水平圓柱體引起的垂直磁化磁力張量表達式為(秦葆瑚，1980)

(19)

由于(19)式中垂直磁化磁力張量Uxz極值位置的解析解難以求解，故本文通過數(shù)值解研究垂直磁化磁力張量Uxz的理論橫向分辨能力.垂直磁化磁力張量Uzz可通過解析解研究理論橫向分辨能力.

設(shè)無限延伸水平圓柱體半徑為100m，磁化強度為4.0 A·m-1，埋深為400 m，中心距分別為2倍、0.25倍中心埋深時，產(chǎn)生的垂直磁化磁力張量Uxz(x,0)如圖13所示.從圖13中可以看出，當兩個水平圓柱體中心距較大時，垂直磁化磁力張量Uxz有2個極大值；中心距較小時，有1個極大值.經(jīng)過極大值搜索技術(shù)(Blakely and Simpson,1986)得到當且僅當垂直磁化磁力張量Uxz有1個極大值時，水平圓柱體最小中心距與埋深有表7所示數(shù)值關(guān)系.

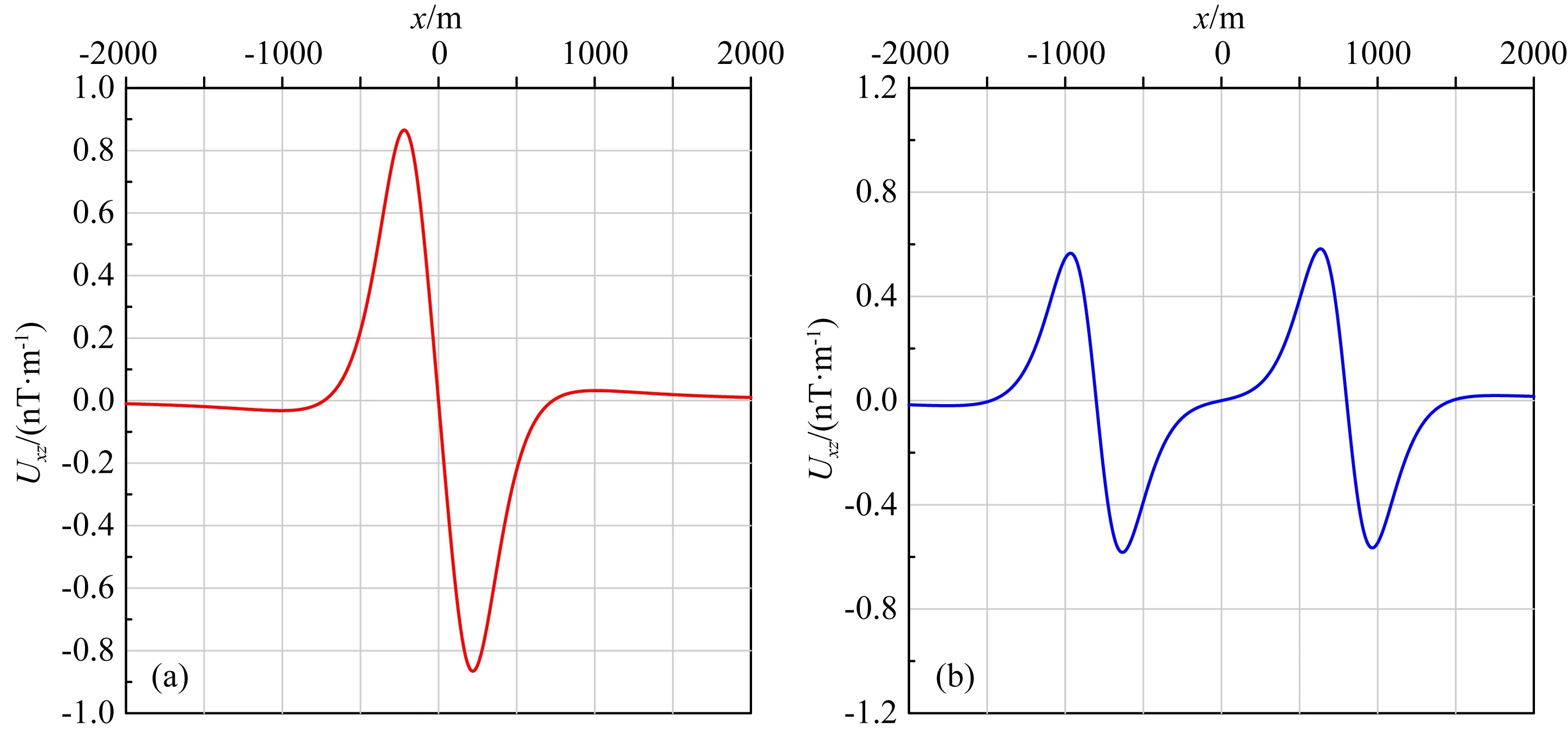
圖13 垂直磁化磁力張量Uxz異常曲線圖(a) 中心距2倍埋深的Uxz異常曲線； (b) 中心距0.25倍埋深的Uxz異常曲線.Fig.13 Vertical magnetization magnetic tensor Uxz curve graph(a) Uxz graph when center distance is 2 times buried depth; (b) Uxz graph when center distance is 0.25 times buried depth.

將表7數(shù)據(jù)繪圖并線性擬合如圖14所示，垂直磁化磁力張量Uxz的理論橫向分辨系數(shù)為0.828.即垂直磁化磁力張量Uxz橫向分辨兩個無限延伸水平圓柱體時，最小中心距不能小于0.828倍埋深.

表7 垂直磁化磁力張量Uxz最小中心距與埋深的關(guān)系Table 7 Relationship between minimum center distance and buried depth of vertical magnetization magnetic tensor Uxz

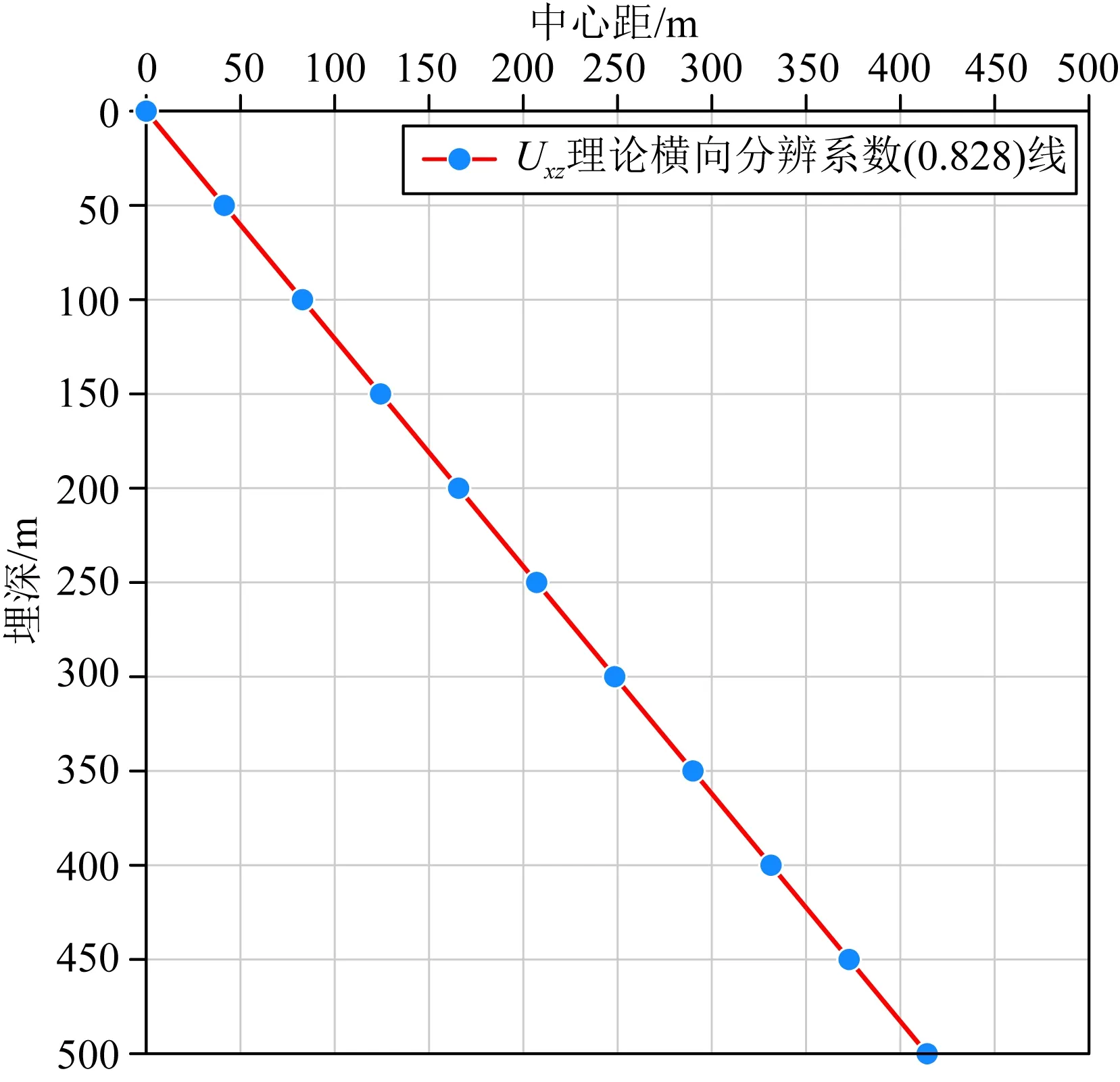
圖14 垂直磁化磁力張量Uxz最小中心距與埋深的關(guān)系Fig.14 The relationship between minimum center distance and buried depth of vertical magnetization magnetic tensor Uxz

對于垂直磁化磁力張量Uzz(x,0)可從解析解得出理論橫向分辨能力.當中心距由大到小，剖面(x,0)上垂直磁化磁力張量Uzz(x,0)恰有一個極大值點時，有以下關(guān)系

5d4-40d2D2+16D4=0,

(20)

由式(20)得：d=0.649D.因此，垂直磁化磁力張量Uzz能夠分辨兩個無限延伸水平圓柱體時，理論橫向分辨系數(shù)為0.649，即最小中心距不能小于0.649倍埋深.

3 重力、磁力及其張量橫向分辨能力對比研究

3.1 重力、磁力及其張量對球體模型橫向分辨能力對比研究

本文通過理論橫向分辨系數(shù)(最小中心距與埋深比)大小來衡量重力和磁力的理論橫向分辨能力強弱，系數(shù)越大代表理論橫向分辨能力越弱；系數(shù)越小則表示理論橫向分辨能力越強，表8是重力異常、重力張量、化極磁力異常以及垂直磁化磁力張量對等質(zhì)量球體模型的理論橫向分辨系數(shù).

從表8可以得到：重力異常、重力張量、化極磁力異常以及垂直磁化磁力張量對于等質(zhì)量球體(點源模型)的理論橫向分辨能力由強到弱依次為：Uxx>Uzz>Uxz=RTP>Uxy>Wxx>Wzz>Wxz=Wxy=Δg.

表8 重力異常、重力張量、化極磁力異常以及垂直磁化磁力張量理論橫向分辨系數(shù)(球體模型)Table 8 Theoretical lateral resolution coefficient of gravity anomaly, gravity tensor, reduction to the pole (RTP) of magnetic anomaly, vertical magnetization magnetic tensor (sphere model)

在現(xiàn)有的重力觀測精度(重力觀測精度取為±0.4 mGal和±0.1 mGal)和磁力觀測精度(磁力觀測精度取為±4.0 nT和±2.0 nT)以及垂向識別基礎(chǔ)上，對比球體賦存磁鐵礦(剩余密度取為1.5×103kg·m-3，磁化強度取為66.0 A·m-1，半徑取為300 m，質(zhì)量為1.65×1011kg，磁矩大小為7.26×109A·m2)和賦存矽卡巖(剩余密度取為0.24×103kg·m-3，磁化強度取為0.8A·m-1，半徑取為300 m，質(zhì)量為1.65×1011kg，磁矩大小為8.8×107A·m2)時重力異常和化極磁力異常實際橫向分辨能力(圖15).

圖15 重力異常、化極磁力異常橫向分辨能力對比(a) 磁鐵礦； (b) 矽卡巖.Fig.15 Comparison of lateral resolution of gravity anomaly and reduction to the pole (RTP) of magnetic anomaly(a) Magnetite； (b) Skarn.

通過研究認為：在6000 m以淺，對于磁鐵礦和矽卡巖，化極磁力異常實際橫向分辨能力優(yōu)于重力異常.

在現(xiàn)有的重力張量觀測精度(重力張量觀測精度取為±10E)和磁力張量觀測精度(磁力張量觀測精度取為±0.04 nT/m)以及垂向識別基礎(chǔ)上，對比球體賦存磁鐵礦(剩余密度取為1.5×103kg·m-3，磁化強度取為66.0A·m-1，半徑取為300 m)和賦存矽卡巖(剩余密度取為0.24×103kg·m-3，磁化強度取為0.8A·m-1，半徑取為300 m)時重力張量Wzz、垂直磁化磁力張量Uzz的實際橫向分辨能力(圖16).

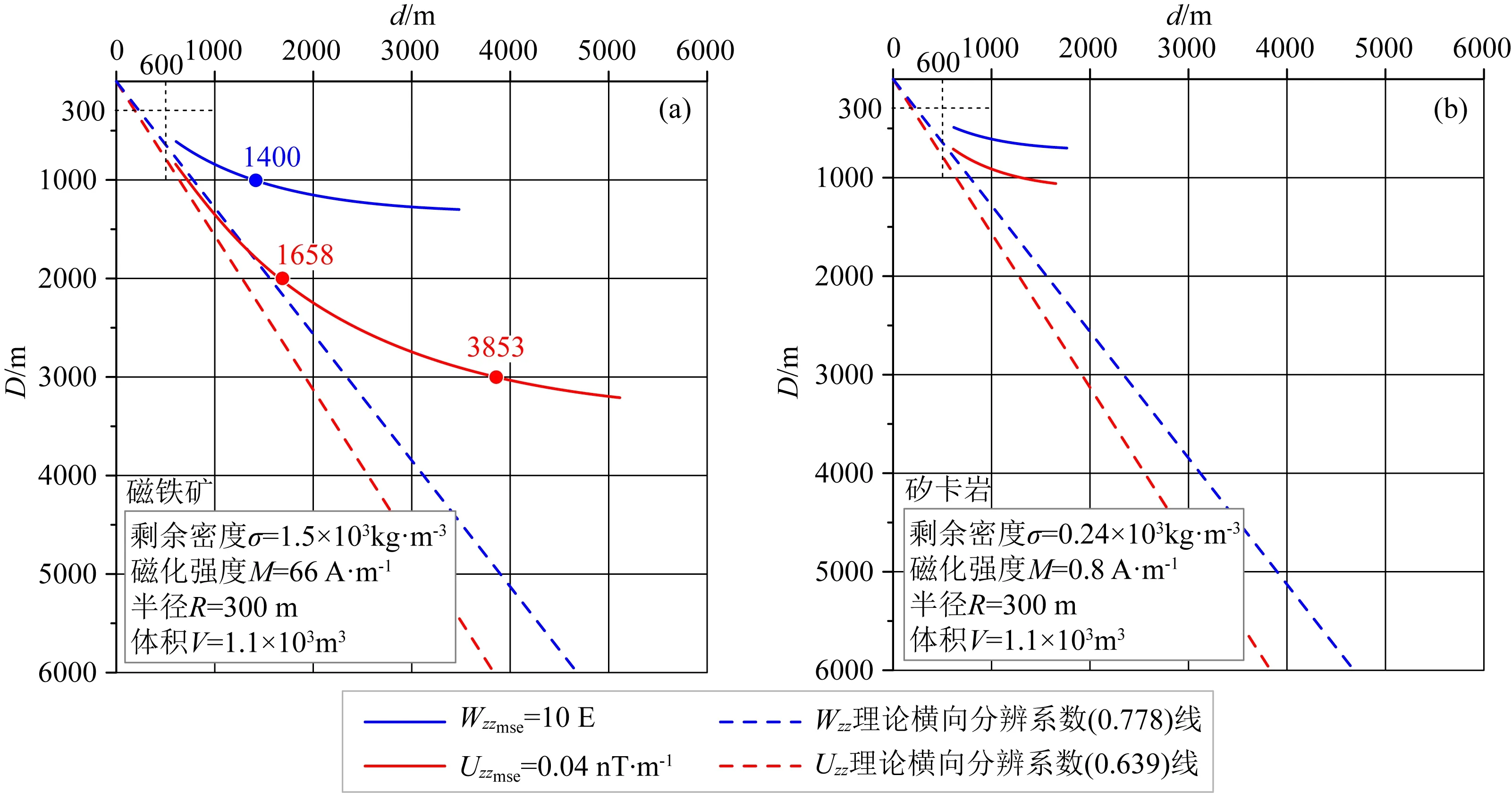
圖16 重力張量Wzz、垂直磁化磁力張量Uzz橫向分辨能力對比(a) 磁鐵礦； (b) 矽卡巖.Fig.16 Comparison of lateral resolution of gravity tensor Wzz and perpendicular magnetization magnetic tensor Uzz(a) Magnetite； (b) Skarn.

通過研究認為：在重力張量觀測精度(±10E)和磁力張量觀測精度(±0.04 nT/m)下，對于磁鐵礦和矽卡巖，垂直磁化磁力張量Uzz的實際橫向分辨能力優(yōu)于重力張量Wzz.

3.2 重力、磁力及其張量對無限延伸水平圓柱體模型橫向分辨能力研究

通過以上理論研究總結(jié)(表9)得到：重力異常、重力張量、化極磁力異常以及垂直磁化磁力張量對無限延伸水平圓柱體(線源模型)的理論橫向分辨能力由強到弱依次為：Uzz>Uxz=RTP=Wzz>Wxz>Δg.

表9 重力異常、重力張量、化極磁力異常以及垂直磁化磁力張量的理論橫向分辨系數(shù)(無限延伸水平圓柱體模型)

4 結(jié)論與建議

(1)在理想觀測精度(觀測誤差為0)下，重力異常及重力張量對球體和無限延伸水平圓柱體的理論橫向分辨系數(shù)隨深度呈線性變化.重力異常及重力張量對等質(zhì)量球體(點源模型)理論橫向分辨能力由強到弱依次為：Wxx>Wzz>Wxz=Wxy=Δg；對相同無限延伸水平圓柱體(線源模型)理論橫向分辨能力由強到弱依次為：Wzz>Wxz>Δg.在給定觀測精度下，重力異常及重力張量的實際橫向分辨能力與形體質(zhì)量以及觀測精度成正相關(guān)，實際橫向分辨能力隨深度呈指數(shù)衰減變化.

(2)在理想觀測精度(觀測誤差為0)下，化極磁力異常及垂直磁化磁力張量對球體和無限延伸水平圓柱體的理論橫向分辨能力隨深度呈線性變化.化極磁力異常及垂直磁化磁力張量對等質(zhì)量球體(點源模型)理論橫向分辨能力由強到弱依次為：Uxx>Uzz>Uxz=RTP>Uxy；對相同無限延伸水平圓柱體(點源模型)理論橫向分辨能力由強到弱依次為：Uzz>Uxz=RTP.在給定觀測精度下，化極磁力異常及垂直磁化磁力張量的實際橫向分辨能力與磁矩大小以及觀測精度成正相關(guān)，實際橫向分辨能力隨深度呈指數(shù)衰減變化.

(3)重力(重力異常、重力張量)和磁力(磁力異常、磁力張量)對等質(zhì)量球體(點源模型)理論橫向分辨能力由強到弱依次為：Uxx>Uzz>Uxz=RTP>Uxy>Wxx>Wzz>Wxz=Wxy=Δg，對相同的無限延伸水平圓柱體(線源模型)的理論橫向分辨能力由強到弱依次為：Uzz>Uxz=RTP=Wzz>Wxz>Δg.本文在給定觀測精度下(重力觀測精度取為±0.4 mGal和±0.1 mGal、磁力觀測精度取為±4.0 nT和±2.0 nT、重力張量觀測精度取為±10E、磁力張量觀測精度取為±0.04 nT/m)，對比了重力異常和化極磁力異常，重力張量Wzz和垂直磁化磁力張量Uzz對球體賦存磁鐵礦(質(zhì)量為1.65×1011kg，磁矩大小為7.26×109A·m2)和矽卡巖(質(zhì)量為1.65×1011kg，磁矩大小為8.8×107A·m2)時的實際橫向分辨能力.研究結(jié)果表明，在6000 m以淺，對于磁鐵礦和矽卡巖，化極磁力異常橫向分辨能力優(yōu)于重力異常，垂直磁化磁力張量Uzz橫向分辨能力優(yōu)于重力張量Wzz.

致謝在本文撰寫過程中，評審專家和編輯部等提出了寶貴的意見，在此謹表謝意！限于水平和篇幅，本文疏漏和不對之處，敬請批評指正.

附錄A 重力異常Δg對球體模型理論橫向分辨能力公式推導

圖1所示球體模型在剖面(x,0,0)上引起的重力異常Δg(x,0,0)表達式為

Δg(x,0,0)=

(A1)

(x+d/2)·[(x-d/2)2+D2]5/2+(x-d/2)·[(x+d/2)2+D2]5/2=0,

(A2)

對方程(A2)進行平方、移項、化簡得

x2·[(x-d/2)2+D2]5-x2·[(x+d/2)2+D2]5+2x(d/2)·[(x-d/2)2+D2]5+2x(d/2)

·[(x+d/2)2+D2]5+(d/2)2·[(x-d/2)2+D2]5-(d/2)2·[(x+d/2)2+D2]5=0，

(A3)

對方程(A3)進一步化簡得

(A4)

將方程(A4)寫為

x·f(x,d,D)=0,

(A5)

其中

f(x,d,D)=x{[(x-d/2)2+D2]5-[(x+d/2)2+D2]5}+d{[(x-d/2)2+D2]5+[(x+d/2)2+D2]5}

+[(x-d/2)2+D2]2[(x+d/2)2+D2]2+[(x-d/2)2+D2][(x+d/2)2+D2]3

+[(x+d/2)2+D2]4}.

(A6)

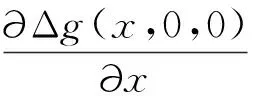
若重力異常恰能分辨兩個球體時，f(x,d,D)=0的解為x=0，將此條件代入(A6)，經(jīng)化簡得

d2-D2=0.

(A7)

附錄B 重力異常垂直張量Wzz對球體模型理論橫向分辨能力公式推導

圖1所示球體模型在剖面(x,0,0)上引起的重力垂直張量Wzz(x,0,0)表達式為

(B1)

[(x+d/2)3-4D2(x+d/2)]·[(x-d/2)2+D2]7/2+[(x-d/2)3-4D2(x-d/2)]·[(x+d/2)2+D2]7/2=0,

(B2)

對方程(B2)進行平方、移項、化簡得

{(x+d/2)6·[(x-d/2)2+D2]7-(x-d/2)6·[(x+d/2)2+D2]7}

+(-8D2){(x+d/2)4·[(x-d/2)2+D2]7-(x-d/2)4·[(x+d/2)2+D2]7}

+16D4{(x+d/2)2·[(x-d/2)2+D2]7-(x-d/2)2·[(x+d/2)2+D2]7}=0,

(B3)

對方程(B3)進一步化簡得

(B4)

其中

將方程(B4)寫為

x·f(x,d,D)=0,

(B5)

其中

(B6)

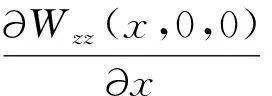
若重力垂直張量Wzz恰能分辨兩個球體時，f(x,d,D)=0的解為x=0，將此條件代入(B6)式，經(jīng)化簡可得

d7-43d5D2+448d3D4-256dD6=0.

(B7)