基于遺傳算法的可燃毒物設計優化方法研究

肖 鵬，王 健，劉仕倡,*，李滿倉，周冰燕，王連杰，陳義學

(1.中國核動力研究設計院 核反應堆系統設計技術重點實驗室，四川 成都 610213； 2.華北電力大學 核科學與工程學院，北京 102206)

核反應堆燃料組件設計是提高反應堆燃料利用率、堆芯功率展平及反應性控制的關鍵。其中，可燃毒物用于降低初始堆芯剩余反應性和冷卻劑的硼濃度，保證反應堆具有負的慢化劑溫度系數。可燃毒物組件與控制棒組件不同，為堆芯不動部件。可燃毒物組件是按物理設計分散布置于堆芯適當位置的燃料組件中，有利于展平堆芯中子注量率的分布，可提高功率密度[1-2]。通過可燃毒物材料、含量、毒物棒數量等參數，在滿足燃料和冷卻劑等反應性系數在壽期內為負、功率峰因子低于限值等約束條件下，實現降低初始反應性、反應性變化較平緩、堆芯壽期盡量長、毒物在壽期內消耗速率平緩、壽期末毒物殘留少、反應性懲罰較小等優化目標[3]。對于核反應堆燃料優化設計，由于是燃料棒、燃料組件、堆芯的多尺度問題，同時包含燃料棒、毒物棒、控制棒等多個對象，而且涉及到不同溫度、密度等各種工況，甚至還是隨堆芯燃耗深度不斷變化的動態問題，因此核反應堆燃料優化設計具有很大的挑戰性。

目前，常規的反應堆燃料設計過程通常是設計者根據經驗給出一個初步方案，再針對此方案進行堆芯物理計算分析以驗證其設計的性能，如不滿足設計目標，則調整設計參數給出新方案并再次進行計算，如此反復[4-5]。該方法能否得到優化方案，很大程度上取決于設計者的經驗，對于設計經驗缺乏人員往往耗時巨大且很難得到滿意解，即使是經驗豐富的設計者，進行優化迭代設計也非常耗時耗力。

核反應堆燃料優化設計是一多輸入多目標問題。遺傳算法作為一種有效的隨機搜索算法，具有智能性、并行性、通用性等特點[6]。它在許多領域得到了應用，取得了良好的效果。本文將遺傳算法和蒙特卡羅粒子輸運方法相結合，研究遺傳算法在壓水堆燃料組件可燃毒物多目標優化設計中的理論模型和實現方法。

1 壓水堆燃料組件中的可燃毒物設計

本文研究的可燃毒物類型為可燃毒物及燃料混合在一起的整體型可燃毒物。優化對象為13×13的壓水堆組件，其中包含3種棒：燃料棒、毒物棒和中心導管。組件結構如圖1所示。

圖1 壓水堆組件結構模型 Fig.1 PWR assembly model

1.1 可燃毒物優化變量

優化變量包括：1) 毒物材料類型，包括6種氧化物，即Gd2O3、Er2O3、Sm2O3、Eu2O3、Dy2O3、HfO2(表1)；2) 毒物含量，采用的范圍是毒物質量占含可燃毒物燃料棒整體質量(毒物+UO2)的1%～20%共20種質量百分比情況；3) 排布類型(圖2)；4) 軸向分層，在三維燃耗計算中將軸向分為5層，排列方式1表示整根棒全為可燃毒物，2表示兩端各有1層Zr層，中間3層為可燃毒物，3表示兩端4層為Zr層，只有中間1層為可燃毒物(圖3)。

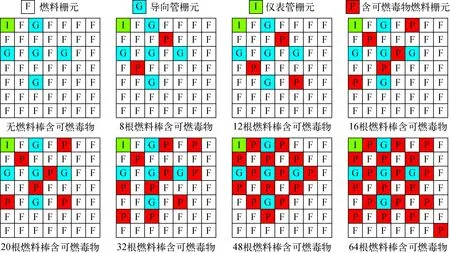
圖2 含可燃毒物燃料組件布置Fig.2 Fuel assembly layouts with burnable poison

圖3 軸向分區布置Fig.3 Axial division

表1 候選可燃毒物的密度和宏觀吸收截面Table 1 Theoretical density and macroscopic neutron absorption cross section of candidate burnable poison

1.2 可燃毒物設計目標

從中子學角度，可燃毒物設計應遵循3個原則：1) 壽期初，可燃毒物引入足夠大的負反應性；2) 壽期內，可燃毒物緩慢釋放反應性，控制功率分布，降低功率峰因子；3) 壽期末，可燃毒物的反應性懲罰盡可能小。

2 多目標優化遺傳算法

遺傳算法是一種基于自然選擇的搜索算法[7]，它通過繁殖將最適合的個體組合起來，從而找到一個多元問題的近似最優解[8]，并將潛在的新思想和變異性引入突變群體中。該算法具有很強的并行性，因此本文將遺傳算法應用于毒物選型優化這種搜索空間非常復雜的多目標優化問題[9]。

針對多目標優化問題[10]，目前采用最多的是帕累托最優解方法。帕累托前沿是以設計目標為軸的優化圖，由在圖上創建的線或平面顯示有沖突設計目標之間的優化權衡。在帕累托前沿，對于1個或多個目標，每個單獨的最優值可能較任何其他最優值都好，但不是所有的目標都是最優的。帕累托最優的成員也被稱為“非占優”[11]。

本文的多目標優化采用NSGA-Ⅲ算法。NSGA-Ⅲ隨機生成含有N個個體的初始種群，算法進行迭代直至終止條件滿足。在當前種群的基礎上，通過隨機選擇產生子代種群。為從種群中選擇最好的N個解進入下一代，首先利用基于帕累托前沿的非支配排序將其分為若干不同的非支配層。然后算法構建1個新的種群，構建方法是逐次將各非支配層的解加入到新種群中，直至新種群大小等于N，或首次大于N，丟棄第N層之后的解。對于最后一層非支配層解的選取，NSGA-Ⅱ用的是基于擁擠距離的方法，而NSGA-Ⅲ用的是基于參考點的方法。擁擠距離度量并不適合求解3個及更多目標的多目標優化問題。因此NSGA-Ⅲ采用了新的選擇機制，該機制會通過所提供的參考點，對新種群中的個體進行更加系統的分析，以選擇最后的非支配層中部分解進入新種群。因此本文選擇NSGA-Ⅲ作為多目標優化算法[12]。

同時，為提高計算效率，本文采用并行遺傳算法，將種群內的個體分配到不同的計算核心。常規遺傳算法和并行遺傳算法的基本流程示于圖4。圖4中，COREn表示第n個計算核心。不同的計算核心處理不同的單個子種群，種群間互相獨立進行進化，種群間進行個體遷移和種群競爭。因此并行遺傳算法可顯著提高計算效率。

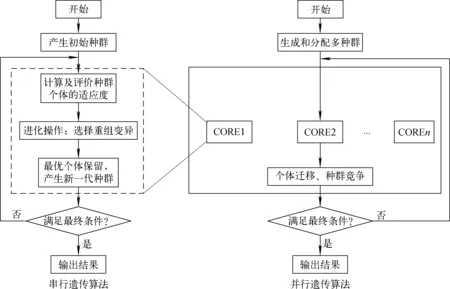
圖4 并行遺傳算法基本流程圖Fig.4 Flow chart of parallel genetic algorithm

3 可燃毒物優化數學模型

3.1 決策變量與目標函數

二維組件燃耗計算的輸入參數共3個，故定義決策變量維數為3。第1個輸入變量為可燃毒物組件的排列方式(共7種)，表示含可燃毒物燃料組件布置，具體排布見1.1節；第2個輸入變量為毒物類型，包括6種不同材料；第3個輸入變量是可燃毒物的含量，為1%～20%共20種質量占比。三維燃耗計算增加了1個決策變量，第4個決策變量是毒物棒的軸向分層，具體裝載情況見1.1節。4個變量以隨機數的形式拼接在1條染色體基因鏈上。由于各自的范圍不同，4個變量在基因鏈上的長度亦不同。因為基因鏈是由二進制編碼的，所以4個輸入變量在染色體基因鏈上的長度分別為3、3、7、2字節，基因鏈總長為15字節。

燃耗計算目標函數共5個，分別表示為F1、F2、F3、F4、F5。F1為初始有效增殖因數(keff)，F2為各燃耗步最大功率峰因子(ppf)，F3為可燃毒物在燃耗中期的含量，F4為可燃毒物在燃耗末期的含量，F5為各燃耗步中有效增殖因數的最小值(表2)。其中，毒物含量為毒物氧化物中吸收截面最大的同位素剩余百分比。總燃耗時長為1 000 d，燃耗中期含量設為第500 d的毒物含量與初始毒物含量的比值；末期含量為第1 000 d毒物含量與初始毒物含量的比值。為降低初始反應性，展平徑向功率分布，減少壽期末毒物殘留，分別設置優化目標為F1、F2和F4最小化。為使可燃毒物緩慢釋放反應性，達到最大的循環長度，分別設置優化目標為F3和F5最大化。

表2 燃耗計算決策變量和目標函數Table 2 Decision variable and objective function of burnup calculation

3.2 約束條件

組件燃耗計算中選用約束條件的方法對目標結果加以限制。在燃耗計算中，設置了4個約束條件。首先使初始有效增殖因數大于1，即F1>1。二維燃耗計算采用最大功率峰因子F2<1.4的約束條件。而在三維燃耗計算中，因三維燃耗的加入使得功率不均勻程度增大，因此設置約束條件使各燃耗步最大功率峰因子F2<3.0。此外，燃耗中期要保證一定量的可燃毒物剩余，燃耗末期剩余的可燃毒物不能過多，故增加2個約束使燃耗中期剩余毒物的含量大于1%和燃耗末期剩余毒物的含量小于10%，即F3>0.01和F4<0.1。

4 計算結果

本文的遺傳算法采用Python的Geatpy遺傳算法庫[13]。Geatpy是一個高性能實用型進化算法工具箱，提供許多已實現的進化算法中各項重要操作的庫函數，并提供高度模塊化、耦合度低的面向對象的進化算法框架，利用“定義問題類+調用算法模板”的模式進行進化優化，可用于求解單目標優化、多目標優化、復雜約束優化、組合優化、混合編碼進化優化等。組件臨界計算及燃耗計算采用清華大學REAL團隊研發的堆用蒙特卡羅程序RMC[14]，RMC具備內耦合的燃耗計算功能[15-17]。

4.1 二維組件燃耗計算

遺傳算法的種群數為50，迭代次數為50。RMC計算的源迭代采用的粒子數為2 000/代，非活躍代為5代，總代數為15，keff的統計標準差約為0.5%。比功率為30 W/gHM，燃料棒中235U的富集度為3%。不同棒數具體排列方式見1.1節。燃耗計算中采用的燃耗步數為6，步長分別為100、100、150、150、250、250 d，共1 000 d。最大平均燃耗深度為30 MW·d/kgHM。不考慮帶軸向分層，毒物棒為整根全為燃料和毒物混合的單一材料。優化方案及結果列于表3，最終的優化方案中所用的材料均為Er2O3，因此Er2O3較其他材料更優。該結果與通過人工搜索優化得到的結論一致。二維優化方案的keff隨燃耗時間的變化如圖5所示。

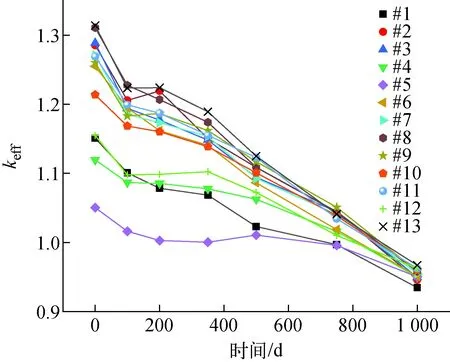
圖5 二維組件各燃耗步keff隨燃耗時間的變化Fig.5 Change of keff with burnup time of two-dimensional assembly

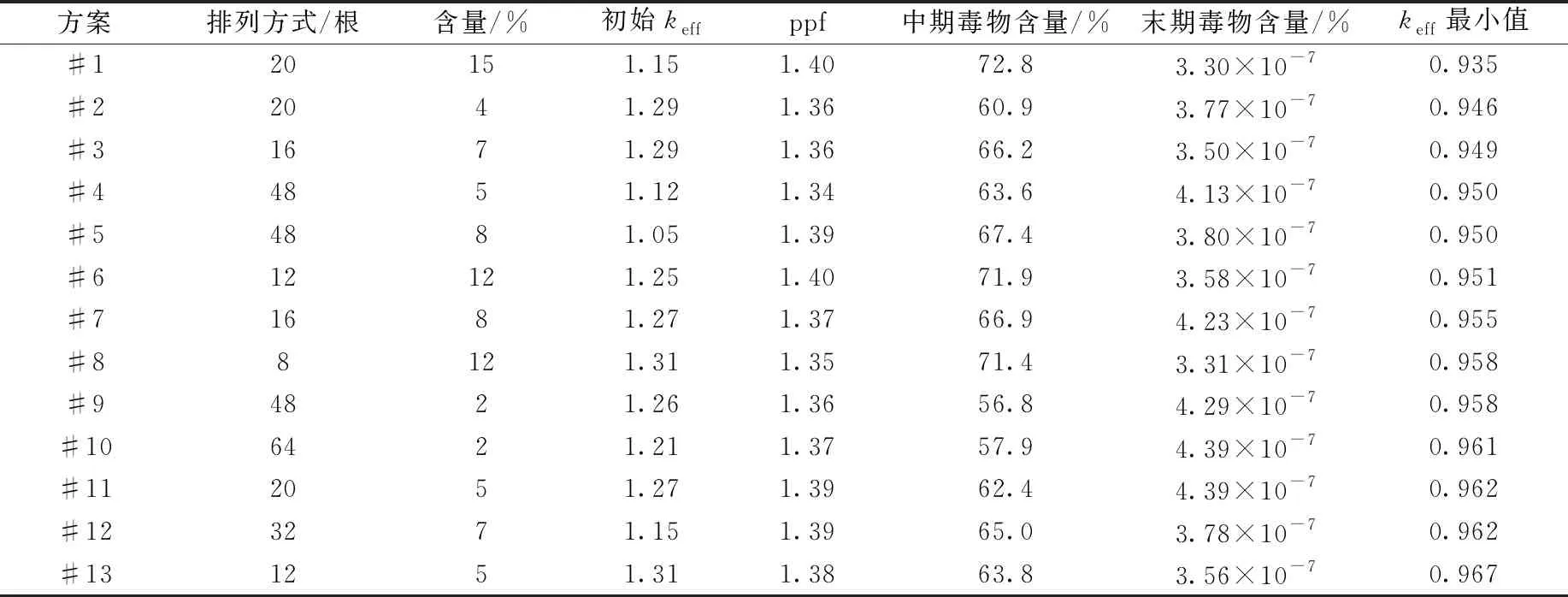
表3 二維組件燃耗計算優化方案及結果Table 3 Optimization scheme and result of two-dimensional assembly burnup calculation

4.2 三維組件燃耗計算

考慮加入軸向分層后的燃耗計算，遺傳算法的種群數和迭代次數、蒙特卡羅計算的粒子數和代數均與二維算例相同。keff的統計標準差約為0.4%。

優化后得到40個非支配解，其中Gd2O3有13個、Er2O3有21個、Sm2O3有2個、Eu2O3有4個(表4)。與二維燃耗的只有1種材料Er2O3相比，通過軸向分層使得候選材料種類增加。各材料的keff隨燃耗時間的變化如圖6所示。

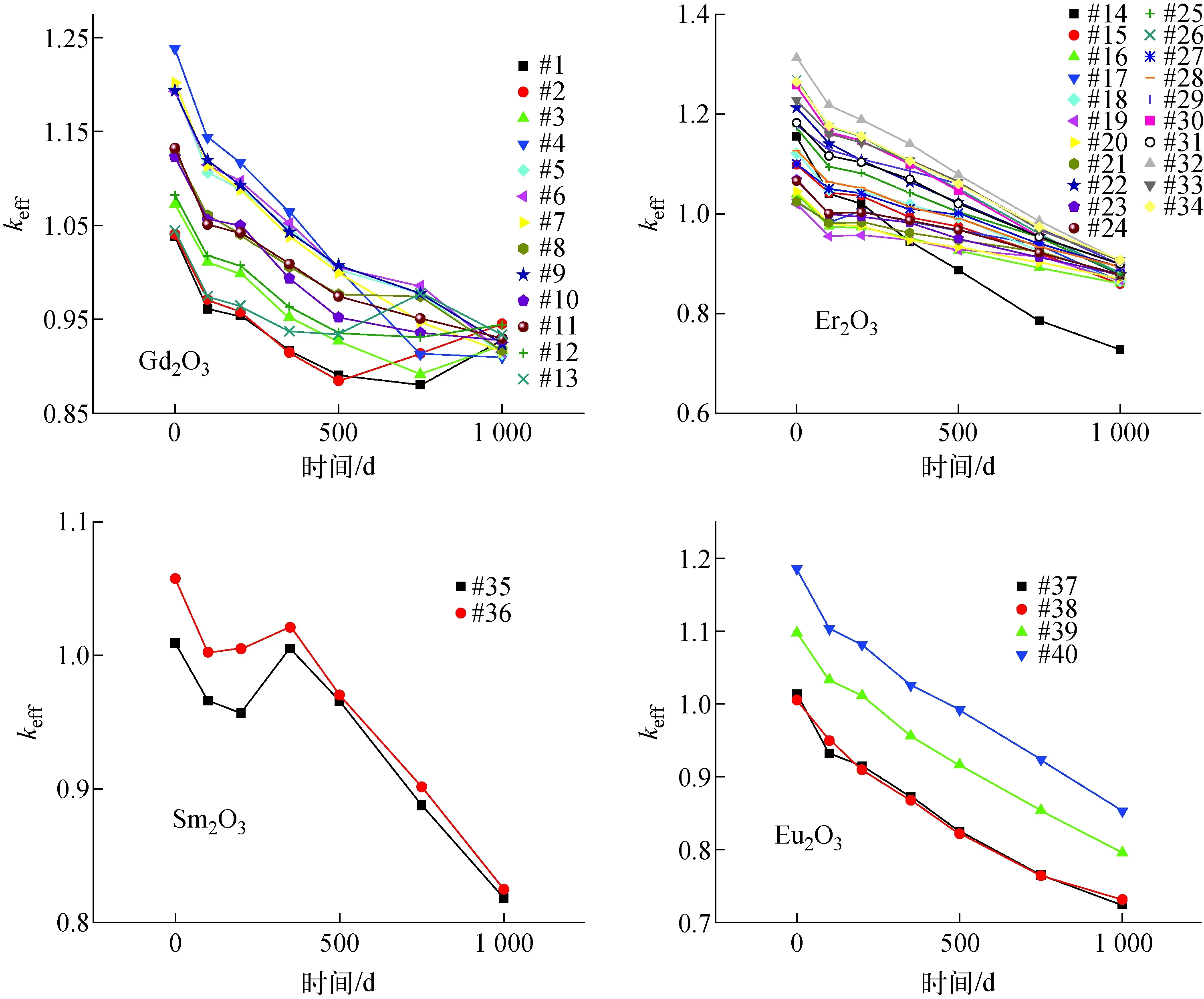
圖6 三維組件各燃耗步keff隨時間的變化Fig.6 Change of keff with burnup time of three-dimensional assembly

表4 三維組件燃耗計算優化方案及結果Table 4 Optimization scheme and result of three-dimensional assembly burnup calculation

三維燃耗ppf隨不同軸向分層的分布如圖7所示。可看出，分層方式2(即兩端各有1層Zr層、中間3層為可燃毒物)的燃耗ppf較分層方式1(即整根棒全為可燃毒物)的小。可見改變分層方式，以部分毒物代替整體全為可燃毒物的布置方式可減小ppf值。

圖7 三維燃耗ppf隨軸向分層分布的變化Fig.7 Distribution of ppf in three-dimensional burnup with axial division

5 結論

本文將多目標并行遺傳算法應用于壓水堆組件毒物選型優化，以反應性控制、功率分布和不同時期燃耗剩余等為目標，對可燃毒物材料類型、含可燃毒物燃料棒排列方式、毒物含量、軸向分層等決策變量進行了優化。針對二維和三維燃耗計算，分別篩選了13和40種優化方案。計算結果表明：Er2O3用作毒物的綜合效果最好；Gd2O3、Eu2O3和Sm2O3的應用需結合堆芯方案開展進一步研究；HfO2和Dy2O3不適合用作可燃毒物。該結果與通過人工搜索優化得到的結論基本一致。同時，三維軸向分層可為優化提供更多可選的材料種類方案，以部分毒物的分層布置方式可減小ppf值。

通過本文計算，初步驗證了智能優化算法在進行毒物選型優化時，具有一定的協助工程師進行優化設計方案篩選的潛力。