簡化反應堆一回路系統自然循環的動態比例特性研究

李向賓，詹奔騰，王忠毅，李浩永

(1.華北電力大學，北京 102206；2.非能動核能安全技術北京市重點實驗室，北京 102206；3.國家電投集團科學技術研究院有限公司，北京 102209)

自然循環作為關鍵非能動技術之一，已廣泛應用于先進反應堆的非能動系統。如事故工況時非能動堆芯冷卻系統可通過自然循環及時排出堆芯余熱，從而保證反應堆的安全。通常情況下，對應的自然循環均處于瞬態過程。鑒于瞬態過程的復雜性，有必要通過試驗深入了解其動態特性。限于規模和經濟性，大部分試驗均是基于縮比試驗臺架進行的，故必須進行比例分析來保證模型試驗對原型現象的可復現性[1]。如AP600/AP1000/CAP1400系列核電站非能動系統的性能驗證即基于APEX、SPES、ROSA和ACME等4個縮比實驗臺架的實驗結果而定[2-5]。而數十年來，關于自然循環的比例分析方法也得到了較充分的發展。Ishii等[6]研究得到了基于一維守恒方程的單相和兩相自然循環的比例準則；趙冬建等[7-8]在一維漂移流模型的基礎上導出了兩相自然循環相似準則；盧冬華等[9-10]分析得到了1組統一的適用于單相和兩相自然循環系統的無量綱準則數組。這些方法作為經典H2TS(雙向分層比例分析)方法的進一步發展[11]，已被應用于相關自然循環系統的縮比設計。但以前的研究并沒有基于上述方法對自然循環瞬態過程關鍵參數的變化特性進行評價。Reyes[12]提出了一種動態比例分析(DSS)理論，將守恒方程的積分形式變換為相空間坐標內的形式，并通過二參數的仿射變換得到對應的比例縮放方法，以此來研究動態的比例進程。文獻[13]將此理論發展應用于簡單矩形環路內單相自然循環瞬態進程的比例分析，但并沒有應用于反應堆系統。

本文基于簡化反應堆一回路系統，在實驗驗證的基礎上，利用H2TS和DSS方法對其自然循環現象進行比例分析，同時使用RELAP5程序計算不同比例尺度下升降功率時的自然循環瞬態過程[14]，并將兩種方法下的計算結果進行對比分析，評估對應工況下關鍵參數的動態變化規律。

1 比例分析

之前的研究已詳細給出了簡單矩形環路內單相自然循環的相似準則數[13]。為簡化起見，本文僅列出相關的修改部分。首先，基于H2TS方法下的自然循環相似準則數為：

(1)

(2)

(3)

其中：∏Ri為表征浮力和慣性力之比的理查森數；β為流體熱膨脹系數；g為重力加速度；H為冷熱段中心位置高度差；ΔT0為冷熱段穩態溫差；u0為穩態流動速度；∏Fri為摩擦數；f為摩擦系數；l為循環通道長度；d為管道直徑；k為局部損失系數；∏Qs為熱源數；q為加熱段熱流密度；ρ為流體密度；cp為流體比定壓熱容。為保證模型和原型現象相似，對應的相似準則數應相等，即模型和原型準則數的比值∏R=∏m/∏p=1。一般情況下，摩擦數可通過調整環路內的阻力系數而得到滿足，故可暫不考慮。考慮到堆芯實際結構參數，上述熱源數可修訂為：

(4)

其中：ζ0為加熱周長；ai,0為截面積。

設模型和原型的堆芯組件結構相同，即管徑和柵距保持不變[9]，則有：

a0,R=ζ0,R

(5)

在等物性條件下，由式(1)和(5)可得H2TS方法下對應的相似準則，即：

(6)

本研究中，在縮比實驗臺架的堆芯模擬體內，應用1個燃料組件模擬體作為熱源，對應原型電廠157個燃料組件，由式(5)可得管道的直徑比dR=0.138 3。則等物性條件下的相似準則可歸納為：

(7)

文獻[13]中已詳細推導了簡單矩形環路內基于DSS方法下的單相自然循環相似準則。為便于同H2TS進行對比，仍設定不對摩擦數進行相似分析(僅由系統調整保證)，且取dR=0.138 3，則等物性條件下基于DSS方法所得的相似準則為：

dR=0.138 3，u0,R=lR，qR=lR

(8)

對比兩種方法下的相似準則可知，若取同樣的縮比尺寸，則采用兩種方法所得的縮比模型幾何結構完全相同，而速度比和熱流密度比則明顯不同。顯然，采用DSS方法所需的模型熱流密度明顯小于基于H2TS方法所得的對應數值，這與文獻[13]結論一致，也是DSS方法的一個明顯特點。

2 數值模型驗證

為保證計算的準確性，首先將已有的實驗結果與基于RELAP5程序計算所得的結果進行對比。

2.1 模型

圖1為用于測試反應堆一回路系統自然循環現象的全壓自然循環實驗臺架(FITY)簡化示意圖[15]。此臺架是以壓水堆為原型、H2TS方法為理論指導得到的實驗裝置(長度比例為1∶4)，主要包括1個堆芯模擬體(含有1個與原型反應堆系統完全相同的燃料組件)、1個蒸汽發生器、1個穩壓器及相關管路和閥門。實驗時，堆芯模擬體和蒸汽發生器分別作為熱源和冷源，即可形成自然循環。為利用RELAP5程序進行計算，首先基于此實驗臺架建模并進行組件劃分，節點示意圖如圖2所示。其中，108管道組件代表作為熱源的堆芯模擬體，116和204管道組件分別代表蒸汽發生器傳熱管的管側和殼側，環路壓力通過波動管304由穩壓器302控制，泵組件121在自然循環期間僅提供阻力。內置于二次側水箱中的216和217管道組件作為二次側傳熱管，用于排出系統熱量。計算所采用的邊界條件和初始條件均依據實驗數據設置。

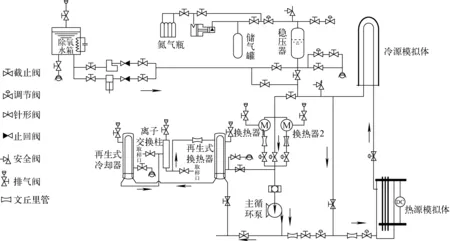
圖1 自然循環實驗臺架示意圖Fig.1 Natural circulation test facility scheme

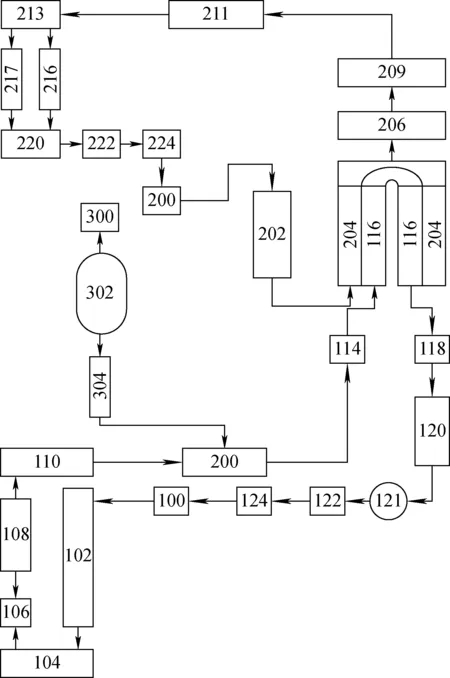
圖2 數值模型節點示意圖Fig.2 FITY nodalization scheme

2.2 驗證

1) 節點敏感性分析

為評估不同節點數對計算結果的影響，以加熱段108組件為例，分別計算不同節點數時其出口的穩態溫度，如圖3所示。可看出，108組件的溫度變化范圍隨節點數的增加而減小，且當節點數到達8以上后，其趨勢已明顯變緩。因此，綜合考慮計算時間和計算精度，加熱段的節點數選為11，其他各組件的節點數也做類似處理。

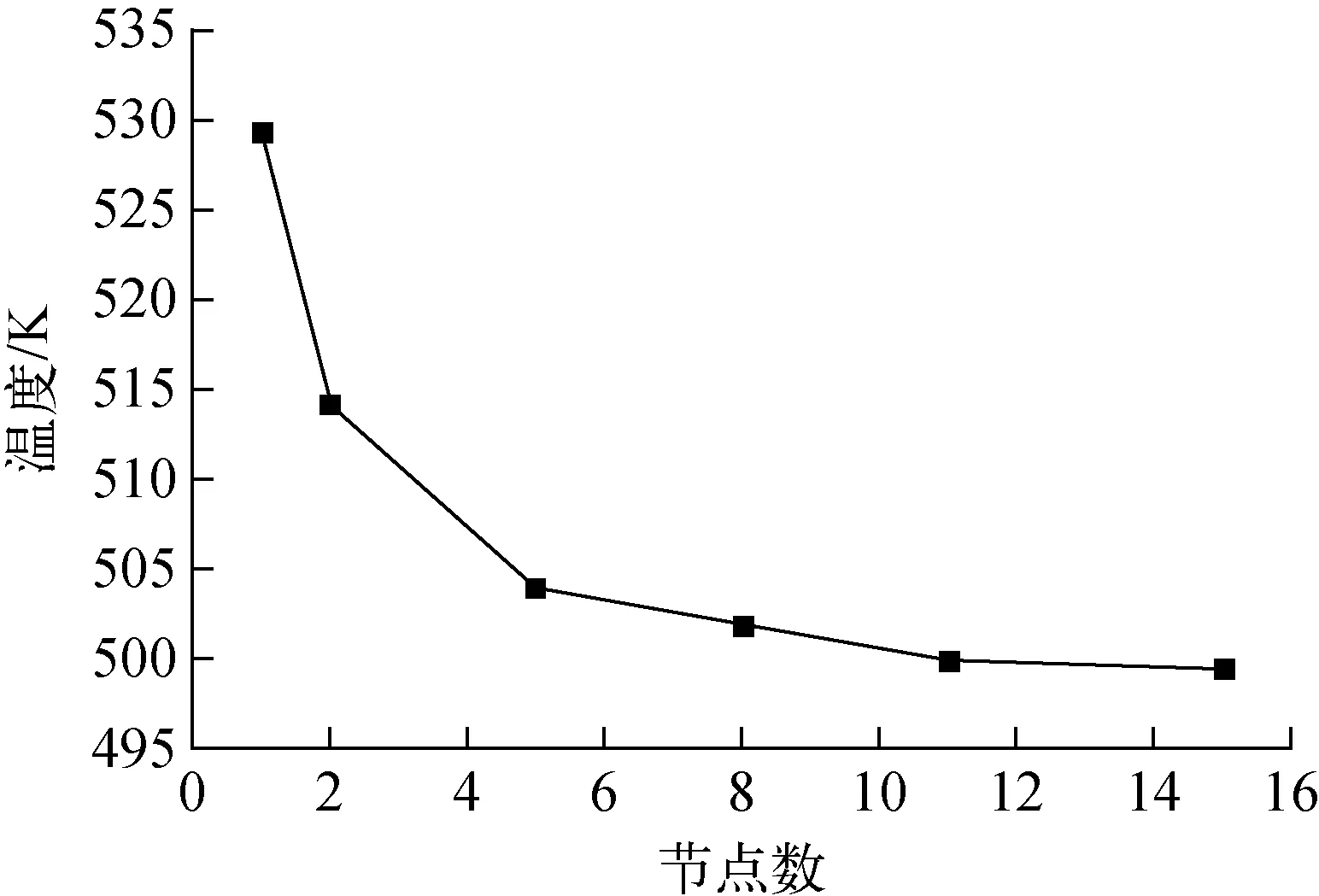
圖3 108段出口溫度隨節點數的變化Fig.3 Temperature at 108 exit under different node numbers

2) 穩態結果分析

首先，分別采用實驗和數值計算獲得5種不同加熱功率(136、149.5、167.9、183.2、218.0 kW)下環路內的穩態自然循環流量，結果如圖4所示。其中，EXP和RELAP分別代表實驗結果和數值計算結果。可見，環路流量均隨加熱功率而增大，數值計算結果與實驗結果基本一致，兩者間的最大誤差約為3%。在單相自然循環情況下，其他工作壓力下的流量對比結果以及冷熱段溫差計算結果的偏差均與此類似，說明數值計算結果可較好地反映實驗現象。

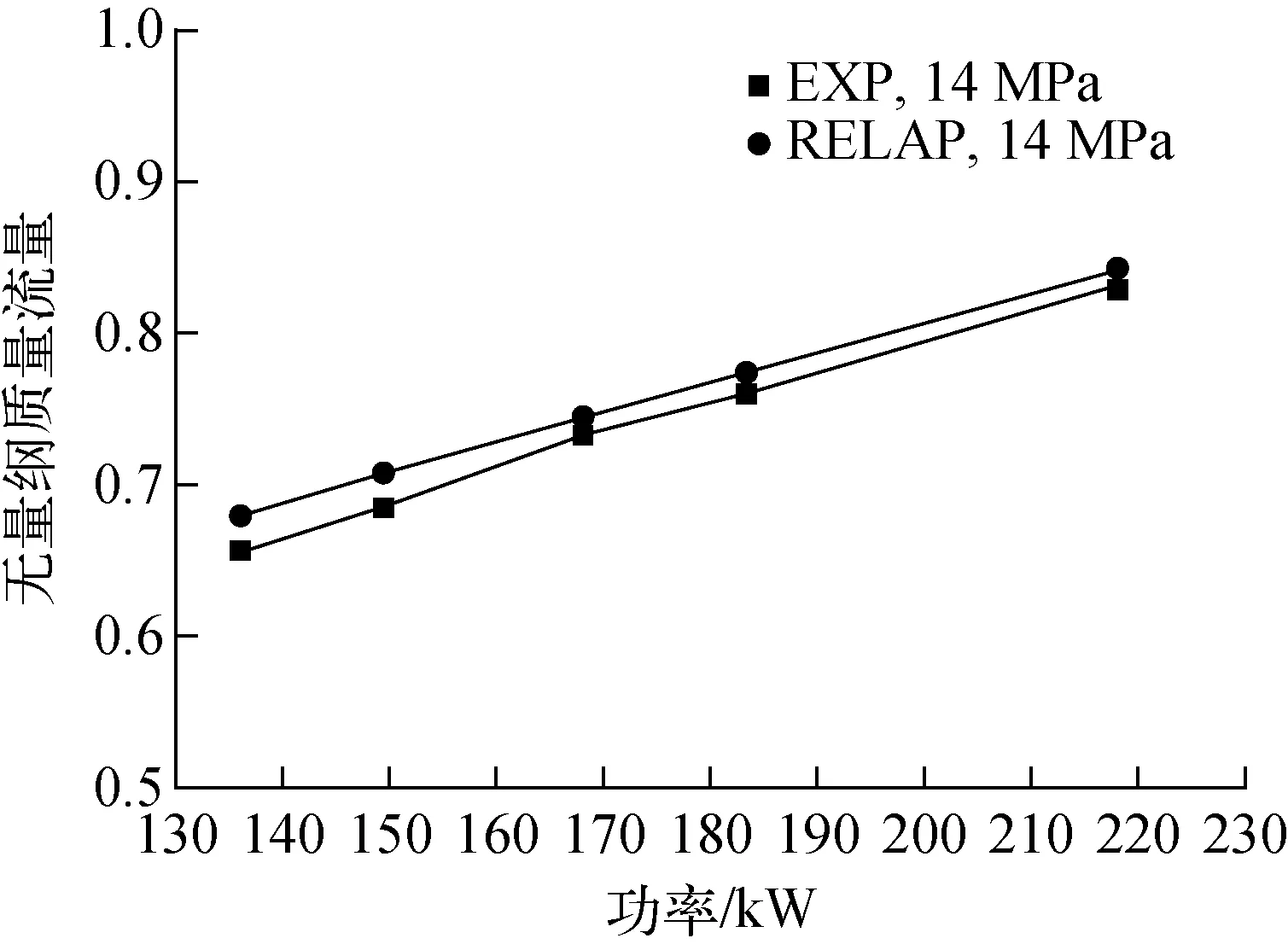
圖4 無量綱質量流量隨加熱功率的變化Fig.4 Dimensionless mass flow rate under different heating powers

3) 瞬態結果分析

表1列出了包括4種階躍升功率工況和3種階躍降功率工況下的功率設置。對于每一種工況，首先在初始功率下達到穩態，之后再按照設定的功率變化速度進行功率調整，直至達到最終設定功率，并趨于穩態。本文中，選擇不同的功率變化速度是為了評估功率變化速度對環路自然循環的影響。功率階躍變化的最大值約為初始功率的5%。

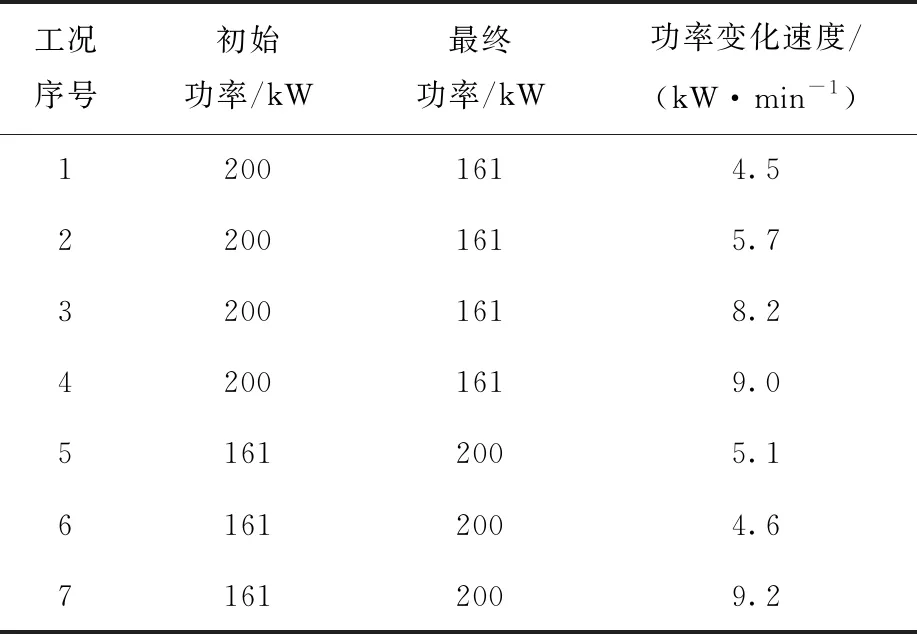
表1 瞬態工況下的功率設置Table 1 Power setting under transient condition

圖5為降功率和升功率情況下的瞬態質量流量分布。其中，EXP-x和RELAP-x分別代表x工況下的實驗結果和數值計算結果。

由圖5a可看出，在所有工況下，流量的變化速度都直接受到加熱功率變化速度的影響。功率下降得越快，流量到達穩定所需的時間越短，但流量波動幅度越大。相對于功率以初始值3%左右的速度階躍下降的工況(對應工況1和2)，功率以初始值5%左右速度階躍下降時(對應工況3和4)的流量變化快得多。500 s之前，實驗值的波動幅度明顯高于計算值。這是因為數值計算僅基于沿流動方向的一維流動而獲得，而且所采用的時間步長可更小，因此質量流量變化相對平穩，而實際實驗測量則受采集頻率等多種因素的影響，故波動幅度較大。穩態時實驗值和計算值的總體偏差約為7%，且計算值的下降幅度更小。這是因為目前所測數據是一回路的流量，而實驗時二回路對一回路的冷卻也同樣基于一個非能動系統完成。穩態時，一回路加熱功率和二回路冷卻系統處于平衡狀態；功率下降時，二回路系統自然循環的響應相對延緩，在此過程中帶走的熱量偏多，所以平衡時一回路維持在低流量水平(同理，升功率時一回路維持在高流量水平，圖5b)。而數值模擬時對二回路系統做了部分簡化處理，導致響應加快。

從圖5b可知，各工況的實驗值和計算值的偏差及對應變化特征與降功率工況下的情況基本類似。需要指出的是，工況7下的流量峰值，包括實驗值和計算值，均明顯高于最終的穩態值。這是由于工況7下功率階躍變化速度較大(范圍約為初始值的5.7%)。因此，以下計算中的功率階躍變化范圍限制為初始功率的5%，以避免過大的流量波動。總體上，RELAP5程序可較好地模擬瞬態自然循環。

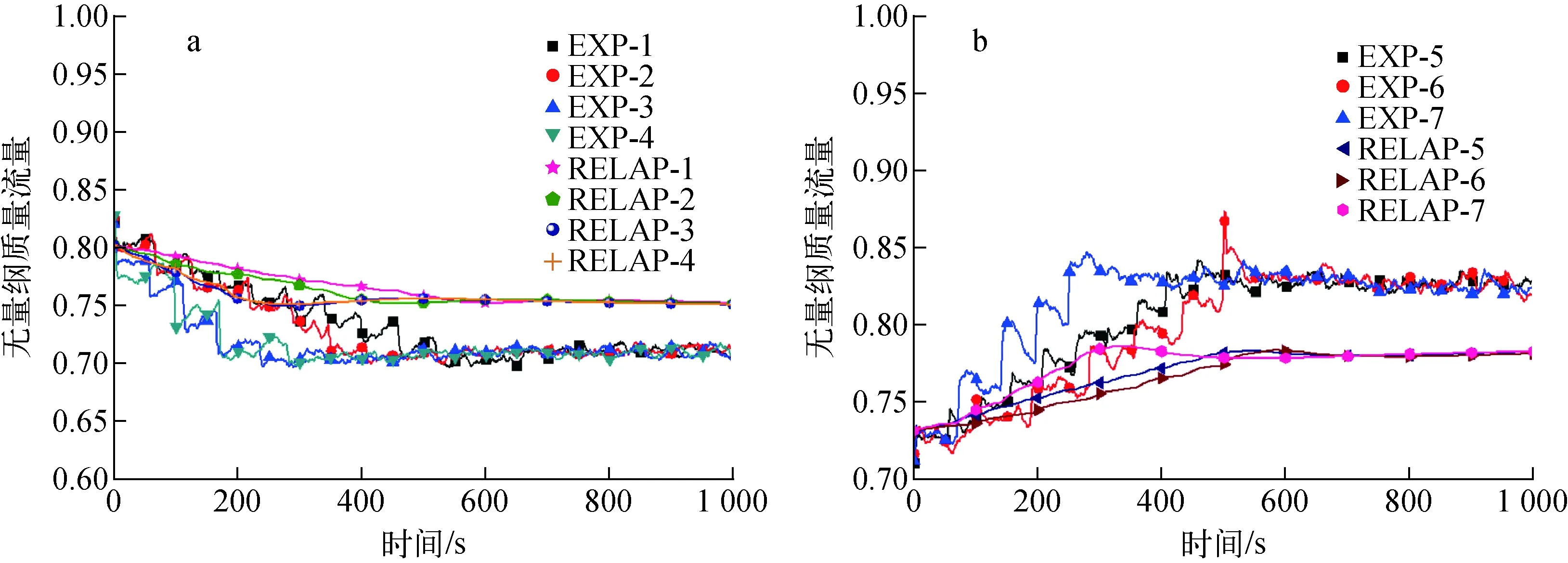
圖5 降功率(a)和升功率(b)下的瞬態質量流量Fig.5 Mass flow rate under power-down case (a) and power-up case (b)

3 比例特性分析

基于一典型的長度比例lR=0.25來分析瞬態自然循環的比例特性。表2為分別基于H2TS方法和DSS方法所得的比例數。可看到，在相同的幾何尺度下，基于DSS方法可得到更小的縮比功率。利用RELAP5程序分別計算了降功率工況和升功率工況下的自然循環，并將結果進行了對比。

表2 基于H2TS方法和DSS方法所得的比例數Table 2 Scaling number based on H2TS and DSS methods

3.1 降功率工況結果分析

本文模擬了4種降功率工況，功率變化均采用階躍下降形式，具體參數列于表3。

表3 降功率工況下的功率設置Table 3 Power setting under power-down case

圖6為所有工況下的流量變化，其中H2TS-x和DSS-x分別為基于兩種比例方法所得縮比模型不同工況下的計算結果，t*=t/t0為參考時間，t0為不同比例方法下系統功率改變后下一個穩態循環周期所需的時間。為便于對比，根據對應工況下時間比例的要求對t0進行了比例調整。可見，兩種方法下所得的質量流量變化趨勢均與原型結果類似，即流量在初始階段較短時間內迅速變大，之后在經歷一段時間的波動后，又開始逐漸增大。總體來看，基于H2TS方法計算所得的流量到達穩態值的時間稍長，而基于DSS方法計算得出的流量更接近于原型結果。另外，兩種方法下4種工況所得的流量曲線都分別重合，這說明5%階躍功率范圍內不同的功率變化速度對自然循環的瞬態流量變化沒有明顯影響。

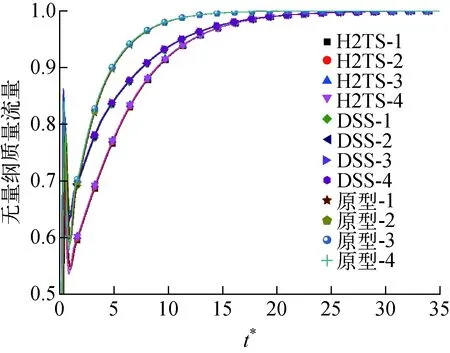
圖6 工況1～4下的瞬態質量流量對比Fig.6 Transient mass flow rate under case 1-4

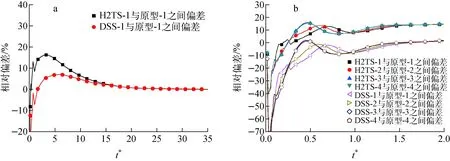
a——長循環周期；b——前兩個循環周期圖7 不同循環周期內的質量流量相對偏差Fig.7 Relative error of mass flow rate in different cycles

圖8為工況1下基于冷段和熱段出口溫度計算得到的溫差曲線及對應的相對偏差。由圖8a可看出，初始階段冷熱段溫差的波動幅度大于流量波動幅度，這是因為功率突變時首先會造成溫度的變化。對比流量變化曲線可知，基于H2TS方法所得的溫差曲線更接近于原型。由圖8b可見，溫差偏差變化趨勢與流量偏差類似，但基于DSS方法所得偏差較大。

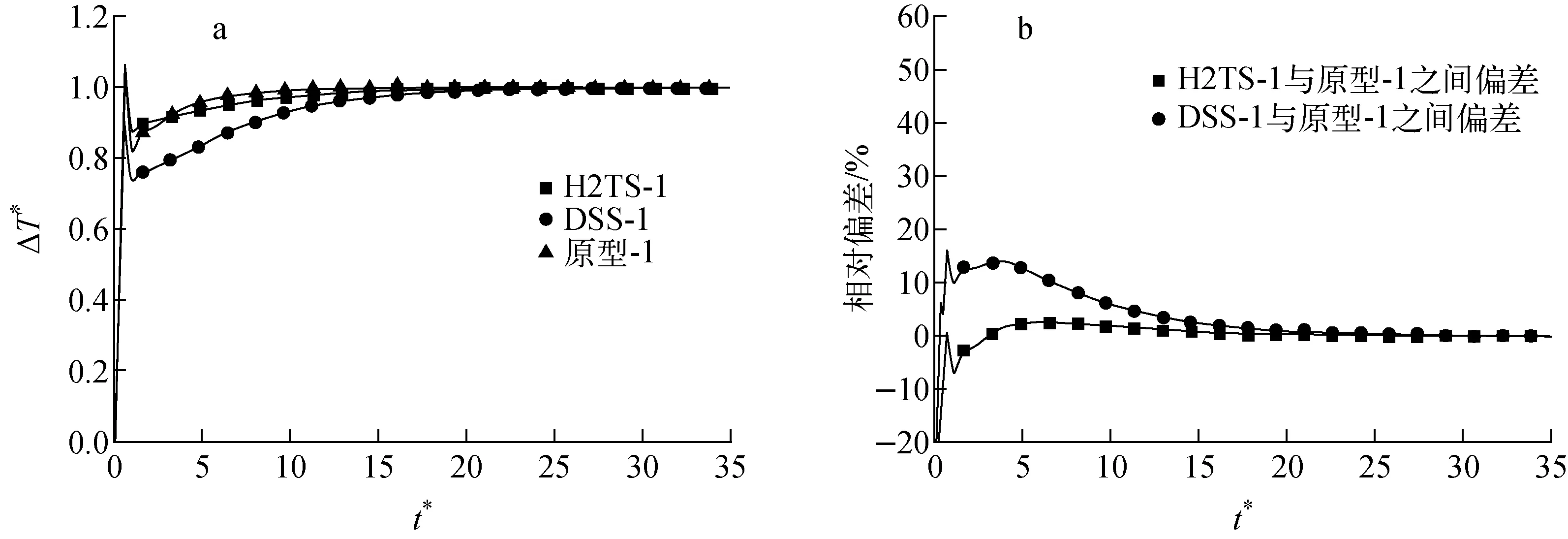
圖8 工況1下的瞬態溫差(a)及其偏差(b)分布Fig.8 Transient temperature difference (a) and its relative error (b) under case 1

3.2 升功率工況結果分析

為便于對比，計算了基于3種不同功率變化速度的升功率工況下的自然循環，功率變化仍設置為階躍形式(表4)。圖9為工況5下的流量曲線及對應的偏差曲線，其他工況下的變化與此類似。對比降功率工況可知，基于H2TS方法所得流量更接近原型工況數值，而初始階段基于DSS方法的偏差明顯大于基于H2TS方法的偏差。圖10為前兩個循環周期內所有升功率工況下的流量偏差，其總體變化趨勢與降功率工況類似。圖11為工況5下的溫差曲線，所有曲線都有較高的重合度，對應的總體偏差都非常小，均在5%范圍內。

表4 升功率工況下的功率設置Table 4 Power setting under power-up case

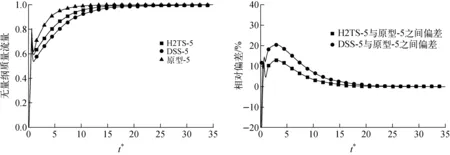
圖9 工況5下的瞬態質量流量及其偏差Fig.9 Transient mass flow rate and its relative error under case 5

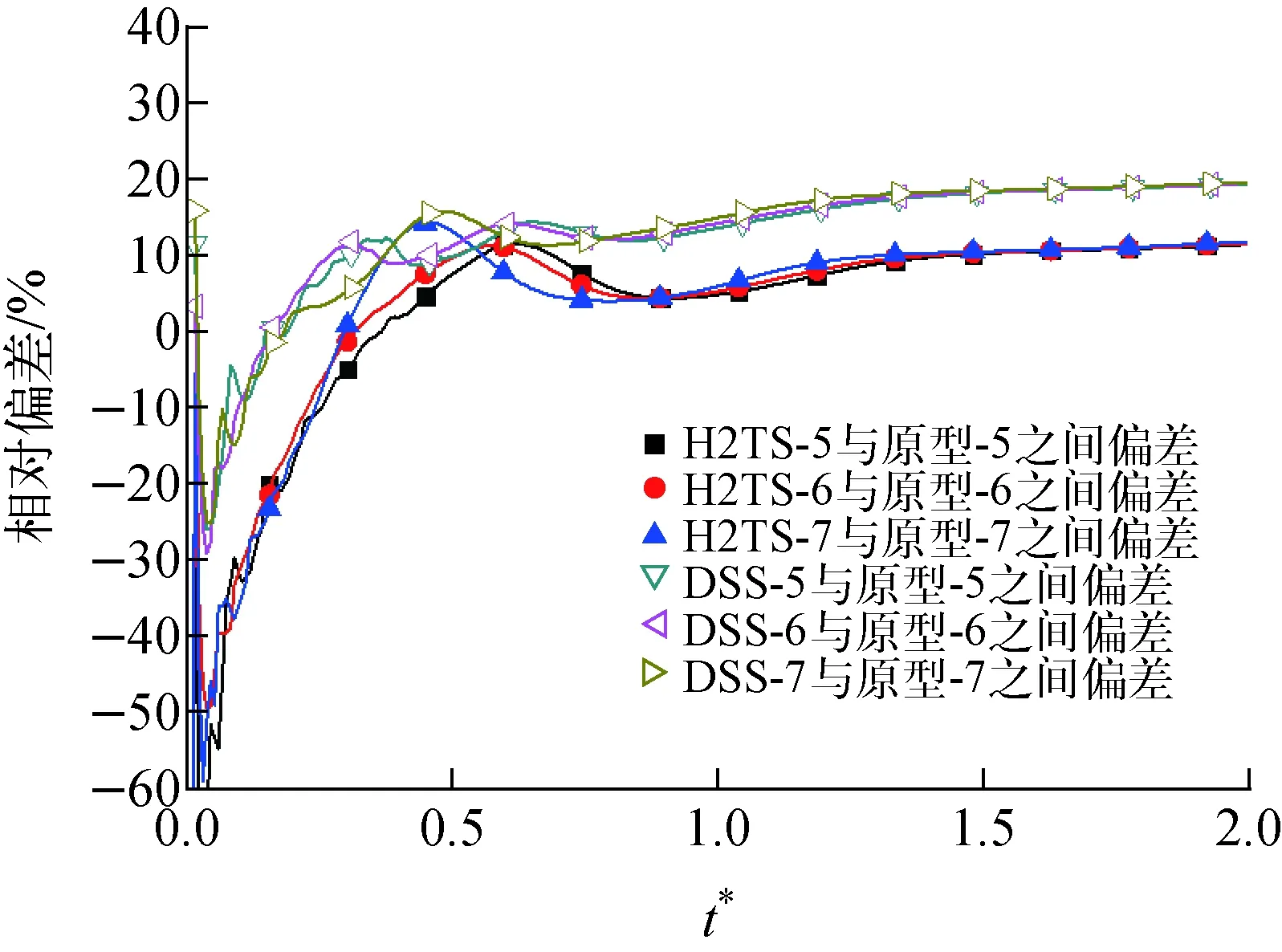
圖10 前兩個周期內的質量流量偏差Fig.10 Relative error of mass flow rate in the first two cycles

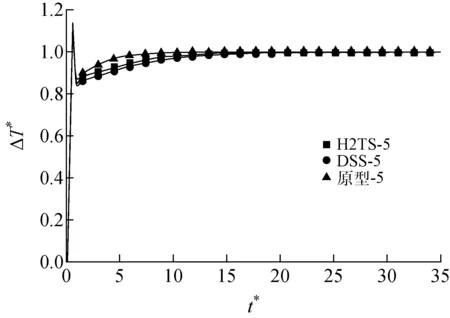
圖11 工況5下的瞬態溫差分布Fig.11 Transient temperature difference under case 5

4 結論

針對簡化反應堆一回路系統的自然循環，分別采用H2TS方法和DSS方法進行了比例分析，并在實驗驗證的基礎上，模擬了降功率工況和升功率工況下自然循環的瞬態過程，分析了自然循環流量等關鍵參數的動態變化，得到如下結論：

1) 基于RELAP5的數值計算結果與實驗結果基本一致，5%初始功率內的階躍功率變化不會引起過大的流量波動；

2) 基于兩種比例分析方法所得縮比模型下的計算結果均可反映原型參數變化，流量和溫差的整體失真度均小于20%；

3) 所有工況下，自然循環流量和溫差在初始階段0.5個循環周期內存在較大的波動，之后則相對平穩。

本文僅針對簡化反應堆一回路系統內瞬態自然循環的關鍵參數變化規律進行了對比分析。關于不同比例分析方法下相似準則數的動態失真度評價以及各類參數變化的不確定性分析，包括升降功率工況下流量失真度的不同變化特點，將在后續研究中進一步探討。