基于強度折減法的巴彥哈爾露天邊坡穩定性分析

張冬巖，苗勇剛，張長鎖

（1 內蒙古金中礦業有限公司，內蒙古 錫林郭勒 011300；2 礦冶科技集團有限公司，北京 100160）

傳統的極限平衡理論分析邊坡穩定性時沒有考慮應力應變關系，不能通過計算收斂求解安全系數，在求安全系數時需要先假定滑移面失穩模式，并且通過簡化切片方法求解安全系數，導致精度降低，與真實的安全系數偏差較大。而有限元能夠模擬巖土體受各種邊界條件下應力應變關系，有限元強度折減法經常用于模擬邊坡穩定性，并得到了許多學者的認可。Zienkiewicz 等人早在1975 年就將強度折減法應用于邊坡穩定性分析[1]。之后由Donald 和Giam[2]，Matsui 和San[3]等人在實踐中應用并不斷改進。鄭穎人[4]、唐芬[5]等人根據強度折減原理、屈服準則等方面開展了進一步的研究，提高了計算精度，擴大了在實際工程中的應用范圍[6]。

1 強度折減法分析邊坡穩定性的優點

強度折減法已被許多成熟的巖土工程有限元軟件所應用，主要的優點如下[7]：

（1）通過重力載荷的施加和剪切強度的降低而自動產生的剪切應變可以找到臨界破壞面；

（2）求解安全系數時，不用先假定邊坡破壞的形狀，也無需進行條分。

（3）它適用于具有復雜地貌、地質的邊坡進行計算，并且可以提供極限平衡分析法無法實現的信息，例如應力，運動和孔隙壓力。

2 北露天邊坡概況

巴彥哈爾金礦礦區構造處于隆起帶復式背斜西端收斂部位，構造較為簡單。斷裂帶呈北東—南西向分布，但破碎帶內已被斷層角礫巖貫入[8]。一般地表風化強烈，強風化帶60 ～80 m 左右，其下逐漸過渡為中等風化、弱風化或完整基巖，邊坡不易發生整體性滑坡，但是可能發育小型的崩塌地質災害。根據巴彥哈爾金礦北露天邊坡的工程地質特征，選取具有典型意義的能反映巴彥哈爾金礦北露天邊坡穩定性的63 線（礦體下盤）和71 線（礦體上盤）工程地質剖面作為分析剖面，選取的兩條工程地質剖面圖如圖1～2 所示。

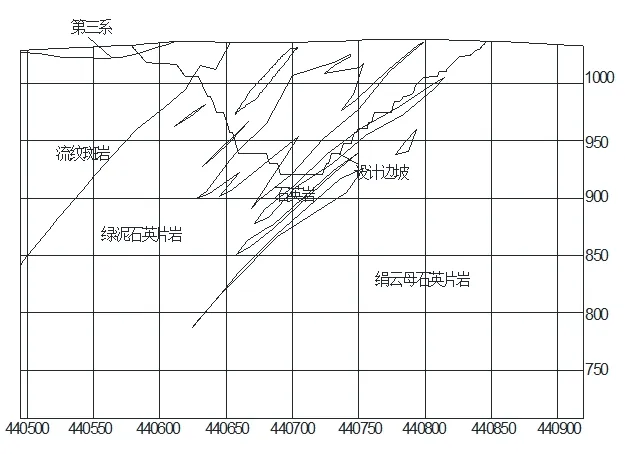
圖1 63 線工程地質剖面

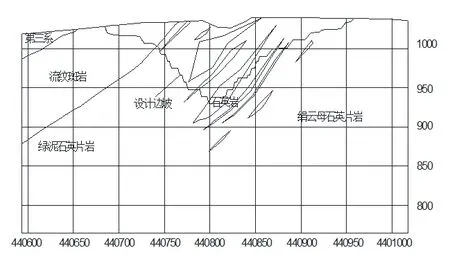
圖2 71 線工程地質剖面

3 強度折減法基本原理

強度折減系數法的基本原理是將材料的粘結力和摩擦角參數值同時除以折減系數F，得到新的值，將該值作為新的參數再進行循環計算。通過不斷折減，當結果不收斂時，所得到的值稱為邊坡最小穩定安全系數，此時邊坡達到極限平衡狀態，發生剪切破壞，同時可得到邊坡的破壞滑動面[9]。表達式如下：

式中：C′—折減后的粘聚力，KPa；φ′—折減后的摩擦角，°；F—折減系數。

4 邊坡穩定性的有限元分析

4.1 巖體力學參數

根據露天邊坡開挖后巖體的分布特點，本研究考慮了5 種巖性，即綠泥石英片巖、流紋斑巖、絹云母石英片巖、石英巖、第四系，其力學性質如表1 所示。

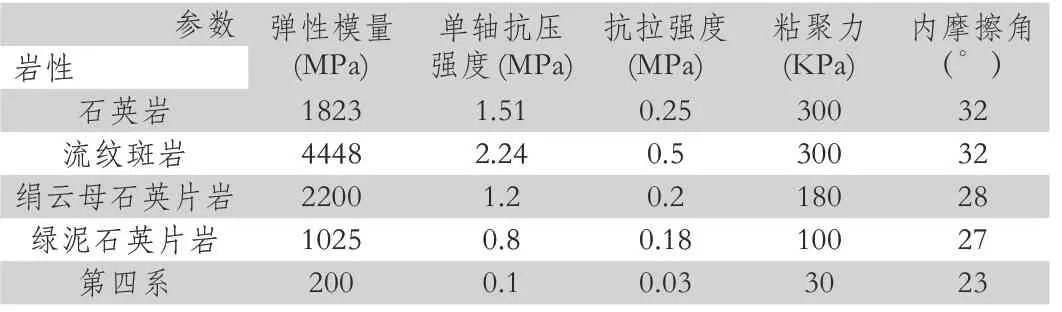
表1 露采邊坡巖體力學參數

4.2 計算模型

根據選取的63 線（礦體下盤）和71 線（礦體上盤）分析剖面，分別建立M1（坑底標高900，邊坡角為42°）、M2（坑底標高900，邊坡角為40°）兩個有限元分析模型（如圖3 ～4 所示），進行平面應變分析，主要分析邊坡在自重應力場作用下的穩定性情況。

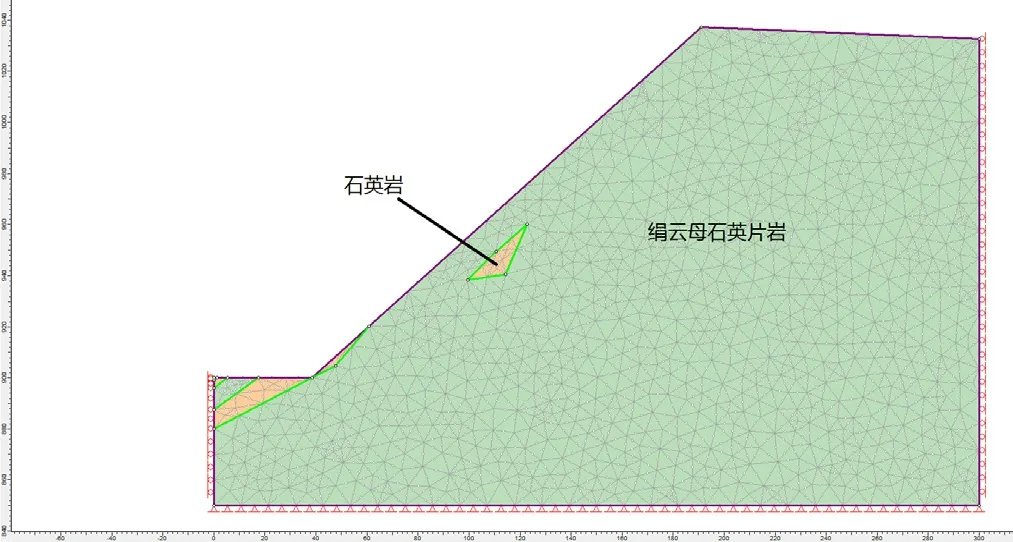
圖3 M1 模型有限元網格圖

邊界條件為：邊坡兩側水平方向固定，底部垂直方向固定，坡面為自由面，頂部為自重應力場。

根據Mohr-Coulumb 屈服準則和最大拉應力判據來確定邊坡開挖后可能出現的應力、位移、拉剪破壞范圍等，以此來分析巴彥哈爾金礦北露天邊坡的穩定性狀況。

數值模擬采用加拿大巖土工程分析軟件Phase2 8.0，主要應用于地下或地表邊坡工程開挖中的應力和位移分析，可用于分析模擬地下硐室開挖與支護、邊坡開挖等問題。在進行分析時的載荷按程序自動分級施加，解方程時用Gaussian 消除法求解，最大重復次數為500 次，累計誤差為0.001[10,11]。

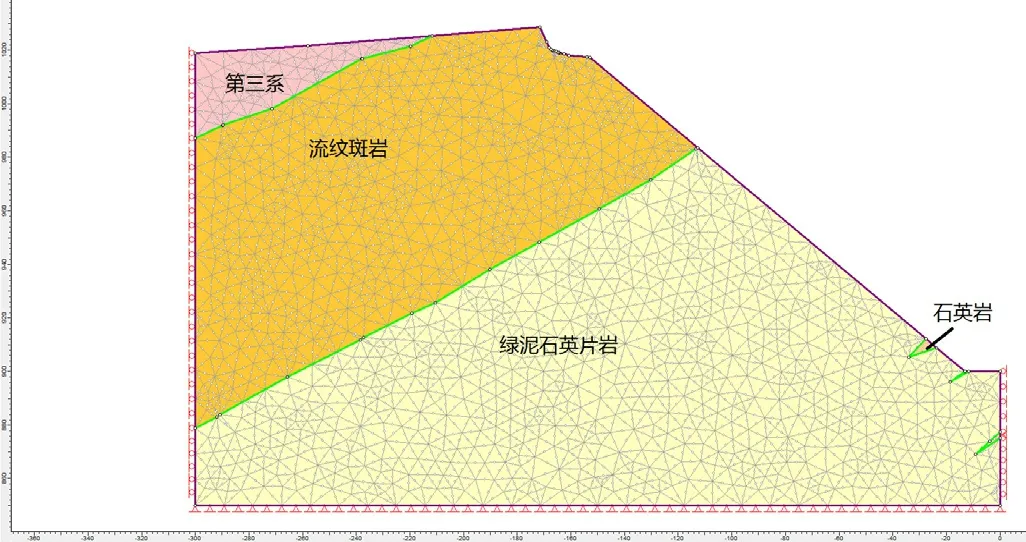
圖4 M2 模型有限元網格圖

5 計算結果及分析

5.1 M1 模型分析結果

（1）應力分析

通過對M1 模型的最大應力等值線分布圖（如圖5 所示）可以看出：最大應力值隨埋深的增加而增大，接近邊坡坡面時最大主應力值變小且呈順坡方向變化，在坡體的下部受開采擾動的影響，應力變化較大，坡面及坡面附近存在一定的拉應力，最大值的為0.2MPa。

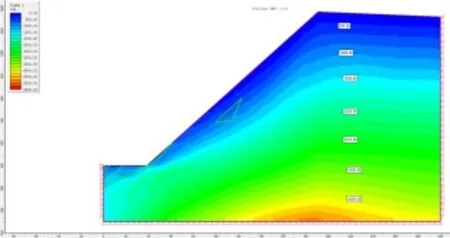
圖5 M1 模型的最大主應力等值線（σ1）分布圖

（2）位移分析

根據位移矢量圖可以看出，M1 模型開挖后邊坡受自重應力和地質構造影響坡體的位移方向主要朝向采坑臨空面（如圖6 所示），位移較大處為坡體中部范圍，最大值為0.09m。

圖6 M1 模型的位移矢量分布圖

（3）破壞區分析

M1 模型邊坡破壞主要表現為拉剪破壞，如圖7 所示。拉應力破壞區主要分布在坡頂，向坡體內延伸的最大深度約為30m；坡體中部以上坡面處也存在少量拉應力破壞區，最大深度約為18m。剪切破壞區主要分布在坡體上部巖體和坡腳。從坡頂往坡體內約20 ～30m 處開始向坡體內發展，最大延伸深度為55m；坡腳的剪切破壞區最大深度為22m。

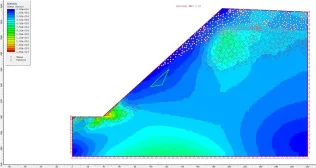
圖7 M1 模型的最大剪應變分布及拉剪破壞區域圖

（4）安全系數分析

最后利用強度折減法計算的安全系數為F=1.21，表明邊坡處于極限平衡狀態，在不受外界因素影響下是穩定的，符合一般規律，結果可靠。

（5）滑動機理分析

圖8～9 為M1 模型強度折減法計算安全系數的過程，從強度折減系數F 取值為1.0、1.18、1.21 和1.25 時計算出的邊坡最大剪應變和剪切破壞分布情況，可以看出，坡頂及坡腳發生剪切破壞，隨著折減系數增大，坡頂剪切破壞區范圍向巖體內擴展，坡腳破壞區逐步向上延伸，當折減系數增大到1.21 時，剪切破壞區在坡體內貫通，此時模型計算不收斂，滑面形狀為近似圓弧形，邊坡滑動失穩模式為圓弧滑動。當折減系數增大到1.25 時，邊坡沿著滑動面發生蠕變滑動，造成邊坡整體失穩。

圖8 M1 模型F=1.21 時最大剪應變分布圖

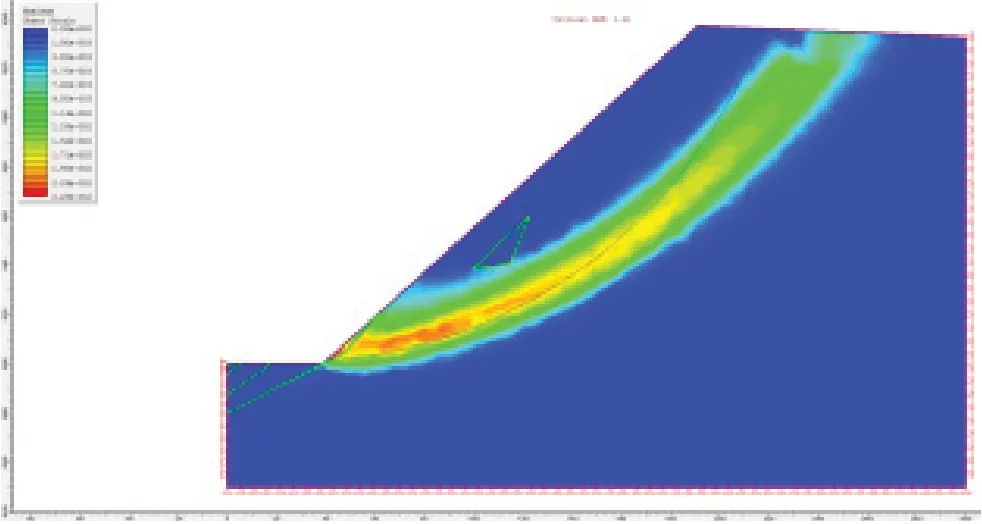
圖9 M1 模型F=1.25 時最大剪應變分布圖

5.2 M2 模型分析結果

（1）應力分析

通過對M2 模型的主應力等值線分布圖，如圖10 所示可以看出：最大應力值隨埋深的增加而增大，接近邊坡坡面時最大主應力值變小且呈順坡方向變化，在坡體的下部受開采臺階的影響，其應力的擾動狀態較大，坡面及坡面附近存在一定的拉應力，最大值的為0.4MPa。

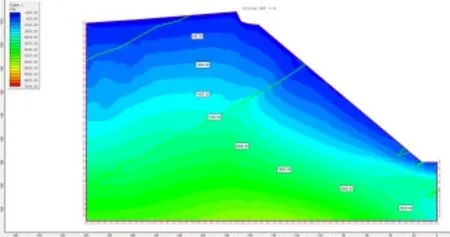
圖10 M2 模型的最大主應力等值線（σ1）分布圖

（2）位移分析

M2 模型開挖坡體的位移主要是向采坑臨空面移動（如圖11所示），位移較大處為坡體中部范圍，最大值為0.12m。

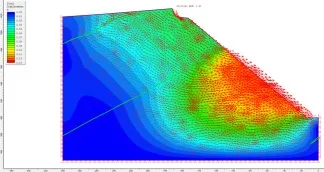
圖11 M2 模型的位移矢量分布圖

（3）破壞區分析

M2 模型坡體的破壞區主要為拉應力破壞區和剪切破壞區（如圖12 所示）。

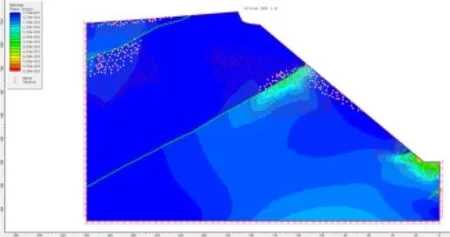
圖12 M2 模型的最大剪應變分布及拉剪破壞區域圖

拉應力破壞區主要分布在坡頂第四系內，最大深度約4.5m；坡體中部綠泥石英片巖向坡體內延伸最大深度約18m，在巖層交界處也存在部分拉應力破壞區。

剪切破壞區在坡頂、坡體中部和坡腳均有出現。坡頂向坡體內4.5m 的位置開始延伸最大深度為15m；坡體中部向坡體內延伸深度約為80m；坡腳最大深度約為22m。

（4）安全系數分析

強度折減法計算的安全系數為F=1.21，表明邊坡處于極限平衡狀態，在不受外界因素影響下是穩定的，符合一般規律，結果可靠。

（5）滑動機理分析

圖13～14 為M2 模型強度折減法計算安全系數的過程，從強度折減系數F 取值為1.18、1.21、1.22 和1.25 計算出的邊坡最大剪應變和剪切破壞分布情況，可以看出，邊坡坡頂坡體中部及坡腳均存在剪切破壞區，隨著折減系數增大，坡頂剪切破壞區范圍向巖體內擴展，坡腳剪切破壞區逐步向上延伸，坡體中部的剪切破壞區同時向坡頂和坡腳發展，當折減系數增大到1.21 時，坡體中部與坡腳的剪切破壞區貫通，邊坡中下部的綠泥石英片巖出邊坡產生滑動，滑面形狀為近似圓弧形，滑動模式為圓弧滑動。當折減系數增大到1.22 時，邊坡發生整體蠕變滑動，并進一步向坡體內發展。

圖13 M2 模型F=1.21 時最大剪應變分布圖

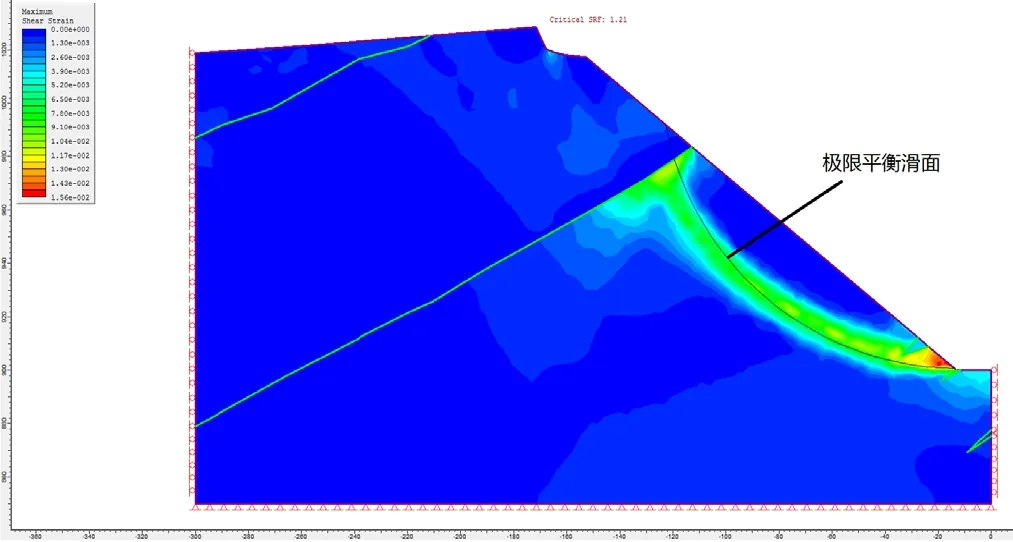
圖14 M2 模型F=1.22 時最大剪應變分布圖

3 總結

本文以巴彥哈爾金礦北露天邊坡為研究對象，采用強度折減法計算了63 線、71 線剖面邊坡安全系數，通過研究邊坡破壞模式，進而推測邊坡變形破壞規律，為邊坡治理提供依據。

選取具有典型意義的能反映巴彥哈爾金礦北露天邊坡穩定性的63 線（礦體下盤）和71 線（礦體上盤）工程地質剖面作為分析剖面。采用二維彈塑性有限元方法對這兩個剖面進行有限元計算分析，計算得出的安全系數為1.21，因此，建議整體邊坡角為當坑底標高為900 時，上盤40°，下盤42°。