深海采礦鋼結構塔架及底座平臺的穩定性分析

余倩 李文豪 楊高勝 陳丹東 謝夢琪

摘 要：深海采礦布放回收作業的負載大、重復性高、作業速度快、易受波浪和風力影響，可能造成鋼結構塔架和底座平臺的失穩。根據其工作特點，選取鋼結構塔架和底座平臺的三個典型截面，參照GB50017-2003《鋼結構設計規范》，分別進行整體穩定性理論折算計算、特征值（線性）屈曲和非線性屈曲有限元分析。結果表明，鋼結構塔架和底座平臺的整體結構穩定性較好，不會發生整體失穩。計算分析得到的臨界屈曲載荷值/屈曲極限載荷值可為深海采礦的鋼結構塔架和底座平臺的結構設計和載荷選取提供技術借鑒和工程經驗。

關鍵詞：深海采礦;鋼結構塔架;底座平臺;穩定性;屈曲分析

中圖分類號： TD98? 文獻標志碼：A

文章編號：1672-1098（2021）01-0056-06

收稿日期：2020-10-23

基金項目：國家重點研發計劃資助項目（2016YFC0304100）

作者簡介：余倩（1983-），女，湖北武漢人，高級工程師，碩士，研究方向：機械設計制造、船舶結構設計與優化。

Stability Analysis of Steel Structure Tower and? Base Platform for Deep-sea Mining

YU Qian1，2，LI Wenhao1，2，YANG Guaosheng1，2，CHEN Dandong1， XIE Mengqi1

（1. Ship Engineering Department， China Ship Development and Design Center， Wuhan Hubei 430064， China; 2. System Engineering Department， Wuhan Ship Development Design Institute， Wuhan Hubei 430064， China）

Abstract：The layout and recovery operation of deep-sea mining has characteristics of large load， high repeatability and fast operation speed， easy to be affected by wave and wind， which may cause instability of steel structure tower and base platform. Based on the national standard GB50017-2003 "Code for design of steel structures"， the overall stability theory conversion calculation， eigenvalue （linear） buckling and nonlinear buckling finite element analysis were performed on the three typical sections of the steel structure tower and the base platform selected according to the working characteristics . The results show that the overall structural stability of the steel structure tower and base platform is good. The critical buckling load value/buckling limit load value obtained by calculation and analysis will provide technical reference and engineering experience for the structural design and load selection of steel structure tower and base platform in deep-sea mining.

Key words：deep-sea mining; steel structure tower; base platform; stability; buckling analysis

自20世紀60年代以來，世界各國相繼進行了深海礦產資源開采裝備的研究[1]，我國在“十三五”期間立項國家重點研發計劃“深海多金屬結核采礦試驗工程”，該項目計劃研制一套3 500m水深的深海采礦試驗系統并完成不小于1 000m水深的海上整體聯動試驗[2]。鋼結構塔架及底座平臺是水面支持系統的重要組成部分[3]，其主體結構如圖1所示。布放回收過程負載大、重復性高、作業速度快、易受波浪和風力影響[4]，塔架和底座平臺在承載和作業時可能發生結構不穩定的現象，因此，對整體結構穩定性進行分析具有重要的實際意義和理論價值[5]。

文獻[6]基于ANSYS對井架進行了線性屈曲和非線性屈曲分析， 評估NDC-50DBT型石油鉆機井架的整體穩定安全性能， 結果表明相對于線性屈曲分析， 非線性屈曲分析的屈曲因子為線性屈曲因子的0.33～0.72倍。文獻[7]54通過對JJ170/42-K型井架的靜力分析、整體結構穩定性理論折算計算、線性屈曲分析和非線性屈曲分析，分別得出該井架的臨界載荷，分析出發生危險工況的地方，提高其在使用過程中的安全性。文獻[8]80通過對雙井架結構的靜力分析、動力分析和穩定性分析，并與單井架的力學性能進行對比，得到雙井架在靜、動力載荷下的應力變化規律，找到薄弱環節并提出改進措施。

深海多金屬結核采礦試驗工程對鋼結構塔架和底座平臺的承載能力、剛度、強度和穩定性提出較高的要求[9]。在工程中可以采用理論計算和計算機技術（有限元）相結合的方法對塔架和底座的整體結構穩定性進行分析和計算，為深海采礦的鋼結構塔架和底座平臺的結構設計和載荷選取提供技術借鑒和工程經驗。

1 失穩問題分析

在立柱上施加沿柱軸線作用的集中載荷，當載荷達到屈曲載荷Fpcr時，產生如圖中虛線所示的彎曲變形，此時彈性荷載撓度曲線如圖2（b）曲線a所示[7]64;隨著載荷的增加，二階彈塑性荷載撓度曲線為圖中曲線c所示，此時立柱呈現極值點失穩現象，其極限載荷值為F′pcr;若形成機構破壞時，二階剛塑性的曲線則為圖2（b）中曲線b所示，其臨界載荷為Fpu[8]59。

2 穩定性理論折算的計算

2.1 設計規范中的穩定性計算方法

參照GB50017-2003《鋼結構設計規范》中第5章中的相關內容，在引入實腹式軸心受壓構件的整體穩定性的基礎上對壓彎構件的穩定性問題進行分析和計算。

1）實腹式軸心受壓構件的整體穩定性計算

實腹式軸心受壓構件的整體穩定性計算公式為

σ=Nφ·A≤f（1）

式中：N為構件的軸心力;φ為軸心壓桿的穩定性系數;A為壓桿的截面面積;σ為穩定強度;f為抗壓強度設計值。

2）壓彎構件的穩定性計算

①彎矩作用在對稱軸平面內（繞x軸）的實腹式壓彎構件穩定性應按下列公式計算

Nφx·A+βmxMxγxW1x（1-0.8NN′EX）≤f（2）

式中：N′EX為參數，N′EX=π2EA/（1.1λx2）;φx為彎矩作用平面內的軸心受壓構件穩定系數;Mx為所計算構件段范圍內的最大彎矩;

W1x為在彎矩作用平面內對較大受壓纖維的截面模量;βmx為等效彎矩系數。

②彎矩繞虛軸（x軸）作用的格構式壓彎構件，其彎矩作用平面內的整體穩定性應按下式計算

Nφx·A+βmxMxW1x（1-φxNN′EX）≤f（3）

③彎矩作用在平面外的穩定性計算與實腹式構件相同，在此不再贅述。

④換算長細比

換算長細比按下列公式計算

λ0x=λx2+40AA1x（4）

λ0y=λy2+40AA1y（5）

式中：A1x為構件截面中垂直于x軸的各桿件毛截面面積之和;A1y為構件截面中垂直于y軸的各桿件毛截面面積之和。

綜合以上分析和研究，對于壓彎構件在分析其穩定性時需計算彎矩作用平面內和彎矩作用平面外兩種情況，計算時需根據結構的最大彎矩、截面模量和相關系數等參數來確定。

2.2 穩定性理論折算的計算

鋼結構塔架是由多個桿件組合成的桁架結構，底座平臺是格構式壓彎構件，綜合考慮其結構特征和受力特點[10]，采用整體穩定性計算方法，按實腹式壓彎構件穩定性計算公式，進行塔架和底座平臺的整體穩定性理論計算[11]。

在塔架和底座平臺上截取3個橫截面進行分別計算，以最大值截面的計算結果為下一步有限元仿真分析的基礎和依據。3個截面選取如圖3所示。

1）A-A截面穩定性理論折算的計算

以A-A截面為例，計算公式如下

σ=Nφx·A+βmxMxγxW1x（1-0.8NN′EX）≤f（2）

①查GB50017-2003《鋼結構設計規范》中表3.4.1-1鋼材的強度設計值（N/mm2）中，Q345鋼、厚度35～50mm的抗拉、抗壓和抗彎強度為f=265N/mm2。

②根據GB50017-2003《鋼結構設計規范》中表4.1.1中，對工字形截面，γx=1.05，γy=1.20;對箱形截面，γx=γy=1.05。

③根據GB50017-2003《鋼結構設計規范》5.2.2中，有端彎矩和橫向載荷同時作用時，使構件產生同向曲率時，βmx=1.0;產生反向曲率時，βmx=0.85。

④經計算，長細比λx=λy=27。

⑤毛截面面積A=4×（190+2×97.2）=1 537.6cm2=153 760mm2。

⑥查《機械設計手冊》第1章表2.1-87熱軋H型鋼尺寸規格，取Wx=4×（2 220+2×1 198）=18 464cm3=18 464 000mm3。

⑦按照GB50017-2003《鋼結構設計規范》中附錄B.5受彎構件整體穩定系數的近似計算，當λy≤120235/fy時，工字形截面（含H型鋼）雙軸對稱時，φx=1.07-λy244 000·fy235=1.07-27×2744 000×355235=1.045。當φx值大于1.0時，取φx=1.0。

⑧按照GB50017-2003《鋼結構設計規范》第5章5.2.2中，NEX′=π2EA/（1.1λx2），查表3.4.3鋼材和鑄件的物理性能指標，取E=206×103N/mm2。NEX′=3.142EA1.1λx2=3.142×206×103×153 7601.1×272=3.895×108N

⑨最大彎矩Mx=5 850×103×495=2.896×109N·mm

將以上①～⑨代入計算公式

σ=NφxA+βmxMxγxW1x（1-0.8NNEX′）=5.85×1061×1.54×105+0.85×2.896×1091.05×1.85×107×（1-0.8×5.85×1063.9×108）=38+128.6=166.6N/mm2<265N/mm2

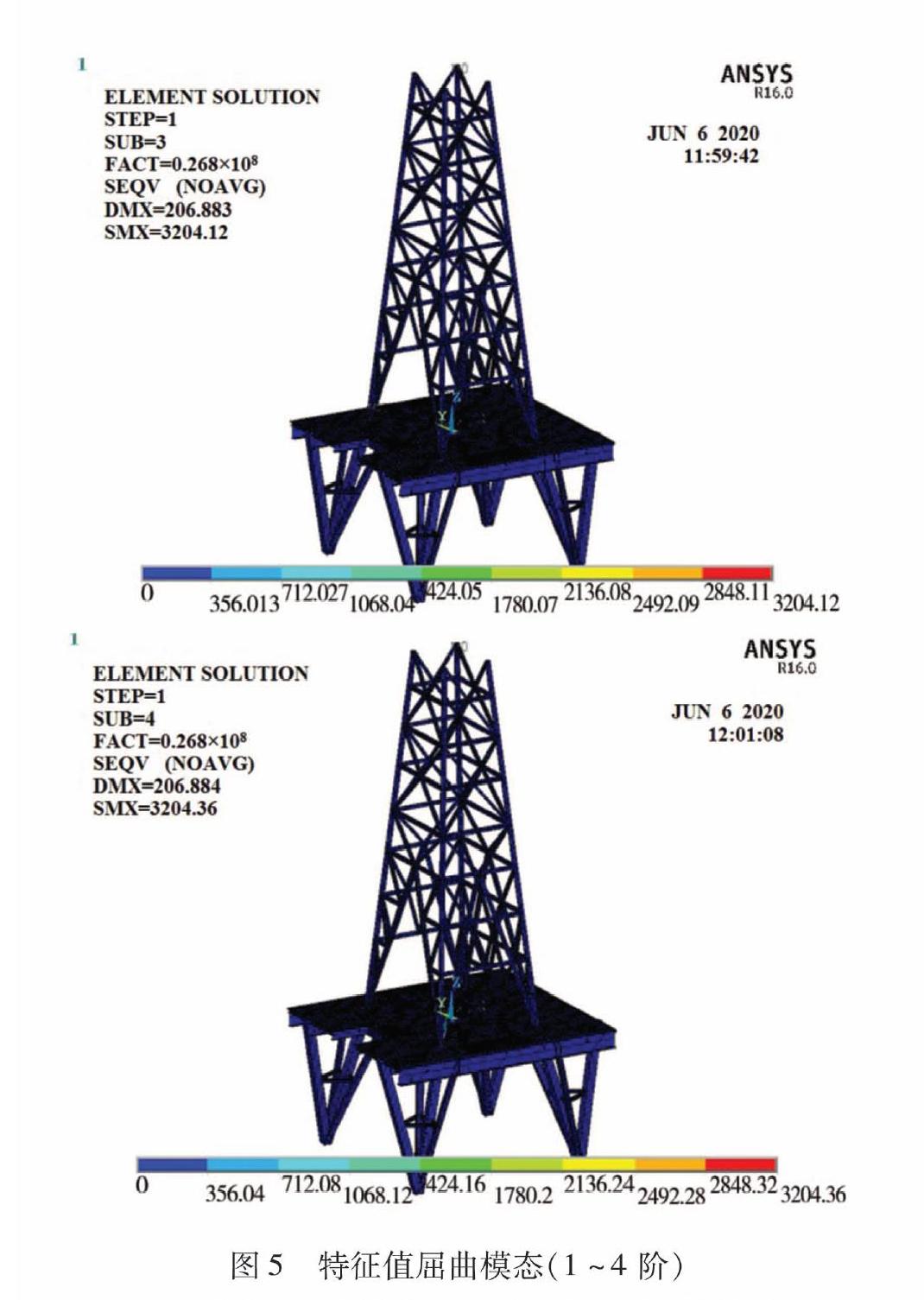
σ

取f=265N/mm2反推線性屈曲的臨界載荷P′=20 972 864N=20 972kN。

2）B-B截面穩定性理論折算的計算

同上，計算B-B截面的穩定強度σ=111.2N/mm2<265N/mm2。

σ

3）C-C截面穩定性理論折算的計算

計算C-C截面的穩定強度σ=22.4N/mm2<265N/mm2。

σ

以上計算結果表明，鋼結構塔架及底座平臺的整體結構穩定性較好，不會發生整體失穩。

3 穩定性有限元仿真分析

3.1 特征值（線性）屈曲分析

單元剛度矩陣[K]e和單元幾何剛度矩陣[Kg]e可以集成整個結構剛度矩陣[K]和幾何剛度矩陣[Kg]，并形成平衡方程為

（[K]+λ[Kg]）{δ}={P}（6）

式中：λ為待定的比例因子。

所以若{δ}={0}，滿足以上方程式，表示沒有受到外界的影響，或雖然受到外界的影響但又可以恢復到原來的平衡狀態[12]。

若假設結構處于某種臨界狀態，即{δ1}中所有的數不全為零，但是仍然能夠滿足平衡條件，此時這個方程式的系數行列式必須等于零，即

[K]+λ[Kg]=0（7）

這就是穩定方程，求解方程得到特征值λcr，則可得到

{Pcr}={P}×λcr（8）

因此可得到臨界載荷Pcr[13]。

在ANSYS分析軟件中建立鋼結構塔架及底座平臺的有限元模型，設置預應力并執行1次靜力分析，計算屈曲模態和擴展模態[14]。對底座平臺的支腿與船舶甲板安裝連接處施加剛性固定的邊界條件。在天車中心處建立1個獨立點（MPC），將塔架頂端的節點自由度與其關聯，建立剛性域[15]。在MPC點施加預應力為-1 N，設置擴展模態值為1，比例系數為1。前6階特征值屈曲分析的計算結果如圖4所示。前4階特征值屈曲模態如圖5所示。

通過有限元計算方法，可以得到鋼結構塔架及底座平臺的失穩臨界載荷（一階屈曲載荷）為Pcr=0.223×108N=22 341kN，也就是說，當塔架及底座平臺的載荷與失穩臨界載荷相等時，塔架及底座平臺結構就會出現失穩的現象[16]。這時塔架及底座平臺的變形將迅速變大，結構會喪失平衡狀態，位移開始增大，直至第三階時發生整體失穩甚至坍塌[17]。而塔架及底座平臺的最大靜鉤載為5 850kN，為臨界失穩載荷Pcr的1/4，未達到臨界失穩載荷，因此，鋼結構塔架及底座平臺不會出現整體失穩的問題。可以看出有限元分析計算出的結果與穩定性理論折算法計算的結果是相同的。

通過有限元分析計算得到的臨界失穩載荷Pcr=22 341kN，與理論折算法計算得出線性屈曲臨界載荷P′=20 972kN，結果幾乎相同，兩個計算結果相差僅約6.5%。說明通過理論折算法和特征值屈曲有限元分析法對鋼結構塔架及底座平臺的屈曲分析結果是可以相互印證的，計算結果是基本正確的。

3.2 非線性屈曲分析

非線性屈曲分析是用一種逐漸增加載荷的非線性靜力分析得出使結構開始變得不穩定時的極限載荷，在加載過程中慢慢增加一個不變的載荷增量值，同時該增量值使得到的結果發散，最終得到預期的臨界載荷[18]。

由結構增量形式的平衡方程可知，加載時如果將極限載荷分級加載，第i級載荷的增量為d{F}i，可以得到下式

（[K-0]i+[K-L]i+[K-σ]i）d{Δμ}i=[K-T]id{Δμ}i=d{F}i（9）

式中：d{Δμ}i為第i次加載d{F}i產生的節點位移增量;[K-T]i為第i次加載時的雙重非線性分析的切線剛度矩陣。

當所加的載荷增量增加到接近整體結構發生不穩定的情況時，此時產生的是極限載荷，迭代將會不收斂，通常情況下，就會認為此時已經達到結構極限承載能力[19]。

在進行有限元分析時應注意以下幾點：①在模型上加載初始的擾動或初始的缺陷，將一階屈曲模態變形作為初始缺陷，使計算更準確;②打開大變形效應分析，激活應力剛化;③打開弧長法，對載荷子步進行迭代求解[20]。

非線性屈曲分析結果如圖6～圖7所示。

由以上結果可以看出，鋼結構塔架的非線性屈曲極限載荷P″=21 100kN，即為圖7中拐點所對應的縱坐標的數值，超過這個極限載荷后，塔架及底座平臺結構也失去了繼續加載的能力，結構慢慢會不平衡，在時間到達某一個值時，塔架和底座平臺結構的穩定性就會遭到破壞。

比較特征值（線性）屈曲的臨界失穩載荷Pcr=22 341kN與非線性屈曲的極限載荷P″=21 100kN，結果幾乎相同，兩個計算結果相差僅約5.9%，其中，非線性屈曲分析的結果誤差較小，相對更加準確可靠。

4 結論

（1）對鋼結構塔架和底座平臺進行整體穩定性理論折算的計算，結果表明鋼結構塔架和底座平臺的整體結構穩定性較好。

（2）采用特征值（線性）屈曲和非線性屈曲兩種方法對鋼結構塔架和底座平臺進行有限元計算分析，失穩臨界載荷/屈曲極限載荷均遠大于結構最大靜鉤載，表明鋼結構塔架不會發生整體失穩。

（3）對比整體穩定性理論折算、特征值（線性）屈曲和非線性屈曲3種分析方法的計算結果，發生大變形的部位均是塔架頂部;失穩臨界載荷/屈曲極限載荷數值相差較小，可相互印證，其中非線性屈曲分析的結果誤差較小，相對更加準確可靠。

參考文獻：

[1] D A IUNGEMEISTER，R I KOROLEV，S L SERZHAN，et al.Materials of devices and equipment for deep-sea mining of manganese resources[J].Journal of Physics： Conference Series， 2020，1 582（1）： 012098.

[2] 李向陽.我國深海多金屬結核采礦試驗之初論[J].海洋開發與管理，2017（1）：63-66.

[3] 楊高勝， 陳丹東， 李文豪，等. 基于管道水力提升式采礦系統的深海采礦船總體設計研究[J]. 船舶工程，2019，41（1）：23-33.

[4] 喬長奎， 郝奉禹， 華小濤. JJ675/48-K型井架有限元及應力測試對比分析[J]. 石油礦場機械，2016，45（6）：31-36.

[5] 劉孔忠， 葛運春， 周國強， 等. 海洋鉆機底座承載性能的試驗研究和有限元分析[J]. 中國工程機械學報，2015，13（4）：367-371.

[6] 盛尹， 熊峰， 葛琪. 基于ANSYS的石油井架整體穩定性分析[J]. 四川建筑，2016，36（1）：128-131.

[7] 潘娜娜. JJ170型鉆機井架的整體結構穩定性分析方法[D]. 蘭州：蘭州理工大學，2013.

[8] 紀蘇丹. 海洋雙井架結構力學性能研究[D].成都：西南石油大學，2015.

[9] QINGHUI SONG， HAIYAN JIANG， QINGJUN SONG，et al.Longitudinal vibration compensation model of stepped-pipe strings in deep-sea mining[J]. National Library of Medicine， 2020， 15（11）： e0241650.

[10] GENCERFUNDA，HAMAMCIOGLU-TURAN MINE，AKTASENGIN.Structural vulnerability of ancient dry masonry towers under lateral loading[J].Journal of Archaeological Science：Reports，2020，34（9）：102663.

[11] 李成晨， 張文彬， 劉曉輝，等. 微觀氣象條件下風力發電機組塔架載荷響應分析[J]. 機械設計與制造工程，2020，49（10）：102-108.

[12] 陳宇海， 吳文秀， 都亞男，等. 在役海洋修井機底座承載能力評估技術研究[J]. 石油機械，2015，43（6）：50-54.

[13] 鄭鴻生， 歐開良. 基于有限元法的塔架結構數值模擬分析[J]. 現代制造技術與裝備，2020，56（10）：23-28.

[14] ZHENGRONG WU， HAO WANG， WENHUI YU， et al. 3D HIGH-EFFICIENCY AND HIGH-PRECISION MODEL-DRIVEN MODELLING FOR POWER TRANSMISSION TOWER[J].The International Archives of the Photogrammetry， Remote Sensing and Spatial Information Sciences， 2020， XLIV-4/W3-2020： 421-426.

[15] 張亮. 某自升式平臺生活模塊底座螺栓斷裂失效分析及加強結構[J]. 石油化工設備，2020，49（6）：74-79.

[16] 劉丹丹. 深水半潛式平臺鉆機前開口井架的穩定性分析[D].成都：西南石油大學，2015.

[17] 陶尼斯， 李成君， 張勇，等. 深海采礦船關鍵設備加強直接計算與優化設計[J]. 船舶，2020，31（4）：23-30.

[18] 李家來， 謝宇新. 深海浮標塔架的力學響應研究[J]. 應用力學學報，2020，37（5）：2 037-2 322.

[19] 丁慧， 楊兆建， 王淑平，等. 垂直救援提升系統井架的設計與有限元分析[J]. 煤炭技術，2016，35（7）：247-249.

[20] 邴通林. 直升機吊裝模塊鉆機底座設計與研究[J]. 機電工程技術，2018，47（7）：178-180.

（責任編輯：丁 寒，吳曉紅）