應用改進RBF神經網絡的室內環境舒適度評價

楊亮，王誼

(陜西工業職業技術學院 航空工程學院，陜西 咸陽 712000)

0 引言

隨著生活水平不斷改善，人們對生存環境關注度越來越高，室內環境與人們生活息息相關，室內環境好壞直接影響到人們生活質量[1-3]。對室內環境相關參數進行監測，為改善室內環境具有重要的意義。室內環境的舒適度是室內環境質量好壞衡量參數，室內環境舒適度高可以保證人們的身心健康，因此對室內環境舒適度評價進行科學、客觀評價顯得十分緊迫和重要[4-6]。

室內環境舒適度主要指室內環境對人的適宜程度，具有很強的主觀性。近年來，隨著電子技術、自動化技術、傳感器技術以及網絡技術的發展和融合，室內環境舒適度已經進行入了智能評價階段，評價結果更加科學[7-9]。如出現了基于模糊理論的室內環境舒適度評價模型、基于人工神經網絡的室內環境舒適度評價模型等[10-11]，由于室內環境舒適度具有一定的時變性，而模糊理論是一種線性建模技術，因此模糊理論的室內環境舒適度評價偏差比較大；人工神經網絡是一種模仿人類大腦神經網絡的信息處理系統，能夠以任意精度逼近任何非線性問題的解，因此成為室內環境舒適度評價的主要研究方向，尤其徑向基函數(RBF)的應用范圍最為廣泛。在RBF神經網絡的室內環境舒適度評價過程中，其參數值的選擇直接關系到室內環境舒適度評價結果，傳統方法采用人工方式確定，這樣難以建立最優的室內環境舒適度評價模型，室內環境舒適度評價結果不穩定[12-14]。

為了提高室內環境舒適度評價精度，針對RBF神經網絡參數優化問題，提出了改進RBF神經網絡的室內環境舒適度評價模型，該模型通過引入粒子群算法確定最優RBF神經網絡參數，從而實現高精度的環境舒適度評價，并通過具體測試實驗分析其有效性和優越性。

1 改進RBF神經網絡的室內環境舒適度評價模型

1.1 建立室內環境舒適度評價指標體系

M表示人體熱量代謝；W表示人體所做的機械功，在穩定條件下，人體平衡狀態的儲備熱量為式(1)。

S=M-W-E-R-C

(1)

式中，E表示汗水蒸發帶走的熱量；R表示人體表面與外界環境的交換熱量；C表示人體表面和外界環境的對流交換熱量。

當S=0時，人本熱達到了平衡狀態，那么舒適度為式(2)—式(5)。

PMV=((0.3.3e-0.036M+0.028){M-W-3.05×10-5[5 733-6.99(M-W)-Pa]-0.42[M-W-58.15]-1.7×10-5M(5 867-Pa)-0.001 4M(34-ta)-3.96×10-8fcl[(tcl+273)4-(tr+273)4]-fclhc(tcl-ta)}

(2)

(3)

tcl=35.7-0.028(M-W)-Icl{3.96×10-8fcl[(tcl+273)4-(tcl+273)4]+fclhc(tcl-ta)}

(4)

(5)

式中，Pa表示空氣壓力；ta表示氣溫；tr表示環境輻射溫度；Va表示空氣流動速度；fcl表示衣服表面系數；Icl表示衣服熱阻；tcl表示衣服表面溫度；hc表示人體表面傳熱系數。

根據相關文獻研究，室內環境舒適度評價指標主要為：室內溫度(x1)、室內光照(x2)、室內濕度(x3)和室內噪聲(x4)。室內環境舒適度等級劃為4個等級，分別如表1所示。

表1 室內環境舒適度等級劃分

1.2 RBF神經網絡

RBF神經網絡和其它神經網絡一樣，是一種多層結構，典型的結構為3層結構，3層結構分別為：輸入層、隱含層、輸出層，每一層包含多個神經元節點，同一層的神經元節點之間沒有聯系，但是相鄰層神經元節點之間存在一定的聯系。設第i個神經元節點的輸入為Xi(i=1,2,…,n)，第j個神經元節點輸出為Yj(j=1,2,…,m)，隱含層中心向量為cj(j=1,2,…,nc)，則RBF神經網絡的輸出為式(6)。

(6)

式中，wij為隱含層與輸出層的神經元節點之間的連接權值；wi0為第i個節點的閾值；Yij為第i個節點的輸出；nc為隱層節點個數；f為映射函數。

徑向基函數作為隱含層的映射函數，如式(7)。

(7)

式中，σi表示核寬度。

采用RBF神經網進行室內環境舒適度評價時，參數wij、ci和σi取值直接影響室內環境舒適度評價精度，傳統RBF神經網絡采用經驗方法確定，具有一定的盲目性，無法建立最優的室內環境舒適度評價模型，為此本文采用粒子群算法改進RBF神經網絡參數確定的方法，以提升室內環境舒適度評價精度。

1.3 粒子群算法

粒子群算法包含多個粒子，這些粒子組成種群，每一個粒子具有一個位置向量和速度向量，對于第i個粒子，位置向量和速度向量分別為Xi=[xi,1,xi,2,…,xid]和Vi=[vi,1,vi,2,…,vid]，Pi和gi為第i個粒子和種群的歷史最優位置，速度和位置更新方式為式(8)。

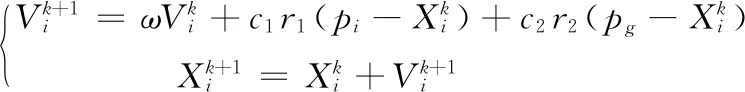
(8)

2.4 改進RBF神經網絡的室內環境舒適度評價步驟

Step1：建立室內環境舒適度評價指標體系，并對它們的數據進行采集，確定室內環境舒適度等級，其和室內環境舒適度評價指標組成樣本集合。由于室內環境舒適度評價單位不一樣，因此對它們進行歸一化操作，使它們的值均縮放到[0 1]之間，如式(9)。

(9)

Step2：根據室內環境舒適度評價指標數量和舒適度等級構建RBF神經網絡的結構。由于指標數為5個，那么輸入層的節點數為4，隱含層的節點為9，輸出層節點為4。

Step3：設置粒子群算法的相關參數如下：粒子群數量M；加速系數c1、c2；最大迭代次數Tmax。

Step4：初始化粒子群，每一個粒子代表一組參數wij、ci和σi。

Step5：計算每一個粒子的適應度函數值，本文的適應度函數采用室內環境舒適度評價精度進行構建，如式(10)。

(10)

Step6：迭代次數增加，粒子群不斷更新位置和速度，當達到最大迭代次數時，根據最優粒子的位置得到RBF神經網絡參數wij、ci和σi的最優值。

Step7：RBF神經網絡根據參數wij、ci和σi的最優值對室內環境舒適度評價訓練樣本進行學習，建立最優的室內環境舒適度評價模型。

2 室內環境舒適度評價的仿真測試

2.1 測試對象

為了分析改進RBF神經網絡的室內環境舒適度評價模型的性能，選擇某一個酒店會議室作為測試對象，該會議室長、寬、高分別為50米、20米、3.5米，安裝了空調，空間結構如圖1所示。

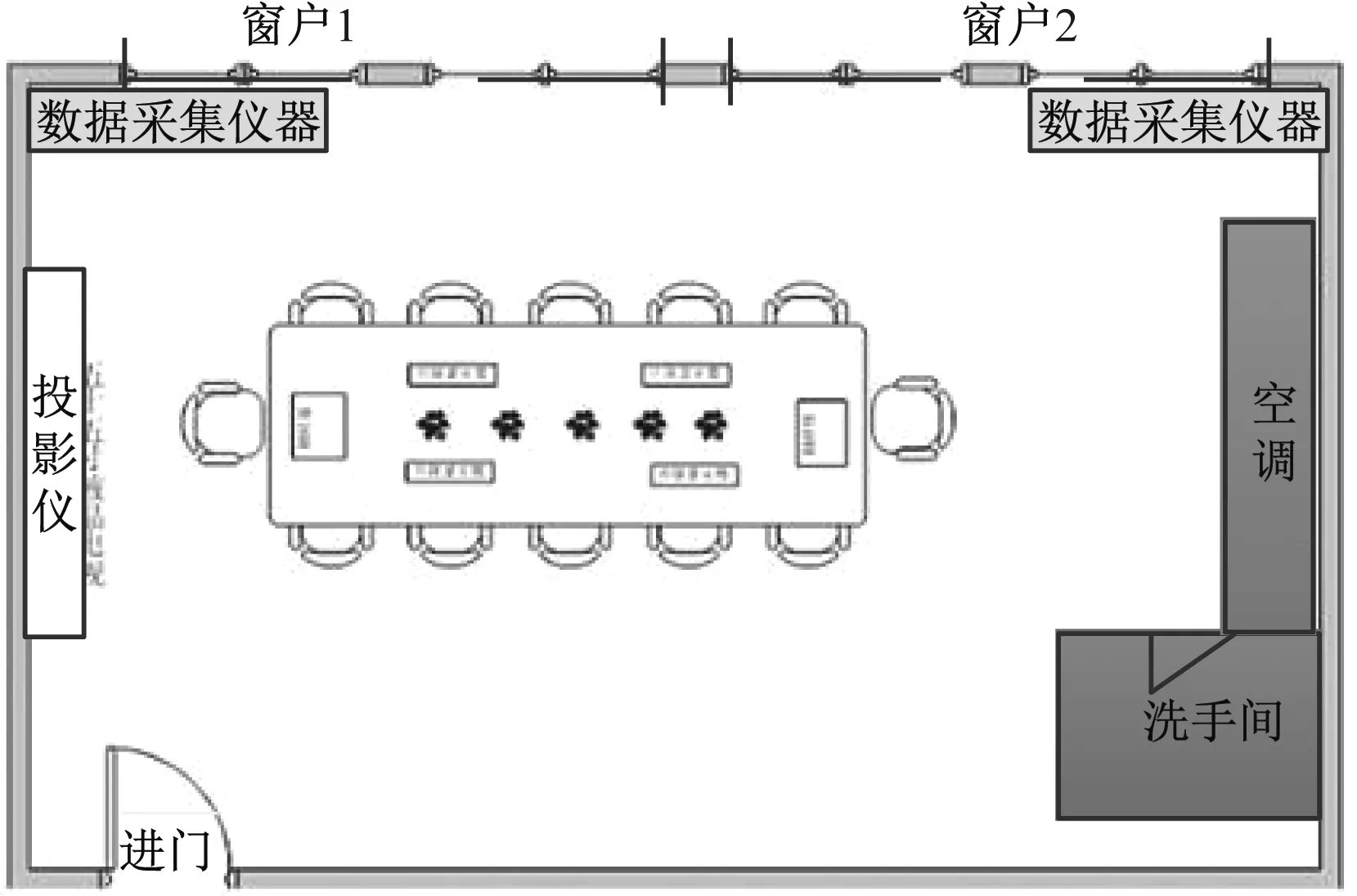
圖1 室內環境舒適度評價的對象平面圖

通過數據采集儀器，如：溫度傳感器、濕度傳感器等對該會議室的內環境舒適度評價相關數據進行采集，共采集100個樣本數據，RBF神經網絡的最大迭代次數為500次。具體如表2所示。

表2 室內環境舒適度評價實驗的相關數據

2.2 與傳統RBF神經網絡的室內環境舒適度評價結果比較

為了體現實驗的公平性，共進行5次仿真實驗，每一次仿真實驗從表1中隨機選擇60個樣本作為訓練樣本，剩下樣本作為測試樣本，其中室內環境舒適度評價指標值作為RBF神經網絡輸入，室內環境舒適度值作為輸出，通過RBF神經網絡的訓練，并采用粒子群算法優化RBF神經網絡的參數，建立室內環境舒適度評價模型，對測試樣本進行評價，并選擇傳統RBF神經網絡作為對比模型，該模型參數憑經驗方式確定，兩種模型的的室內環境舒適度評價精度如圖2所示。

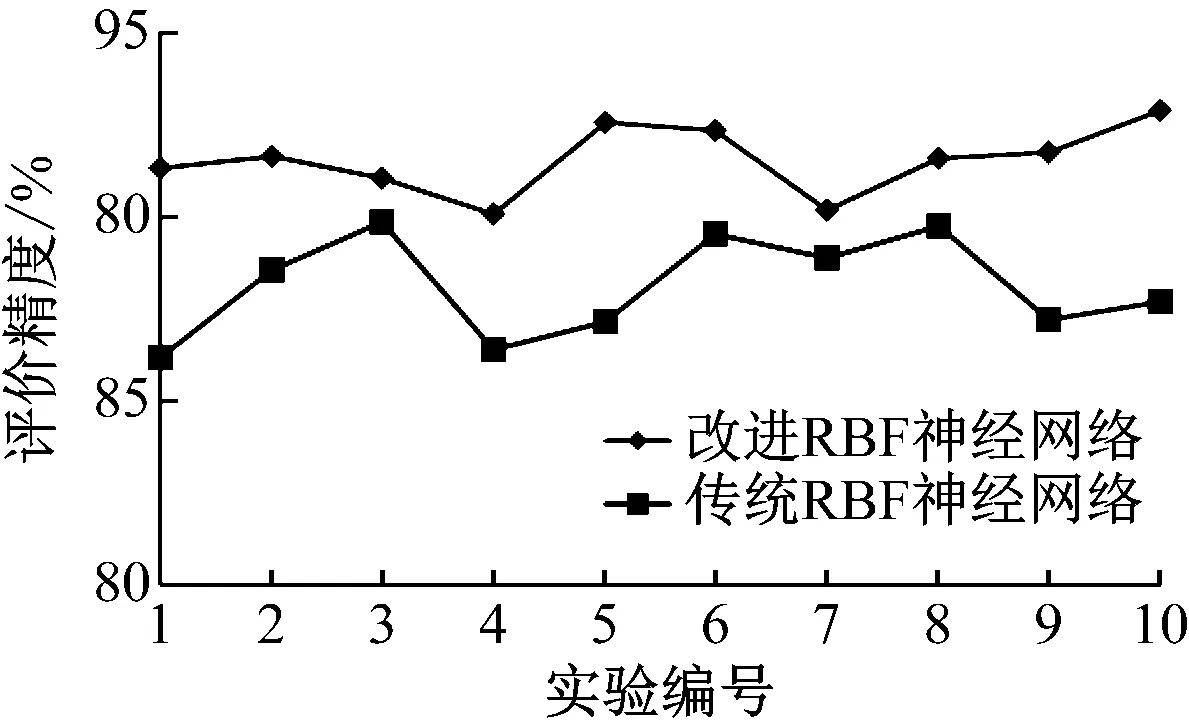
圖2 與傳統RBF神經網絡的室內環境舒適度評價精度比較

從圖2可以看出，相對于傳統RBF神經網絡，改進RBF神經網絡的室內環境舒適度評價精度得到大幅度提升，這主要是由于本文模型通過引入粒子群算法找到了最優的RBF神經網絡參數，克服了當前室內環境舒適度評價模型參數優化難題，減少了室內環境舒適度評價誤差，室內環境舒適度評價結果更加可靠。

2.3 與經典室內環境舒適度評價模型的性能比較

為了分析改進RBF神經網絡的室內環境舒適度評價模型的優勢，選擇文獻[10]的室內環境舒適度評價方法和文獻[11]的室內環境舒適度評價方法進行對比測試實驗，統計每一種模型在不同時間點的室內環境舒適度評價誤差(%)，結果如圖3所示。

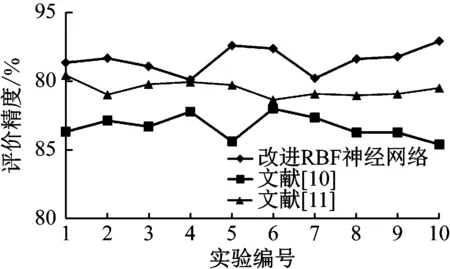
圖3 與經典模型的室內環境舒適度評價精度比較

對圖3的室內環境舒適度評價誤差進行比較和分析可以發現，改進RBF神經網絡的室內環境舒適度評價誤差明顯少于對比模型，提升了室內環境舒適度評價精度，獲得了更優的室內環境舒適度評價結果。

3 總結

為了解決當前各種室內環境舒適度評價方法存在的局限，以改善室內環境舒適度評價精度為目標，設計了基于改進RBF神經網絡的室內環境舒適度評價模型，將室內環境舒適度評價指標值作為RBF神經網絡的輸入，室內環境舒適度等級作為RBF神經網絡的期望輸出，通過RBF神經網絡的智能學習功能，擬合輸入和輸出之間的變化關系，并通過引入粒子群算法解決RBF神經網絡參數優化問題，克服了傳統RBF神經網絡的不足，最后與其它室內環境舒適度評價模型的對比結果表明，改進RBF神經網絡的室內環境舒適度評價精度高，并且室內環境舒適度評價更加可靠，具有較高的實際應用價值。