基于水動力模型的城市河道堤防安全評估方法研究

劉 葉，丁龍翔

(廣州市增城區(qū)水務(wù)局，廣州 510000)

0 引 言

水動力模型是一種描述水流受力與運動相互關(guān)系的數(shù)學(xué)模型，使用模型內(nèi)流體力學(xué)的基本方程，數(shù)值模擬流動水的動力遷移過程[1]。在城市化建設(shè)下，城市用水不斷增加，對城市河道堤防的安全防護已經(jīng)成為當下的研究重點，安全評估城市河道堤防的狀態(tài)，能夠為實際河道的防護工作提供一定的數(shù)據(jù)支持。為此，在水動力模型的參與下，構(gòu)建一種城市河道堤防安全評估方法。綜合城市空間內(nèi)的降水量以及堤防潰堤的數(shù)值，不斷探究不同河堤位置的匯流條件[2]。在構(gòu)建城市河道堤防安全評估方法上，在進入21世紀后，國外研究人員在有限元分析方法的支持下，構(gòu)建得到多種水動力分析模型，并在多個潰堤的數(shù)值控制下，分析得到多個臨界系數(shù)[3]。我國研究水動力模型起步較晚，在上個世紀90年代初期，相關(guān)研究人員采用TVD格式，預(yù)測得到適應(yīng)性較強的高性能算法，并應(yīng)用到實際河道處理工作中。

1 基于水動力模型的城市河道堤防安全評估方法研究

1.1 水動力耦合城市河道流量

城市河道內(nèi)的水位較為穩(wěn)定，所以在水動力耦合城市河道水位時，采用垂向耦合的方式處理河道堤防中的水流[4]，采用水動力模型將城市的排水管看作為河道堤防的組成部分。針對一維管網(wǎng)結(jié)構(gòu)節(jié)點，計算管道節(jié)點間的交換流量，計算公式為：

(1)

式中：Qn為管道節(jié)點處的交換流量數(shù)值；c0為管道口的出流系數(shù)；Amh為管道節(jié)點間的交換面積；H1D為管道1的流量數(shù)值；H2D為管道2的流量數(shù)值；g為重力常數(shù)。

在管道外部雨水的影響下，管網(wǎng)相交處產(chǎn)生了一部分的節(jié)點回流，此時節(jié)點回流為：

(2)

式中：cw為堰流系數(shù)；w為堰流寬度；其余參數(shù)含義不變。

在上述水流數(shù)值的控制下，不同城市河道在不同位置存在透水區(qū)和不透水區(qū)[5]，以式(1)、式(2)中涉及數(shù)值作為經(jīng)驗初始值，設(shè)定耦合過程的參數(shù)，見表1。

在水動力模型中，設(shè)定表1耦合參數(shù)后，計算河道中的流量數(shù)值，計算公式為：

表1 設(shè)定的耦合參數(shù)

(3)

式中：Hmax為河堤內(nèi)的最高水位數(shù)值；其余參數(shù)含義不變。

以式(3)處理得到的城市河道水流量作為數(shù)值基礎(chǔ)，計算河道堤防匯流過程堤防產(chǎn)生的變化。

1.2 計算河道堤防匯流

將上述計算得到的水流量數(shù)值作為河道堤防運行正常數(shù)值[6-7]，在計算河道堤防匯流時，根據(jù)堤防土壤表面因降雨產(chǎn)生的自由水流，河道堤防產(chǎn)生了一定數(shù)值的干擾流量，產(chǎn)生干擾流量的過程見圖1。

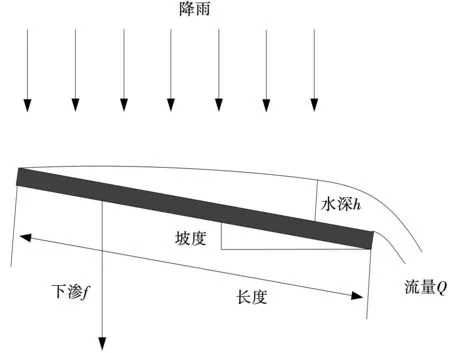
圖1 產(chǎn)生干擾流量的過程

在圖1產(chǎn)生干擾流量的過程中，以河道堤防產(chǎn)生的坡度數(shù)值[8-9]，計算堤防儲存量與通量的關(guān)系，計算公式為：

Q=αhm

(4)

式中：Q為河道堤防單位寬度自由水的流量數(shù)值；α為河道坡度的影響參數(shù)；m為河道表面糙率參數(shù)。

所以，此時堤防在降水過程中水流的連續(xù)方程為：

(5)

式中：t為降雨時間；x為水流沿坡度方向的距離；q(x,t)為側(cè)向入流參數(shù)；其余參數(shù)含義不變。

控制形成的水流在河堤的上流邊界處[10]，控制方程可表示為：

(6)

式中：u為河道上游；w為河堤單元寬度；L為河堤單元長度；其余參數(shù)含義不變。

根據(jù)上述計算公式可知，控制河道堤防上游處的匯流方向為側(cè)向入流后，河堤的邊界將外部雨水轉(zhuǎn)化為河道內(nèi)的匯流[11]。將上述處理過程作為評估對象，構(gòu)建一個河道堤防的安全評估過程。

1.3 實現(xiàn)安全評估

綜合上述處理過程涉及的各項數(shù)值指標，整合上述指標為一個數(shù)據(jù)集合G={g1,g2,…,gn}。根據(jù)專家對上述數(shù)據(jù)的評價意見，定義專家評價的范數(shù)，計算公式為：

(7)

式中：p為評價專家的數(shù)量。

將前述處理的各項指標作為基礎(chǔ)層，將專家評價得到的范數(shù)作為安全層。在構(gòu)建安全評估方法時，針對兩個不同的層次建立評價過程[12-13]。前述處理得到的指標，間接影響了河道堤防的安全，所以基礎(chǔ)層的評估過程可表示為：

(8)

式中：j為河道堤防數(shù)值指標的數(shù)量；b為指標的屬性參數(shù)；其余參數(shù)含義不變。

在該基礎(chǔ)層評估過程下，將專家評價的范數(shù)與式(8)聯(lián)立處理，最終河道堤防的安全評價過程可表示為：

(9)

式中：wi為專家評價參數(shù)權(quán)重數(shù)值；其余參數(shù)含義不變。

在上述處理過程下，在實現(xiàn)對城市河道堤防安全評估時，綜合考慮專家范數(shù)，不斷優(yōu)化安全評估方法的安全可靠性[14-15]。綜合上述處理，最終完成對基于水動力模型的城市河道堤防安全評估方法的研究。

2 實 驗

2.1 實驗準備

隨機選取一處城市河道堤防作為實驗對象，在河堤的走勢處設(shè)定12處測試點，設(shè)定的測試點見圖2。

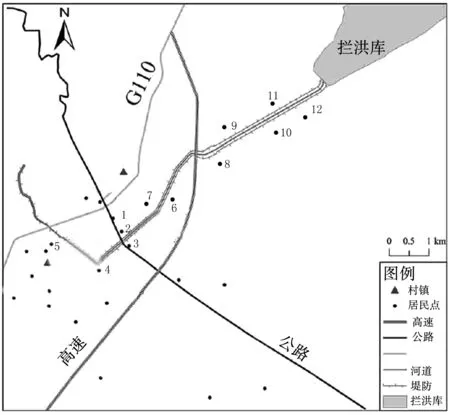
圖2 選定的城市河道

在圖2所示的城市河道內(nèi)，根據(jù)該測試點的歷史數(shù)據(jù)，定義測試點的成災(zāi)水位。實際的成災(zāi)水位見表2。

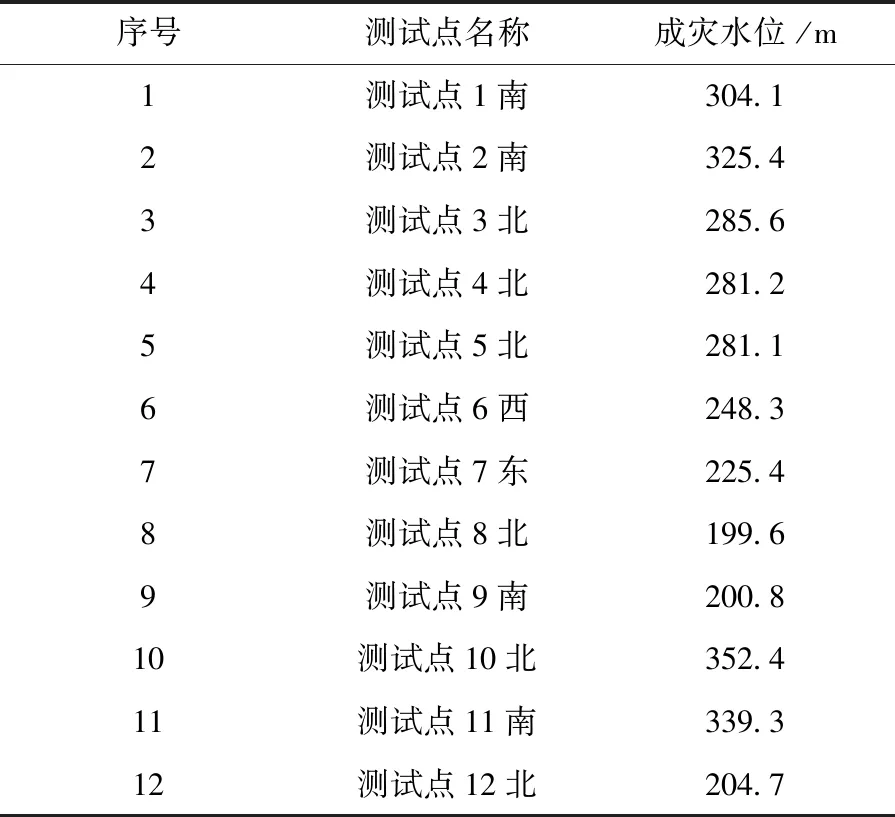
表2 設(shè)置測點的成災(zāi)水位

由表2中測試點成災(zāi)水位數(shù)值可知，定義河道堤防的水位數(shù)值在成災(zāi)水位的3/4時，則定義該測點處于不安全狀態(tài)。分別使用文獻[2]中的安全評價方法、文獻[6]中的安全評估方法以及文中設(shè)計的安全評估方法進行實驗，對比3種安全評估方法的性能。

2.2 結(jié)果及分析

基于上述實驗準備，設(shè)定上述3種安全評估方法作用表2中的測試點，控制上述測試點在相同的季節(jié)內(nèi)，保證測點不受外部環(huán)境的影響。使用3種安全評估方法模擬計算測點處的水深，以人工測量的水深數(shù)值作為對比，3種安全評估方法最終得到的測點水深數(shù)值及誤差見表3。

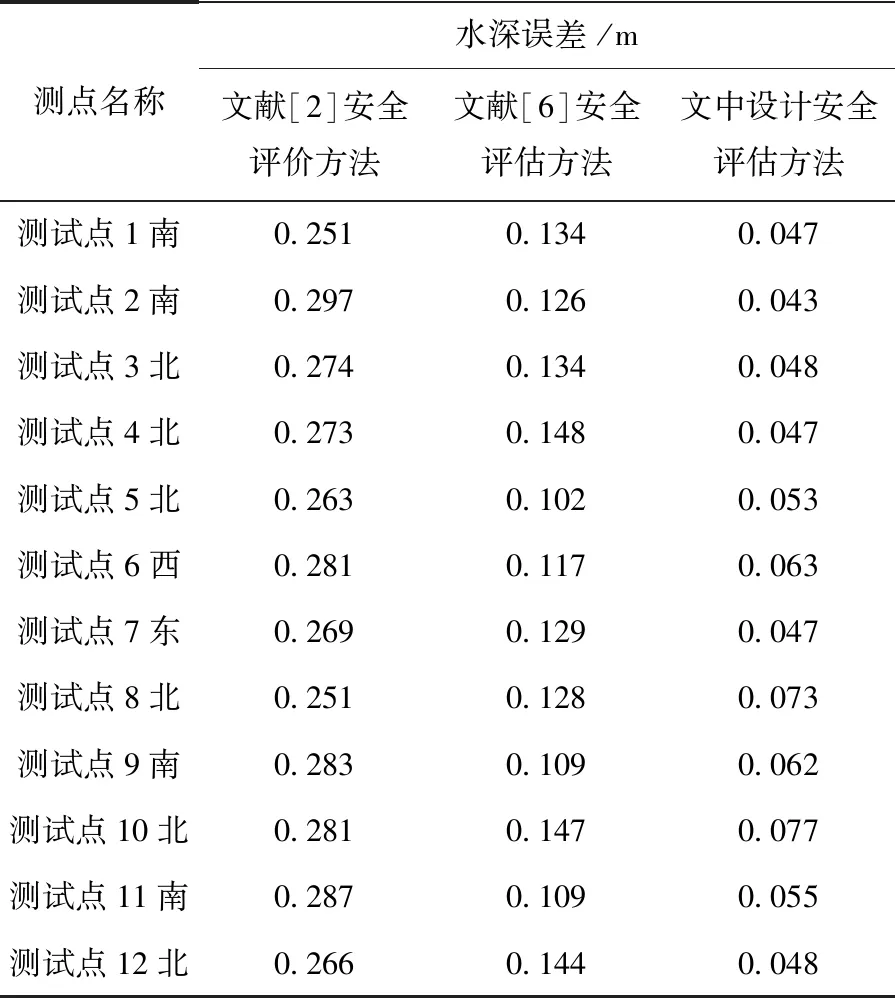
表3 3種安全評估方法評估水深誤差

由表3誤差結(jié)果可知，以實際測量的測量點的水深數(shù)值作為標準數(shù)值，根據(jù)測量結(jié)果可知，文獻[2]中的安全評估方法得到的平均水深誤差數(shù)值在0.273 m，水深數(shù)值最大；文獻[6]中的安全評估方法得到的平均水深數(shù)值在0.127 m左右，得到的水深數(shù)值誤差較小；而文中設(shè)計的安全評估方法得到的平均水深數(shù)值在0.055 m左右。與上述兩種文獻中的安全評估方法得到的水深誤差數(shù)值相比，文中設(shè)計方法得到的水深誤差數(shù)值最小。

保持上述實驗環(huán)境不變，匯總3種安全評估方法評估過程使用的指標，以該指標作為實驗對象，聯(lián)合安全評估方法得到的模擬值，構(gòu)建評估指標的精度檢驗計算公式，可表示為：

(10)

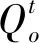
控制3種安全評估模擬處理相同時間段的水深數(shù)據(jù)，3種安全評估方法的精度結(jié)果見圖3。

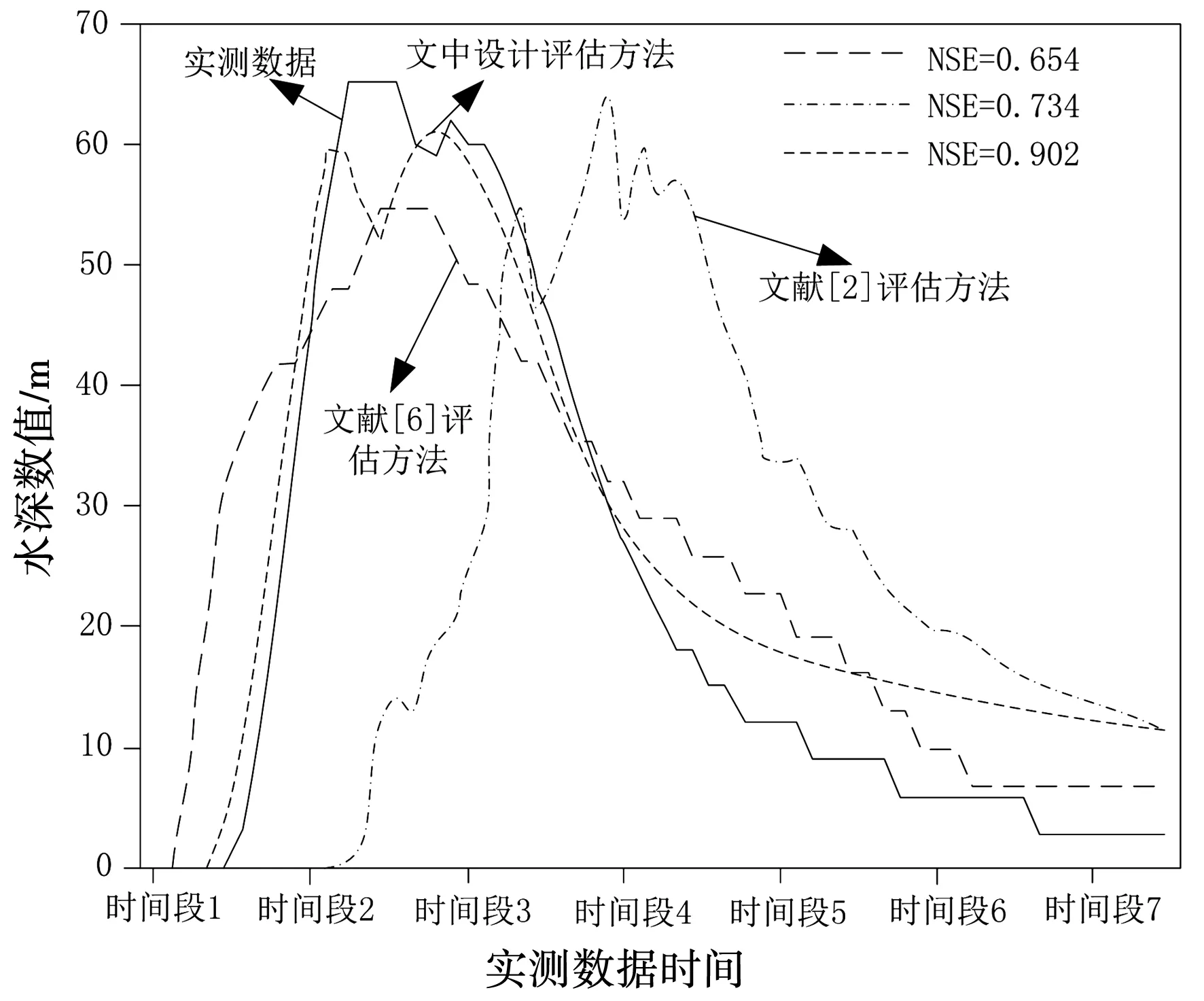
圖3 3種安全評估方法精度結(jié)果

由圖3所示的指標精度結(jié)果可知，以相同時間段內(nèi)的實測數(shù)據(jù)作為處理對象，根據(jù)圖3中數(shù)值結(jié)果可知，文獻[2]中的安全評估方法的平均NSE數(shù)值為0.654，精度數(shù)值較小；文獻[6]中的安全評估方法的平均NSE數(shù)值在0.734左右，評估方法涉及處理的指標精度較高；文中設(shè)計的安全評估方法平均的NSE數(shù)值在0.902左右。與上述兩種文獻中的安全評估方法相比，文中設(shè)計的安全評價方法實際評估過程指標的精度數(shù)值最高。

在上述實驗環(huán)境下，整理3種安全評估方法的評估指標，計算各個指標的特征變量，計算公式為：

(11)

其中：pt為特征變量的集合。

根據(jù)上述計算公式得到的數(shù)值結(jié)果，使用邊際分布worm圖處理特征變量數(shù)值，以變量數(shù)值的單位正態(tài)殘差作為標準，3種安全評估方法得到特征變量的擬合優(yōu)度結(jié)果見圖4。

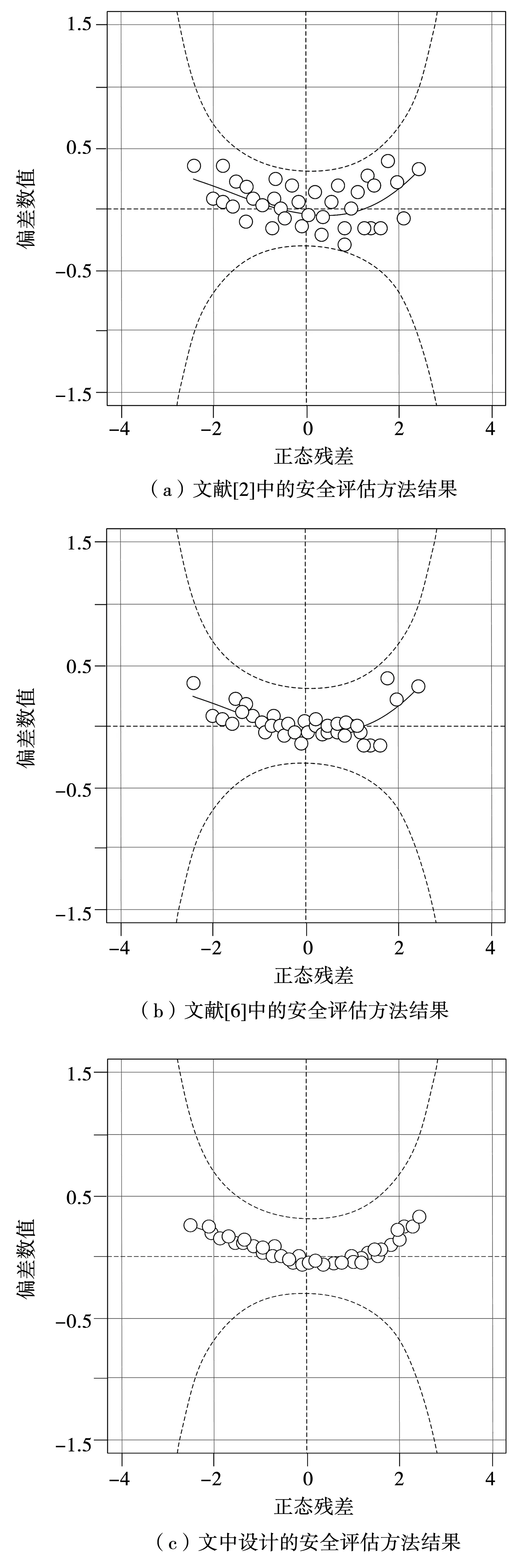
圖4 3種安全評估方法結(jié)果

由圖4所示的實驗結(jié)果可知，控制3種安全評估方法的正態(tài)殘差為固定區(qū)間，根據(jù)圖4中散點的分布情況可知，文獻[2]中的安全評估方法散落在置信線的兩側(cè)，該種方法指標的頻率并未存在足夠的擬合優(yōu)度；文獻[6]中的優(yōu)化方法的散點分布較為緊湊，該種方法指標頻率存在較強的擬合優(yōu)度；而文中設(shè)計的評估方法對應(yīng)得到的散點較為緊湊，安全評估指標的擬合優(yōu)度較強。

3 結(jié) 語

城市洪澇災(zāi)害不斷增多，如何安全評估城市河道堤防的安全狀態(tài)成為當下的研究重點。在水動力模型的支持下，設(shè)計一種安全評估方法，能夠改善現(xiàn)有安全評估方法指標精度數(shù)值過小、預(yù)測河道水深數(shù)值不準確、安全評估指標擬合優(yōu)度較弱的問題。但文中設(shè)計的安全評估方法使用的水動力模型參數(shù)屬于固定數(shù)值，對不同城市條件下的河道堤防是否適用還有待研究，對河堤的安全評估工作還需不斷地學(xué)習(xí)研究。