開溝鋪管機高程主控臂輕量化設計

楊一男，姚 強，耿冠杰，張 鑫，莊 重，李 怡

(1.中國農業機械化科學研究院，北京 100083；2.北京天順長城液壓科技有限公司，北京 100083)

0 引言

農田暗管排水控鹽技術利用人為埋入地下的孔管，排出土壤中多余水分與鹽漬，達到改善土壤理化性狀的目的。迄今，大量實踐應用證明，該技術不僅可以改善土地質量，保持地力，還可以增加農業產量，提高農業經濟，防止環境退化[1-4]。目前，開溝鋪管是技術實施的主要方法，使用以開溝鋪管機為核心的施工裝備，實現農田暗管系統的全機械化施工，是農田暗管排水控鹽技術大規模應用的根本出路。

開溝鋪管機融合機、光、電、液等多學科技術，實現集開溝、鋪管、敷料和質量控制為一體的集約化施工。機械結構設計的合理性是保證機器各項功能完美實現的基礎，也是評價整機性能與成熟度的重要指標。但是，國內外關于大型鋪管機研發的公開資料很少，針對其關鍵部件優化設計的研究更為少見[5-9]。

為此，本文基于TC3050HT型大功率開溝鋪管機，采用有限元方法，對機器的高程主控臂開展靜力學和瞬態動力學分析，并以分析結果為依據，對高程主控臂的結構進行優化改進，實現結構輕量化，達到提高設計合理性的目的，以期能為今后同類機器高程主控臂的優化設計提供參考。

1 結構原理

TC3050HT型鋪管機發動機額定功率310 kW，通常開溝寬度220～280 mm，鋪管深度2.5 m，作業速度1 km/h左右，該機器作業時的狀態如圖1所示。

圖1 TC3050HT型開溝鋪管機

該機執行機構的結構原理如圖2所示。其中，開溝鋪管機的高程主控臂連接機架與開溝臂，作業時在高程控制油缸的驅動下，通過改變高程主控臂的角度，實現高程控制，此外高程控制臂上方還安裝有開溝臂控制油缸。因此，高程主控臂是執行機構中承載和傳力的關鍵部件，其結構強度決定整機運行可靠性，質量大小影響高程控制響應速度。

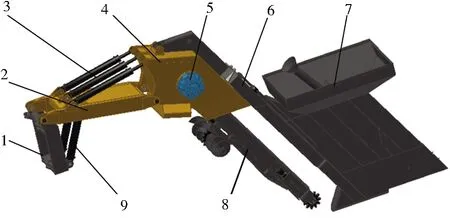
1.支座(與機架相連) 2.高程主控臂 3.開溝臂控制油缸 4.開溝罩 5.液壓馬達 6.管箱臂 7.管箱 8.開溝臂 9.高程控制油缸

高程主控臂(圖3)由方形管材框架和擋板構成，在位置1與開溝罩鉸接，在位置2與角度控制油缸鉸接，在位置3與支座鉸接，在位置4與高程控制油缸鉸接。

圖3 高程主控臂

2 高程主控臂有限元分析

為更接近高程主控臂工作的實際情況，完整反映其力學特性，對包含高程主控臂在內的執行機構整體進行剛柔耦合分析。

2.1 靜力學分析

采用四面體網格劃分高程主控臂，網格質量符合GB/T 33582—2017《機械產品結構有限元力學分析通用規則》推薦要求[10]。假設除高程主控臂外的結構均為剛體。所有零件材料均為結構鋼，密度7.85×103kg/m3，彈性模量210 MPa，泊松比0.3。

高程主控臂與周圍零部件均采用轉動副連接。油缸筒與各自活塞桿均采用滑動副連接。角度控制油缸與高程控制油缸均為驅動油缸，選擇驅動位移作為變量，靜力學分析時，設置位移為零。

靜力學分析載荷邊界如圖4所示。使用mass21單元，等效液壓馬達的質量；依據施工經驗，在開溝臂上施加水平方向26.8 kN的極限均布載荷；在管箱內壁施加16.5 kN的均布載荷，模擬砂礫濾料的作用力；對模型整體施加豎直向下的重力加速度。

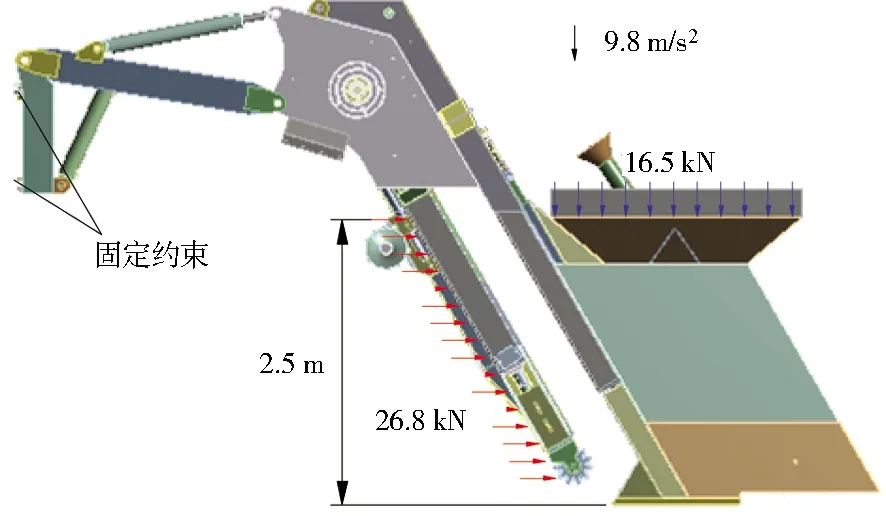
圖4 靜力學分析載荷邊界

靜力學計算結果如圖5所示。其中，高程主控臂框架的最大應力44.67 MPa，結構最大變形量1.26 mm。框架采用Q235方管材料，最大許用應力235 MPa，所以抗失穩系數>5。

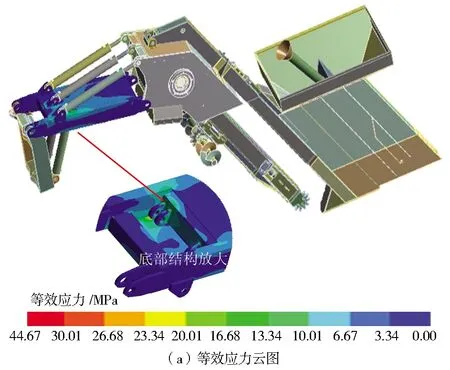
圖5 靜力學計算結果

2.2 瞬態動力學分析

為避免有限元算法振蕩導致的結構受力波動，對角度控制油缸與高程控制油缸分別施加3個周期的位移驅動，如圖6所示。考慮3個周期對迭代收斂性的影響，初始載荷子步為75，最小載荷子步為60，最大載荷子步為750。載荷增量為每0.1 s增加2 mm位移。打開大變形開關。其他設置與靜力學模塊相同。為保證計算結果的準確性，以算法穩定的第3周期結果作為參考。

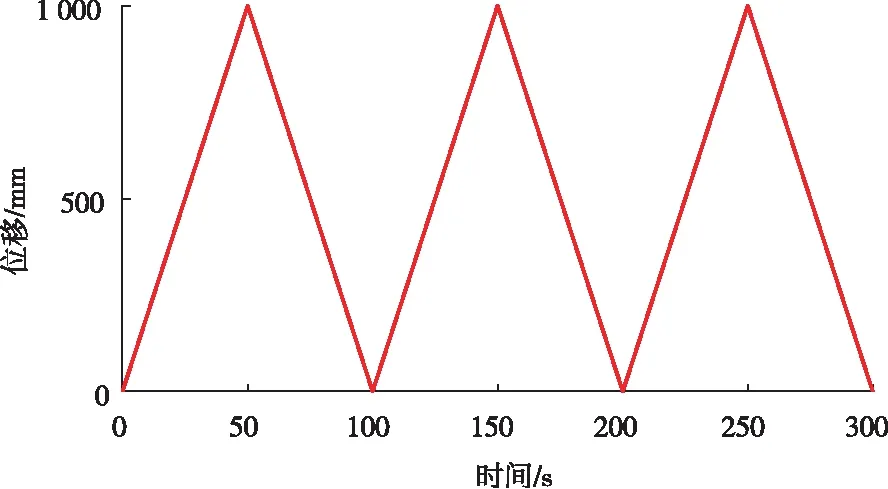
圖6 驅動位移曲線

瞬態分析過程中應力最大時刻的等效應力云圖如圖7所示，其中連接橫梁的最大等效應力50 MPa，抗失穩系數約為5。

圖7 瞬態分析等效應力云圖

3 優化分析

通過靜力學與動力學分析可知，高程主控臂的結構抗失穩系數約為5，結合實際工程設計經驗，對于沒有特殊要求的結構件，在兼顧合理與經濟性的前提下，結構抗失穩系數合理范圍為2.5～3.0，所以該結構存在優化空間。并且考慮實際型材的二次加工會增加額外成本，本研究主要針對型材厚度進行優化。

3.1 靜力學分析與瞬態動力學分析

對高程主控臂進行精細化網格劃分，如圖8所示。其中，采用2D四邊形單元劃分板材、管材等薄壁件，主體結構各部分采用共節點的連接方式，采用剛性單元RB2模擬連接位置與控制臂主體間的焊點。通過靜力學方法進行求解，載荷工況如表1所示。其中，工況1載荷與前述靜力學分析中的載荷等效，是高程調節油缸沒有位移輸出時的極限工況；工況2和3是在工況1的基礎上，高程調節油缸輸出位移，但發生結構鎖死，導致上下油缸無法推動的工況，其中油缸的極限推力為60 kN。

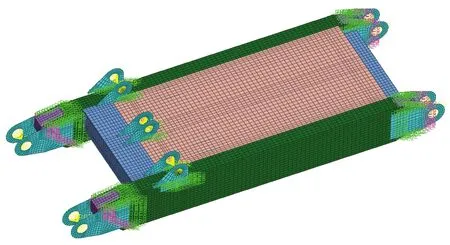
圖8 高程主控臂網格劃分

表1 載荷工況

3.2 工作執行裝置的尺寸優化分析

優化變量為高程主控臂的縱梁與橫梁的壁厚，初始壁厚(圖9)分別為12和10 mm。

圖9 高程主控臂框架

優化過程中的響應包括體積響應、應力響應和位移響應。約束條件為應力約束和變形約束，即抗失穩系數為3，各工況的應力上限為80 MPa，變形不超過原結構變形的1.5倍(表2)。優化目標為最小化體積。

表2 約束條件

設計變量和位移響應的迭代曲線分別如圖10～11所示，經過3次迭代計算，得到厚度優化結果和約束條件下的變形結果。

圖10 設計變量迭代曲線

圖11 最大位移迭代曲線

高程主控臂優化后網格厚度如圖12所示，計算得到縱梁與橫梁壁厚分別為8.76和8.22 mm，均向上圓整，實際選取縱梁與橫梁的壁厚為9 mm。縱梁與橫梁的優化前后受力分析結果對比如表3～4所示。

圖12 高程主控臂優化后網格厚度

由表3～4可知，由于管材壁厚減小，優化后各工況下的最大應力和最大位移均有所增長，但結構抗失穩系數在2.5～3.0的合理范圍內，因此優化后的高程主控臂結構設計合理。

表3 縱梁優化效果

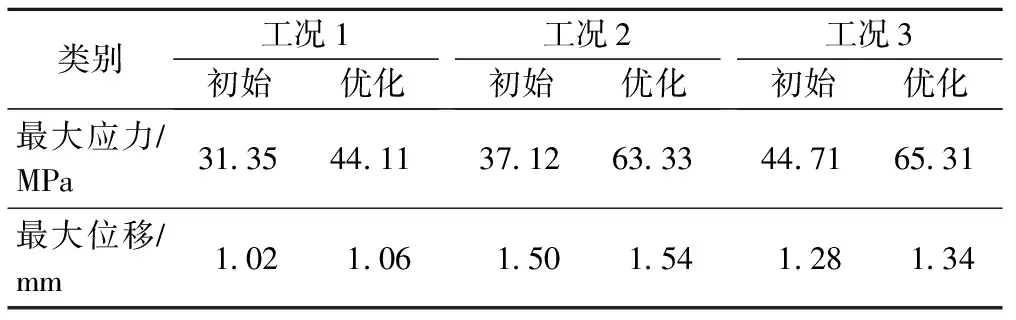
表4 橫梁優化效果

4 結論

針對開溝鋪管機執行機構，開展基于有限單元法的靜力學與瞬態動力學剛柔耦合分析。結果表明，高程主控臂強度抗失穩系數高于許用抗失穩系數，剛性變形量處于微變形階段，屬于材料的線性變形區。結構強度和穩定性遠高于實際工況的使用需求，滿足結構輕量化設計的前置條件。

基于最優化準則，在保證高程主控臂可靠性的前提下，通過將單元厚度離散化迭代，并采用逐步逼近的算法，得到框架結構的最優厚度9 mm。與原結構相比，優化后的結構單元厚度減小，力學性能和剛性雖略有降低，但抗失穩系數仍滿足要求。因此，優化后的高程主控臂結構設計合理。

研究內容能夠為今后同類機器高程主控臂的設計提供參考，研究方法為開溝鋪管機的輕量化設計提供了一種技術途徑。