基于SSA-LSTM的鋰離子電池壽命預測 ①

郭 玄，朱 凱

(江蘇理工學院汽車與交通工程學院，江蘇 常州 213001)

1 前言

電池健康狀態(State of Health，簡稱SOH)表征了電池的容量衰減程度和當前可用容量，對SOH的估計不準確將直接影響電池荷電狀態(State of Charge，簡稱SOC)估算，導致用戶對電池狀態的錯誤判斷。國內外對SOH有多種定義，主要有：容量、電量、內阻、循環次數和峰值功率等。電池健康狀態從電池使用、維護以及經濟性表明了在工業應用方面的重要意義，因此研究SOH有利于掌握電池老化因素幫助判斷電池的內在隱患和壽命情況。預測SOH的主流方法是數據驅動方法，其不像物理模型方法具備一定物理知識研究，僅需大量數據，通過學習數據內在規律即可描述電池內部的反應[1-3]。然而數據驅動方法存在模型單一或者其模型參數調整難等問題，學者采用優化算法彌補其預測模型的缺陷。目前，針對優化鋰電池SOH預測方法的智能算法主要有人工蜂群算法[4]、螢火蟲算法[5]、遺傳算法[6]、粒子群優化算法[7]等。Karaboga等模擬蜜蜂采蜜原理，以觀察蜂、偵查蜂和采蜜蜂之間條件轉換，每個蜜源代表一個待求解，因此對算法影響最大的因素為蜜源的開采次數限制，開發力度影響蜜蜂的搜索力度和跳出局部最優的能力[4]。Goldberg等通過模擬自然生物的遺傳、進化適應環境變化的特點進行交叉、變異和選擇三種操作對參數尋優，但是缺點是求解速度慢，存在局部最小問題[6]。Seyedali等模擬鯨魚捕食，以包圍獵物和氣泡網圍捕方法具有良好的泛化能力，但缺點是和螢火蟲算法相似，前期進行全局搜索，后期進行局部搜索，沒有跳出局部最優的操作，從而對復雜問題性能有所下降[8]。He等基于發現者、游蕩者、跟隨者模型產生的算法，游蕩者起到跳出局部最優作用，跟隨者作用為局部搜索，發現者引導跟隨者，但發現者貢獻不多并使得算法實現更復雜[9]。

相比上述多種優化算法，新進算法中的麻雀搜索算法在收斂速度和尋優精度等方面有著明顯優勢并且結構簡單、能準確應對復雜問題[10]。所以針對鋰電池長序列數據依賴關系問題，提出SSA-LSTM模型(Sparrow Search Algorithm-Long-Short Term Memory，簡稱SSA-LSTM)，其中長短期記憶神經網絡模型(Long-Short Term Memory，簡稱LSTM)[11]，對長序列數據不僅具備更好的傳遞記憶功能，并且能消除反向梯度消失問題，而在預測過程中長短期記憶神經網絡模型出現超參數調整困難、收斂速度慢等情況，提出與麻雀搜索算法相結合，形成SSA-LSTM模型，優化LSTM超參數，減小超參數調整困難、收斂速度慢等問題的影響。

2 LSTM長短期記憶神經網絡

如圖1所示，LSTM是根據循環神經網絡(Recurrent Neural Network，簡稱RNN)改進得來，消除RNN網絡的反向傳播梯度消失問題，可以保留長短序列依賴關系。LSTM通過遺忘、輸入、輸出三個結合激勵函數，統稱為“門”的結構來去除或者增加信息到單元狀態。有sigmoid函數將輸出0-1之間的數字，代表信息應該通過多少。值為0表示不讓任何信息通過，而值為1表示讓所有的信息通過，通過這三個門保存和控制單元狀態。

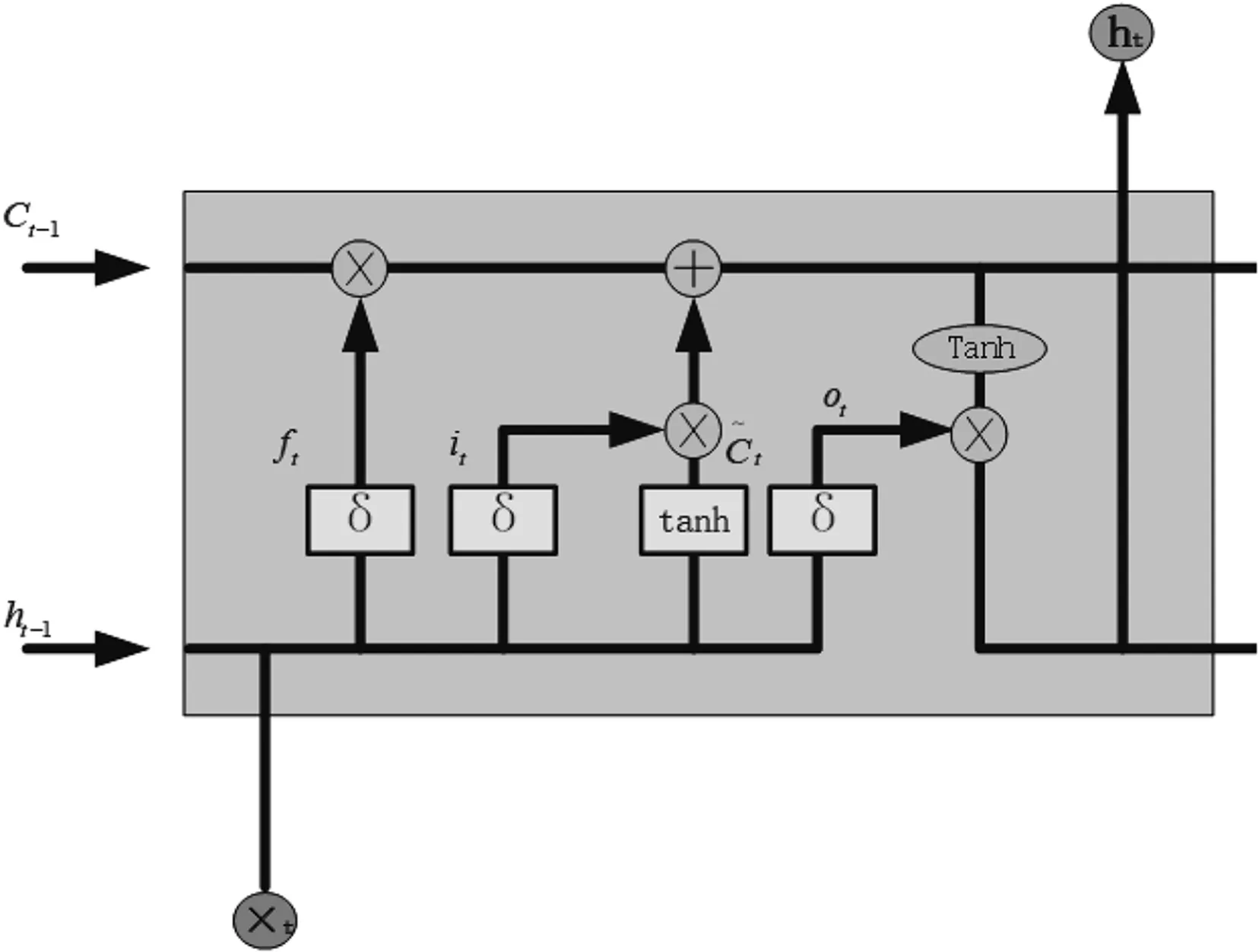
圖1 LSTM單元Fig.1 LSTM unit.

遺忘層：決定從單元狀態中去除哪些信息。其計算公式為：

ft=σ(Wf[ht-1,xt]+bf)

(1)

輸出層：同時輸出單元狀態和隱藏狀態給下一層。其計算公式為：

it=σ(Wi[ht-1,xt]+bi)

(2)

(3)

輸入層：將舊的單元狀態更新為新的單元狀態，其計算公式為：

(4)

ot=σ(Wo[ht-1,xt]+bo)

(5)

ht=ot*tanh(Ct)

(6)

其中，ht-1表示為上一單元隱藏層輸出，xt表示當前單元輸入，Wf和bf分別表示該門的權重和偏置量。

3 麻雀搜索算法

麻雀搜索算法(Sparrow Search Algorithm，簡稱SSA)是根據麻雀覓食并躲避追捕者的行為提出的一種群智能優化算法，麻雀種群分發現者和跟隨者，搜索到較好食物的麻雀為發現者，其余為跟隨者，種群中選取一定比例的麻雀帶有偵察預警機制的行為動作，發現危險及時放棄食物。麻雀不斷搜索更好食物過程即為解的尋優過程。假設麻雀種群數量為N，每代選取種群中位置最好的PN只麻雀作為發現者，N-PN只麻雀作為跟隨者，搜索的空間為D維，麻雀的i(i∈1,2,…,n)位置為xi=(xi,1,xi,2,…,xi,D)，麻雀種群最優位置為xb=(xb,1,xb,2,…,xb,D)，在t+1次迭代中，其發現者位置更新為：

(7)

i,j表示第i個麻雀在第j維中的位置信息，itermax表示為最大迭代次數，Q表示為正態分布隨機數，L表示為1×d矩陣且其元素均為1。

其追隨者位置更新為：

(8)

xworst表示當前全局最差位置，xp表示目前發現者占據的最優位置，表示1×d矩陣，其每個元素隨機賦值1或-1，且A+=AT(AAT)-1。

在實驗中，假設帶有偵察預警機制行為動作的麻雀占總數量的10%-20%，這部分麻雀初始位置在種群中的位置為隨機產生，其位置公式為：

(9)

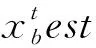
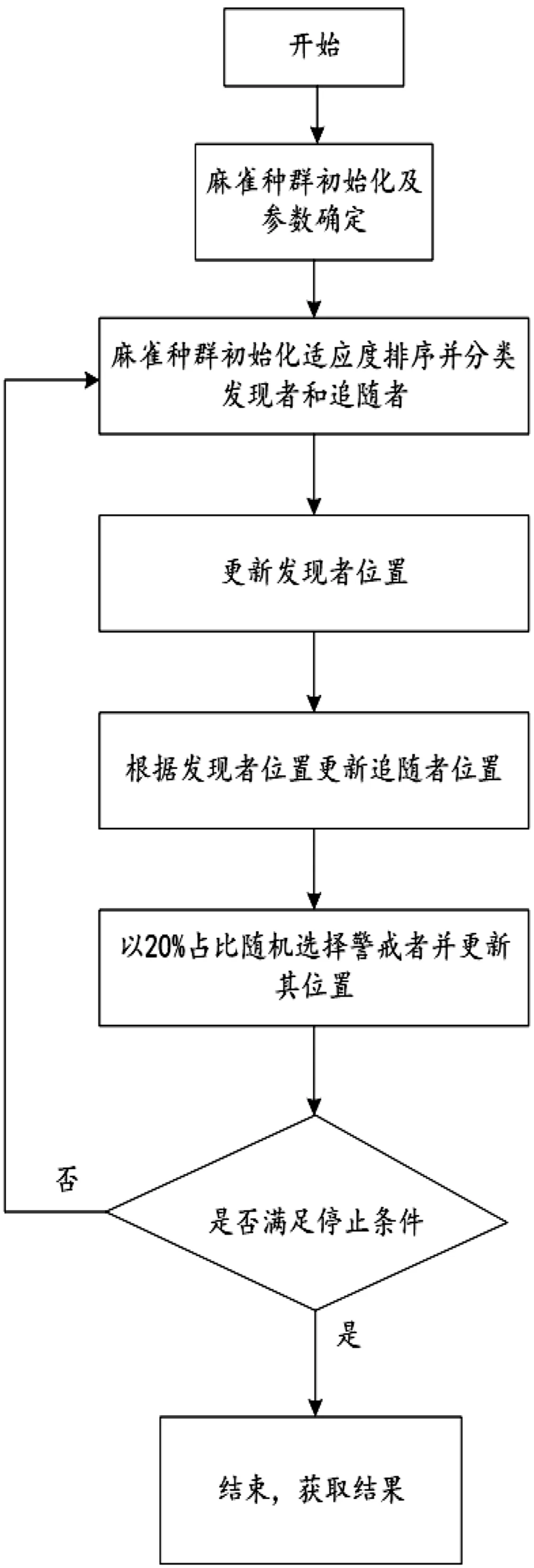
圖2 SSA算法流程圖Fig.2 SSA algorithm flowchart.

4 SSA-LSTM模型

在LSTM中一般學習率、迭代次數、神經元個數等超參數對預測結果的準確性影響較大，因此將LSTM中的三個參數作為SSA的優化變量，提出SSA-LSTM算法，具體步驟如下：

將每次放電后的電池容量以及對應放電次數數據提取作為預測數據集，為加快最優解求解速度和提高精度，采用簡單縮放即min-max標準化方法對數據進行歸一化。歸一化公式如下：

(10)

其中，x為樣本數據，min和max分別表示為樣本數據中最小值和最大值，Xnew表示歸一化處理后的數據，通過min-max歸一化方式對樣本數據進行線性變換，結果落于[0,1]區間。

在尋優搜索算法中，確定麻雀種群數量，根據超參數組個數確定麻雀位置loc尋優維度，確定發現者麻雀所占種群比例，一般選取20%。

確定超參數上下邊界，初始化麻雀位置loc,loc由尋優超參數組組成。初始化參數包括麻雀最佳位置bestX，全局最佳適應度fMin，最佳適應度pFit等。

將初始化的麻雀位置根據適應度函數評估麻雀位置并進行排序，取前20%為發現者，余者為跟隨者，隨機選取10%-20%的麻雀攜帶偵察預警機制動作。

通過發現者、追隨者以及預警條件公式更新麻雀位置，接著以邊界函數約束超參數并對LSTM所需超參數傳參進行預測，返回結果通過適應度函數進行評估位置。若當前麻雀位置適應度優于最佳位置的麻雀適應度則代替，否則不變。若本次迭代中麻雀最佳適應度優于全局最佳適應度則代替，否則不變。

判斷是否滿足設定的達到誤差和最大迭代次數的停止條件。若符合，則將全局最優超參數組設為LSTM的參數；若不符合，則返回4。

具體步驟如圖3所示：

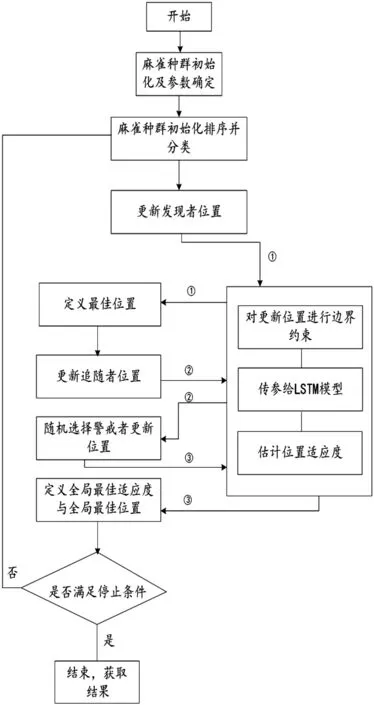
圖3 SSA-LSTM算法流程圖Fig.3 The flowchart of the SSA-LSTM algorithm.

5 實驗結果及分析

5.1 數據獲取

本實驗所用數據來自美國NASA航天局[12]。在鋰電池充放電實驗中充電截止電壓為4.2 V，放電截止電壓為2.7 V。數據通過實驗方式獲取，鋰離子電池5號在室溫下通過3種不同的操作模式測量：

充電模式：通過1.5 A恒流充電至4.2 V電壓水平并且涓流電流為20 mA時停止充電。

放電模式：通過2 A恒流放電至2.7 V電壓水平時停止放電。

內阻模式：通過阻抗譜對[0.1,5000]區間頻率掃描進行測試。

在實驗過程中，通過對電池老化的影響操作并記錄電池的放電容量、循環次數、內阻以及溫度。隨機從數據中選取30%的數據作為測試集，其余作為訓練集。輸入變量為循環次數、放電電池溫度、電池內阻，輸出變量為可用容量。

5.2 結果分析

本實驗中，麻雀搜索算法參數定義：麻雀種群數量為10，尋優維度為3，麻雀生產者的比例為0.2，搜索算法迭代次數為40，麻雀位置初始化范圍(LSTM超參數初始化)分別為：學習率[0.001,0.01]，迭代次數[1,100]，神經元個數[1,100]，LSTM模型由單層LSTM單元組成。對比算法Single-LSTM超參數定義：迭代次數20，學習率0.001，神經元個數100，批次大小16。在獲取實驗數據并進行預處理后，分別用BP、LSTM、SSA-LSTM算法進行實驗對比，圖4～6以及子圖分別為上述模型的預測對比圖，表1為各模型的預測結果比較。

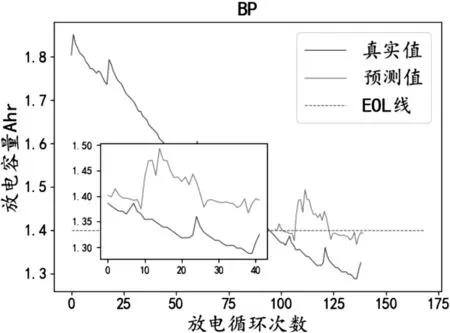
圖4 BP預測結果Fig.4 BP prediction result.

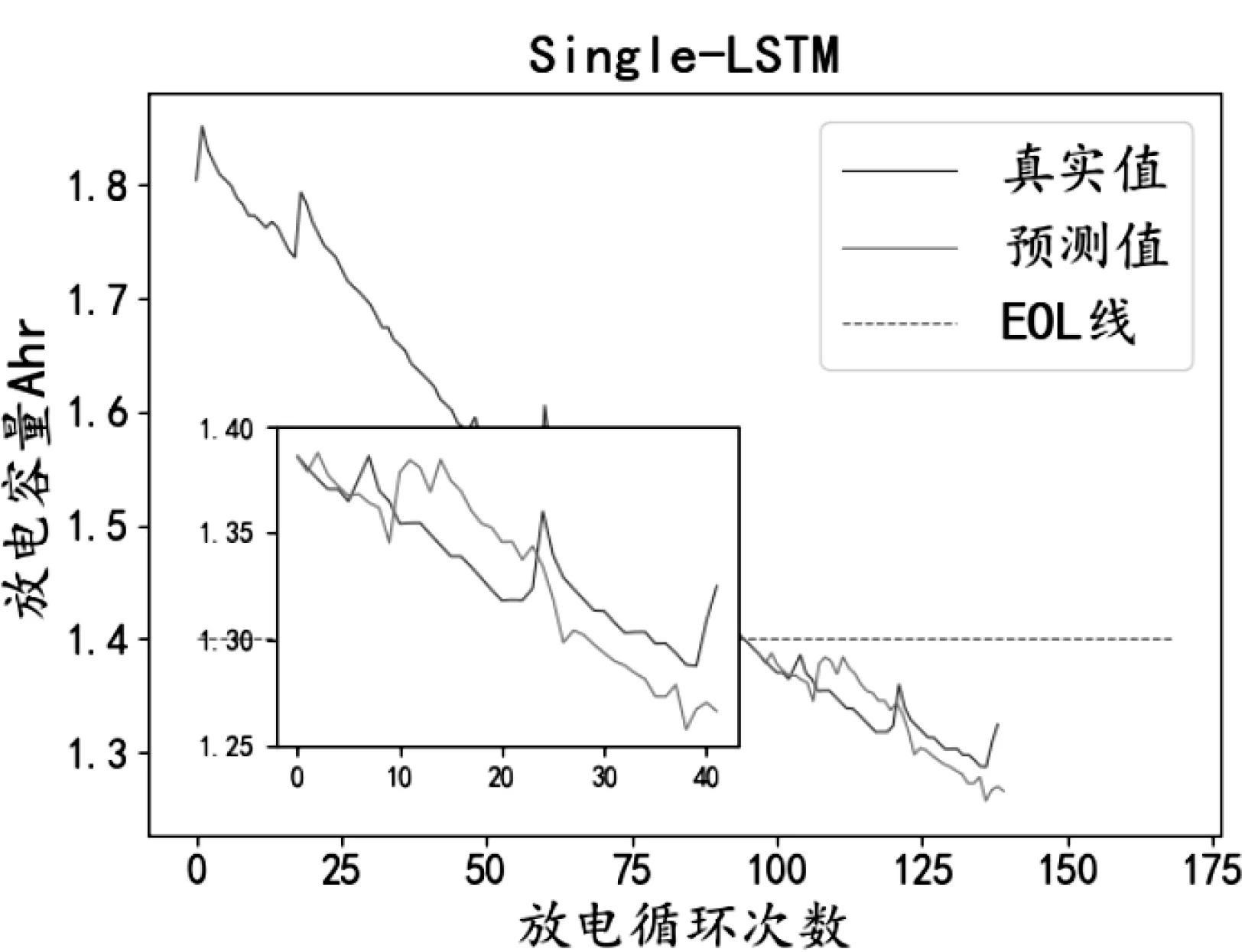
圖5 單純LSTM預測結果Fig.5 Single LSTM prediction result.

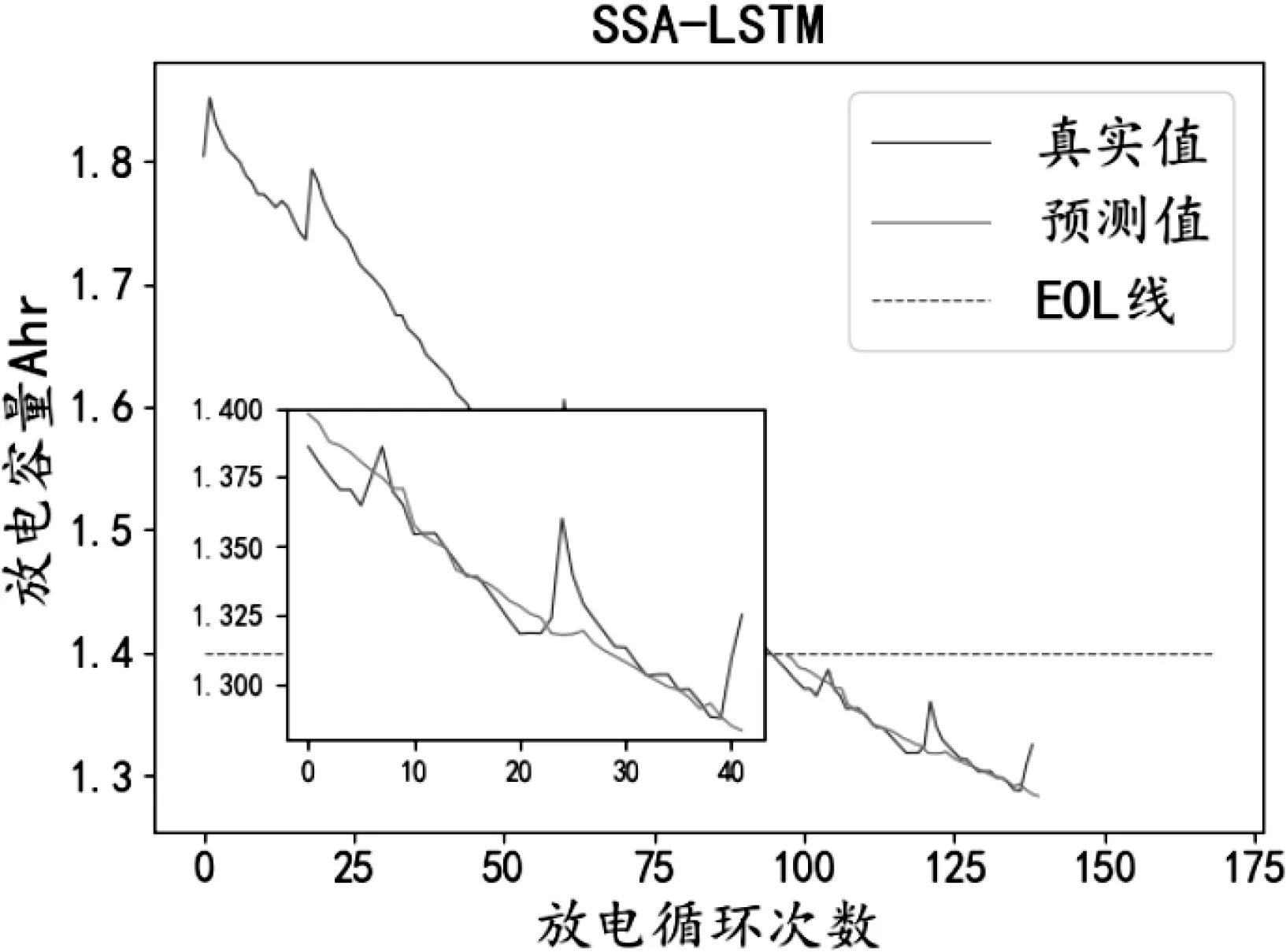
圖6 SSA-LSTM預測結果Fig.6 SSA-LSTM prediction result.

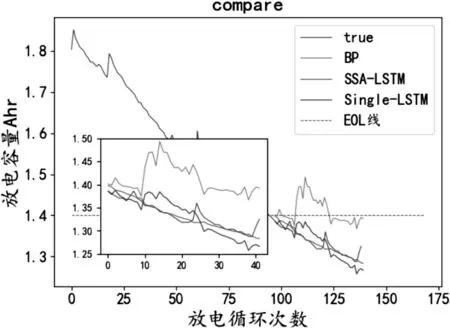
圖7 各模型預測結果Fig.7 Prediction results of various models.

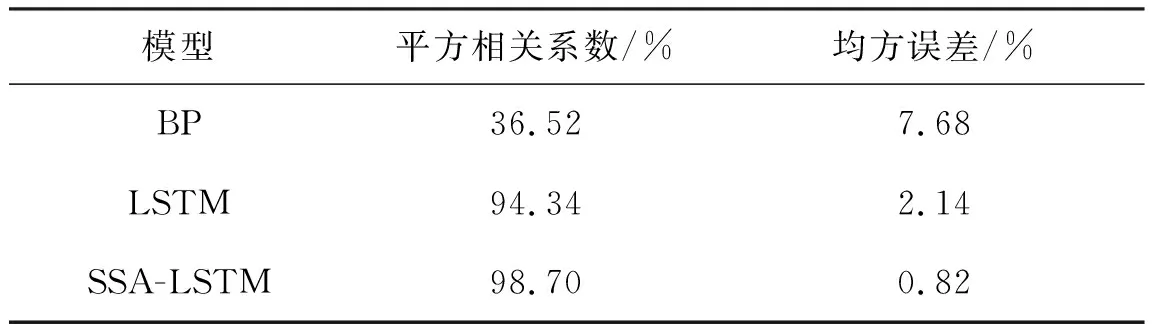
表1 各模型預測結果比較Table 1 Comparison of prediction results of various models.

從圖4-5和表1中可以看出相對于BP算法，LSTM算法的均方誤差和平方相關系數優化了5.54%、57.82%，證明了LSTM長序列預測性能效果。從圖5-6和表1中可以看出SSA-LSTM模型的均方誤差和平方相關系數相比LSTM算法在平方相關系數提高了4.36%，在均方誤差方面降低了1.32%。并且SSA-LSTM算法通過圖6可以看出與真實值擬合良好，說明SSA算法對于優化LSTM超參數具有較好的效果，從而驗證了SSA算法的有效性。

6 總結

SSA算法具有較快的收斂速度和強大的搜索能力，采用網格搜索或者枚舉搜索等方法對LSTM參數進行尋優時，即耗時較長、精確度也并不高，因此本文利用SSA來優化LSTM的超參數并形成了SSA-LSTM模型。通過Python工具對數據集進行對比試驗分析證明：SSA-LSTM模型具有較好的學習能力，是一種有效的LSTM超參數尋優算法。SSA麻雀搜索算法作為目前的新晉算法，因其收斂速度過快和麻雀跳躍式更新方式使其容易陷入局部最優，所以接下來的工作可以從如何跳出局部最優以及麻雀位置更新方式著手。