高速動車組齒輪箱模態分析及優化設計

高 揚 方翁武 魏昱洲 趙 慧

(中車戚墅堰機車車輛工藝研究所有限公司 江蘇 常州 213000)

0 引言

隨著我國高速鐵路的快速發展，列車運營時速已至350 km/h，高速的運行使得車輛各部件的工作環境愈加復雜。齒輪箱驅動裝置作為保證高速動車組持續穩定運行的關鍵零部件，其運行的可靠性、穩定性、安全性將直接影響傳動系統甚至動力車整車的正常運行[1]。

高速動車組齒輪箱在內外激勵的作用下會產生振動，當齒輪箱的低階固有頻率與工作頻率接近時系統產生共振，嚴重的共振會加速零部件的損壞，降低齒輪箱使用壽命[2]。開展高速動車組齒輪箱模態分析，識別齒輪箱的模態參數，包括固有頻率、振型、剛度等，不僅可為結構動力特性的優化設計提供依據，還可用于故障診斷及預報，對于保障高速動車組的正常線路運營具有重要意義。本文以國內典型高速動車組齒輪箱箱體為研究對象，運用振動理論、有限元方法和模態測試手段開展了齒輪箱的振動特性研究，獲得箱體的固有頻率和模態振型，通過對仿真結果和試驗結果的對比分析，確認了不同結構類型箱體對模態特性的影響，提出優化提升設計建議，并驗證其正確性。

1 模態分析理論基礎

模態是表征自由振動時結構振動特性的量，由系統本身的屬性和材料特性決定，與外部載荷無關。對系統進行模態分析，可得到系統的固有頻率以及在固有頻率下的固有振型，低階固有頻率對系統的振動特性有著重要的影響[3]。

對于一個自由度的線性振動系統，其運動微分方程的一般表達式為：

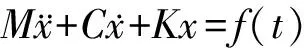
(1)

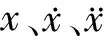
經拉氏變換得：

(s2M+sC+K)X(s)=F(s)

(2)

在傅氏域內處理，用jω代替s得：

(K-Mω2+jωC)X(ω)=F(ω)

(3)

對于線性系統，各階模態響應的線性疊加組成了結構的響應：

Xi(ω)=φi1q1(ω)+φi2q2(ω)+…φirqr(ω)

(4)

其中：qr(ω)為r階模態坐標，φir測點r階模態振型參數。

可視為自由振動的系統，其運動微分方程為：

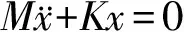
(5)

變換到模態坐標為：

(K-ω2M){φ}=0

(6)

2 模態有限元仿真

針對國內典型時速350 km高速動車組齒輪箱進行模態的分析研究，A和B為兩種不同結構的齒輪傳動系統，其中A型傳動系統箱體為整體式，B型傳動系統箱體為分體式，兩種結構齒輪傳動系統的外部接口參數、輸入工況、箱體選用材料均相同，整體質量相差小于3%，其結構如圖1所示。

(a)A型齒輪傳動系統 (b)B型齒輪傳動系統圖1 時速350 km高速動車組齒輪傳動系統

在Cero中建立箱體三維模型，導入有限元分析軟件中。齒輪箱箱體的材料為鋁合金，彈性模量為7.5×1010Pa，密度為2 770 kg/m3，泊松比為0.3[4]，計算箱體自由模態，對箱體模型不施加任何邊界條件[5]。箱體模型采用四面體二次單元進行網格劃分，計算后得到前10階模態如表1所示。

前十階模態中，A型齒輪箱各階模態均低于B型齒輪箱，其原因在于A型齒輪箱為整體結構，整體結構簡單，為提升其鑄造工藝性，箱體內外表面圓滑過渡，過渡曲面圓潤，而B型齒輪箱為分體箱，整體結構相對復雜，上下箱體分別澆鑄，箱體內外表面增設了較多的加強筋和集油筋板，曲面過渡棱角分明，箱體與輸出端法蘭不再采用垂直連接的形式，而是設計一定的傾角，改變了箱體的質量分布，局部提升了箱體剛度，較整體箱而言不易被激振出現共振現象。

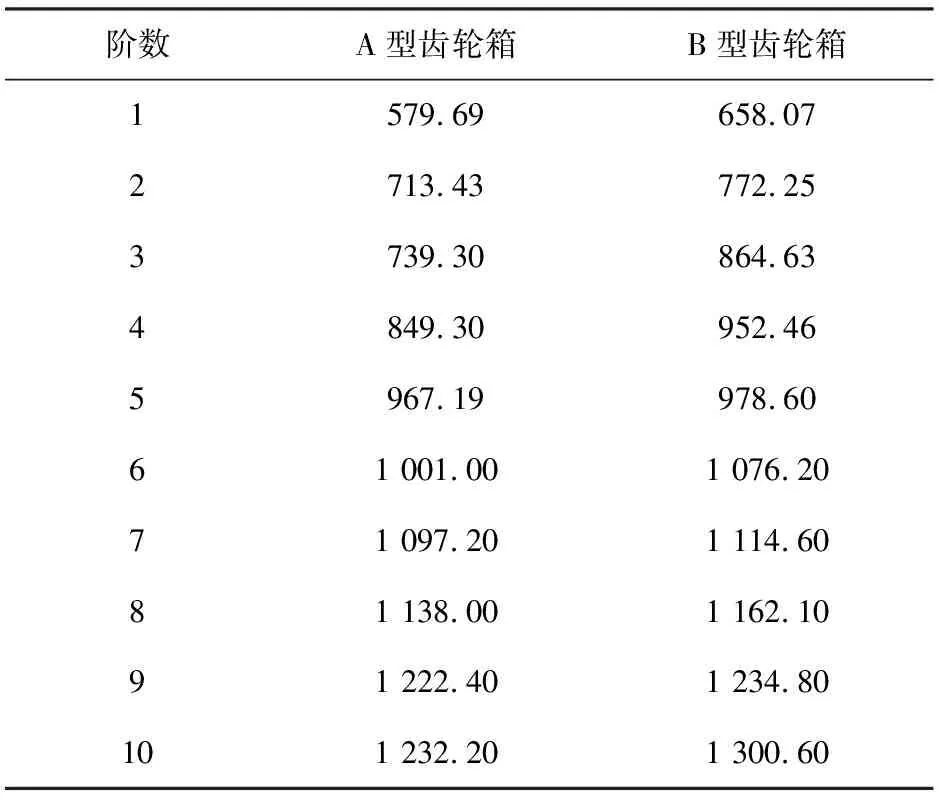
表1 齒輪箱前10階自由模態頻率 /Hz

分析兩種齒輪箱的模態振型可知，齒輪箱在共振頻率下，不僅存在三個方向的擺動，還有扭轉振動和彎曲，有局部振動變形，也有整體式呼吸變形，均屬于復雜的復合振動，且兩種結構的箱體在前端吊掛區域和大小法蘭連接區域的振動形變均較大。這些振動在影響箱體結構本身的強度和壽命的同時，也影響傳動系統內部零件的正常工作狀態，因此在設計過程中需合理布置齒輪箱結構，在保證輕量化的基礎上提升箱體整體或局部剛度，以達到減小和抑制振動的目的。

3 箱體結構優化

避免共振的常用方法如下：(1)減小激振源；(2)采用隔振措施；(3)改變本體結構和剛度分布；(4)提高結構阻尼比[6]。高速動車組齒輪傳動系統的傳動形式和在轉向架下的安裝位置決定了其無法隔振和避免線路激勵源[7]，需通過對箱體結構進行優化以減小振動。根據A、B兩種型式齒輪箱模態分析結果，通過以下措施對B型齒輪箱進行優化改進設計：

(1)針對應變較大的吊掛及大小法蘭連接區域，局部箱壁厚度增加2 mm；

(2)增加上、下箱體的加強筋數量，優化加強筋的尺寸，在保證齒輪箱質量和體積相當的情況下，最大限度提升齒輪箱的總體剛度；

(3)箱體曲面采用大型弧面過渡，減少直角和棱邊的應力集中。

改進后的B型齒輪箱箱體如圖2所示。

圖2 改進后的B型高速動車組齒輪傳動系統

對改進后的B型齒輪箱箱體采用四面體二次單元進行網格劃分，計算得到改進后的B型齒輪箱前10階模態，改進前后的B型齒輪箱模態對比如表2所示。

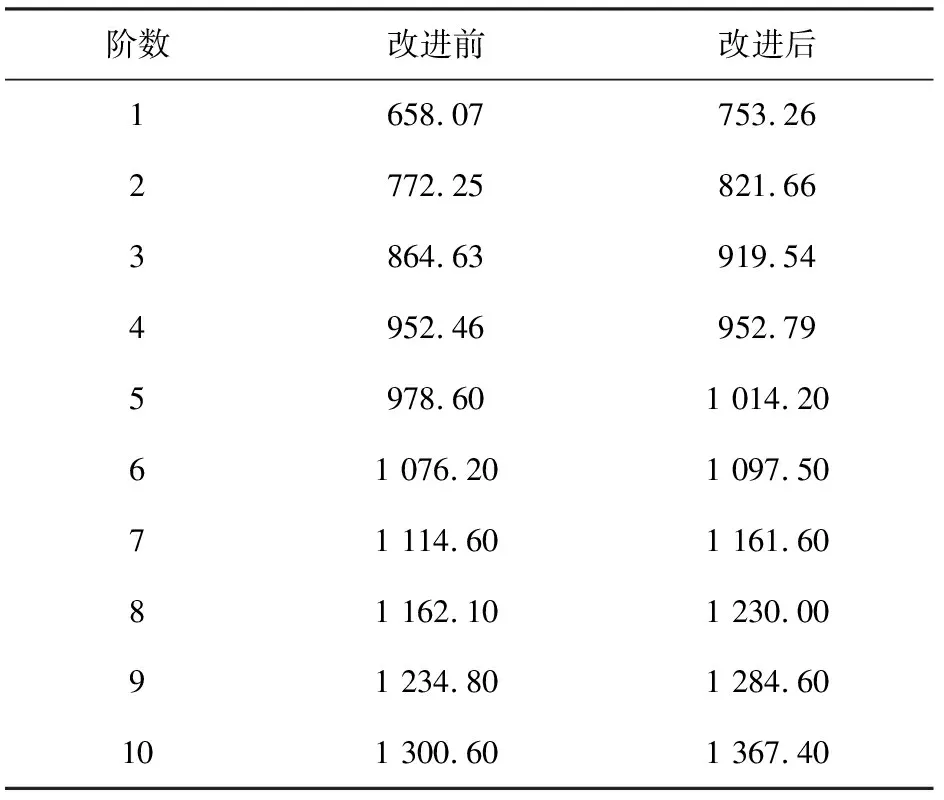
表2 改進前后的B型齒輪箱前10階自由模態頻率 /Hz

由表2可知，經優化改進后的B型齒輪箱，各階模態均有所提高，結構優化效果顯著，一階頻率進一步遠離線路不平順性對動車組輪對的激振頻率(400～600 Hz)[8]，降低了齒輪箱共振的風險，同時增強了齒輪箱的結構性能。

4 模態測試試驗

模態測試通過激振試驗對采集的振動數據進行識別處理[9]，從而得到系統的模態參數。試驗步驟如圖3所示，首先建立測量系統，然后測量頻響函數，最終進行模態參數估計。

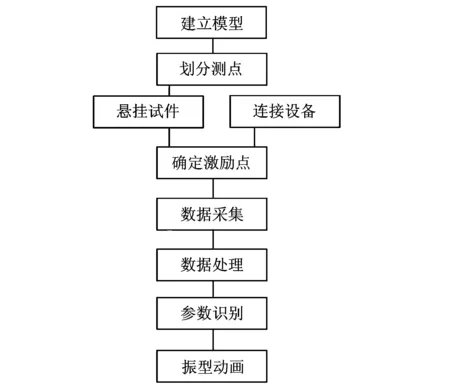
圖3 試驗步驟示意圖

模態測試試驗中，箱體自由懸掛，根據建立的模型確定測點，采用錘擊法移動力錘進行測試，力錘的脈沖激勵與一定帶寬的隨機激勵具有相似的力譜，從而能一次激出在此頻帶內的各階模態[10]。激振試驗圖如圖4所示。

圖4 試驗激振示意圖

模態測試試驗得到改進后B型動車組齒輪箱的模態，前10階模態頻率如表3所示。

表3 齒輪箱前10階模態測試頻率 /Hz

5 模態分析結論

5.1 仿真計算與試驗測試結果比較

通過對3種類型齒輪箱有限元模態分析及試驗模態分析數據的對比，發現有限元模態分析方法的結果與試驗模態分析方法的結果非常相近，誤差值的差低于15%，在可接受范圍內，驗證了有限元模態分析方法的可靠性。仿真計算與試驗測試誤差如表4所示。

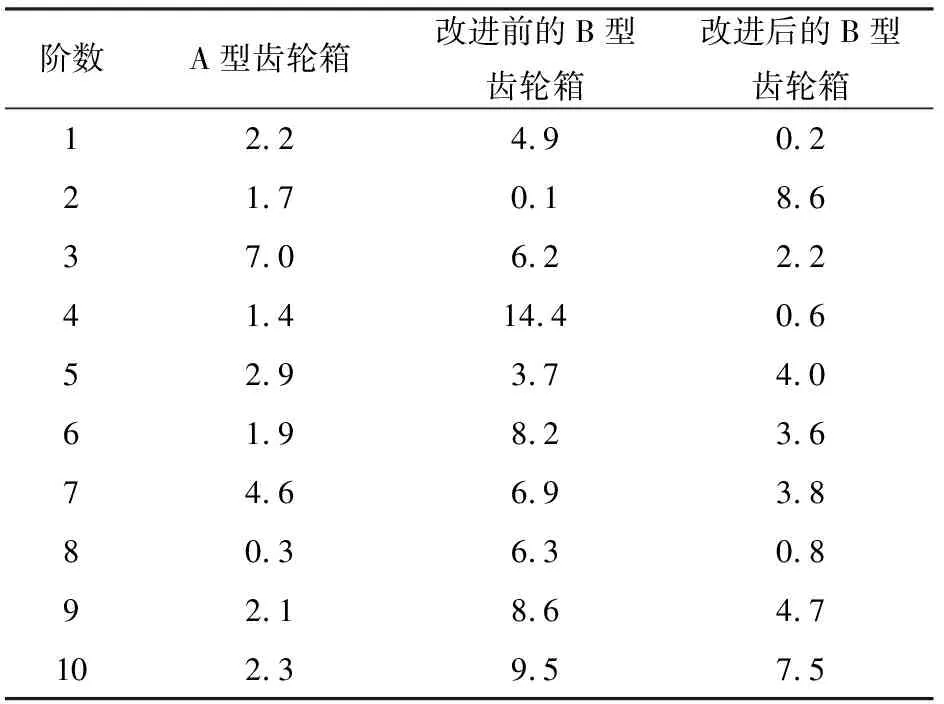
表4 仿真計算與試驗測試誤差 /%

造成齒輪箱模態仿真計算與試驗測試結果之間誤差的原因如下：(1)有限元仿真在計算過程中簡化了模型結構，略去了螺栓、倒角等細碎的特征，質量與真實情況存在誤差。(2)有限元仿真時，將齒輪箱箱體的兩部分合并作為整體(A型齒輪箱的箱體和箱蓋合并、B型齒輪箱的上下箱體合并)進行模態計算分析，試驗測試中齒輪箱箱體通過螺栓連接，兩者在箱體接合面的剛度存在誤差。(3)由于齒輪箱箱體結構和試驗條件限制，試驗測試中布置的測點有限，測點數量遠小于有限元網格劃分的節點數，相較有限元計算而言，試驗測試更容易產生模態丟失的情況。(4)仿真計算中計算箱體的自由模態，每個節點均有6個自由度，而試驗測試通過加速度傳感器測量測點的振動來獲取頻率和模態，難以識別測點的轉動自由度，自由度數不完整。(5)仿真計算時在分析過程中引入了大量假設，如材料連續性假設、均勻性假設等，同時忽略了阻尼等因素，與實際情況存在誤差。試驗測試的模型更接近于實際情況。

5.2 設計改進意見

根據模態仿真與測試結果，在齒輪箱的設計過程中應使齒輪箱的低階模態頻率避開服役中的外部激勵頻率，并增大剛度和阻尼來提高箱體共振頻率，以減小振動對齒輪箱箱體的影響。

針對應變較大區域，在設計過程中要增強該部位的剛度，例如增加局部箱壁厚度，增設加強筋，以及在零件鑄造加工成型的過程中注意該部位的缺陷和加工方式。

應對齒輪箱結構進行合理布置，在設計過程中綜合考慮質量體積以及剛度的分配與平衡，使齒輪箱總體剛度發揮到最大限度，提高齒輪箱的基頻頻率，提高齒輪箱整體的抗振能力。

結構設計過程中，應在綜合考慮零部件拆裝維修的基礎上，對齒輪箱箱體采用弧面仿形設計，同時多采用加強筋結構，提高齒輪箱的剛度、減少共振峰次數、降低振動水平。

6 總結

針對不同類型齒輪箱進行模態仿真計算及試驗測試，給出了齒輪箱結構設計的改進建議，為傳動系統后續的設計優化提供了依據，以便從設計源頭降低振動載荷對傳動平穩性的影響，滿足傳動系統減振抗振要求，提高齒輪箱結構可靠性。

在后續的研究中，將對齒輪箱模態仿真模型做出進一步改進，優化邊界條件的設置及相關參數的匹配，縮小仿真計算與實際情況的差異，提高仿真計算的可靠性。