高延性混凝土加固蒸壓加氣混凝土砌體墻抗震性能試驗研究

鄧明科，馬向琨，張 偉，李 寧

(1. 西安建筑科技大學土木工程學院，西安 710055；2. 華陸工程科技有限責任公司，西安 710065)

蒸壓加氣混凝土(autoclaved aerated concrete，AAC)砌塊砌體具有自重輕、保溫性能好、節約能耗等優勢，在村鎮建筑中具有廣泛的應用前景。但由于自身強度低，抗裂性能差，AAC砌體作為承重墻體時，抗震性能較差，目前主要應用于填充墻等非結構構件中。此外，我國最新頒布的地震區劃[1]對房屋建筑的整體抗震設防要求有所提高，而村鎮砌體結構的施工質量差且構造措施不完善，因此，為了使AAC砌體結構具有滿足設防要求的抗震性能，從而更好地推廣應用此類結構，開展AAC砌塊砌體墻的抗震加固研究具有重要意義。

國內外相關技術規程和標準規定了新建AAC墻體材料及施工方面的要求[2?4]，文獻[5 ? 6]研究了在墻體內部增設芯柱及構造柱等構造措施來改善其抗震性能。文獻[7 ? 9]分別研究了粘貼纖維織物、織物增強砂漿(textiles reinforced mortar，TRM)加固AAC砌體墻的抗震性能，研究表明，粘貼纖維織物可提高AAC墻體的承載力及變形能力，但存在耐久性較差及造價高等問題；TRM加固未能有效改善AAC墻體的脆性破壞模式。

傳統的砌體結構抗震加固方法[10?12]存在增加結構自重、耐久性較差、對原結構擾動大等較突出的問題，因此不適用于現有AAC砌體墻的抗震加固。目前，工程水泥基復合材料(engineered cementitious composite，ECC)已應用于砌體結構加固領域，并取得了良好的加固效果[13?18]，為推廣其應用，本課題組采用ECC設計理論制備了高延性混凝土(high ductility concrete，HDC)，在拉伸和剪切作用下表現出高延展性，具有典型的多裂縫開展和應變硬化特征，并對其加固磚砌體墻的抗震性能開展了系統研究[16?23]。研究表明，HDC面層及構造帶加固方式可提高砌體墻的整體性，改善砌體墻的脆性破壞模式。

為探究一種經濟有效、施工方便且適用于廣大村鎮AAC砌體墻的加固方法，本文提出采用HDC單面加固、雙面條帶加固及雙面配筋條帶加固AAC砌體墻的方式，通過低周反復荷載試驗，分析各加固墻體的破壞形態、滯回性能及剛度退化；研究不同加固方式對AAC砌體承重墻抗震性能的影響，并且根據各試件的破壞形態給出了相應的承載力計算公式，為此類結構的加固設計提供依據。

1 試驗概況

1.1 試件設計與制作

試驗共制作了6片AAC砌塊砌體墻，包括4片無構造柱墻體和2片構造柱約束墻體。試件AWG-0和AWG-1為構造柱約束墻體，其余均為無筋砌體墻。試件AW-0和AWG-0為未加固試件，試件AW-1和AWG-1均采用單面壓抹15 mm厚HDC面層加固，試件AW-2和AW-3分別采用雙面20 mm厚HDC條帶和雙面20 mm厚HDC配筋條帶加固，配筋條帶中豎向鋼筋為φ6@120 mm，水平分布鋼筋為φ6@300 mm，兩側條帶用φ6@300 mm拉筋拉結。各試件的加固方式詳見表1。

表 1 加固方式Table 1 Retrofitting form of specimens

墻體由鋼筋混凝土加載頂梁、蒸壓加氣混凝土砌體墻及底梁構成。墻體的高寬比為0.62，構造柱截面尺寸為120 mm×190 mm，構造柱內縱筋為4φ6，箍筋為φ6@200 mm，試件的詳細尺寸見圖1。為提高墻體與HDC加固層的粘結性能，加固之前先對墻體水平灰縫進行勾縫處理(剔鑿8～10 mm深度的灰縫)，再壓抹HDC加固層。

1.2 試驗材料

圖 1 試件尺寸 /mmFig.1 Details of specimens

試驗墻體均采用A5.0級AAC砌塊和水泥砂漿砌筑，砌筑砂漿的厚度為10 mm。試驗選用的AAC砌塊的主要塊型為600 mm×240 mm×190 mm，按標準試驗方法[2]測得其立方體抗壓強度平均值為3.5 MPa。砌筑砂漿及構造柱混凝土的抗壓強度分別采用邊長為70.7 mm和100 mm的立方體試塊，與墻體同條件養護28 d后測定，測試結果見表2。本次試驗中所用鋼筋均為φ6，試驗測得其屈服強度平均值為375 MPa。

表 2 材料實測強度Table 2 Measured strength of materials

HDC為粉煤灰、水泥、礦物摻合料、砂和PVA纖維等按一定比例配制而成，其中PVA纖維的體積摻量為1.7%，PVA纖維的各項力學性能指標見表3；由邊長為100 mm的立方體試塊測得的HDC抗壓強度平均值為59.80 MPa；采用三個尺寸為350 mm×50 mm×15 mm的啞鈴型試件測試HDC的抗拉強度和拉應變，其抗拉強度平均值為3.89 MPa，極限拉應變最大值達到1.25%。其中一個試件的單軸拉伸應力-應變曲線如圖2所示。

表 3 PVA纖維各項性能指標Table 3 Performance indicators of PVA

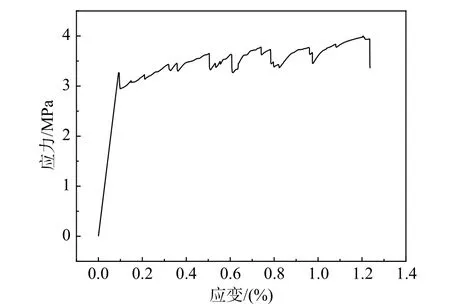
圖 2 HDC應力-應變曲線Fig.2 Stress-strain curves of HDC

1.3 加載制度及測點布置

本次試驗采用擬靜力試驗加載方法[24]，并采用荷載-變形雙控制分級加載。加載初期采用荷載控制，并分級加載，荷載級差為10 kN；當荷載-位移曲線明顯彎曲后采用位移控制，位移級差為2 mm，且每級反復推拉3次，直至AAC砌體墻承載能力下降至極限荷載的85%以下，停止試驗加載。

試驗加載裝置如圖3所示。在加載梁中部布置一個位移計，以測試AAC砌體墻的頂點水平位移；底梁端部布置一個位移計，以測試墻體的整體滑移；墻面沿對角線方向布置兩個位移計，以測試墻體的剪切變形。

圖 3 加載裝置Fig.3 Loading device

2 試驗結果及分析

2.1 破壞過程

2.1.1 無構造柱試件

規定加載過程中荷載與位移的數值均以推方向為正、拉方向為負。

1)試件AW-0

當加載至90 kN時，墻體底部出現水平裂縫；隨后，裂縫逐漸延伸；加載至110 kN時，荷載-位移曲線明顯彎曲，改為由位移控制加載。加載至2 mm時，墻體出現階梯狀裂縫，并沿墻體對角方向延伸；加載至4 mm時，試件達到峰值荷載132.3 kN，此時，墻面形成多條斜裂縫，最終形成交叉斜裂縫；加載至8 mm時，斜裂縫寬度達8 mm，且局部砌塊掉落，荷載降至峰值荷載的85%以下，試驗停止加載。

2)試件AW-1

當加載至100 kN時，墻體底部出現彎曲裂縫；加載至?110 kN時，荷載-位移曲線彎曲，改為由位移控制加載。當加載至4 mm時，墻體達到峰值荷載170.6 kN，未加固側底層砌塊多處被壓碎；加載至?4 mm時，HDC面層底部裂縫貫通且墻體產生了明顯的滑移；當頂點位移達到14 mm時，加固面層底部水平裂縫寬度達10 mm，水平荷載仍無明顯下降，此時，試驗停止加載。

3)試件AW-2

當加載至?100 kN時，墻體南側面底部出現水平裂縫；加載至120 kN時，試件南側面出現斜裂縫，且荷載-位移曲線彎曲，此后試件按位移控制加載。當加載到2 mm時，HDC條帶加腋處出現少量斜裂縫；加載至4 mm時，墻體達到峰值荷載145.6 kN，此時，HDC條帶加腋處斜裂縫延伸變寬；隨著位移增大，北側條帶開始剝離；當加載至8 mm時，北側條帶大面積脫落，荷載明顯下降，試驗停止加載。

4)試件AW-3

峰值荷載前，試件AW-3與試件AW-2現象類似。峰值荷載后，HDC條帶加腋處裂縫變寬；此后隨頂點位移增加，墻體南側面中部灰縫裂縫貫通；當頂點位移達到14 mm時，HDC條帶加腋處斜裂縫延伸至頂梁且面層外鼓，荷載明顯下降，停止加載。

2.1.2 帶構造柱試件

1)試件AWG-0

當加載至70 kN時，墻體底部出現水平裂縫；加載至?110 kN時，墻體出現斜裂縫，位移-荷載曲線彎曲，改為由位移控制加載。當加載到2 mm時，墻體斜裂縫變寬并延伸至構造柱；當加載至4 mm時，主斜裂縫相交，試件達到峰值荷載119.67 kN；加載至?4 mm時，兩側構造柱出現新的水平裂縫；此后隨頂點位移增加，裂縫延伸變寬，當加載至12 mm時，墻體裂縫最大寬度達7 mm；當加載至14 mm時，墻體角部砌塊壓碎，水平荷載降至峰值荷載的85%以下，試驗停止加載。

2)試件AWG-1

峰值荷載以前，試件AWG-1與試件AWG-0試驗現象相似；峰值荷載后，隨位移增加，兩側構造柱與砌體墻交接處，HDC面層出現豎向裂縫，并且未加固墻面根部出現受壓裂縫；加載至10 mm時，面層兩側豎向裂縫擴展，且未加固墻面底部砌塊壓碎；此時，水平荷載明顯下降，試驗停止加載。

各試件破壞時的裂縫分布如圖4所示。

2.2 破壞形態分析

1) 試件AW-0發生對角剪切破壞，墻面出現大量斜裂縫，表現出明顯的脆性破壞特征。

2) HDC面層提高了墻體的對角剪切強度并限制了墻體的開裂，試件AW-1墻面未出現裂縫。墻體底部首先出現彎曲裂縫，且輕微搖擺；隨后，底部水平裂縫逐漸貫通，未加固側底部砌塊壓碎，墻體沿底部滑移；試件AW-1最終發生剪切滑移破壞，終止加載時，試件的水平荷載未明顯下降。

圖 4 試件的裂縫分布Fig.4 Crack distribution of specimens

3) 相比試件AW-3，試件AW-2缺乏錨固措施，因HDC條帶與AAC墻體材料性能不同，在荷載作用下二者變形不協調，條帶因內側邊緣處缺乏約束，首先在此處發生剝離；加載后期，HDC條帶受壓外鼓，進一步導致條帶剝落，使得試件承載力迅速下降；隨位移增加，墻面斜裂縫延伸、變寬，試件發生對角剪切破壞；相比試件AW-0，試件AW-2墻面裂縫數量明顯減少。

4) 試件AW-3最終發生對角剪切破壞；相比試件AW-2，HDC配筋條帶與墻體粘結較好，可為試件AW-3提供較好的約束，明顯減小墻體的損傷，改善墻體的破壞形態。

5) 試件AWG-0最終發生對角剪切破壞，墻面出現多條斜裂縫，且構造柱出現彎曲裂縫；構造柱可為墻體提供約束作用，因此，相比試件AW-0，試件AWG-0破壞時墻面裂縫數量明顯減少，損傷程度較輕。

6) HDC面層良好的約束效果使得試件AWG-1墻體底部首先出現水平裂縫，峰值荷載前，面層未發生破壞。由于砌塊與構造柱強度差異大，峰值荷載后，彎曲作用使得此處砌塊被壓碎，導致HDC面層外鼓、開裂，出現兩條豎向裂縫；未加固墻面出現數條斜裂縫，并且不斷延伸、變寬；墻體最終發生彎剪破壞，相比試件AWG-0，試件AWG-1破壞時墻面裂縫數量明顯減少。

2.3 滯回曲線及骨架曲線

圖5給出了6個試件的荷載-位移滯回曲線，由圖5分析可得：AAC墻體在開裂前，荷載-位移曲線基本呈直線；開裂后，墻體進入彈塑性變形階段，曲線斜率逐漸減小，墻體剛度下降；相比未加固試件，加固試件的破壞模式有所改善，滯回曲線更加飽滿，說明試驗所采取的加固方式能有效提高AAC砌體墻的滯回性能。

1) 試件AW-0滯回環數量較少，墻體開裂后滯回環面積即顯著增大，捏縮效應顯著；HDC單面加固試件AW-1的彈性變形能力明顯提高，峰值荷載后，墻體底部滑移且部分砌塊被壓碎，導致滯回環捏攏現象明顯，但其數量及所圍面積均有所增加，表現出較好的耗能能力；HDC條帶的約束作用使得試件AW-2承載力有所提高，但峰值荷載后條帶剝離，導致承載力迅速下降，曲線整體與試件AW-0相似；相比試件AW-2，試件AW-3的滯回環更加飽滿，呈“弓”型，且數量明顯增加，反映出較好的變形和耗能能力，因此，HDC配筋條帶可為墻體提供較好的約束。

2) 相比試件AW-0，構造柱的約束作用使得墻體AWG-0的滯回環數量增加但捏攏現象更加明顯；對于試件AWG-1，峰值荷載后墻體兩側砌塊被壓碎，導致承載力迅速下降；相比試件AWG-0，HDC面層改變了試件AWG-1的破壞模式，其水平承載力明顯提高，滯回環數量有所減少但所圍面積增大。

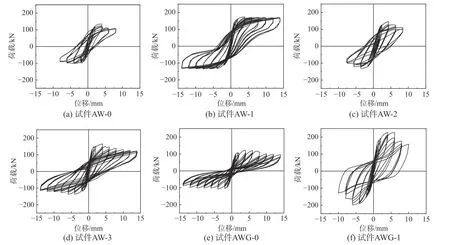
圖 5 滯回曲線Fig.5 Hysteretic curves

各試件的骨架曲線如圖6所示。取墻面出現第一條可見裂縫時所對應的荷載和位移確定其開裂荷載和開裂位移；根據“能量等值法”確定各試件的屈服荷載和屈服位移；由試驗停止加載時的位移確定試件的極限位移。各試件在上述特征點處的荷載及位移見表4。由圖6和表4分析可得：

1) 試件AWG-0的極限位移和位移延性系數分別為試件AW-0的1.74倍和1.81倍，說明構造柱的約束作用可大幅提高墻體的變形能力。

2) 對于無構造柱試件，加固試件的開裂荷載、峰值荷載均有所提高，且峰值荷載后的強度退化較為平緩。相比試件AW-0，試件AW-1、AW-2和AW-3的峰值荷載分別提高了31%、17%和28%，極限位移分別提高了74%、5%(條帶剝離)和75%；加固試件AW-1、AW-3的位移延性系數分別提高了40%和66%。

3) 相比試件AWG-0，試件AW-3的峰值荷載提高了32%，且極限位移與之相近，說明HDC配筋條帶可發揮類似圈梁-構造柱對墻體的約束作用，從而提高墻體的水平承載力與變形能力。

4) 對于構造柱約束試件，相比試件AWG-0，試件AWG-1的開裂荷載及峰值荷載分別提高了57%和86%，且試件AWG-1的殘余承載力高于試件AWG-0的峰值荷載，說明試件可繼續承受荷載，其變形能力尚未得到充分發揮。

圖 6 骨架曲線Fig.6 Skeleton curves

表 4 各試件特征點Table 4 Characteristic points of specimens

2.4 剛度退化

以各加載級割線剛度與其所對應的頂點位移變化曲線來研究各試件在加載過程中的剛度退化規律，如圖7所示。

1) 對于無構造柱試件，峰值荷載后，單面加固及雙面配筋條帶加固墻體的剛度退化曲線相對平緩，說明此類加固方法可延緩無筋AAC墻體的剛度退化；由于HDC條帶剝離，試件AW-2的剛度退化曲線與試件AW-0較為接近。

2) 對于帶構造柱試件，由于HDC面層的約束作用，試件AWG-1的初始剛度大幅提高，加載初期的剛度退化明顯；峰值荷載后，墻體根部砌塊壓碎，HDC面層外鼓，導致其剛度退化較快。

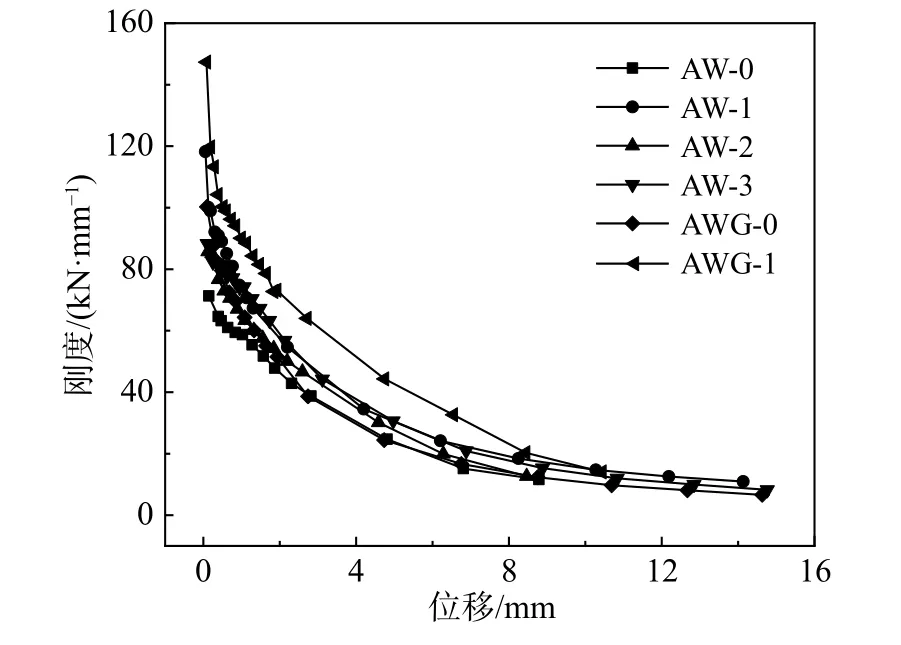
圖 7 剛度退化曲線Fig.7 Rigidity retrogradation curves

2.5 耗能能力

各試件達到屈服荷載、峰值荷載及破壞荷載時的累積耗能見表5。

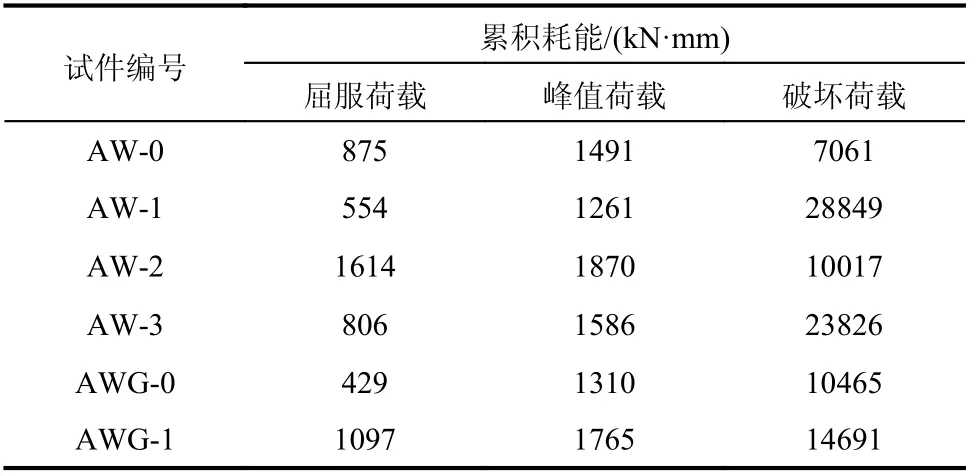
表 5 試件的累積耗能Table 5 Cumulated energy depletion of specimens

由表5分析可得：

1) 對于無構造柱試件，HDC加固試件破壞時的總耗能均有大幅提高，其中試件AW-1、AW-2與AW-3的總耗能分別是未加固試件AW-0的4.1倍、1.4倍(條帶剝落)和3.4倍。

2) 相比試件AW-0，由于構造柱的約束作用，試件AWG-0的總耗能提高了48%。相比試件AWG-0，試件AWG-1的總耗能提高了40%；停止加載時，試件AWG-1的殘余承載力較高，墻面損傷較小，說明其耗能能力尚未得到充分發揮。

3 承載力分析

本文所述的6個試件在試驗中分別產生了三種破壞形態：對角剪切破壞、剪切-滑移破壞和彎剪破壞。根據各試件的加固形式及其破壞形態，可按下述方法計算其水平承載力。

3.1 未加固試件受剪承載力

1) 未加固試件AW-0發生對角剪切破壞，可根據主拉應力強度理論，按我國規范[25]中給出的承載力計算公式計算墻體的受剪承載力：

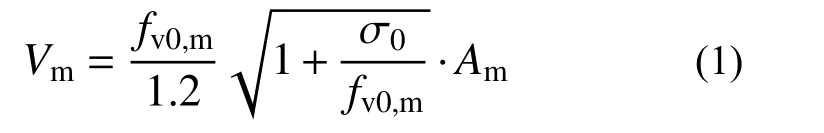
式中：σ0為AAC砌體墻的豎向壓應力；Am為AAC砌體墻的橫截面面積；fv0,m為AAC砌體墻抗剪強度的平均值，可參考《砌體結構設計規范》[26]按下式計算：

式中：f2為砂漿的抗壓強度平均值；k5為系數，本文取0.09。

2) 對于試件AWG-0，考慮墻體兩側構造柱的約束作用，按下式計算其受剪承載力[16]：

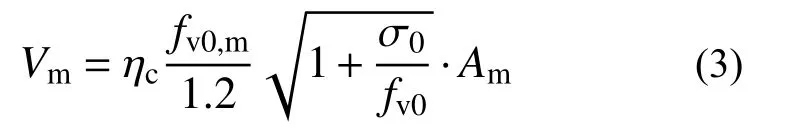
式中：ηc為構造柱約束增強系數，可按我國規范[27]相關規定取值，本文砂漿抗壓強度平均值3.1 MPa，取ηc=1.25。

3.2 HDC加固墻體水平承載力

1) HDC單面加固試件AW-1發生剪切滑移破壞；因此，以底部截面為控制截面，根據剪摩強度理論計算該試件的受剪承載力。

試件底部截面受力狀態如圖8所示。忽略開裂區域墻體的抗剪強度，將受壓區作為墻體的有效抗剪截面；根據平衡條件，試件AW-1的水平承載力計算如下[17?18]。

由平截面假定及力的平衡條件可得：

對截面中點取矩可得：

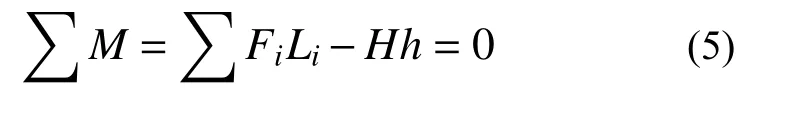
式中：Em為AAC砌體墻的彈性模量；EH為HDC的彈性模量；xc為截面未開裂區域長度，為簡化計算，取為墻體長度的一半，xc=1215 mm；FN1為截面受壓區AAC砌體墻合力；FN2為受壓區HDC面層合力；FT1、FT2分別為截面受拉區HDC面層未開裂段合力和開裂段合力[18]；Li為上述各合力作用點到截面中點所對應的距離。

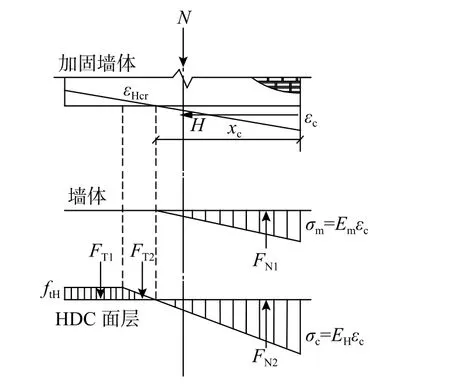
圖 8 截面受力狀態示意圖Fig.8 Schematic diagram of stress state of cross section

H為墻體底部有效受剪截面內的剪力，可用下式計算：

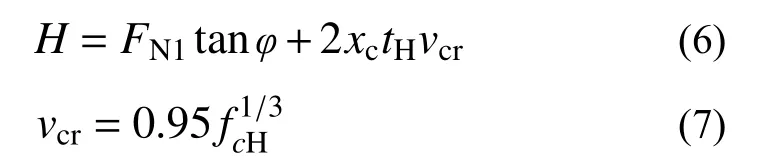
式中：φ為砂漿內摩擦角[18]；vcr為HDC截面剪切強度[28]；fcH為HDC軸心抗壓強度，由立方體平均抗壓強度換算得到[22]。

2) 為便于設計計算，本文采用疊加法計算試件AWG-1的水平承載力：

式中：Vm為加固試件中原砌體墻的水平承載力，按式(3)計算，VH為HDC面層的受剪承載力，根據本課題組以往研究成果，按下式計算[29]：

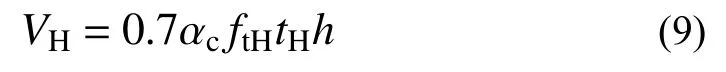
式中：αc為HDC強度利用系數，取0.7；ftH為HDC抗拉強度；tH為HDC面層厚度；h為墻體水平方向長度。

3) 在荷載作用下HDC條帶與弱框架的作用類似。因此，引入等效受壓斜撐模型計算試件AW-2及AW-3的受剪承載力。如圖9所示，將原砌體墻等效為一個沿墻體對角線方向、具有特定寬度及力學性能的斜撐，將HDC條帶等效為墻體兩側的構造柱，并采用疊加法來計算HDC條帶加固墻體的受剪承載力[30?31]：

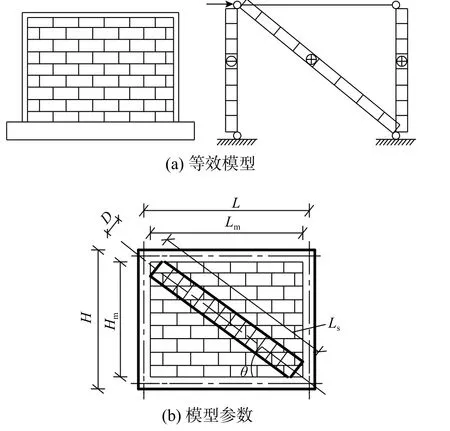
圖 9 約束磚砌體墻的等效受壓斜撐模型Fig.9 Equivalent compressive diagonal bracing model for constrained-brick masonry walls

為原砌體墻的受剪承載力，按下式計算：

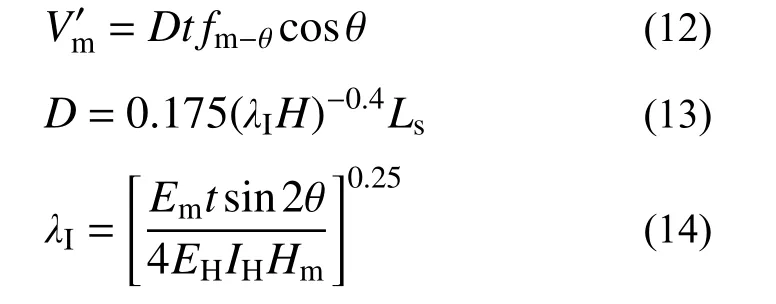
式中：t為墻體厚度；fm-θ為砌體沿斜撐方向的抗壓強度，本文近似取fm-θ=0.85fm[31]；D為斜撐寬度；H為圈梁中線之間的構造柱高度；Ls為受壓斜撐的長度；λI為計算受壓斜撐寬度的參數；Em為墻體材料的彈性模量；EH為HDC條帶部分等效彈性模量；IH為HDC條帶部分等效慣性矩；Hm為墻體高度；θ為受壓斜撐與水平方向的夾角；fm為AAC砌體的抗壓強度平均值，可參考我國規范[26]按下式計算：

式中：α為與塊體高度及砌體類別有關的參數，本文取0.5；k1為與塊體類別有關的參數，本文取0.78；f1為AAC砌塊抗壓強度平均值；k2為修正系數，本文取1.0。

3.3 計算結果驗證

本次試驗各試件的水平承載力計算結果與試驗結果如表6所示。

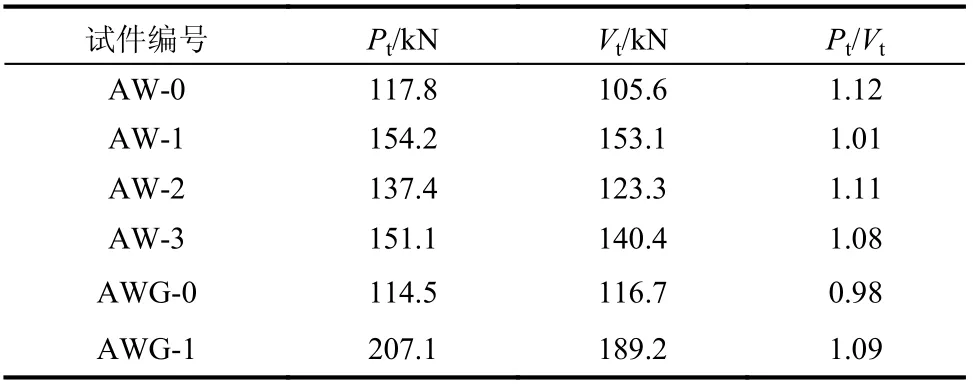
表 6 計算結果與試驗結果比較Table 6 Comparison of maximum loads

由表6可知，本文采用的HDC加固蒸壓加氣混凝土砌塊砌體墻的水平承載力計算方法，其計算值與試驗值基本吻合，可為此類構件的加固設計提供參考。但是，本次試驗的試件數量較少，后期將開展進一步的試驗及理論分析。

4 結論

通過2片未加固AAC墻體和4片采用HDC加固的AAC墻體的試驗研究結果，可初步得到以下結論：

(1) HDC面層及配筋條帶加固可對AAC墻體形成有效約束，從而提高無筋AAC砌體墻的延性及耗能能力。加固后墻體的水平承載力及耗能能力均高于構造柱約束墻體，且變形能力與之相近，這兩種方式可作為提高AAC墻體抗震性能的有效加固措施。

(2) 單面HDC面層加固構造柱約束AAC墻體破壞時，墻體損傷較小，殘余承載力較高，有利于結構的震后修復及在余震中繼續承受荷載。

(3) 雙面HDC條帶加固的試件出現了HDC條帶剝落，未能充分發揮HDC條帶的加固效果，但雙面配筋條帶加固的試件未出現剝落。因此，通過錨固措施防止HDC條帶剝落，可以充分發揮HDC條帶的加固效果。

(4) 基于試驗中AAC砌體墻的破壞模式，提出了各加固方式下AAC砌體墻的水平承載力計算方法，可為HDC加固AAC墻體受剪承載力計算提供參考。