高轉(zhuǎn)矩密度的聚磁Halbach少極差磁齒輪設計與優(yōu)化

李 輝，戴太陽，盧 敏，袁 彬，殷 毅

(重慶大學 輸配電裝備及系統(tǒng)安全與新技術(shù)國家重點實驗室,重慶 400044)

0 引 言

磁齒輪相比機械齒輪具有低噪聲、無摩擦、高效率、高耐久和自適應過載保護等優(yōu)勢，有望在未來替代機械傳動機構(gòu)[1-3]。然而，現(xiàn)階段磁齒輪的轉(zhuǎn)矩密度一般在100～290 kN·m/m3，而機械式齒輪容許轉(zhuǎn)矩密度則可達到700 kN·m/m3以上，磁齒輪還面臨轉(zhuǎn)矩密度有待提高的問題[4-6]。

提高磁齒輪轉(zhuǎn)矩密度的方法是增加磁耦合，以提高氣隙磁密中的有效諧波分量，改變磁齒輪拓撲結(jié)構(gòu)是增加磁極耦合的有效手段。文獻[7]提出調(diào)制型磁齒輪拓撲，采用同心式結(jié)構(gòu)，但需要在內(nèi)外轉(zhuǎn)子之間放入調(diào)制環(huán)鐵心產(chǎn)生雙層氣隙結(jié)構(gòu)，大大增加了內(nèi)外轉(zhuǎn)子之間的氣隙長度，使得漏磁增加，磁極耦合程度不高，氣隙磁密中有效諧波幅值難以提高，轉(zhuǎn)矩密度可達100 kN·m/m3，且由于其轉(zhuǎn)矩和傳動比之間的約束關(guān)系，當傳動比高于20∶1時，轉(zhuǎn)矩密度會出現(xiàn)下降趨勢[8]。文獻[9]提出少極差磁齒輪(以下簡稱MGSPD)拓撲，采用偏心式結(jié)構(gòu)，利用內(nèi)外轉(zhuǎn)子偏心產(chǎn)生的不均勻氣隙調(diào)制磁場[10]，無需使用調(diào)磁塊，由此只需單層氣隙結(jié)構(gòu)即可實現(xiàn)變速傳動，大大提高了氣隙磁密，其表貼式MGSPD轉(zhuǎn)矩密度在傳動比20∶1時達180 kN·m/m3。文獻[11]提出聚磁MGSPD結(jié)構(gòu)，通過優(yōu)化其轉(zhuǎn)矩密度可達291 kN·m/m3，傳動比25∶1。文獻[12]將Halbach結(jié)構(gòu)應用到MGSPD，轉(zhuǎn)矩密度達294 kN·m/m3。但是上述結(jié)構(gòu)轉(zhuǎn)矩密度仍然偏低，需要探索一種轉(zhuǎn)矩密度更高的磁齒輪結(jié)構(gòu)。

本文將聚磁結(jié)構(gòu)和Halbach結(jié)構(gòu)進行組合，提出聚磁Halbach MGSPD(以下簡稱FFHMGSPD)結(jié)構(gòu)，進一步提高了磁齒輪的轉(zhuǎn)矩密度，但是其結(jié)構(gòu)參數(shù)更加復雜。為深入研究各個參數(shù)對FFHMGSPD轉(zhuǎn)矩的影響，通過控制變量法逐一分析新型拓撲的各結(jié)構(gòu)參數(shù)與輸出轉(zhuǎn)矩的關(guān)系,并根據(jù)分析結(jié)果對初始設計方案進行了優(yōu)化。

1 FFHMGSPD工作原理

FFHMGSPD拓撲結(jié)構(gòu)，轉(zhuǎn)子運動及磁鋼充磁方向如圖1所示。ω1表示內(nèi)轉(zhuǎn)子自轉(zhuǎn)角速度，ω2表示內(nèi)轉(zhuǎn)子圓周平動角速度，ω3表示外轉(zhuǎn)子自轉(zhuǎn)角速度。由永磁體充磁方向可以看出，周向充磁的磁鋼和鐵心塊構(gòu)成聚磁結(jié)構(gòu)，與徑向充磁磁鋼構(gòu)成Halbach結(jié)構(gòu)。該結(jié)構(gòu)相比Halbach結(jié)構(gòu)可以使用更少的稀土材料，相比普通聚磁結(jié)構(gòu)，徑向充磁的磁鋼可以進一步引導磁力線的走向，提高聚磁效果。

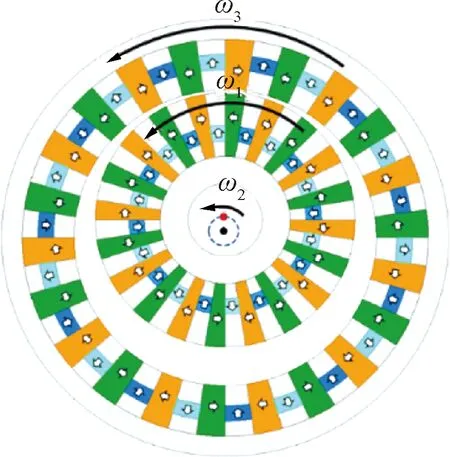
圖1 FFHMGSPD拓撲

FFHMGSPD的傳動結(jié)構(gòu)和運行機理與機械擺線齒輪相同，在運行時，外轉(zhuǎn)子固定(ω3=0)，內(nèi)轉(zhuǎn)子既自轉(zhuǎn)也進行圓周平動，兩種運動方向相反，若設內(nèi)轉(zhuǎn)子極對數(shù)為p1，外轉(zhuǎn)子極對數(shù)為p2，則傳動比：

(1)

圖2以一臺外轉(zhuǎn)子極對數(shù)p1=11、內(nèi)轉(zhuǎn)子極對數(shù)p2=10為例，展示了不同時刻FFHMGSPD的運動過程。當內(nèi)轉(zhuǎn)子圓周平動θ=360°時，內(nèi)轉(zhuǎn)子在外轉(zhuǎn)子磁場作用下正好自轉(zhuǎn)一對轉(zhuǎn)子磁極角度360°/p1。

圖2 FFHMGSPD運動示意圖

2 模型參數(shù)計算

圖3為FFHMGSPD結(jié)構(gòu)參數(shù)示意圖。圖3中，p1、p2為內(nèi)外轉(zhuǎn)子極對數(shù)，β1為內(nèi)轉(zhuǎn)子周向充磁永磁體跨距角，β2為內(nèi)轉(zhuǎn)子徑向充磁永磁體跨距角，α1為外轉(zhuǎn)子周向充磁永磁體跨距角，α2為外轉(zhuǎn)子徑向充磁永磁體跨距角，h1、h8為內(nèi)外轉(zhuǎn)子軛部厚度，h2、h7為內(nèi)外轉(zhuǎn)子齒高，h3、h6為內(nèi)外轉(zhuǎn)子徑向充磁永磁體充磁方向厚度，h4、h5為內(nèi)外轉(zhuǎn)子周向充磁永磁體徑向高度，r0、r1為內(nèi)轉(zhuǎn)子周向充磁永磁體內(nèi)外徑，r2、r3為外轉(zhuǎn)子周向充磁永磁體內(nèi)外徑，e為內(nèi)轉(zhuǎn)子的偏心量，l為軸向長度，g為最小氣隙長度。以上部分參數(shù)有如下約束關(guān)系：

圖3 FFHMGSPD結(jié)構(gòu)參數(shù)

r1=r0+h4

(2)

r2=r3-h5

(3)

e=r2-r1-g

(4)

(5)

(6)

設計指標如表1所示，則峰值輸出轉(zhuǎn)矩T：

表1 FFHMGSPD設計參數(shù)

(7)

則FFHMGSPD體積：

(8)

取軸向長度l=35 mm，則可得r3=160 mm。為了布置軸承的空間足夠，內(nèi)轉(zhuǎn)子周向永磁體內(nèi)徑取r0=91.5 mm。由于傳動比G=25∶1，根據(jù)式(1)，可取p2=26，如果選取更高的極對數(shù)，則會極大地增加磁鋼裝配過程復雜程度，不利于樣機制造。

通過以上分析，磁鋼材料和固定的結(jié)構(gòu)參數(shù)如表2所示。為了方便對比轉(zhuǎn)矩密度，永磁體材料采用與文獻[12]中剩磁相同的永磁體NMX41SH。需要進行參數(shù)掃描的結(jié)構(gòu)參數(shù)，其初始值如表3所示。由式(2)～式(4)可知，當h4，h5，r0，r3和g確定后，r1，r2和e就已確定，故表3中沒有列入r1，r2和e。

表2 FFHMGSPD材料和結(jié)構(gòu)參數(shù)

表3 FFHMGSPD初始掃描參數(shù)

3 結(jié)構(gòu)參數(shù)優(yōu)化

根據(jù)前文所得的初始設計方案，建立FFHMGSPD初始有限元模型，其結(jié)構(gòu)示意圖如圖4所示。采用控制變量法探究表3中各個結(jié)構(gòu)參數(shù)與FFHMGSPD轉(zhuǎn)矩T之間的關(guān)系。

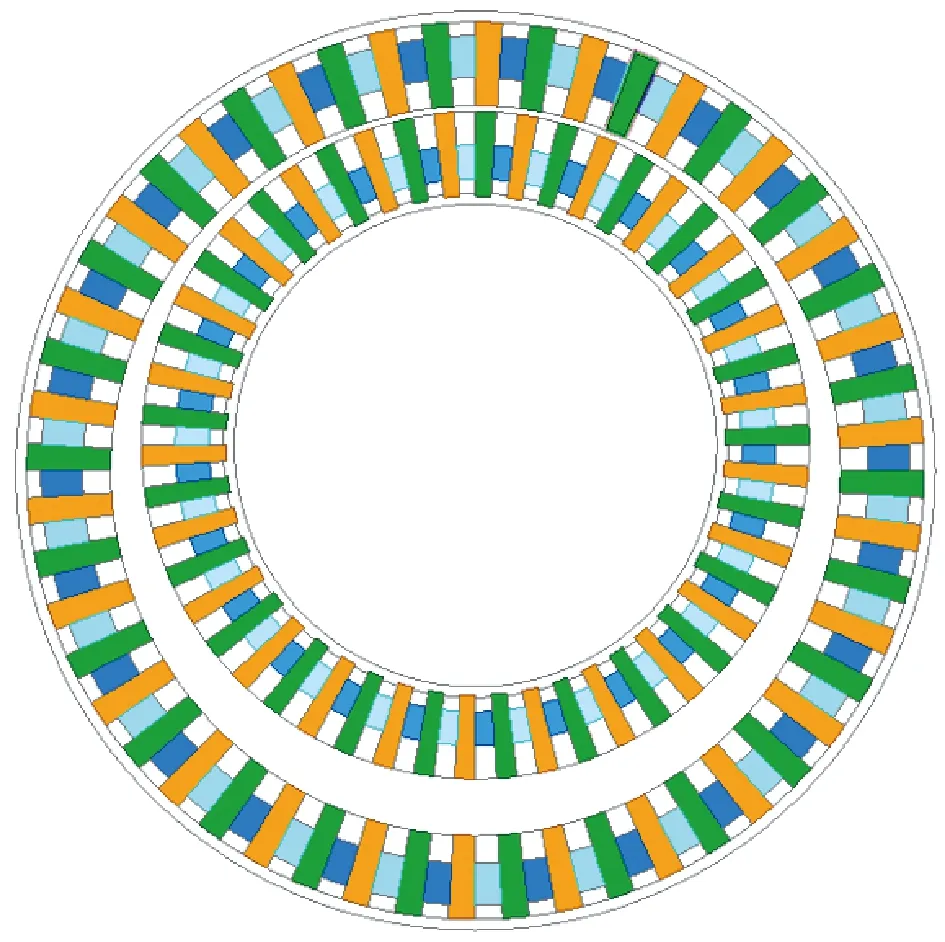
圖4 FFHMGSPD初始結(jié)構(gòu)示意圖

3.1 最小氣隙長度g與T關(guān)系

圖5表示最小氣隙長度g與峰值輸出轉(zhuǎn)矩T之間的關(guān)系。由圖5可知，T是g的一次函數(shù)，且g對T的影響很大，隨g增大，T將減小。但是，g不可取太小，以防止內(nèi)外轉(zhuǎn)子之間單邊磁拉力太大，增加裝配工藝難度，并對軸承使用壽命產(chǎn)生影響，可取g=1.5 mm。

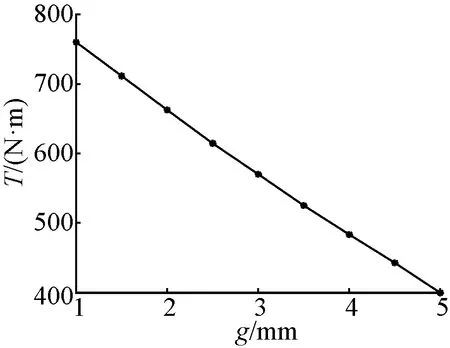
圖5 g與T關(guān)系

3.2 內(nèi)外轉(zhuǎn)子軛部厚度h1,h8與T關(guān)系

圖6表示在初始方案下，只改變內(nèi)轉(zhuǎn)子軛部厚度h1情況下的峰值轉(zhuǎn)矩變化。由圖6可知，h1對FFHMGSPD峰值轉(zhuǎn)矩影響較小，且當h1=0時，T取最大值。圖7表示只改變外轉(zhuǎn)子軛部厚度h8時的峰值轉(zhuǎn)矩變化。由圖7可知，h8對峰值轉(zhuǎn)矩影響也較小，且當h8=0時，T取最大值。由以上結(jié)果可知，聚磁Halbach結(jié)構(gòu)，內(nèi)外轉(zhuǎn)子不需要增加軛部鐵心，該優(yōu)勢將有利于減小齒輪體積，降低材料使用量，從而減小運動部件慣量，提高響應速度。

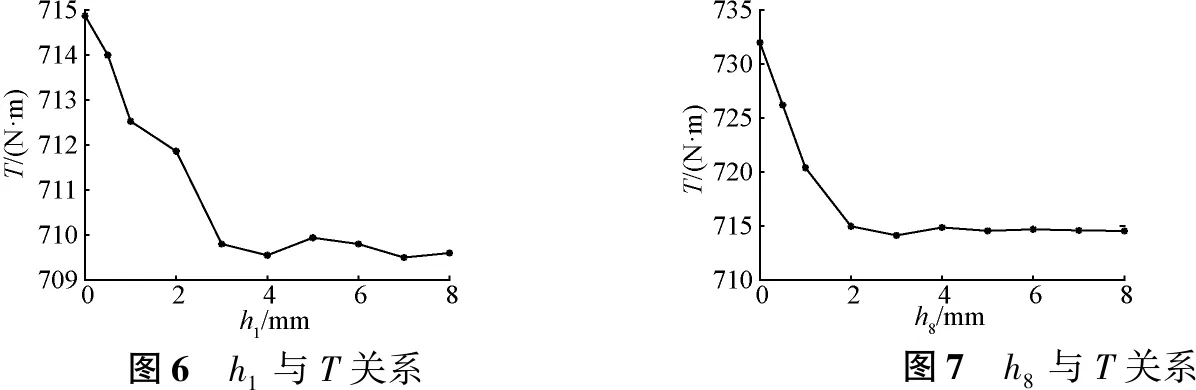
圖6 h1與T關(guān)系圖7 h8與T關(guān)系

3.3 內(nèi)外轉(zhuǎn)子周向充磁永磁體徑向厚度h4,h5與T關(guān)系

由式(4)可知，內(nèi)外轉(zhuǎn)子齒高h2，h7和徑向充磁永磁體充磁方向厚度h3，h6受內(nèi)外轉(zhuǎn)子周向充磁永磁體徑向高度h4，h5限制，故先分析h4，h5與T的關(guān)系。圖8為保持其他參數(shù)不變，單獨改變內(nèi)外轉(zhuǎn)子周向充磁永磁體徑向高度h4，h5的情況下，峰值輸出轉(zhuǎn)矩的變化情況。由圖8可知，隨著h4和h5的增加，T先快速增加，之后趨于平緩，可取拐點h4=29 mm，h5=35 mm，若繼續(xù)增加永磁材料，峰值轉(zhuǎn)矩增大的收益則會減小。

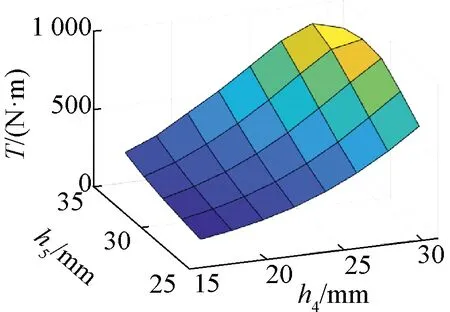
圖8 h4,h5與T關(guān)系

3.4 內(nèi)轉(zhuǎn)子齒高h2和內(nèi)轉(zhuǎn)子徑向充磁永磁體充磁方向厚度h3與轉(zhuǎn)矩T關(guān)系

圖9顯示內(nèi)轉(zhuǎn)子齒高h2和內(nèi)轉(zhuǎn)子徑向充磁永磁體充磁方向厚度h3發(fā)生變化時，峰值輸出轉(zhuǎn)矩的變化情況。齒高h2對T的影響較小，內(nèi)轉(zhuǎn)子徑向充磁永磁體厚度h3對T影響較大，且隨著h3增加，T增加的幅度逐漸趨于平緩，可取拐點h2=3 mm，h3=20 mm。

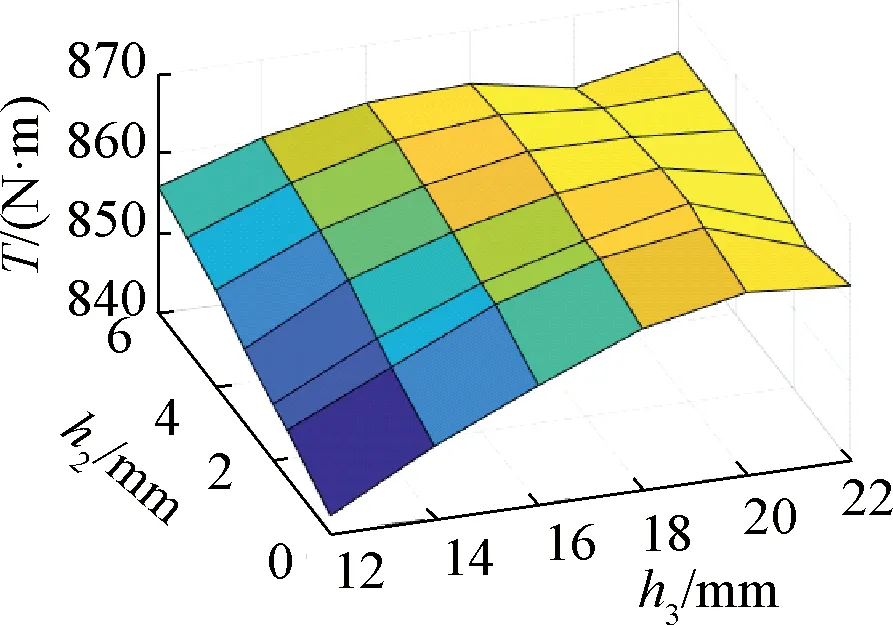
圖9 h2和h3與T關(guān)系

3.5 外轉(zhuǎn)子齒高h7和外轉(zhuǎn)子徑向充磁永磁體充磁方向厚度h6與轉(zhuǎn)矩T關(guān)系

圖10顯示外轉(zhuǎn)子齒高h7和外轉(zhuǎn)子徑向充磁永磁體充磁方向厚度h6發(fā)生變化時，峰值輸出轉(zhuǎn)矩的變化情況。由圖10可知，外轉(zhuǎn)子齒高h7對T的影響較小，外轉(zhuǎn)子徑向充磁永磁體厚度h6對T影響較大，且隨著h6增加，T先增加后減小，可取最高點h6=15 mm，h7=0 mm。

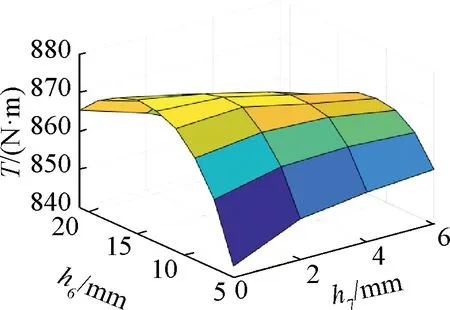
圖10 h6和h7與T關(guān)系

3.6 內(nèi)外轉(zhuǎn)子磁鋼跨距角比例i，j與轉(zhuǎn)矩T關(guān)系

圖11和圖12顯示內(nèi)外轉(zhuǎn)子磁鋼跨距角發(fā)生變化時，靜態(tài)電磁轉(zhuǎn)矩隨磁矩角變化曲線，也即磁矩角特性曲線簇(磁矩角即為內(nèi)外磁鋼產(chǎn)生磁場夾角的電角度，類似同步電機的功角)。由圖11、圖12可知，當i和j從1/1變化成其它比例時，矩角特性曲線發(fā)生移相，且峰值靜態(tài)電磁轉(zhuǎn)矩減小，故內(nèi)外轉(zhuǎn)子跨距角比例取i=1/1，j=1/1。

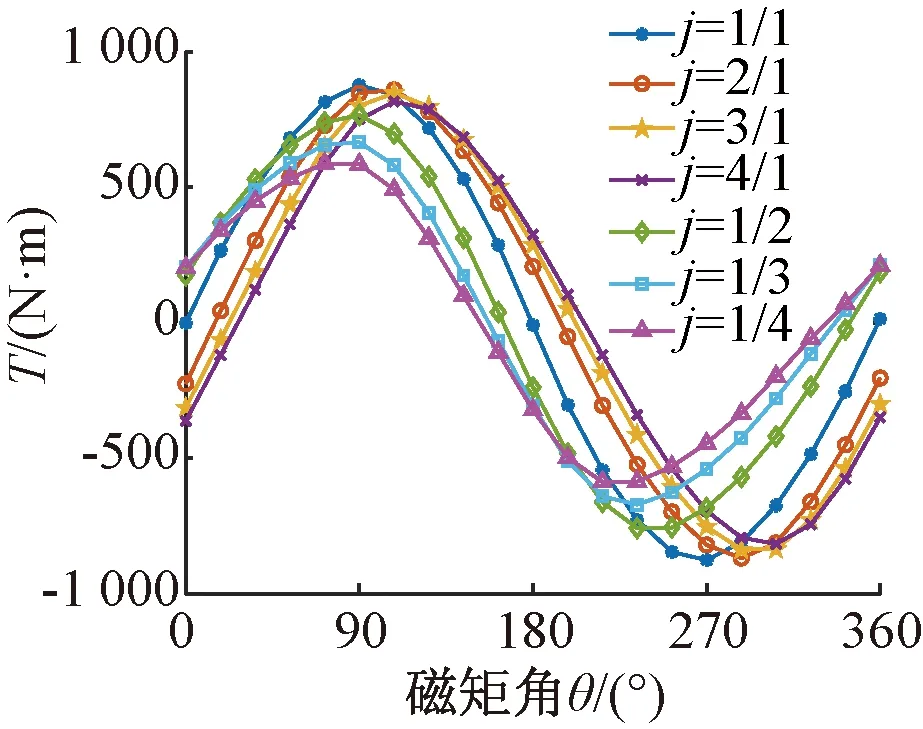
圖11 j與T關(guān)系

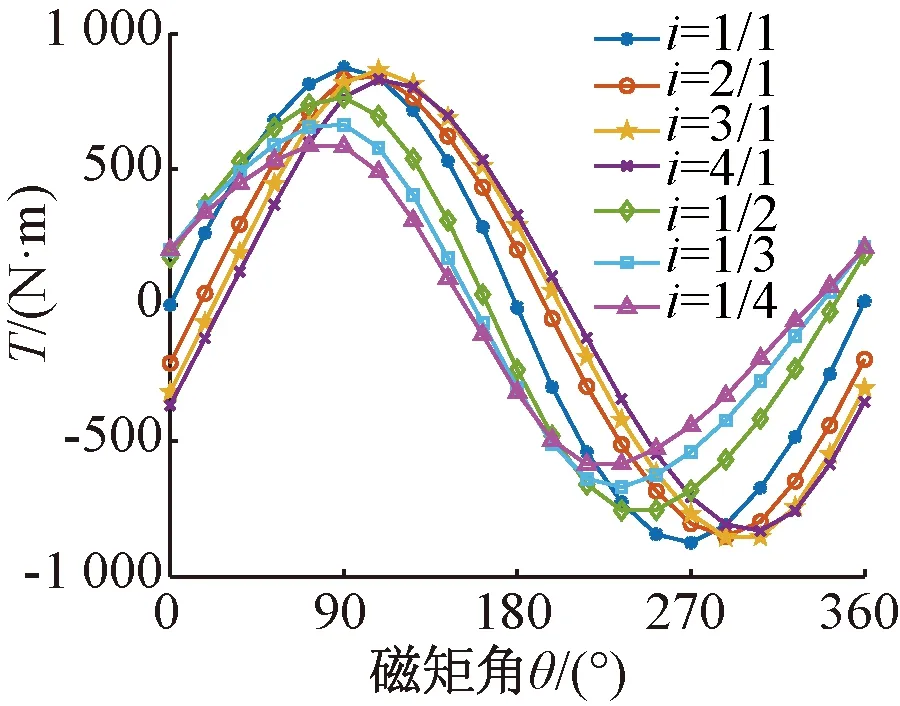
圖12 i與T關(guān)系

3.7 設計方案優(yōu)化

通過以上分析，最終設計方案的模型結(jié)構(gòu)參數(shù)如表4所示，優(yōu)化后的二維結(jié)構(gòu)如圖13所示。對其進行有限元計算，其剖分結(jié)果、磁密和磁力線云圖如圖14所示。由磁場分布云圖可知，雖然該拓撲取消了磁軛，但是磁力線依然可以正常閉合，實現(xiàn)內(nèi)外磁鋼磁場之間的耦合，從而傳遞扭矩。其徑向氣隙磁密波形如圖15所示，由氣隙磁密分布曲線可知，氣隙磁密成對稱分布，對稱軸即為FFHMGSPD幾何對稱軸，氣隙磁密幅值為2.3 T。

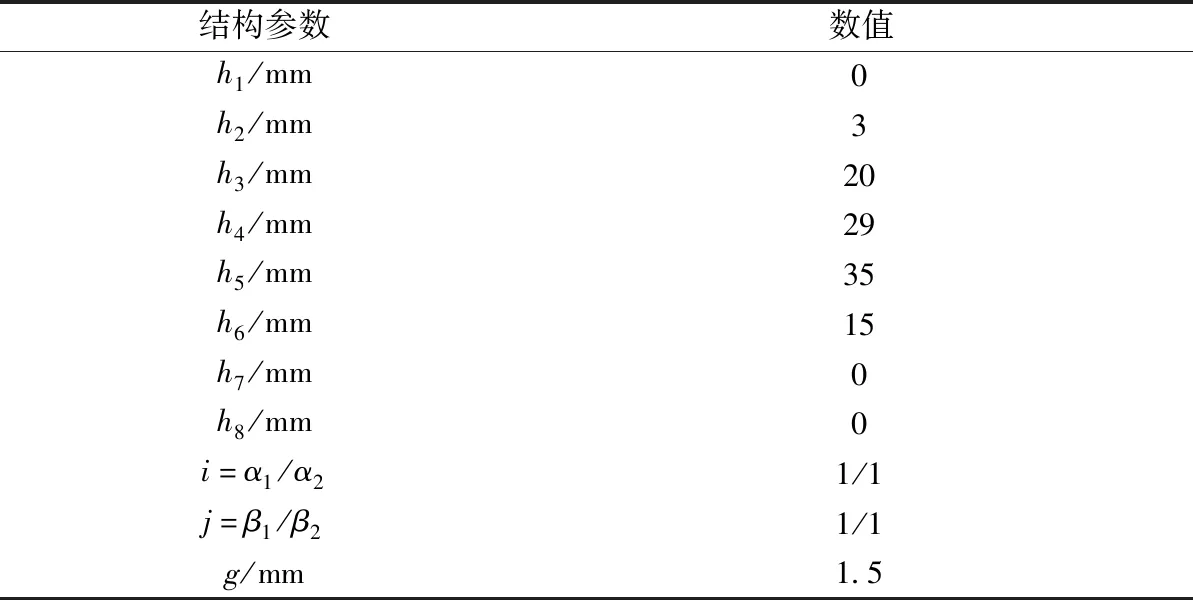
表4 FFHMGSPD最終設計方案

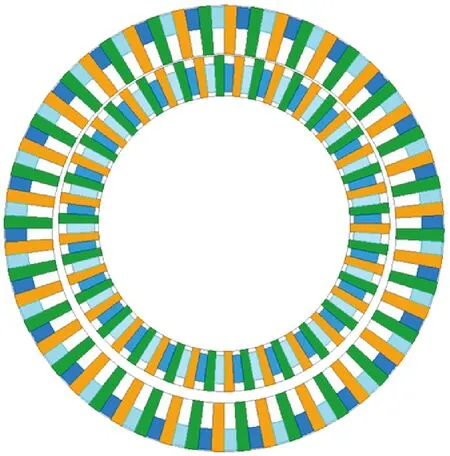
圖13 優(yōu)化設計方案結(jié)構(gòu)示意圖

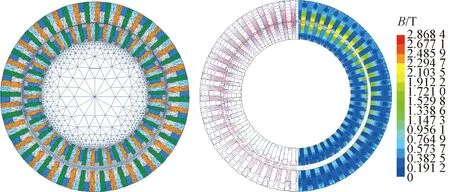
圖14 有限元剖分圖和磁場云圖

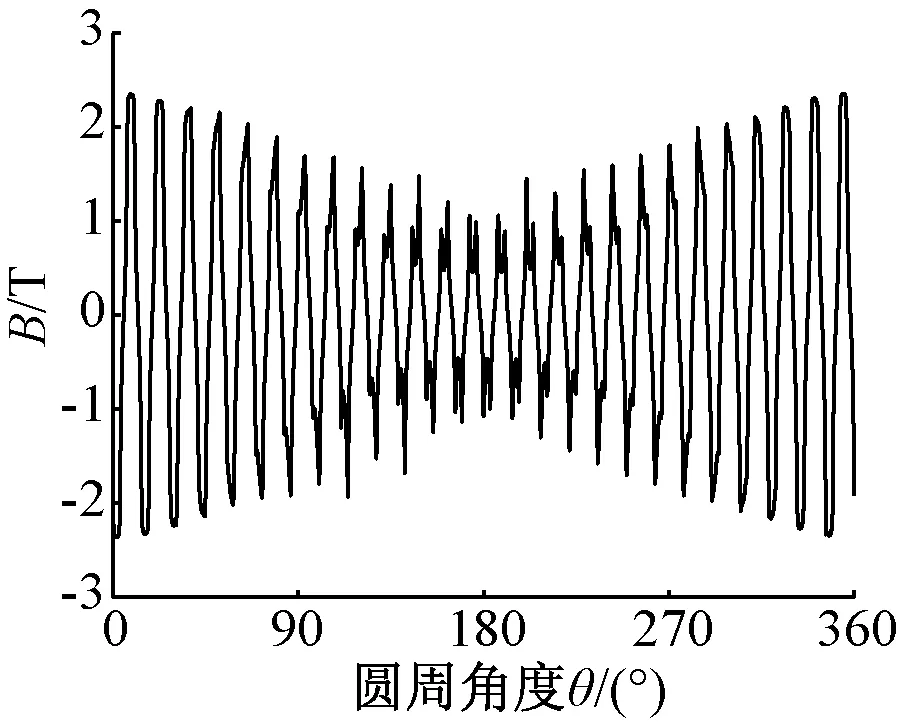
圖15 氣隙磁密曲線

使用有限元軟件計算出磁場分布以后，使用麥克斯韋張量法即可得到內(nèi)轉(zhuǎn)子上所受電磁轉(zhuǎn)矩[13]：

(9)

式中：μ0為空氣磁導率；ne為氣隙曲面s上的單位法向矢量；r為徑向矢量。

圖16為優(yōu)化前后靜態(tài)電磁轉(zhuǎn)矩隨磁矩角對比圖，優(yōu)化前模型峰值靜態(tài)電磁轉(zhuǎn)矩為605 N·m，優(yōu)化后模型峰值靜態(tài)電磁轉(zhuǎn)矩可達875 N·m，提高了44%，轉(zhuǎn)矩密度達310.8 kN·m/m3，相比表貼式結(jié)果的180 kN·m/m3，提高了72%。

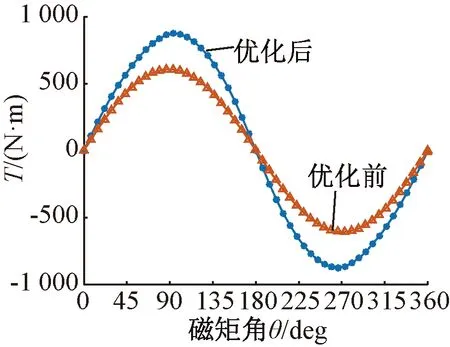
圖16 優(yōu)化前后矩角特性對比

單位有效部分質(zhì)量轉(zhuǎn)矩由下式計算：

π(ρm-ρs)l[(r0+h2+h3)2-(r0+h2)2+

(r3-h7)2-(r3-h7-h6)2]}-1

(10)

可達75 N·m/kg，相比聚磁結(jié)構(gòu)的64 N·m/kg[11]，高出17%。

當FFHMGSPD以額定轉(zhuǎn)速100 r/min帶動恒定負載Tload=800 N·m運行時，其輸出轉(zhuǎn)矩穩(wěn)定后如圖17所示。由轉(zhuǎn)矩波形可知，輸出轉(zhuǎn)矩脈動率僅為1.9%，磁齒輪可以平穩(wěn)地帶動負載運行。

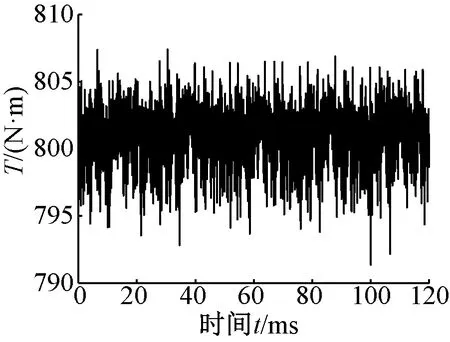
圖17 接恒定負載時的輸出轉(zhuǎn)矩曲線

4 結(jié) 語

為提高MGSPD轉(zhuǎn)矩密度，本文提出聚磁Halbach少極差磁齒輪(FFHMGSPD)結(jié)構(gòu)，建立了有限元模型，通過控制變量法研究了FFHMGSPD結(jié)構(gòu)參數(shù)與輸出轉(zhuǎn)矩之間的關(guān)系，并根據(jù)分析結(jié)果對初始設計進行了優(yōu)化，分析結(jié)果如下。

1)最小氣隙長度g，內(nèi)外轉(zhuǎn)子周向充磁永磁體徑向高度h4和h5，內(nèi)外轉(zhuǎn)子徑向充磁永磁體厚度h3和h6對FFHMGSPD轉(zhuǎn)矩影響較大；內(nèi)外轉(zhuǎn)子軛部厚度h1和h8對FFHMGSPD轉(zhuǎn)矩影響較小；內(nèi)外轉(zhuǎn)子磁鋼跨距角比例j和i會影響矩角特性相位和峰值大小，都取1/1時，峰值轉(zhuǎn)矩最大。

2)優(yōu)化后FFHMGSPD輸出轉(zhuǎn)矩達875 N·m，相比優(yōu)化前提高了44%，其轉(zhuǎn)矩密度可以達到310 kN·m/m3以上，單位質(zhì)量轉(zhuǎn)矩密度達到75 N·m/kg，相比表貼式結(jié)構(gòu)提高了72%，相比聚磁結(jié)構(gòu)提高了17%，轉(zhuǎn)矩脈動僅為1.9%，磁齒輪可以平穩(wěn)帶動負載運行。