一個四元數矩陣方程組通解的復矩陣極秩

吳恒飛

（亳州學院 電子與信息工程系，安徽 亳州 236800）

近些年矩陣表達式的極大秩、極小秩是矩陣論研究的熱點問題，這一課題在經濟學、工程技術等領域有著廣泛的應用，許多學者對此做了大量的工作，得到了可喜的研究成果［1-3］.文獻［4］討論了陣方程BX±X*B*=A的一般解，得到矩陣表達式A-BX±X*B*約束極秩公式，文獻［5］提出了方程組A1X=C1，XB2=C2，A3XB3=C3，A4XB4=C4一般解的極秩公式，文獻［6］研究了文獻［5］中的方程組解中的子矩陣的極秩及其他性質，文獻［7］討論了四元數矩陣方程AXB=C通解中的復分量的極大秩、極小秩及其相關應用.本文論旨在研究四元數矩陣方程組AXB=C的一般形式，即：

通解中的復矩陣的極秩，給出其純非復解的充要條件，其中A1∈Hm×p，C1∈Hm×q，B2∈Hq×s，C2∈Hp×s，A3∈Hk×p，A4∈Hn×p，B3∈Hq×r，B4∈Hq×l，C3∈Hk×r，C4∈Hn×l，為已知矩陣，X∈Hp×q為未知矩陣.

為敘述方便，用Cm×n，Hm×n分別代表全體m×n階復矩陣和四元數矩陣的集合，A+，，r（A）分別表示矩陣A的Moore-Penrose廣義逆、A的共軛和A的秩，LA=I-A+A，RA=I-AA+分別表示矩陣A的左、右誘導算子，R（A），N（A）分別表示矩陣A的列右空間和行左空間，In表示n階單位矩陣.

1 四元數方程組通解的復矩陣極秩

對任意矩陣G∈Hm×n，記G=G0+G1j，（G0，G1∈Cm×n），稱φ（G）=為G的復 表示矩陣.

引理1［8］任意矩陣M，N∈Hm×n，有：

（1）φ（MN）=φ（M）φ（N），φ（M+N）=φ（M）+φ（N），φ（M）=φ（N）?M=N；

（3）任意矩陣Y∈C2m×2n，存在X∈Hm×n，使

（4）r[φ（M）]=2r（M），φ（RM）=Rφ（M），φ（LM）=Lφ（M）.

根據矩陣的復表示及引理1，可得定理1.

定理1四元數矩陣方程組（1）有解的充要條件是方程組：

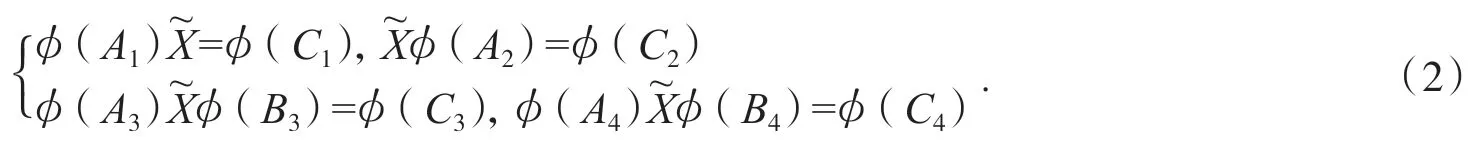
有解.

證若方程組（1）有解，則存在矩陣∈Hp×q使方程組（1）成立，把代入方程組（1）并作如下變換，即：

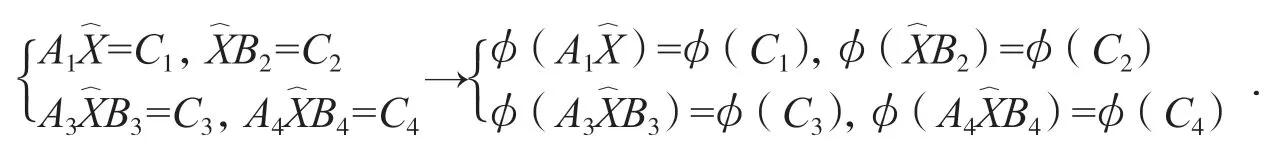
由引理1可得：

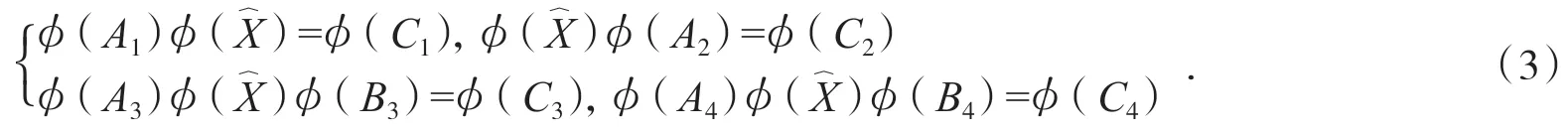
由（3）式知方程組（2）有特解φ（）.

反之，若Y∈C2p×2q是方程組（2）的解，將Y代入方程組（2）并作如下變換，即：

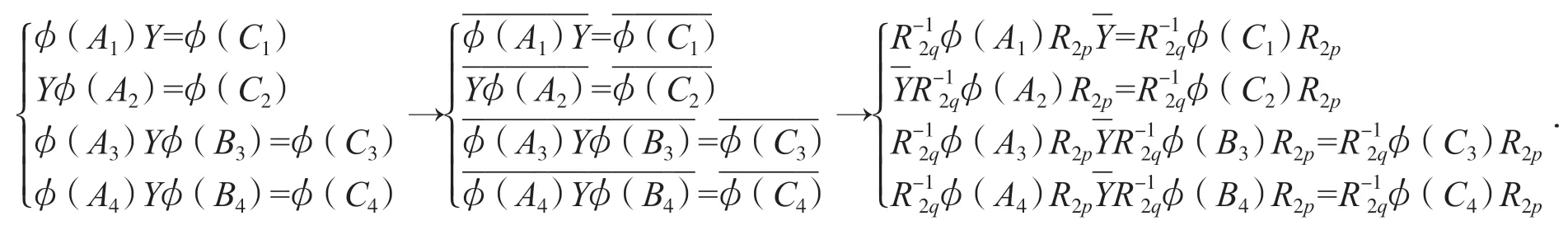
引理2［9］已知矩陣A∈Hm×n，A3∈Hm×p1，A4∈Hm×p2，B3∈Hq1×n，B4∈Hq2×n.則矩陣表達式P（X1，X2）=A+A3X1B4+A4X2B4滿足：

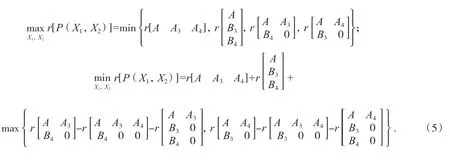
若R（A3）?R（A4），N（B4）?N（B3），則：

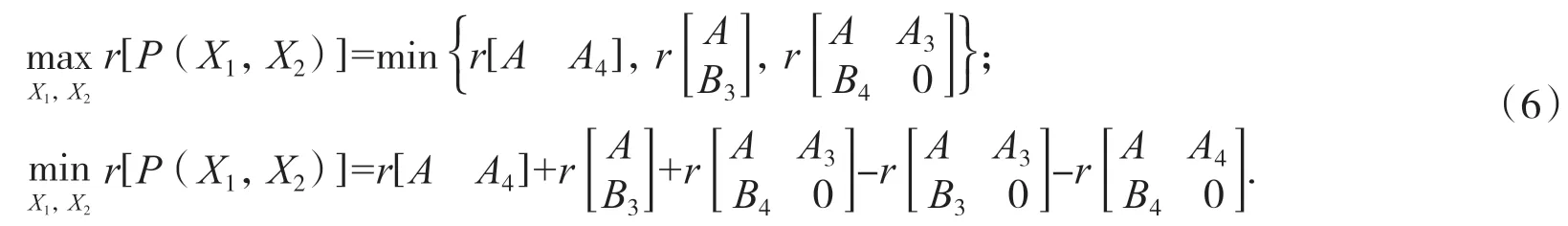
引理3［5］若方程組（1）有解，則其通解可表示為：

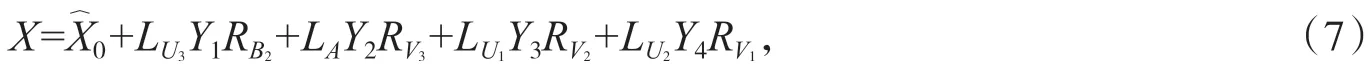
其中：V1=[B2B3]，V2=[B2B4]，V3=[B2B3B4]，，S=A3LA1，T=A4LA1，U=RB2B3，V=RB2B4，W=TLS，Z=RUV，（Y1，Y2，Y3，Y4）是任意的，是其一個特解.

容易驗證：LA1LS=LU1，LA1LT=LU2，LA1LSLW=LU3，RURB2=RV1，RVRB2=RV2，RZRURB2=RV3，則由引理1可知：

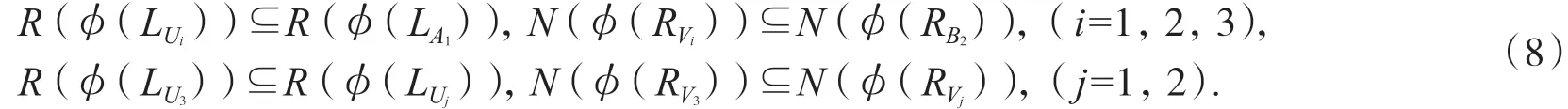
引理4［10］已知A∈Hm×t，B∈Hm×k，C∈Hl×n，D∈Hs×k，E∈Hl×p是任意矩陣，則有：

若方程組（1）有解，其解的復分量集合記為：

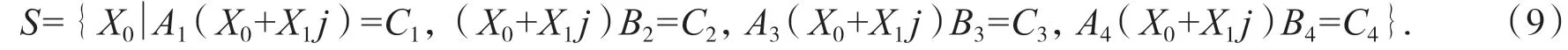
在解集S中，關于矩陣方程組（1）的解的復分量X0，結合上述引理，可得定理2.

定理2若四元數矩陣方程組（1）有解X=X0+X1j，則其解中的復分量X0滿足：

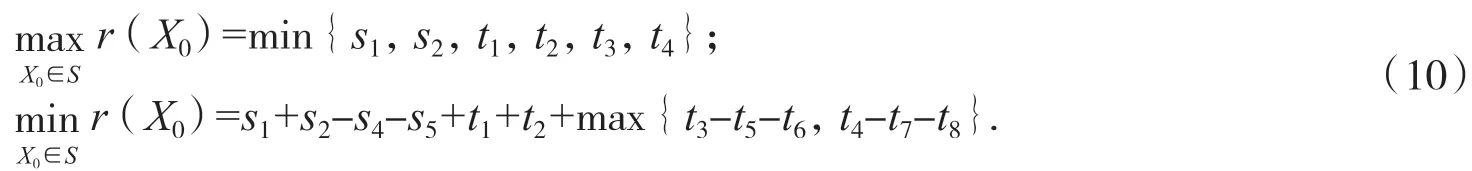
其中si，tj（i=1，2，4，5，j=1，2，…，8）可由引理2的公式（5）和公式（6）得出.

證若方程組（1）有解，則方程組（2）有解，設（2）的特解為φ（），根據引理3，方程組（2）的通解表達式為：

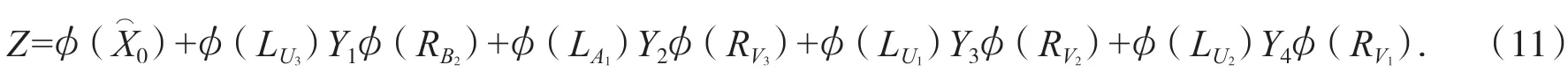
令：

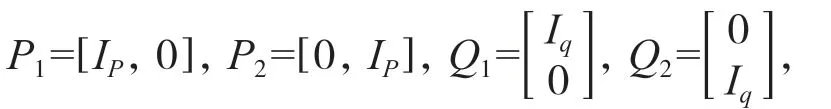
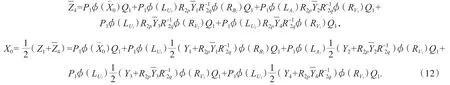
令：

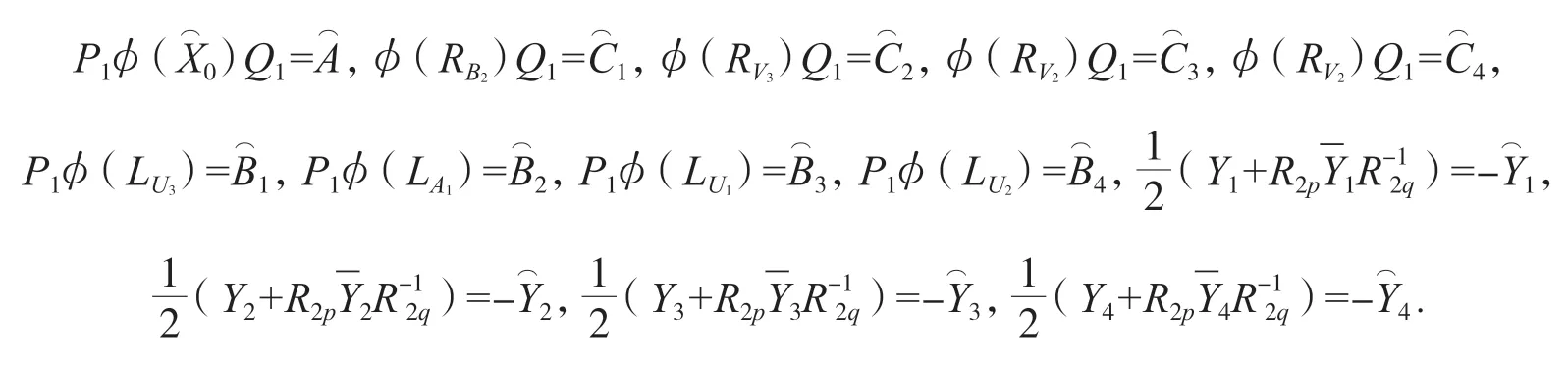
代入（12）式得：

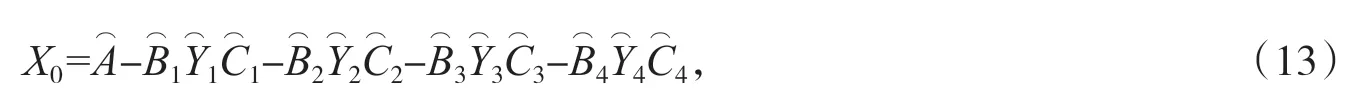
由公式（8）可知：

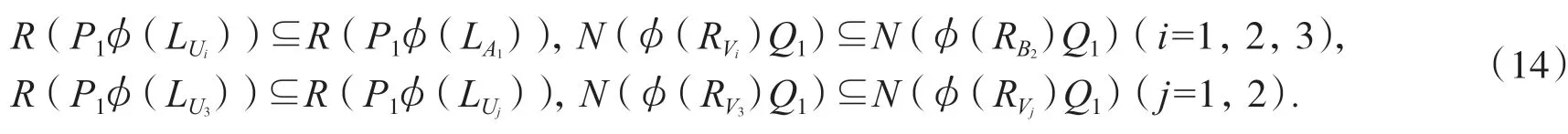
即：

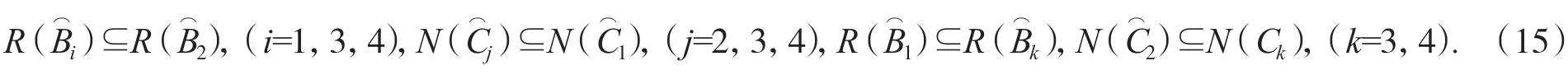
根據引理2公式（6），結合（15）式得：

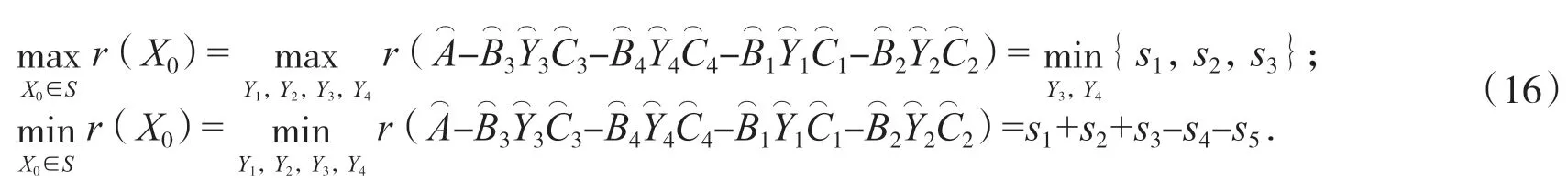
再由引理2、引理1、引理4得：

同樣的方法可證s1，s2，s5.

對s3進行變換時，無法消除其中的Y3和Y4，因此按（18）式進行計算.由引理2公式（6）可知：

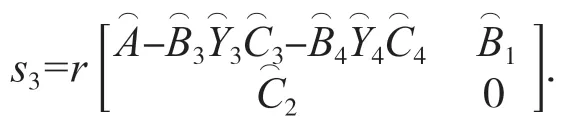
令：

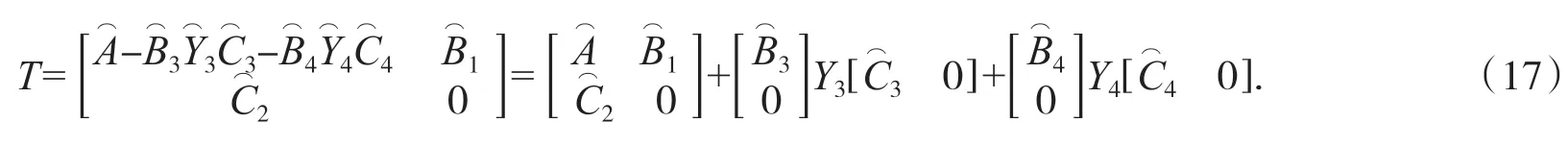
則s3=r（T），把（17）式代入引理2的公式（5）可得：

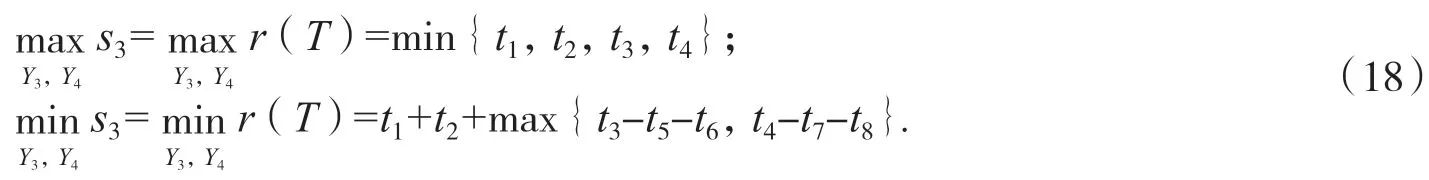
利用同樣的方法可證t2-t8，將t1-t8代入（18）式，再將（18）式和s1，s2，s4，s5代入（16）式，可證定理2成立.

與文獻［5］、文獻［6］相比，本定理結論把四元數矩陣方程組（1）轉變成等價的復矩陣方程組，縮小了數域，提升了計算的可操作性.本文討論一般形式，更有利于該理論的推廣.因此，本定理的結論擴展了四元數矩陣方程（組）通解的復矩陣分量的極秩理論.

2 復矩陣極秩的應用

作為應用，根據定理2，限定解的特殊形式，推出方程組（1）純非復矩陣解存在的充分必要條件，可得定理3.

定理3四元數矩陣方程組（1）可解，則：

a.方程組（1）至少存在一個純非復矩陣解的充要條件為：

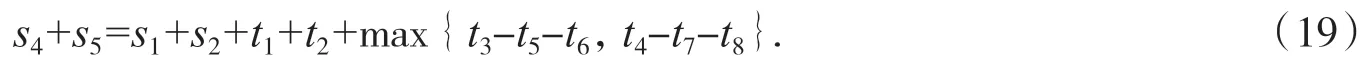
其中si，tj（i=1，2，4，5，j=1，2，3，4，5，6，7，8）同定理2中si，tj表達形式一致.

b.方程組（1）所有解都是純非復矩陣解的充要條件為：

證四元數矩陣方程組（1）至少存在一個純非復矩陣解的充要條件為，所有解都是純非復矩陣解的充要條件為，由定理2的（10）式可證（19），（20）式成立.

根據本定理的證明思路，還可以得到四元數矩陣方程組（1）其他的特殊解的復分量極秩公式，進一步拓展定理2結論，由于篇幅有限，不再贅述.

3 結語

筆者研究了四元數矩陣方程組（1）的通解中的復矩陣分量的極秩問題.方程（1）有解時，利用復表示φ（·）的相關性質，通過定理1給出與四元數矩陣方程組（1）等價的復矩陣方程組的通解.利用分塊矩陣秩的性質及Gaussian變換，在定理1的基礎上，定理2給出四元數矩陣方程組（1）通解中復矩陣分量的極大、極小秩公式，并與已有結論進行了對比.作為應用，定理3給出四元數矩陣方程組（1）具有特殊解時的極秩公式.文章擴展了已有的四元數矩陣方程（組）通解復分量極秩理論，為該問題的研究提供了參考.