基于PCA-SVM的巖爆預測

劉曉悅，張雪梅，楊 偉

(華北理工大學電氣工程學院，河北 唐山 063000)

巖爆是深部巖體工程開挖中常見的一種動態、自發、不受控制的地質災害。開挖圍巖在高地應力條件下應力場重新分配，導致巖石破裂并產生的一系列不利的影響,如破裂、剝離排出、突然釋放了硬脆性圍巖儲存的彈性應變能量。因為巖爆過程是突發的、強烈的，而且巖石顆粒可以以8～50 m/s的速度噴射出來，威脅地下工作人員和設備的安全，影響作業的進度，進而導致整個工程被阻礙。由于越來越深的開挖和越來越高的應力水平，巖爆的發生越來越頻繁，巖爆問題也日益突出[1]。然而，受模型和參數不確定性影響的巖爆預測分類是一個非常復雜的非線性過程，巖爆分類仍是一個巨大的挑戰。因此，引入一種新的智能方法來研究巖爆和強度分級預測仍然十分必要。

本文通過主成分分析方法對文獻中選取的巖爆預測指標進行分析，解決了數據之間的相關性問題，將提取出的指標用于SVM模型。最后通過支持向量機用于巖爆預測數據的訓練并建立相應的預測模型，有效解決了復雜影響因素情況下模型難以確定的問題，為巖爆預測研究提供了一種新的方法。

1 方 法

1.1 主成分分析(PCA)

主成分分析方法的核心是線性組合原始指標，使之成為一組包含大部分原始信息的獨立的、新的、綜合的指標集。具體步驟如下所述[2-3]。

步驟1：將原始數據進行標準化。假設原始評價指標數據矩陣為X=(xij)m×p，見式(1)。

(1)

標準化處理數據，見式(2)。

(i=1,2,…,m;j=1,2,…,p)

(2)

式中：xj為均值；sj為標準差。

步驟2：計算相關系數矩陣R，即：R=(rkl)m×p(k,l=1,2,…,p)，其中，rkl(rkl=rlk)的計算公式見式(3)。

(3)

步驟3：計算R的特征值λ1,λ2,…,λp和特征值對應的單位化特征向量p1,p2,…,pp。

步驟4：選取主成分數，計算主要成分的累計貢獻率，通常取大于1的特征值且在85%以上的累積貢獻率[4]。

(4)

(5)

式中：vh為第h個主成分的方差貢獻率；vs為前k個主成分的累計貢獻率。

步驟5：計算提取主成分的對應得分。主成分系數矩陣為：U=(p1,p2,…,pp),若從原指標中提取了前k個主成分，則有式(6)。

(s=1,2,…,k)

(6)

1.2 粒子群優化支持向量機理論(PSO-SVM算法)

1.2.1 支持向量機理論

支持向量機(SVM)是在20世紀90年代中期開始發展的一種機器學習方法，是借助于最優化方法解決機器學習的問題的新工具。它通過尋求最小的結構化風險以最小化經驗風險和置信范圍來提高學習機的泛化能力，以便在統計樣本量較小時，可以得到比較好的統計。經過國內外研究者的不斷努力，支持向量機在回歸預測和密度估計中的重要性日益提高，其應用領域也在不斷擴大[5]。其中支持向量機示意圖如圖1所示。

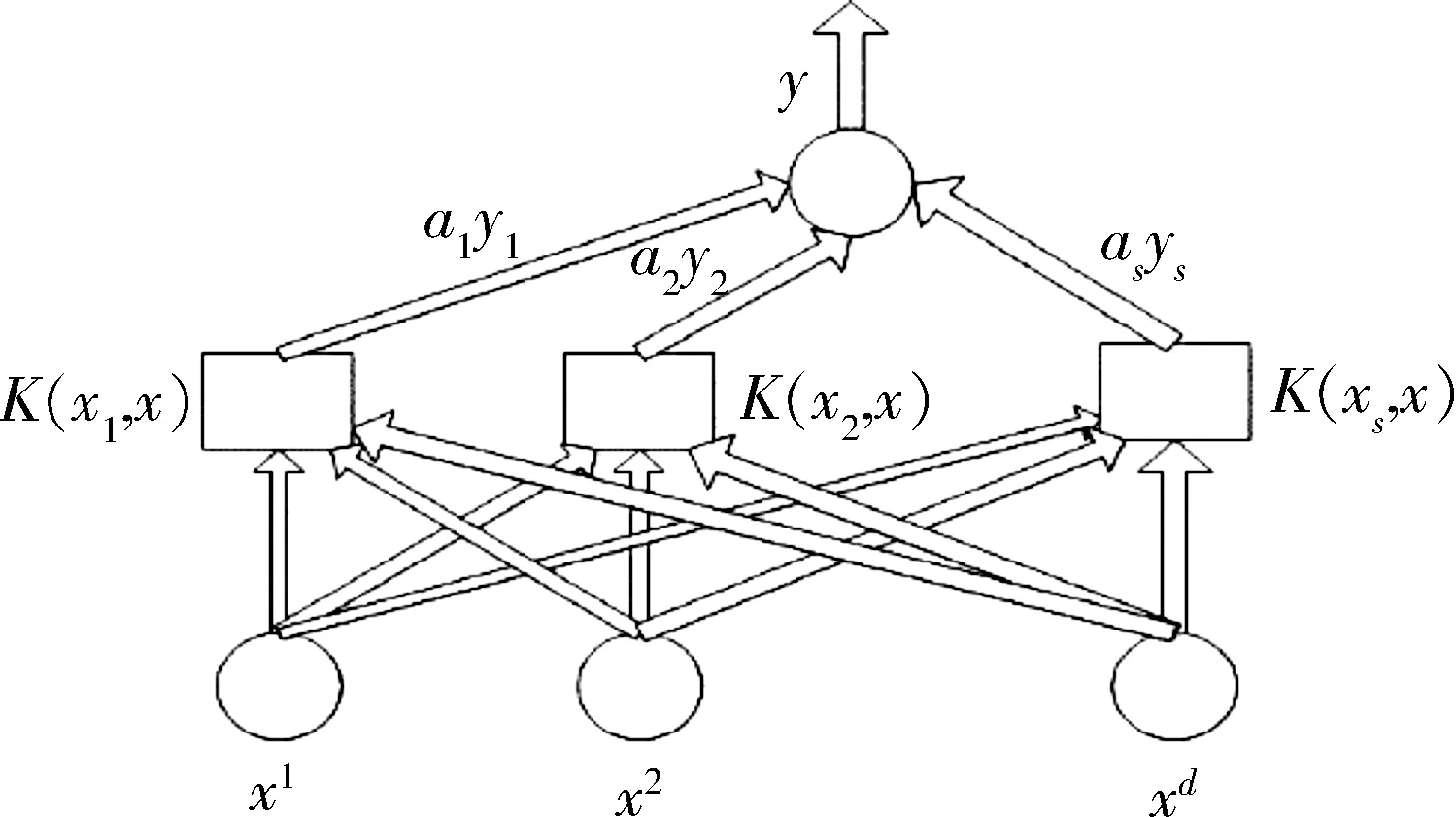
圖1 支持向量機示意圖Fig.1 Support vector machine schematic

1) 線性支持向量機。要想把兩種樣本正確的分開，則需要超平面w×x+b=0。為了保證分類間隔最大，那么優化方法則表示為式(7)。

(7)

拉格朗日函數可用于將原始問題轉換為對偶問題，得到式(8)。

(8)

由式(8)求解之后，得到了最優分類函數，見式(9)。

f(x)=sgn(wTx+b)=

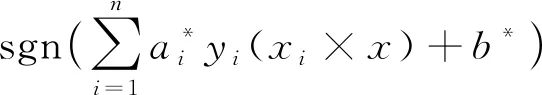
(9)

但是，在實際情況中存在許多線性不可分的情況，因此使用線性可分方法會引起很大的誤差。 應對這種情況，在引入松弛變量后問題就變成了式(10)。

(10)

式中，C為懲罰因子。

引入拉格朗日算法求解該問題，可得到式(11)。

(11)

通過求解各類系數ai后，得到分類決策函數，見式(12)。

(12)

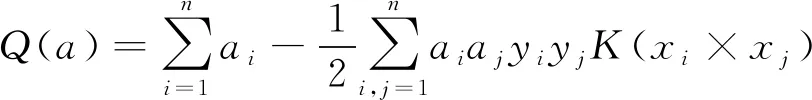
(13)

分類決策函數變為式(14)。

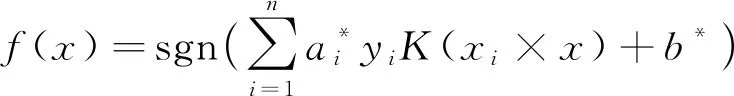
(14)

實際上，映射后仍然不可分的情況也是存在的。

3) 核函數。核函數對于支持向量機的訓練算法具有決定性的作用，常用的核函數有四種：線性核函數、多項式核函數、最常用的徑向基函數(RBF)、Sigmoid核函數。 本文選用最常用的徑向基函數。

1.2.2 基于粒子群算法的支持向量機參數優化

粒子群優化(PSO)是EBERHART等專家提出的基于種群的隨機優化算法。在粒子群算法中，每個優化問題的解決方案都是搜索空間中的一個粒子。在粒子群算法中，每個優化問題的解決方案都是搜索空間中的粒子。所有粒子都具有通過優化函數確定的適應度值，并且每個粒子還具有確定其飛行方向和距離的速度v。 粒子優化算法過程為：①初始化粒子的位置和速度；②計算粒子適應度(本文以訓練樣本的輸出值與實際值的誤差作為適應度函數)；③尋找個體極值和群體極值；④更新位置和速度；⑤計算更新后粒子的適應度；⑥更新個體極值和群體極值。看是否滿足條件，若不能滿足條件，則重復步驟③、步驟④、步驟⑤和步驟⑥，直到滿足條件則可以結束優化過程，得到最終優化后的支持向量機參數。

粒子群優化算法一般需要比較少的調整參數，不僅算法簡單而且容易達到優化目標，適合在動態、多目標環境中尋優。與傳統算法相比，它不僅能夠使計算速度更快，而且能使全面的搜索能力變得更好。因此本文采用粒子群算法去優化支持向量機的參數，這樣才能提高巖爆預測模型的準確性，進而建立性能良好的巖爆預測模型。

2 巖爆預測模型的建立

2.1 選取巖爆預測標準

建立巖爆評價指標體系的原則是評價指標應能反映巖爆的主要特征和圍巖的性質，并能方便地獲取數據，本文選取了6個最具有代表性的指標：圍巖切向應力σθ、單軸抗拉強度σt、單軸抗壓強度σc、應力系數σθ/σc、脆性系數σc/σt以及沖擊傾向性指數Wet。

巖爆烈度等級通常分為四級：Ⅰ級(無巖爆活動)、Ⅱ級(輕度巖爆活動)、Ⅲ級(中度巖爆活動)、Ⅳ級(劇烈巖爆活動)。巖爆等級分類標準見表1[6]。

表1 巖爆等級分類標準表Table 1 Rockburst classification

2.2 PCA預處理

本文通過資料查閱[7]，獲得了30組國內外地下工程實例，訓練樣本數據25組，預測樣本數據5組，對從文獻中查到的巖爆案例原始數據，首先根據標準化公式對數據進行標準化處理，然后將得出的結果進行主成分分析，本文采用Matlab程序對數據進行主成分分析，最終提取出主成分F1、F2和F3。由于篇幅關系無法將數據列出來，因此本文并未將巖爆案例原始數據與主成分數據列出來，但重要分析過程已將列出。各指標間的相關系數和主成分特征值及貢獻率見表2和表3。

表2 相關系數矩陣Table 2 Correlation coefficient matrix

從表3中找出特征值大于1且累計貢獻率在85%以上的前K個主成分,因此本文選取了前3個主成分作為支持向量機模型的輸入。

表3 主成分特征值及貢獻率Table 3 Principal component eigenvalue and contribution rate

表4為主成分載荷(即主成分系數矩陣)，得到3個主成分F1、F2、F3與6個指標變量之間的關系為式(15)～式(17)。

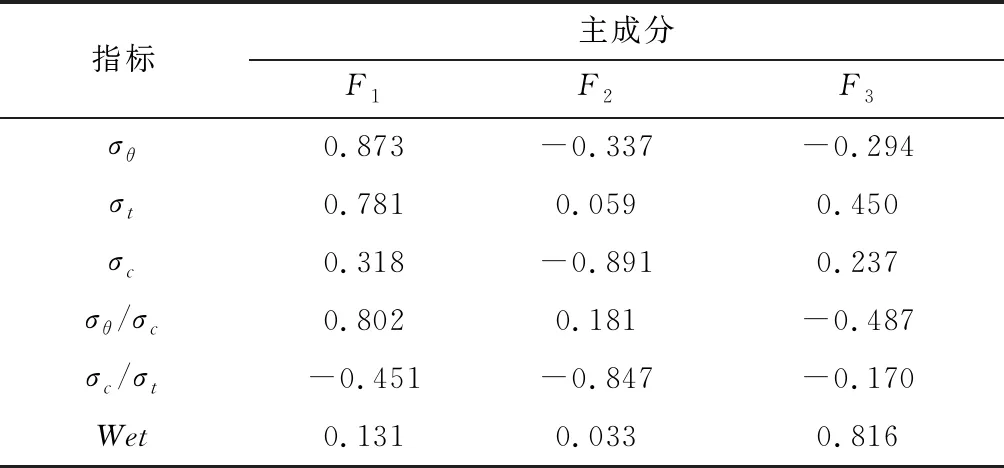
表4 主成分載荷Table 4 Principal component load

F1=0.873x1+0.781x2+0.318x3+

0.802x4-0.451x5+0.131x6

(15)

F2=-0.337x1+0.059x2-0.891x3+

0.181x4-0.847x5+0.033x6

(16)

F3=-0.294x1+0.450x2+0.237x3-

0.487x4-0.170x5+0.816x6

(17)

將標準化之后的指標數據代入式(15)～式(17)，可以得到3個主成分數據綜合指標F1、F2、F3，將三個指標作為支持向量機模型的輸入，消除了冗余數據和因維數不同而造成的影響，有效降低了變量維數與數據之間的相關性，大大提高了模型的運算效率，從而提供了更為合理的解釋。

2.3 預測模型的建立

粒子群優化支持向量機的巖爆預測模型流程圖如圖2所示。

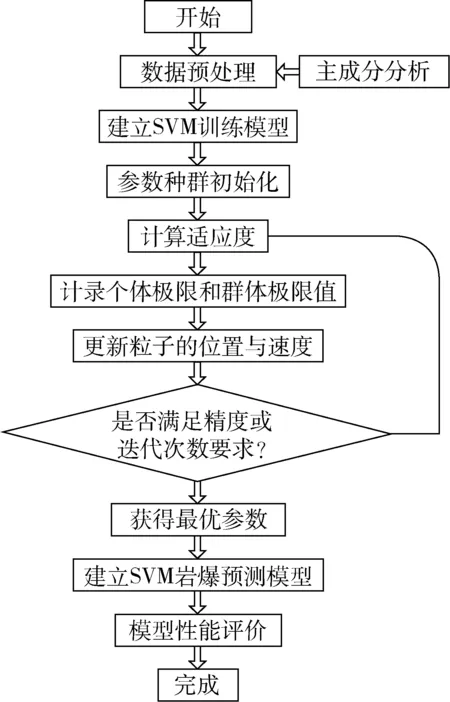
圖2 巖爆預測流程圖Fig.2 Rockburst prediction flowchart

本文為了滿足巖爆預測模型支持向量機(SVM)的精度要求，核函數選擇了徑向基函數，優化懲罰參數c和核函數g選擇了粒子群算法(PSO)。PSO算法的初始化的參數為：加速度C1=1.6，C2=1.5，終止代數=300，種群數N=5，并在多次迭代之后進行優化，最后得到的SVM參數最優值c=9.876，g=2.234，參數優化過程如圖3所示。

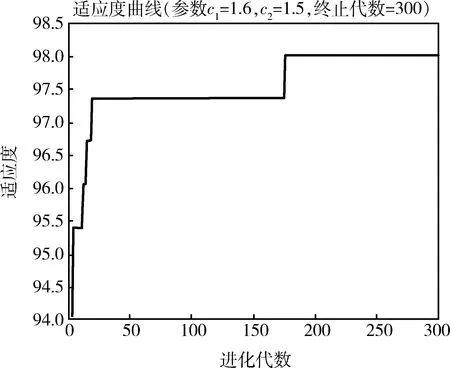
圖3 參數優化的適應度收斂曲線Fig.3 Adaptive curve of parameter optimizaion

上文根據主成分分析對數據進行處理之后，得到主成分F1、F2和F3，因此從樣本數據中隨機抽取25組訓練樣本，剩下的5組作為了預測樣本，由優化之后的預測模型PSOSVM對5組樣本進行預測，得出的預測結果見表5。

由表5可知，選擇5組預測樣本結果與實際預測等級相符，說明本文建立的PCA-PSOSVM巖爆預測模型具有一定的可行性。

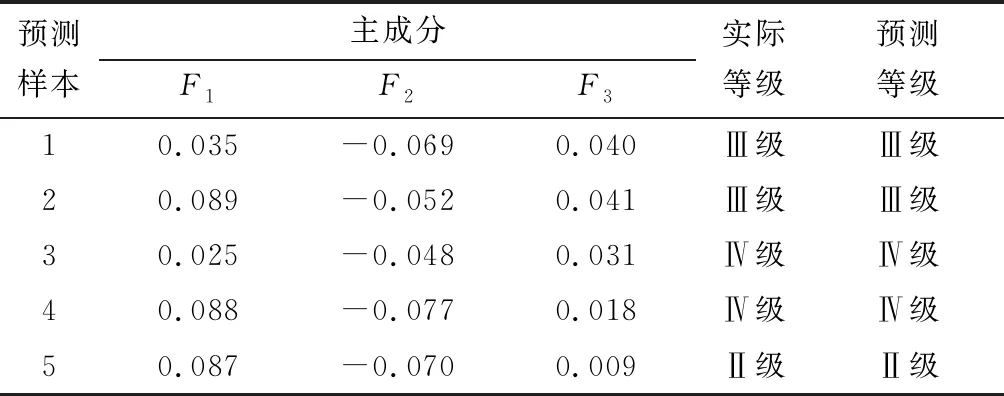
表5 PCA-PSOSVM模型巖爆預測等級Table 5 PCA-PSOSVM model rockburst prediction level

2.4 不同模型比較

為了進一步驗證巖爆預測模型PCA-PSOSVM模型的準確性，必須與不同的巖爆預測模型對同樣的巖爆數據進行預測，因此本文進行了不同模型的對比。其中，表6當中其他模型的預測結果數據選自文獻[8]，比較以上三種模型對11個測試樣本的測試結果，發現三種模型預測正確率分別為90.9%、 72.7%和81.8%， 說明PCA-PSOSVM模型相對于SVM模型和ANN模型而言，具有更高的準確率，因此PCA-PSOSVM模型具有一定的可行性。

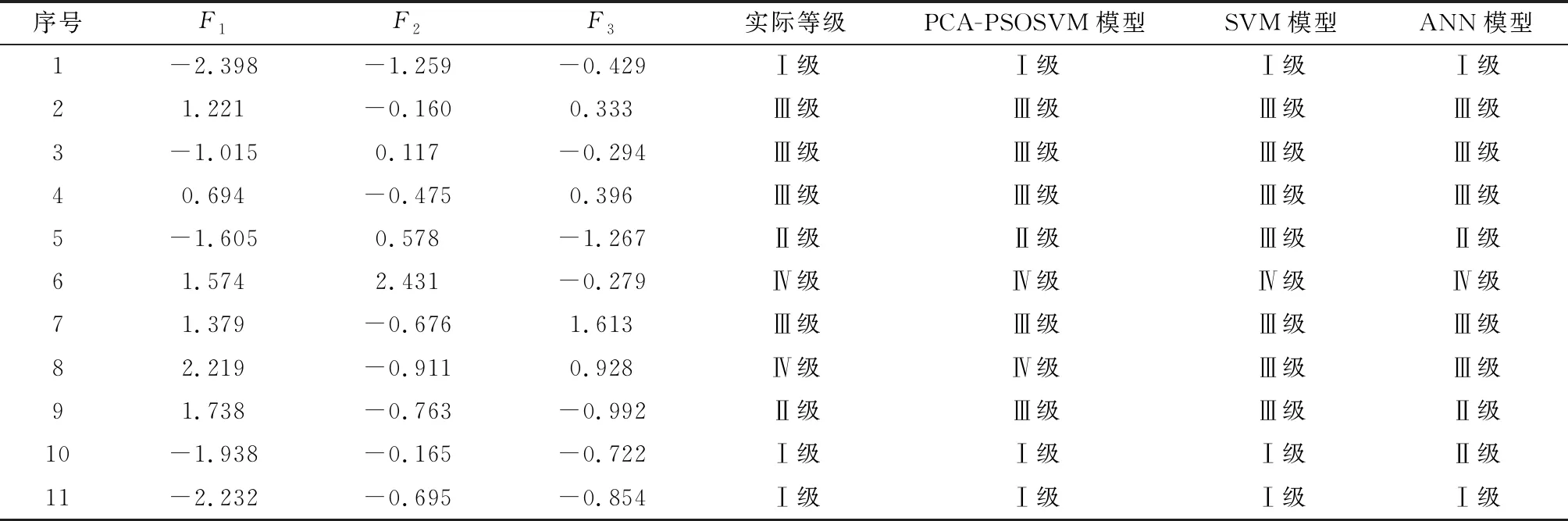
表6 不同預測模型預測結果對比Table 6 Comparison of prediction results of different prediction models

3 結 論

1) 選用主成分分析對原始數據處理，可以消除指標間的相關性，并選出3個主成分達到了降維的目的，這樣支持向量機的模型輸入就會變成3個，大大簡化了計算過程。

2) 對SVM模型來說，對模型性能影響較大的是懲罰參數c和核函數g，所以本文使用粒子群算法(PSO)去優化懲罰參數c和核函數g，這樣一來就提高了SVM巖爆預測模型的準確性。

3) 為了驗證準確性，用本文建立的PCA-PSOSVM模型與支持向量機(SVM)模型和人工神經網絡(ANN)模型的預測結果進行對比，發現PCA-PSOSVM模型具有更高的巖爆預測準確率。