面向關鍵鏈識別的礦山項目進度優化與仿真

蔣淑云，侯 杰，李國清，陳連韞，莫 偉

(1.北京科技大學土木與資源工程學院，北京 100083； 2.山東黃金集團有限公司，山東 濟南 250101)

進度管理是礦山項目管理中重要一環，合理地進行項目進度管理，不僅能保證項目按時完成，控制項目成本，達到利益最大化，而且可以保證項目建設質量并提高效率，避免不必要的錯誤。礦山項目建設具有影響因素多、建設周期長、人財物消耗多等特點[1]，如何衡量進度、成本與質量三者間的關系，是礦山項目進度管理的一個難題。

當前我國企業常用的進度管理方法是關鍵路徑法(critical path method，CPM)、塔接網絡計劃法和計劃評審技術(program evaluation and review technique，PERT)，但由于這些方法只考慮邏輯關系，未考慮在項目實施過程中的資源約束和人的行為因素影響，導致大部分項目存在開發周期延誤和成本超支情況，因此很多學者開始了進度優化方面的研究。汪勇等[2]通過基于活動績效的掙值法分析了項目質量對成本、進度的影響，為項目控制提供一種計算方法，適用于大型復雜項目管理工作；馬國豐等[3]針對目前進度管理塔接技術研究中的局限性，提出改進的塔接進度-成本算法與分析方法，實現塔接活動的精細化；歐陽業偉等[4]通過將3D建筑信息模型與進度計劃鏈接，實現了對施工過程的模擬與直觀形象的進度表達方式；倪永等[5]綜合考慮時間與資源雙重約束，采用關鍵鏈法進行項目進度管理等。

上述方法在項目進度管理方面均取得一些成效，其中基于約束理論的關鍵鏈法[6]通過時間參數與資源約束情況確定關鍵鏈，并通過在非關鍵鏈設置緩沖區，減少項目中不確定性所帶來的影響，提高資源利用率，減少工期的逾期[7]，并快捷有效地進行進度管理。本文基于關鍵鏈技術，采用灰色關聯來確定子任務的優先準則，綜合資源約束與成本的關系，可得出最優進度計劃。

1 礦山工程項目進度管理特點

1) 礦山工程施工具有明確順序，但易受地下空間與工作面的影響，導致進度難以控制，增加進度管理難度。

2) 礦山項目通常是大型綜合建設項目，具有建設周期長、組織關系復雜、資源需求特殊、不可逆轉性等特點，包括人為因素在內的不可預見因素均可能影響項目建設，因此，必須實時調節項目進度，保證項目按時完成。

3) 礦山工程項目由于施工環境、工藝與機械水平等導致不可預見的因素較一般建設項目多，項目工期不易控制。

4) 礦山項目由于所需資源種類多、資源消耗量大且工序復雜、工作量大，導致項目建設過程中約束較大，對項目進度的影響較大。

2 項目進度管理模型構建

2.1 工作分解結構(work breakdown structure，WBS)

根據項目相關資料識別可交付成果或中間輸出，確定項目工作分解結構的類型，再依據分解原則與步驟，結合項目團隊責任體系，將項目分解成具體活動，并繪制WBS的層次結構圖。

2.2 關鍵鏈識別

關鍵鏈的識別過程與項目調度過程相似，其核心在于對資源約束的分析。啟發式算法是當前資源受限項目調度(resource constraint project scheduling problem，RCPSP)求解算法中使用率最高的算法，通過指定優先規則并識別瓶頸因素來確定關鍵鏈[8]。

平行啟發式算法常用優先準則有十幾種，主要考慮某一時段及該時段內能夠安排的所有子任務，但由于項目中存在多種資源約束、項目工序復雜交替且數量多、工序持續時間長短不一，可考慮綜合采用多種優先準則，利用灰色關聯算法計算工序關聯度，根據工序關聯度從大到小排序。

本文基于多資源約束的任務優先調整原則考慮子任務的資源影響度、子任務持續時間與子任務的緊后任務持續時間，并采用灰色關聯度分析法綜合以上三個影響因素，以此確定子任務的調整優先級。灰色關聯度系數ξi(k)的公式見式(1)。

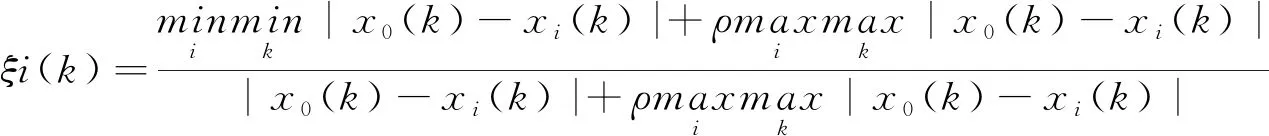
(1)

關鍵鏈識別流程如下所述。圖1中，S1與S2具有相同的工序邏輯關系，S1表示以子任務最早開始時間為開始時間編制的進度計劃，S2表示以子任務最晚開始時間為開始時間所編制的進度計劃。

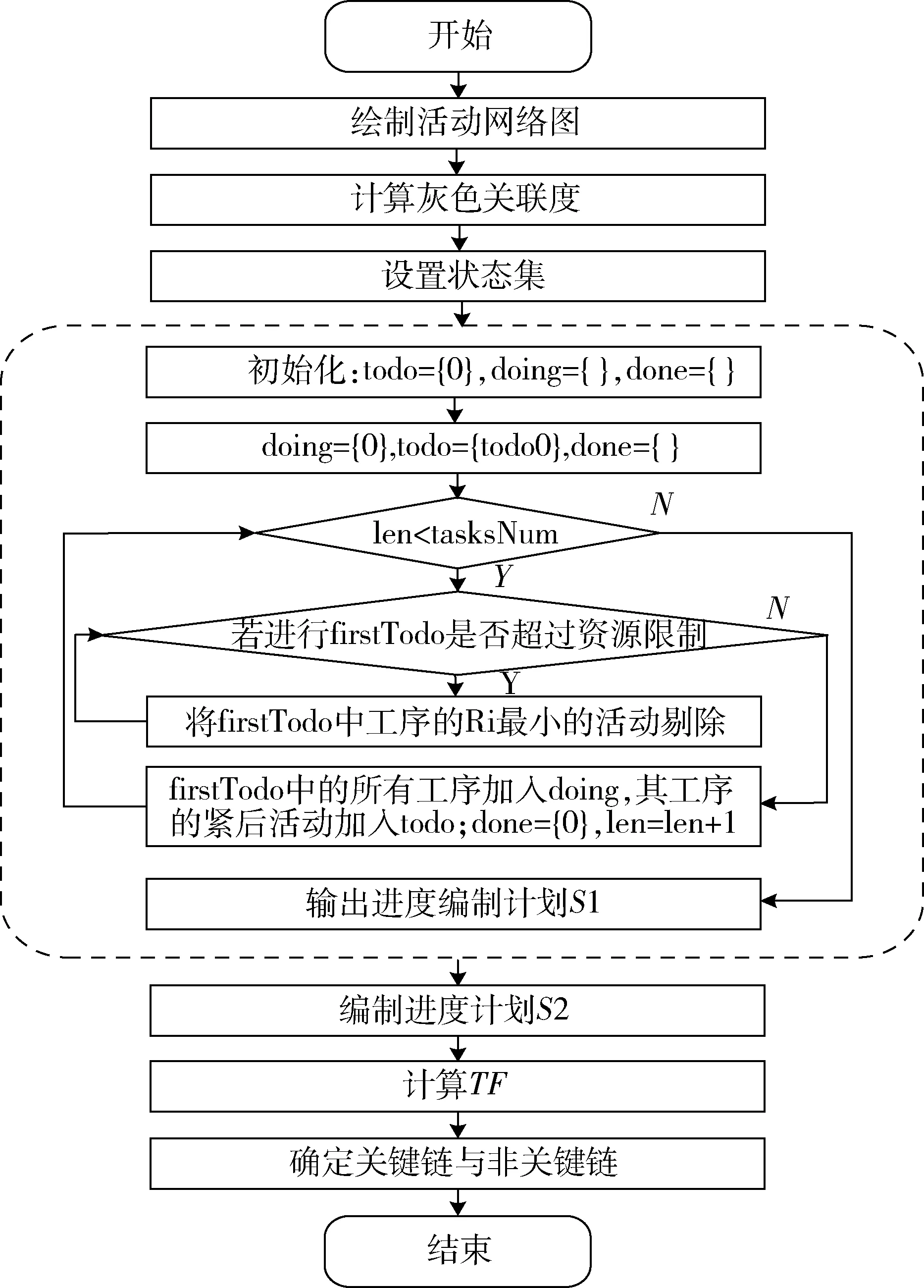
圖1 關鍵鏈識別流程圖Fig.1 Flow chart of critical chain identification

1) 繪制活動網絡圖。確定子任務間的緊后邏輯關系與子任務的資源需求量，增加虛擬子任務0在計劃的開始，繪制子任務網絡圖。

2) 計算灰色關聯度。計算所有子任務工期、資源影響度、緊后子任務持續時間，計算所有子任務的灰色關聯度Ri。

3) 設置狀態集。設置狀態集doing={正在進行的子任務}、todo={將要進行的子任務}、done={已完成的子任務}；子任務個數為tasksNum，done中元素的個數為len，todo中所有緊前活動已完成的子任務集合為firstTodo。在每一次迭代中，項目各子任務分別處于doing、done、todo狀態集。

4) 編制進度計劃S1。根據動網絡圖與本文設定的優先規則，以子任務的最早開始時間為開始時間，編制進度計劃S1。

①首先，子任務狀態初始化。虛擬子任務0處于候選狀態集，即0∈todo;子任務的緊后子任務集為Ai,所有子任務集為M。②開始第一次循環，首子任務0∈doing；首子任務的緊后子任務則進入候選集，即A0∈todo。③進入第二次循環，首子任務0執行完成進入已完成狀態集，即0∈done。判斷當前done的長度是否小于工序個數，若小于，則從todo中選擇所有緊前活動已完成的子任務為集合firstTodo，轉向步驟④；否則直接輸出進度計劃S1，轉向步驟5)。④判斷若doing中加入firstTodo是否會超出資源限制，若超出，則選擇關聯度最小的子任務，將其從firstTodo中刪除；否則，firstTodo中的所有元素進入doing，其緊后工序進入todo，len=len+1，轉向步驟③。

5) 編制進度計劃S2。在進度計劃S1的基礎上，以最晚結束時間為結束時間，從倒數第二個子任務開始從后向前安排，同時滿足資源約束，生成進度計劃S2，S2為最終的調度計劃。

6) 計算TF。計算S1與S2中所有子任務的最早開始時間與最晚開始時間的差TF，若TF=0，則該子任務處于關鍵鏈上，否則該子任務處于非關鍵鏈上。

7) 確定關鍵鏈與非關鍵鏈。若關鍵鏈有多條，則選取一條關鍵鏈上所有子任務持續時間最長的為關鍵鏈，其余為非關鍵鏈。

2.3 緩沖區設置

緩沖區設置的影響因素[9]如下所述。

1) 項目經理風險偏好α。項目管理者會根據項目評估與自身風險偏好，選擇不同的項目按期完工保證率。則風險水平下的緩沖調整系數為：β=f1-α/2。

2) 網絡復雜度δ。δ=(Np+1)/N，表示子任務的緊前子任務數與該子任務所經鏈路上的總子任務數的最大值的比值。

3) 資源緊張度λk。出于控制成本與將資源統一度量的目的，在綜合考慮工期與成本的情況下,資源緊張度的計算公式見式(2)。

(2)

4) 安全時間Δt。項目中子任務的持續時間服從均值和方差的正態分布，取2倍的標準差為子任務的安全時間，則Δt=2σ。項目的緩沖區計算公式見式(3)。

(3)

3 實例分析

3.1 案例描述

以山東某礦山的選廠項目為例，研究該進度優化模型在礦山領域的應用方法。礦山為尋求企業經濟效益最佳化、穩定并優化選礦生產指標等效果，該項目結合礦山實際情況,利用智能制造與現代信息化手段,全力建造“設備自動化、人員高效化、管理信息化”的智能選廠。為縮短項目工期，盡早投入生產，礦山將選廠基礎建設與智能建設同時進行。智能選廠通過建設數據采集平臺、智能操作選廠、虛擬選廠及云服務系統，實現選礦工藝過程、工藝參數自動調節與控制、數據的集中管理與應用，提高選廠的智能化操作程度，從而穩定和優化流程，減員增效，提高技術和經濟指標。

該項目經WBS分解后共有29道工序，其所需資源種類有6種(R1至R6)，項目工期估算方法采用PERT，再根據最樂觀時間o、最可能工期m、最悲觀工期p計算子任務的期望工期，具體相關數據見表1。

表1 任務邏輯關系與持續時間Table 1 Task logic relationship and duration

圖2 項目網絡圖Fig.2 Project network diagram

3.2 關鍵鏈確認與緩沖區計算

3.2.1 計算子任務灰色關聯度

首先，根據項目網絡圖與WBS分解表，確定編號為1的子任務為參考數列；其次，設置資源限制量，計算子任務的資源影響度、持續時間與緊后子任務持續時間，并將所有變量無量綱化，增加數據的有效性；計算比較數列與參考數列的差值，分辨系數ρ取0.5，計算子任務關聯系數；最后計算子任務的灰色關聯度，即關聯系數的均值。

3.2.2 確定最佳資源限制量

設置不同的資源限制量組，根據子任務的灰色關聯度、工期與資源需求量，進行項目計劃編制，并得出項目工期。

由表3可知，成本較低的方案為方案6和方案12，但方案12的工期較方案6延長101 d，不滿足項目建設需求，因此方案6為最優方案，此時的資源限制量為{R1=2,R2=1,R3=9,R4=6,R5=9,R6=3}，項目工期為525 d。

表3 資源限制量與工期、成本的模型Table 3 Model of resource constraints,construction and cost

3.2.3 識別關鍵鏈

在方案6的進度計劃S1基礎上，以最晚結束時間為結束時間，從倒數第二個子任務開始從后向前安排，同時滿足資源約束，生成進度計劃S2。

計算S1與S2兩個計劃中所有子任務的時差TF，此時TF=0的子任務有{1,2,16,17,18,19,29}。 由此得出項目的關鍵鏈為1→2→16→17→18→19→29。

3.2.4 設置緩沖

項目緩沖(primary buffer，PB)通常設置在關鍵鏈的結尾，防止項目出現逾期；匯入緩沖(filter buffer，FB)設置在非關鍵鏈和關鍵鏈的結合處，避免非關鍵鏈對關鍵鏈的進度產生影響。該進度計劃的緩沖設置如圖3所示。

表2 資源單價Table 2 Unit price of resources

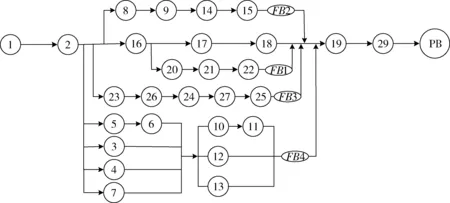
圖3 項目關鍵鏈及緩沖設置Fig.3 Project critical chains and buffer settings

在項目完工保證率為95%的情況下，風險緩沖調整系數為β=f0.95/2=0.825。通過計算得出的結果見表4。

表4 項目緩沖影響因素值Table 4 Value of the project buffer impact factor

結合表4中的信息，項目緩沖可通過式(3)計算得出，則PB=5.99，同理可得，由子任務{1,2,16,20,21,22}到關鍵鏈的匯入緩沖FB1=5.48，由子任務{1,2,8,9,14,15}到關鍵鏈的FB2=4.55，由子任務{1,2,23,26,24,27,25}到關鍵鏈的FB3=5.76，由子任務{1,2,5,6,10,11}到關鍵鏈的FB4=4.22。加入緩沖后的項目總工期為533.54 d。

3.3 結果分析

分別采用剪切-粘貼法[10]、根方差法[11]、朱建信[12]、孟憲寬等[13]提出的方法計算本文案例的緩沖區與項目總工期，作為對照組，驗證本文緩沖設置方法的優越性。四種方法通過計算得出的緩沖依次為{PB=9.5,FB1=9.75,FB2=8.25,FB3=11.25,FB4=8.25}、{PB=7.25,FB1=8.05,FB2=6.84,FB3=8.62,FB4=6.84}、{PB=6.10,FB1=5.69,FB2=4.56,FB3=5.76,FB4=4.23}、{PB=13.78,FB1=16.94,FB2=13.08,FB3=18.03,FB4=12.45}，則此時的項目總工期依次為540.75 d、537.09 d、533.66 d、549.86 d。通過數據對比綜合分析可知，本文選用的項目緩沖設置方法在同樣具有保護關鍵鏈順利進行的作用下緩沖區相對最小，可得出該方法優于其他緩沖設置方法，能夠大幅提升管理效率。

由于項目工期具有不確定性，本文采用蒙特卡洛技術對項目所有可能最終完工路徑進行模擬。此時，蒙特卡洛仿真是通過在Excel中建立進度模型，將各工序的工期設為假設單元并服從正態分布，項目總工期設定為預測單元。設置試驗次數為1 000次，得到的模擬結果表示：在考慮到項目建設過程中人為因素等不確定因素影響，按照95%的保證率來估算工期可得項目的期望工期為528 d，項目工期在520 d到536 d的完成概率為95%，而通過計算得出的項目工期533.54 d在95%保證完工率時的工期范圍內，表示根據本文進度優化模型所得出的項目總工期具有很高的可靠度。

通過進度優化模型在項目中的實際應用，該項目在進度管控方面取得了較好的效果，在按時完成項目建設任務的同時節約了8.5%的項目建設成本，極大地提高了生產效率與經濟效益。在項目具有多種資源約束且項目工序結構復雜的情況下，基于關鍵鏈識別的進度優化模型所得出的進度編制既能順利完成項目建設又能節約項目成本，可為同類問題的進度優化提供借鑒意義。

4 結 論

1) 本文的關鍵鏈識別，采用灰色關聯方法，綜合考慮了最多的直接緊后活動準則、最長的活動時間、最大資源需求量準則等幾種平行法啟發式準則，能夠客觀地確定調整的優先級，解決資源沖突。

2) 緩沖區的構建，壓縮了安全時間，有效地解決項目工期過長、資源沖突、進度延期等問題，可明顯提高項目團隊的經濟效益與社會效益。

3) 改進后的工期確定方法按照數學模型生成，尋找到使項目總工期最短與資源利用率最大的最優組合，其方法更為科學合理。