帶花紋輪胎仿真模型建立及影響因素研究

姜洪旭，王海艷，劉昌波

[1.浦林成山（青島）工業研究設計有限公司，山東 青島 266011；2.浦林成山（山東）輪胎有限公司，山東 榮成 264300]

自20世紀70年代有限元方法開始在輪胎設計中得到廣泛應用[1]，但由于花紋結構的復雜性和計算機能力的限制，長期以來輪胎仿真沒能將胎面花紋考慮進去，直到2000年才出現有關帶花紋輪胎抗濕滑性能的仿真研究[2]，之后出現了涉及輪胎六分力、雪地性能和耐磨性能的仿真研究[3-5]。

國內研究人員采用子模型和組合模型技術實現了輪胎花紋靜負荷接地性能仿真，其仿真結果與試驗結果十分接近，并在此基礎上開展了輪胎花紋對輪胎內部受力以及帶花紋輪胎的穩態滾動和顯示滾動的研究[6-7]。由于輪胎花紋結構復雜，使得原來就很復雜的輪胎有限元仿真更加困難，自從Meschke和Shiraishi使用組合模型技術（即將花紋與輪胎其他部分分開建模，如圖1所示）以來，該技術一直沿用至今。

有限元網格質量關系到模型的收斂性和計算精度，獲得較高的網格質量是輪胎花紋有限元建模的一個挑戰。目前主要有兩種輪胎花紋有限元建模方法。一種是基于映射和拉伸，將網格劃分好的花紋展開圖通過坐標變換得到輪胎花紋有限元分析模型。其優點是網格質量能得到保證，建模效率較高，缺點是花紋模型有些失真。另一種是應用CATIA和UG等三維造型軟件完成輪胎花紋幾何建模，然后用Hypermesh進行網格劃分。其優點是可以保證花紋幾何形狀的真實性，缺點是過程比較繁瑣。本工作采用第2種建模方法研究帶花紋輪胎的仿真建模。

1 花紋模型建立

Abaqus帶花紋輪胎建模有兩種方法：一種是建立完整的花紋模型和完整的輪胎其他部分模型，然后將兩者組合生成完整模型（如圖2所示）；另一種是建立單節花紋塊和對應的輪胎其他部位模型，將兩者組合，再沿圓周方向拓展生成完整模型（如圖3所示）。兩種建模方法在幾何結構上可以做到完全一樣，因此對于接地印痕分析，兩者不會有任何差異。本研究采用后一種方法實現帶花紋輪胎的穩態滾動分析。

圖2 建立完整花紋組合式輪胎模型示意

圖3 建立單節花紋組合式輪胎模型示意

Abaqus穩態滾動分析采用的是拉格朗日-歐拉混合描述。拉格郎日描述是指單元節點與材料固定在一起，網格隨著材料運動而變形；歐拉描述是指網格幾何形狀固定而材料在網格內部運動。在Abaqus中輪胎的穩態滾動是通過材料在網格內部的流動來模擬，歐拉描述的要求是材料流動的流線必須是連續的，而考慮花紋時，由于橫向花紋溝的存在，流線被破壞，無法完成滾動的模擬，解決這個問題的方法是建立周期性的模型[8-9]。

輪胎花紋幾何模型根據我公司T116A花紋圖在CATIA中完成建模，如圖4所示。

圖4 輪胎花紋在CATIA中建模示意

輪胎花紋的3D模型建立基本與模具一致，但基于保證后續網格的質量，以利于計算時的收斂性和提高建模、計算效率，仍對花紋結構進行某些簡化處理，如忽略了鋼片、變溝深設計等。為了獲得較高求解精度和網格質量較好的六面體網格，花紋網格的劃分在Hypermesh中完成，見圖5。

圖5 輪胎花紋網格示意

2 模型驗證

2.1 接地印痕

輪胎接地印痕仿真和測試結果見圖6。

圖6 輪胎接地印痕仿真和測試結果

由圖6可以看出，帶花紋輪胎的仿真接地印痕形狀與實測形狀接近，仿真準確度很高。

2.2 穩態滾動仿真的合理性驗證

Abaqus-Standard求解非線性問題采用牛頓-拉普森法求解平衡方程，在分析過程中，將負荷分解成很多小的增量，每個增量的施加過程都需求解平衡方程，以達到穩定狀態。因此，輪胎側偏、側傾的穩態仿真的過程是一個穩態過程，這樣就可以運用汽車動力學中車輪穩態滾動卡姆圓公式來驗證仿真結果是否合理[10]。

車輪穩態滾動卡姆圓公式如下：

式中，Fx為輪胎縱向力，Fy為輪胎側向力，μ為輪胎附著因數，Fz為負荷。

根據上述公式可得到穩態滾動縱向力與側向力的關系。當輪胎穩態滾動時，縱向力的增大會帶來側向力的減小，仿真結果見圖7，其與理論預測趨勢一致，說明仿真結果具有合理性。

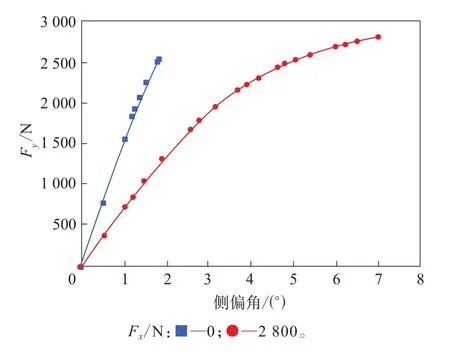
圖7 輪胎穩態滾動側向力與縱向力的關系

3 仿真結果分析

汽車動力學中，關于側向力-側偏角特性都是適用于穩態的，即考察特性曲線時，側偏角是確定的，不隨時間變化，否則側偏特性關系將不再成立。輪胎側偏測試分為穩態測試和瞬態測試，穩態測試是為了匹配車輛懸架，滿足操縱性能的要求；瞬態測試是為了了解極限情況下輪胎性能的可靠性，例如通用汽車公司對輪胎力和力矩的測量就是穩態測量。

本研究通過輪胎的穩態滾動仿真，確定輪胎自由滾動狀態后，對輪胎施加側偏角和側傾角，從而獲得動態接地印痕和六分力特性曲線。

3.1 動態接地印痕

在輪胎達到自由滾動狀態后，給輪胎施加側偏角得到的動態接地印痕如圖8所示。仿真與試驗結果具有相同的趨勢，即隨著側偏角的增大，接地印痕一側接地壓力和接地長度增大。

圖8 輪胎不同側偏角下的動態接地印痕

3.2 花紋對輪胎側偏和側傾特性曲線的影響

花紋對輪胎側向力和回正剛度的影響分別如圖9和10所示。

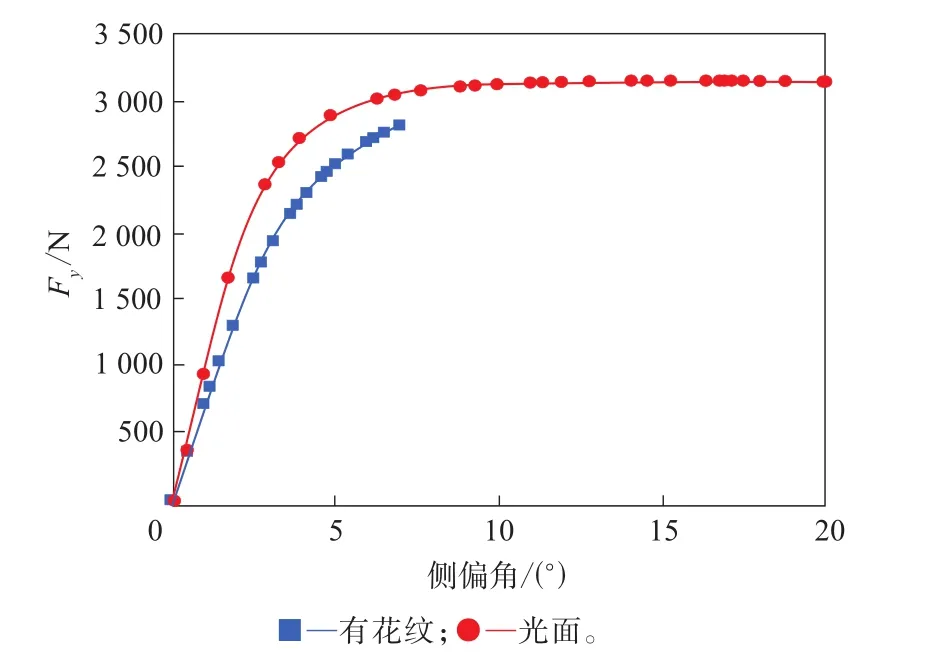
圖9 花紋對輪胎側向力的影響

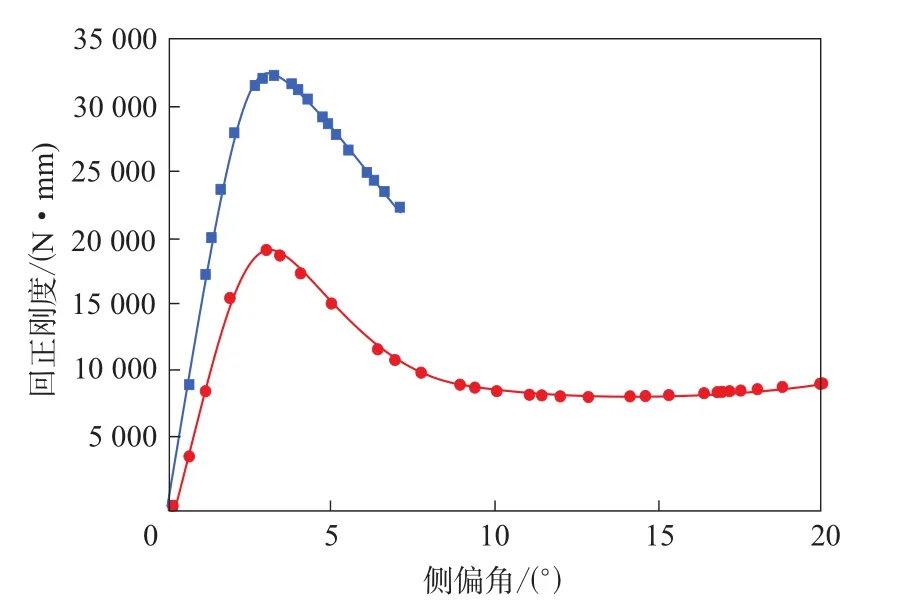
圖10 花紋對輪胎回正剛度的影響

由圖9和10可見，花紋對輪胎側偏和側傾特性影響明顯，考慮花紋后，側向力相比光面輪胎減小，回正剛度則增大。

3.3 路面對輪胎側偏和側傾特性曲線的影響

輪胎的六分力試驗機分為轉鼓式和履帶式兩種，見圖11。本研究通過仿真分析對比兩種路面對輪胎六分力的影響，在Abaqus中建立直徑為1.7 m的轉鼓和平直路面，將兩者均設為剛體，如圖12所示。路面對輪胎側偏和側傾特性曲線的影響如圖13—16所示。

圖11 六分力試驗機

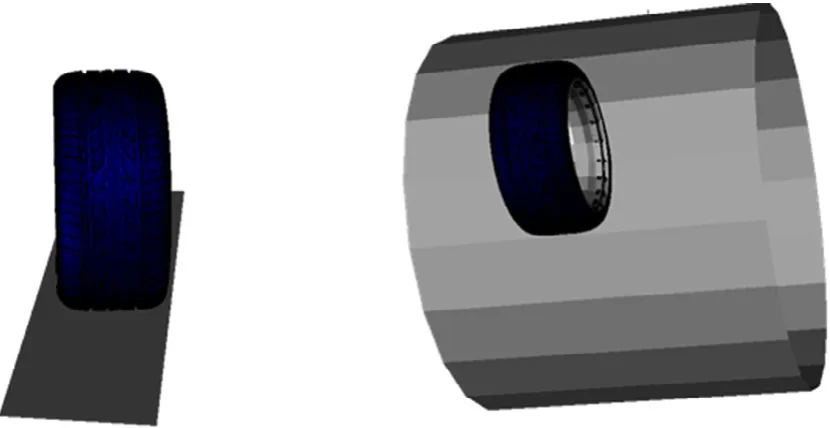
圖12 兩種仿真路面

圖13 路面對輪胎側向力-側偏角曲線的影響

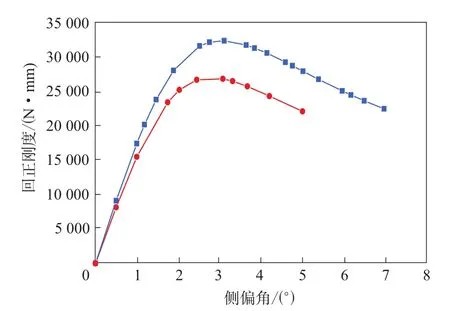
圖14 路面對輪胎回正剛度-側傾角曲線的影響

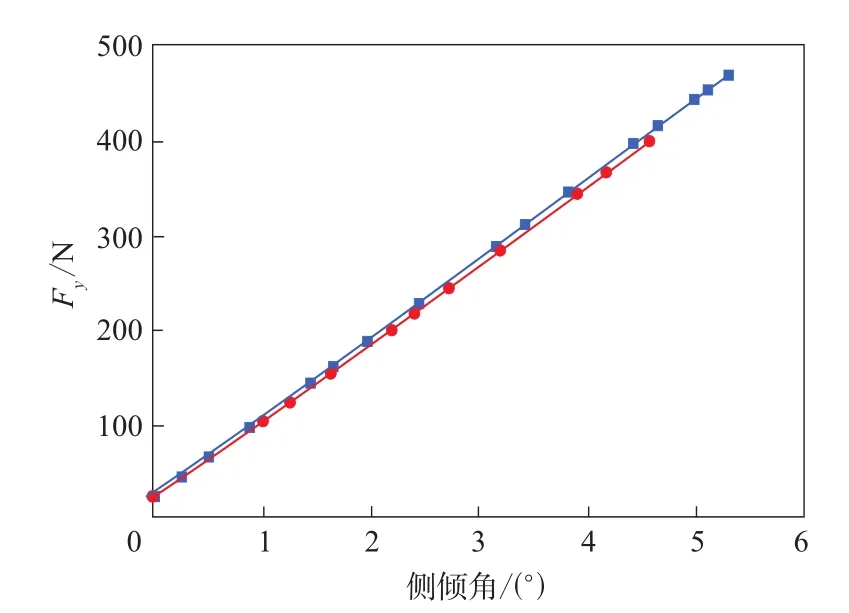
圖15 路面對輪胎側向力-側傾角曲線的影響

圖16 路面對輪胎回正剛度-側傾角曲線的影響

由圖13—16可知：轉鼓和平直路面的側偏特性曲線幾乎沒有差異，而回正特性曲線則明顯不同，平直路面上的回正剛度和最大回正力矩大于轉鼓路面；側傾特性曲線也有相同規律，側向力在平直路面和轉鼓路面上相差不大，側傾力矩在平直路面上要明顯大于在轉鼓路面上。

3.4 輪胎力和力矩穩態測試項目仿真

根據通用汽車公司輪胎力和力矩測試項目[11]，采用有限元仿真得到六分力曲線進而處理得到其要求的數據，輪胎規格為225/40R18。

轉向因數（μc）計算公式如下：

側偏角為1°時，μc＝2 152.74/6 300＝0.34。

回正剛度因數（μA）計算公式如下：

式中，MA為回正力矩。

側偏角為1°時，μA＝61 948.1/6 300＝9.83。

負荷靈敏度函數（H）計算公式如下：

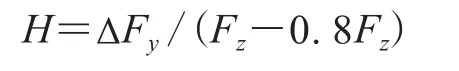
側偏角為1°時，H＝（2 152.74－1 916.84）/1 260＝0.187。

負荷傳遞靈敏度函數（G）計算公式如下：

式中，P為負荷，α為側偏角。

當側偏角為4°時

4 結論

（1）帶花紋輪胎仿真模塊靜負荷接地印痕精度達到90%以上，接地印痕仿真結果與實測結果十分接近。

（2）完成了帶花紋輪胎靜負荷接地印痕、穩態滾動、穩態側偏和側傾仿真功能開發，可獲得帶花紋輪胎六分力曲線，預測動態接地印痕。