渦流場中波動魚形體推進特性數值模擬

李永成，陳紀軍，閆 朋

（中國船舶科學研究中心，江蘇 無錫 214082）

0 引 言

自然界中的魚類經過長時間的進化之后已具備非凡的運動能力，其運動方式主要分為鰻鱺模式、鲹蝌模式和月牙尾推進模式等3種。在鲹蝌模式和月牙尾推進模式中，魚類僅部分身體參與擺動，其余部位保持剛性，典型代表有鯨魚等。這2種運動方式可抽象為拍動運動，通常用耦合的升沉運動和俯仰振蕩運動代替。在鰻鱺模式中，魚類全身作橫向擺動，以行波方式向前運動，典型代表有鰻魚等。這種運動方式可抽象為魚形體波動運動，在理論分析或數值計算中，通常用平板或對稱翼型代替魚身，沿身長方向的各點作橫向振動。對于橫向振動的具體運動形式，一種較為常用的描述方式是平板或對稱翼沿身長方向作行波運動，身長方向上各點的橫向位移可通過正弦函數或余弦函數表示。

國內外已有很多學者對魚形體波動推進進行研究。

1) 在理論研究方面：LIGHTHILL提出了細長體理論，用以求解波動魚形體的受力問題；WU提出了三維波動板理論，成功地解決了無黏流場中三維波動魚形體的數值計算問題；CHENG等提出了半解析半數值的渦格法，該方法已成功應用于三維波動魚形體流場模擬中。

2) 在試驗研究方面：BARRETT等通過研制仿生波動機器魚，證實了與相同尺寸的剛性魚相比，波動機器魚達到相同航行姿態耗費的能量更少；LAUDER應用DPIV（Digital Particle Image Velocimetry）研究了波動魚形體長鰭的漩渦尾跡與尾鰭的漩渦尾跡的相互影響，結果表明，長鰭與尾鰭相互作用的水動力學效應可使魚形體的推進力得到增強；KATO對低速條件下魚形體波動運動特性進行了分析，其研制的第四代樣機具有良好的操作性。

3) 在數值計算方面：EPSTEIN等采用RANS方法將魚形體簡化為正弦行波運動，獲得了其推力與行波運動參數之間的關系；RAHMAN等以烏賊為仿生對象，將波動鰭簡化為等擺幅波動的矩形鰭面，采用基于泊松方程控制生成的體貼動網格，計算得到了鰭面上的壓力分布特征；潘定一等和LI等采用浸沒邊界法對二維波動、三維波動和形體進行了低雷諾數下的直接數值模擬研究，確立了最佳運動參數。

在上述關于魚形體波動的研究中，一般將魚形體置于均勻來流或靜止流體中，流場可認為是穩態流場。然而，在真實的自然界中存在著各種障礙物（如珊瑚和礁石等），流場中存在著各種漩渦魚形體，其周圍的流場通常較為復雜。鑒于此，本文主要研究渦流場（非穩態流場）中波動魚形體的推進特性。通過在魚形體上布置一個靜止方柱模擬非穩態流場，系統分析靜止方柱與魚形體之間的距離和斯特哈爾數對波動魚形體推進特性的影響，為以后小型仿生潛器研制提供參考。

1 計算模型

圖1為物理模型示意。計算模型為二維NACA0012剖面翼型，弦長為

C

，與一個方柱前后串聯布置，翼型頂端與方柱后端之間的距離為

S

，方柱的邊長為

a

。選取一個矩形計算域，來流從左至右依次流過方柱和魚形體，以翼型弦長為特征長度，整個計算域的范圍在流向上為26倍弦長，在垂直方向上為16倍弦長。關于邊界條件設置，除了將計算域右側設為壓力出口邊界條件，計算域其他邊界均設為速度入口邊界條件。

圖1 物理模型示意

魚形體的頭部被固定，身體的其他部分作行波運動，變形起始位置與魚形體頭部之間的距離為0.3

C

。對于作行波運動的魚形體而言，其橫向位移的表達式為

式(1)和式(2)中：

A

(

x

)為幅值函數；

a

、

a

和

a

為用于控制魚形體的波動幅值，根據參考文獻的建議，

a

一般取為－0.02；

k

為波數，其表達式為

k

＝2π/

λ

，

λ

為波長；

f

為運動頻率；

x

≥0.3

C

。根據以往的經驗，為獲得最佳的推進效果，

a

與

a

的關系為

a

＝－2

a

。圖2為網格劃分示意，考慮到翼型一直都在作橫向波動，除了翼型周圍采用非結構化網格，計算域其他地方均采用結構化網格。翼型表面第一層網格的高度滿足

y

≤1，使得第一層網格位于黏性底層區。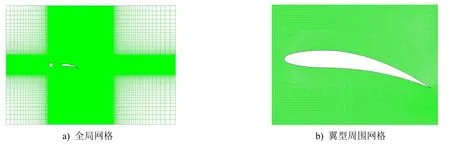

圖2 網格劃分示意

2 數值方法及驗證

2.1 控制方程

考慮不可壓縮流動湍流問題，其運動控制方程為

式(3)和式(4)中：

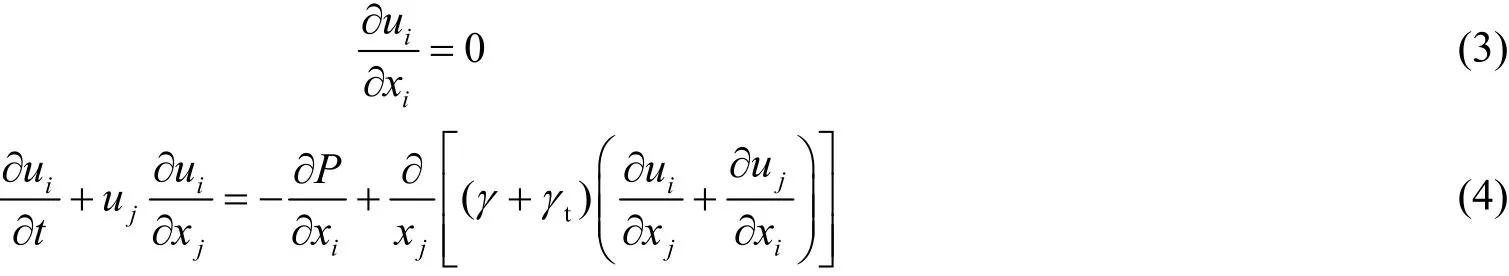
u

(

i

＝ 1,2)為流體運動速度；

x

(

i

＝ 1,2)為空間坐標；

P

為流體壓強；

γ

為運動黏性系數；

γ

＝

ck

ε

為湍流黏性系數，其中，

k

為湍流動能，

ε

為湍動能耗散率，

c

為常數。

2.2 動網格技術及精度驗證

在魚形體波動推進過程中，翼型邊界始終處于運動狀態，屬于典型的動邊界問題。對于動邊界問題的處理，采用商用軟件Fluent中的動網格技術可有效捕捉運動的邊界，通過用戶自定義函數（User Defined Function, UDF）控制邊界運動即可實現預定的運動。因此，本文采用Fluent中的動網格技術進行數值求解。

Fluent動網格技術中主要有3種調節計算內部網格節點的算法，分別為彈性光順、局部重構和鋪層。在彈性光順模型中，網格的邊被理想為網格節點間相互連接的彈簧，通過胡克定律計算網格邊界運動對整個彈簧系統受力的影響，進而通過調整各網格節點的位置，使之達到新的平衡狀態。該方法的網格變形較小，計算效率較高，尤其適于求解低頻率的變形運動問題。因此，本文選擇彈性光順模型處理運動邊界問題。

為驗證本文計算方法的可行性，對一個作行波推進運動的水翼進行數值模擬，計算模型采用與參考文獻[16]相同的模型，即弦長

c

＝0.1m的二維NACA0012水翼，來流速度設為

v

＝ 1.2m/s ，其他運動參數設置：

a

＝ 0.02；

a

＝－0 .08；

a

＝ 0.16；

λ

＝1.3；

f

的變化范圍為0.6～2.1Hz。計算擺動水翼在不同運動頻率下的推力系數

C

和推進效率

η

，計算結果見圖3，具體表達式為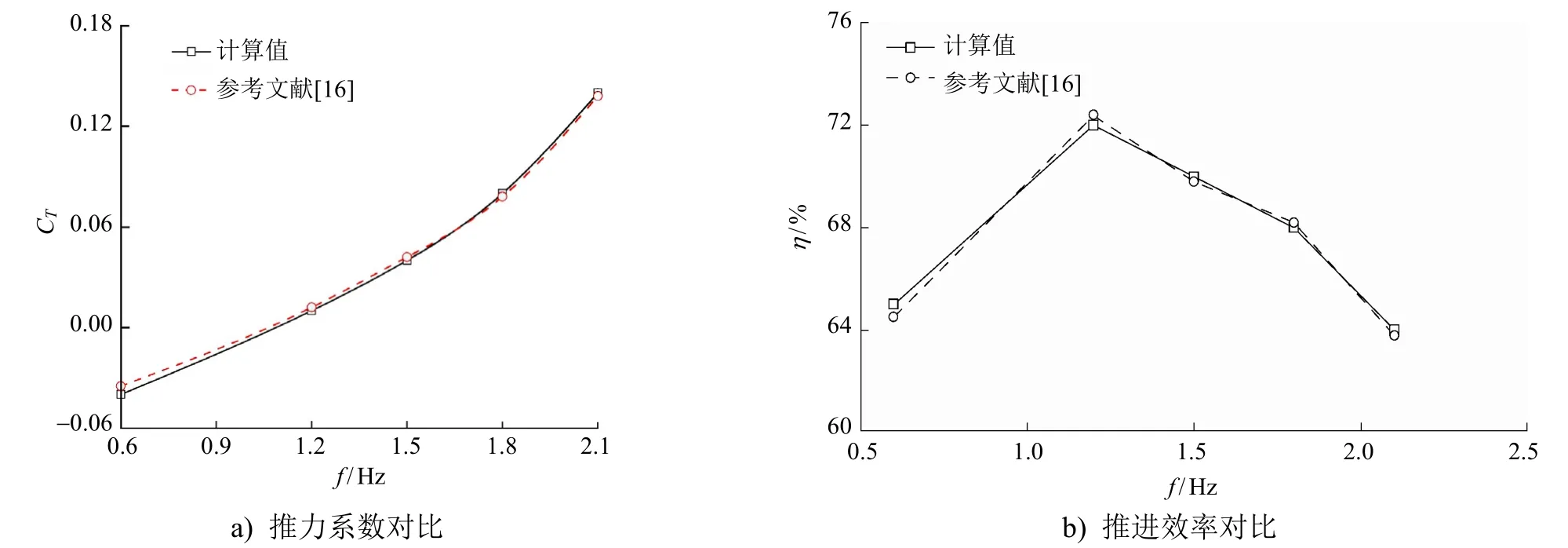

圖3 數值方法驗證結果

式(5)中：

T

為變形翼受到的推力；

P

為系統輸出功率；

P

為系統輸入功率，其含義為魚形體橫向振動時克服流體阻力所做的功；

p

和

v

＇分別為變形翼表面壓力和速度分布；

Γ

為變形翼邊界；

t

為某一運動時刻；

ρ

為流體密度；

C

為水翼的弦長；

l

為水翼的周長。

由圖3可知，本文的計算結果與參考文獻[16]中的計算結果能較好地吻合，因此本文建立的數值計算方法可用來研究擺動可變形翼的仿生推進性能。

3 計算結果和討論

3.1 渦流場與均勻流場中波動魚形體推進特性比較

首先對渦流場中波動魚形體與均勻流場中波動魚形體的推進特性進行比較。計算工況見表1，其中：SF1～SF4為均勻流場工況；UF1～UF4為渦流場工況。不同工況組合下魚形體推力系數和系統輸入功率隨運動頻率的變化曲線見圖4。

表1 計算工況

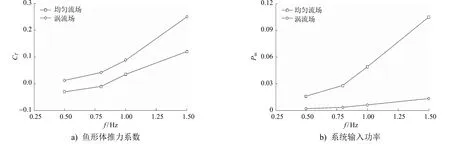
圖4 不同工況下魚形體推力系數和系統輸入功率隨運動頻率的變化曲線

1) 由圖4a可知，對于推力系數，在均勻流場中作波動推進的魚形體的推力系數小于在渦流場中作波動推進的魚形體的推力系數，尤其是在高運動頻率下，二者的差異更為顯著。此外，在低頻率運動工況下，均勻流中的波動魚形體獲得的推力為負值，這意味著魚形體無法產生向前的推力。相比之下，渦流場中的魚形體獲得的推力為正值，這意味著渦流場中的卡門渦街對魚形體的推進有積極作用。

2) 由圖4b可知，對于輸入功率，相同運動頻率下渦流場中的波動魚形體所需的系統輸入功率遠低于均勻流場中的波動魚形體所需的系統輸入功率，且運動頻率越高，二者的差距越明顯。特別是當運動頻率

f

=1.5Hz時，渦流場中魚形體的系統輸入功率僅為均勻流場中的1/8。這進一步說明，渦流場中存在的漩渦對魚形體推進有顯著的促進作用。圖5為SF和UF工況下魚形體周圍流線和壓力（

C

）云圖（

t

= 5

T

）。由圖5可知：流場上游方柱產生的漩渦流經過其后方的魚形體時，魚形體表面的流線發生改變甚至反轉，導致克服流體阻力消耗的能量減少；與均勻流場相比，渦流場中魚形體頭部的壓力相對較小，這正是渦流場中的魚形體能獲得較強推力的原因。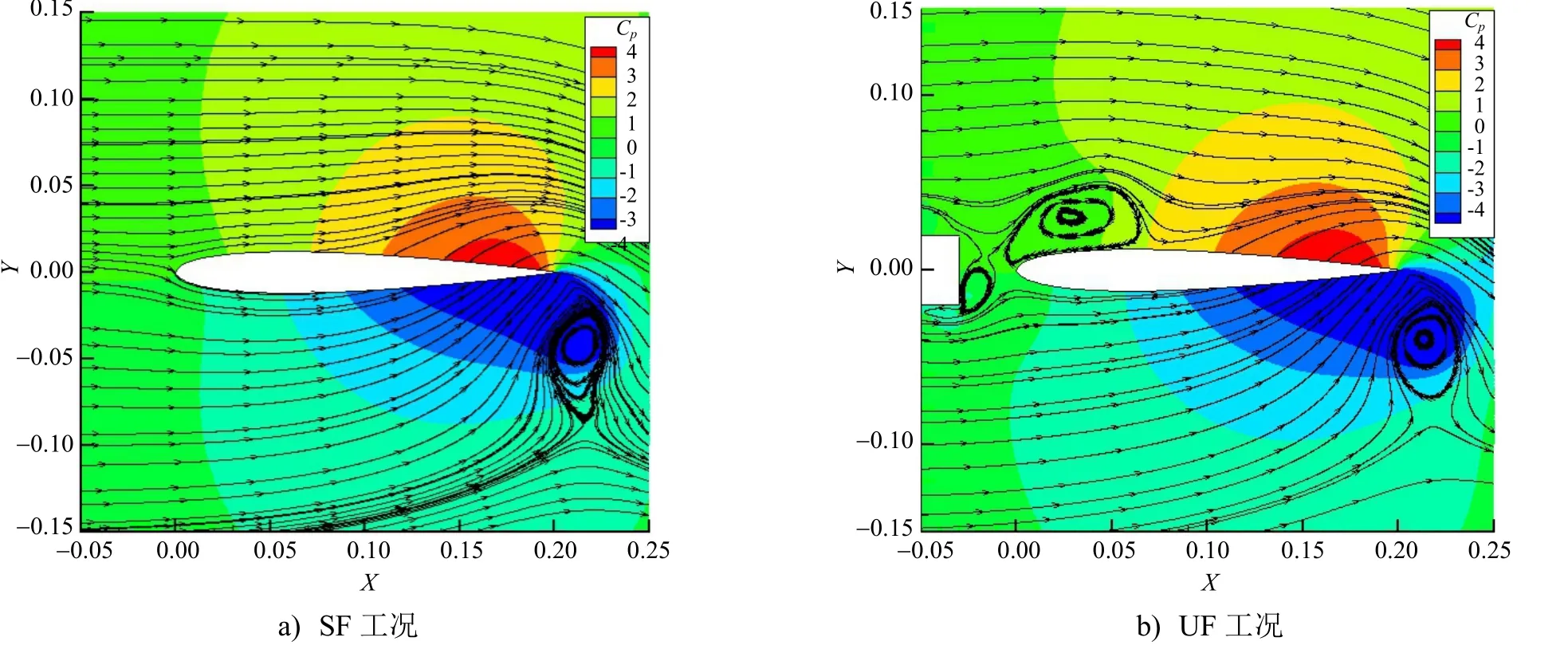

圖5 SF和UF工況下魚形體周圍流線和壓力云圖

3.2 方柱與魚形體的間距對魚形體推進特性的影響

系統分析方柱與魚形體的間距

S

對魚形體推進特性的影響。分別選取

S

的值為0.15、0.25、0.50、0.80和1.20，探究不同

S

下魚形體推力系數和推進效率的變化情況，計算結果見圖6。為更方便地對魚形體的推力系數進行分析，將推力系數分解為壓差造成的推力系數

C

和黏性導致的推力系數 v

TC

，即

式(6)中：

T

和

T

分別為壓差阻力和黏性阻力。為更直觀地顯示方柱與魚形體的相互作用，繪制不同

S

下魚形體后方的渦流場結構圖，結果見圖7，其中

Z

為流場

z

方向的渦量，其表達式為

式(7)中：

v

和

v

分別為魚形體在水平方向和垂直方向上的運動速度。

由圖6a和圖7可知，渦流場中波動魚形體受力可分為3種情況。

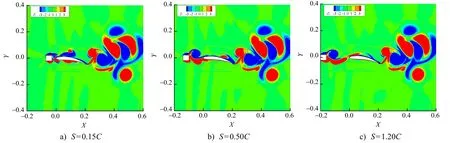
圖7 不同間距下魚形體后方渦流場結構

1) 當

S

＜0.5

C

時，由于魚形體與方柱之間的距離很短，魚形體的存在抑制了方柱的渦環脫落，且魚形體表面被方向相反的渦環覆蓋。魚形體的波動運動抑制了靜止方柱尾流場中剪切層的卷起和漩渦脫落，延伸了吸力區，使得其推力特性增強。此時，黏性阻力產生正的推力系數，且隨著

S

的增大，對應的

C

逐漸減小，使得整體的推力系數略有減小。2) 當0.5

C

≤

S

≤1.0

C

時，隨著魚形體與方柱之間的距離逐漸增大，方柱后方逐漸形成完整的上下交錯的渦環。魚形體的推力系數隨著

S

的增大而逐漸減小，且黏性阻力產生的推力 v

TC

也逐漸減小，直至為0。3) 當

S

＞1.0

C

時，魚形體與方柱之間的距離很大，方柱后方脫落的渦環在到達魚形體頭部過程中逐漸耗散，方柱與魚形體之間距離的影響明顯減弱。魚形體的推力系數迅速減小，黏性阻力產生的推力 v

TC

為負值。由圖6b可知，渦流場中魚形體的推進效率隨著

S

的增大呈逐漸減小的趨勢，尤其是當

S

＞0.5

C

之后，魚形體的推進效率更是大幅下降，這與推力系數的變化是一致的；當

S

繼續增大時，魚形體與方柱的相互作用逐漸減弱，推進效率值近乎不再發生變化。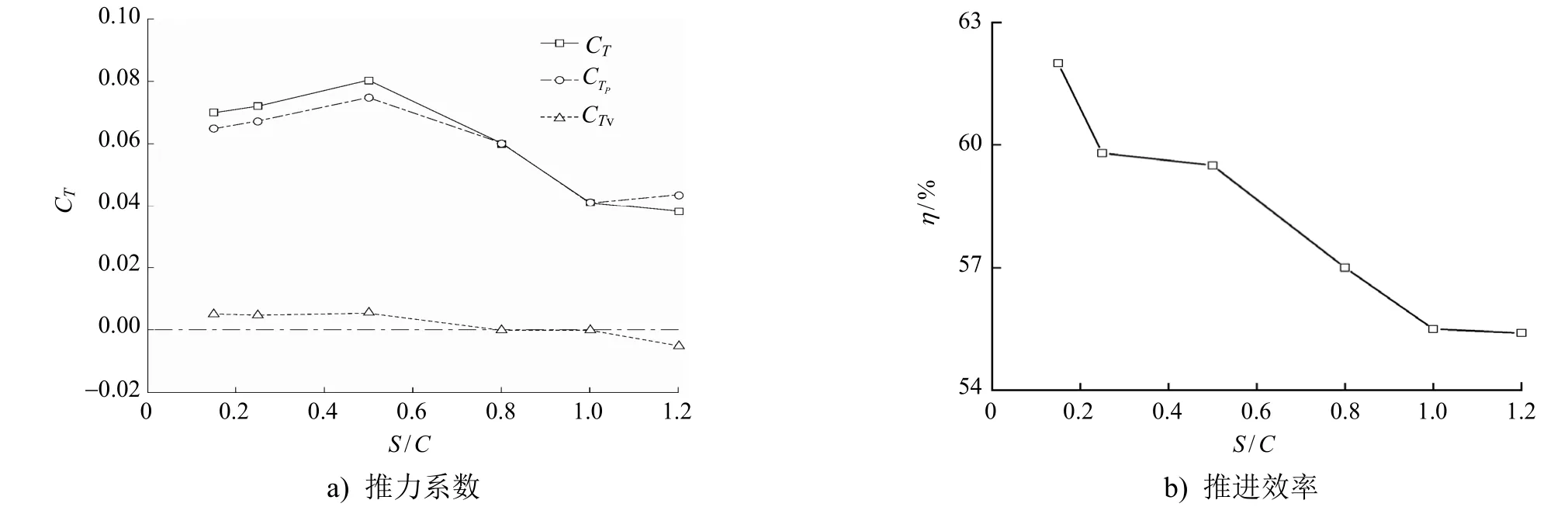

圖6 平均推進力系數和推進效率隨魚形體與方柱間距的變化曲線

4 結 語

本文通過在魚形體上游布置一個靜止方柱模擬渦流場環境，采用動網格技術對渦流場中波動魚形體的推進特性進行數值模擬研究，系統分析方柱與魚形體間距對魚形體推進特性的影響。數值計算結果表明：與均勻流場中的波動魚形體相比，渦流場中的波動魚形體可獲得更大的推力，且消耗的功率較少；渦流場中波動魚形體的受力情況隨著方柱與魚形體間距的變化而有所不同，隨著二者間距的增大，魚形體的推力呈逐漸減小的趨勢。