視覺測量方法

易懷安 趙欣佳 唐 樂 陳永倫

桂林理工大學機械與控制工程學院，桂林，541006

0 引言

表面粗糙度是工件加工過程中刀具在其表面留下來的刀痕產生的，它是衡量機械零件的一個主要幾何精度指標，對零件的配合性質、耐磨性、抗腐蝕性以及密封性等會產生顯著的影響。傳統的表面粗糙度測量方法是利用觸針式測量設備，其主要工作原理是用觸針裝置的探頭劃過工件表面，并監測探頭運動，測量工件表面的截面高度信息。該測量方法的檢測精度受探針半徑影響較大，且不支持在線測量，效率低下。此外，當被測工件的表面較軟時，其表面存在被探頭劃傷的風險。為解決上述問題，一些研究者已開發了許多非接觸的光學測量設備，如白光干涉儀、原子力顯微鏡和激光顯微系統等。但這類測量設備由于成本高、受工作環境影響較大和測量視野較窄等原因，在一定程度上限制了其工程應用。而機器視覺測量是基于光學成像原理的測量方法，利用工業相機采集工件的表面圖像，然后提取圖像中與表面粗糙度參數相關的特征指標，進而可預測已知圖像特征指標對應位置的表面粗糙度。該方法具備單次測量面積大、效率高、非接觸、可實現自動化測量、成本較低等優點，近二三十年來得到了國內外許多研究者的廣泛關注[1-3]。目前基于機器視覺測量表面粗糙度的評價指標大多是從灰度圖像中提取相關評價指標來表征粗糙度[4-7]，忽視了顏色信息具有信息量豐富、抗污染、測量精度高等優點。針對這一問題，近年來一些研究者開展了基于顏色信息指標對表面粗糙度進行機器視覺測量的研究。YI等[8-9]提出基于RGB顏色空間三基色之間的色差(color difference,CD)算法與彩色圖像清晰度算法，構建此類指標與表面粗糙度的關系模型。LU等[10]構造一種顏色分布統計矩陣來表征兩種光源在粗糙度表面形成的混疊虛擬圖像，并根據顏色分布統計矩陣設計純色能量指標和混疊區域面積指標來建立與表面粗糙度的關系模型。LIU等[11]依據光源在不同粗糙度表面形成虛像的擴散區域不同，設計基于紅綠顏色空間的紅綠重疊指數來評價表面粗糙度。雖然這些研究相對灰度圖像都取得了不錯的實驗結果，但彩色圖像每個像素點都是由紅、綠和藍三個分量按比例混合而成，它們存在一定的制約關系。如果只對圖像的某個通道單獨處理，則會破壞顏色信息的整體性，而上述顏色信息評價指標均建立在紅、綠兩種顏色的分布差異上。此外，這些表征粗糙度的顏色信息指標沒有基于數學意義上的合理數據結構表達。

針對上述問題，本文提出利用四元數對彩色圖像進行建模，充分考慮彩色圖像作為一個整體所具有的顏色信息，利用純四元數的三個虛部來分別代替彩色圖像中紅、綠和藍三個顏色通道，基于不同粗糙度表面對光的反射成像所攜帶輻射能量分布的差異，對四元數進行奇異值分解，進而構造奇異值熵指標來評價磨削表面粗糙度。

1 圖像奇異值熵評價方法機理

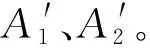
I(x，y)=f(L(x，y)，F(x，y)，R(x，y))

(1)

其中，照度L(x，y)表示照射在磨削表面上的光照強度，是單位面積上所接受可見光的能量；表面特性F(x，y)包括表面粗糙度和表面紋理方向；反射R(x，y)表示粗糙表面將光線反射到相機里的能力。對于灰度圖像，圖像質量I(x，y)以灰度值表示；對于彩色圖像，圖像質量I(x，y)在RGB顏色空間以紅、綠和藍三個分量值表示。因此，當照度L(x，y)和材料表面反射R(x，y)一定時，表面特性F(x，y)則與圖像質量I(x，y)密切相關。而本文的實驗正是在同一種光照和材料的條件下進行的。事實上，表面特性F(x，y)在微觀上反映了材料表面高低變化程度(即材料表面粗糙度)，故理論上可認為RGB顏色空間的圖像質量I(x，y)與表面特性F(x，y)存在一定的內在聯系。

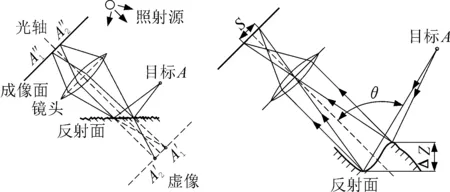
(a) 粗糙表面對成像 的影響 (b) 粗糙高度方向對成像 的影響圖1 粗糙表面成像示意圖Fig.1 Diagram of rough surface imaging

由能量守恒定律可知，假設一束光以一定角度照射到物體表面時，若忽略金屬表面所吸收的光能量，則大部分光會被反射，但由于物體表面非理想光滑，所以一部分光會發生漫反射到空間各個方向，而反射光的能量也將被削弱。由此可知，反射光與散射光能量的強弱分布是由物體表面粗糙度決定的[16]，而這一特征則會在相機捕獲的圖像中表現出來。

根據幾何光學的反射成像定律，反射光在不同的粗糙度表面發生漫反射的擴散程度必定不同。表面粗糙度越小，表面擴散程度越低，反射光線集中性越強，這時表面成像越清晰，故當表面成像越清晰時，圖像能量分布情況比較集中，反之能量分布越分散。而奇異值大小的分布與圖像的能量相映射[17]，則奇異值矩陣能表征圖像能量分布的情況。此外，根據香農信息論理論，熵越大，所含的信息量越多，圖像質量評價中也認為熵越大，圖像就越清晰，故將熵引入奇異值矩陣中，通過構造奇異值熵指標來評價磨削表面粗糙度。當奇異值熵越大時，圖像越清晰，能量分布越集中，反之越分散。

2 奇異值熵算法

四元數(Quaternions)也稱為超復數[18]，它由四個部分組成，包含一個實部和三個虛部，表達式如下：

q=a+bi+cj+dk

(2)

式中，b、c、d為實數；i、j、k為四元數的3個虛數單位；a為四元數的實部，若a=0，則稱式(2)為純四元數。

PEI等[19]發現了四元數的數據結構與彩色圖像RGB顏色矢量具有良好的對應關系，使得該技術在彩色圖像處理領域得到了廣泛關注。這種方法為顏色信息矢量在數學意義上提供了較為合理的數據結構表達，對于一幅彩色圖像上任一點(x，y)，有

Q(x，y)=R(x，y)i+G(x，y)j+B(x，y)k

(3)

式中，Q(x，y)為彩色圖像的純四元數矩陣；R(x，y)、G(x，y)、B(x，y)分別為基于矩陣形式的紅色、綠色和藍色分量。

根據式(3)可建立彩色圖像的四元數矩陣A，本文參考文獻[20]給出了四元數矩陣的奇異值分解定義，其表達式如下：

(4)

Sr=diag(δ1，δ2，…，δr)

式中，Sr為圖像奇異值矩陣；δi(i=1，2，…，r)為Sr的非零奇異值，r為奇異值總數，且滿足δ1≥δ2≥…≥δr；U、V*為四元數酉矩陣。

根據式(4)可對一幅彩色圖像的四元數矩陣進行奇異值分解，從而得到彩色圖像的奇異值矩陣，進而可構造出奇異值熵，計算方法如下。

對得到的圖像奇異值矩陣Sr=diag(δ1，δ2，…，δr)進行歸一化處理：

(5)

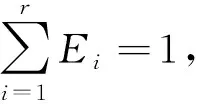
根據信息熵的定義，對四元數進行奇異值分解，進而構造奇異值熵指標(即QSE指標)，其計算表達式如下：

(6)

結合奇異值衰減迅速的特性[21]和較小奇異值可視為噪聲，本文選取奇異值數量為r=20。

3 實驗方案設計

為更好地說明本文所提QSE指標具備一定的優勢和可行性，本文選取了色差(CD)指標[9]與所提QSE指標進行了對比分析驗證，且本實驗設計方案與CD指標的實驗設計方案類似。圖2a為實驗方案模型圖，其中磨削樣塊檢測面垂直于工作臺水平面，樣塊紋理方向與工作臺水平面平行，色塊(圖2b)與工作臺水平面成45°夾角。相機光軸與色塊平行，便于相機能更好地捕捉到色塊在磨削試樣表面所形成的虛像。由于LED光源具有穩定性較好、均勻照明、亮度可控等優點，因此本實驗采用LED白色條形光源作為照射源。圖2中的主要設備包括500萬像素分辨率的彩色CCD相機、連接CCD相機的計算機、LED光源控制器和光學精密平臺。色塊的材質為紙，尺寸為150 mm×150 mm。圖3所示為實驗的具體流程。

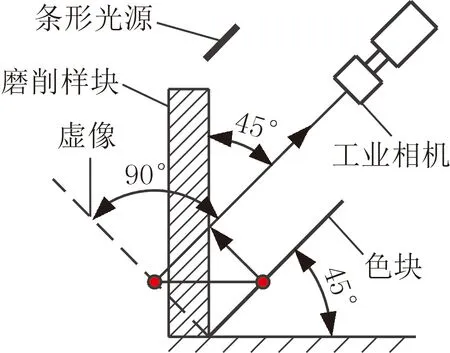
(a) 實驗模型 (b) 色塊

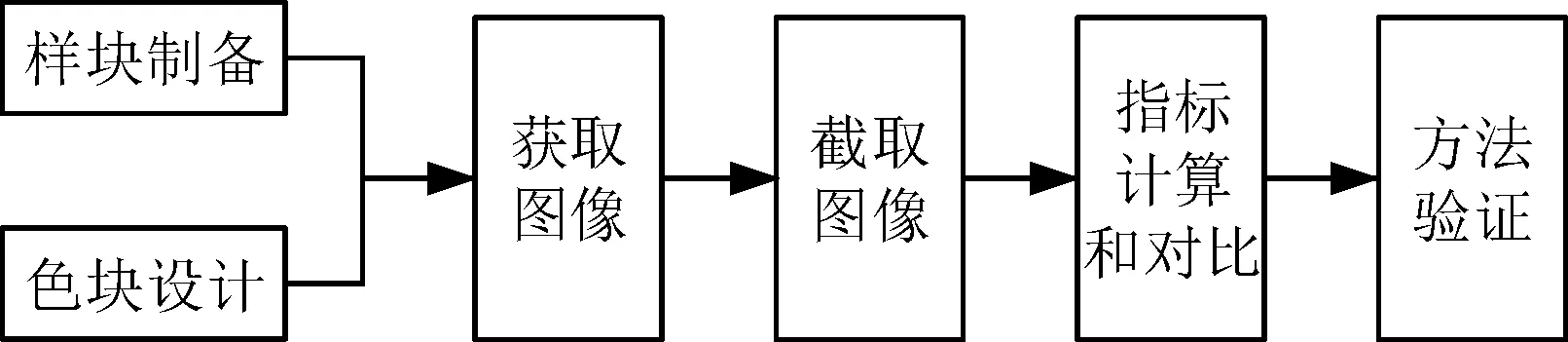
圖3 實驗具體流程圖Fig.3 Experimental specific flowchart

4 實驗結果與數據分析

4.1 實驗結果

表1所示為在手動磨床上加工的20個樣塊采用觸針式測量儀得出的測量結果。表1中所有試樣的實驗條件一致，所截取的圖像尺寸為1200 pixel×1200 pixel，并盡可能保證所截取的圖像中紅綠顏色區域對稱。同時，選取表1中偶數序列號的樣本作為標定樣本，這樣使樣本分布較為均勻且粗糙度等級范圍較廣，其余10個作為驗證樣本使用。作為對比的CD指標的計算公式如下：

(7)

式中，R(x，y)為圖像紅色分量對應坐標點的灰度值；G(x，y)為圖像綠色分量對應坐標點灰度值。

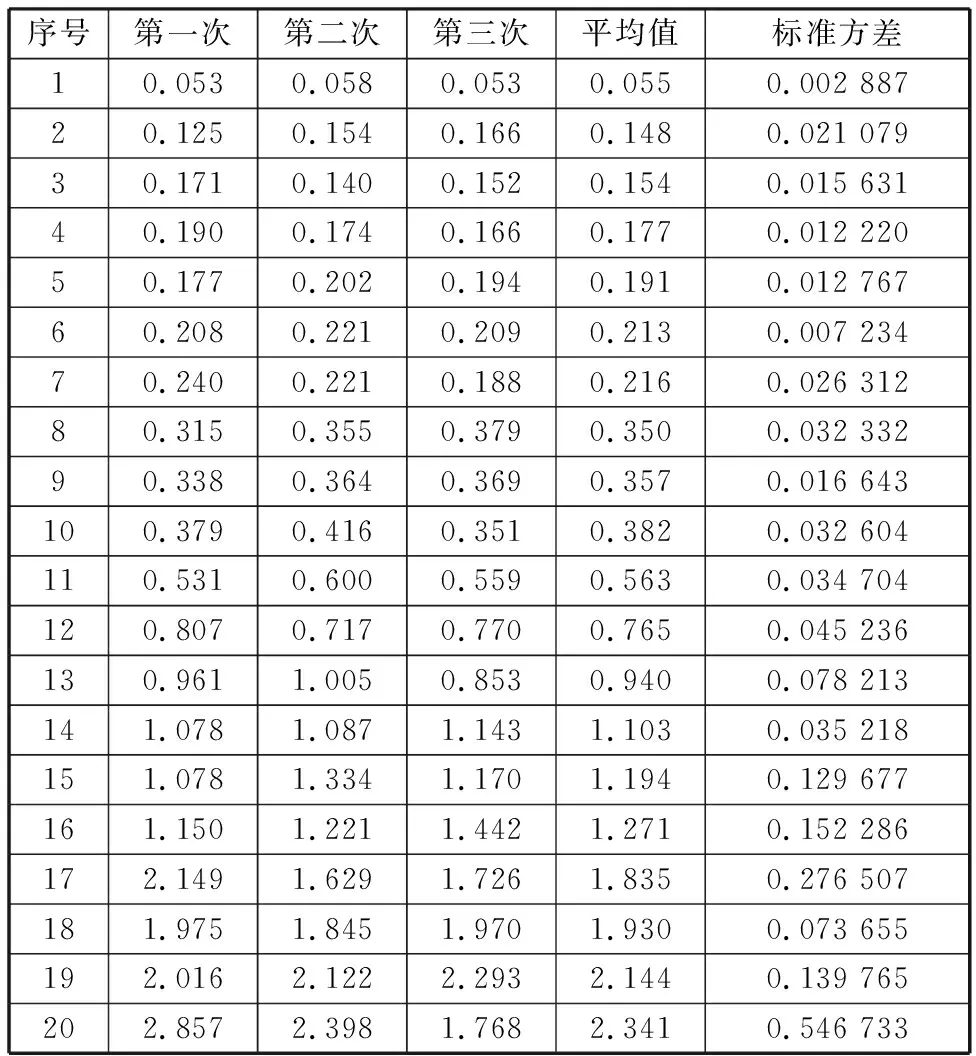
表1 觸針式測量試樣表面粗糙度

為了驗證所提QSE指標具備一定的預測能力，本文利用支持向量機(SVM)對樣本數據進行回歸擬合，以達到預測表面粗糙度的目的，各指標擬合結果如圖4所示。表2、表3所示分別為各指標的計算結果和預測結果。為了便于指標的對比，本文對兩種指標值做了歸一化處理，兩種指標歸一化之后的對比情況如圖5所示。此外，為了說明所提指標與表面粗糙度值具有較好的相關性，本文利用皮爾遜相關系數(表4)來對指標進行驗證，其計算公式如下：

(8)

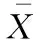
(a) CD指標

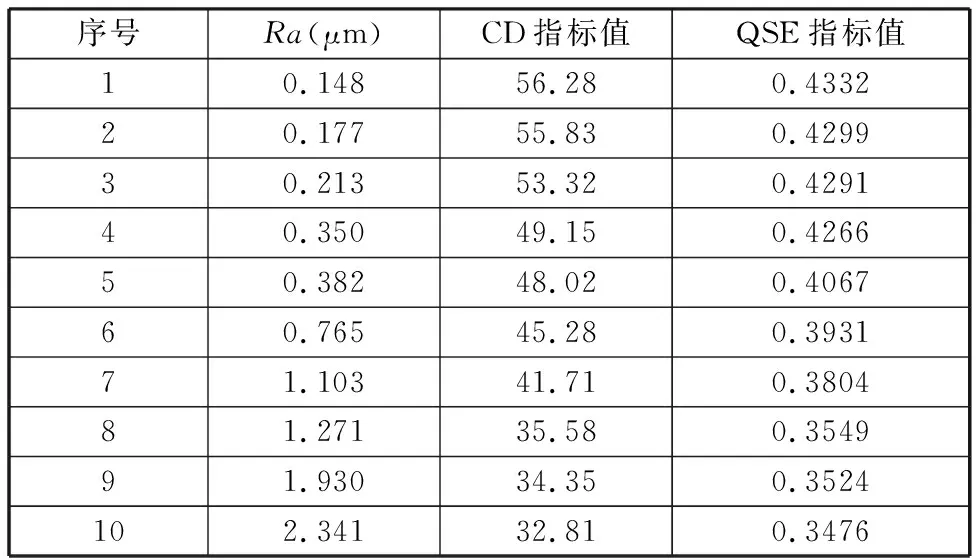
表2 不同指標的計算結果

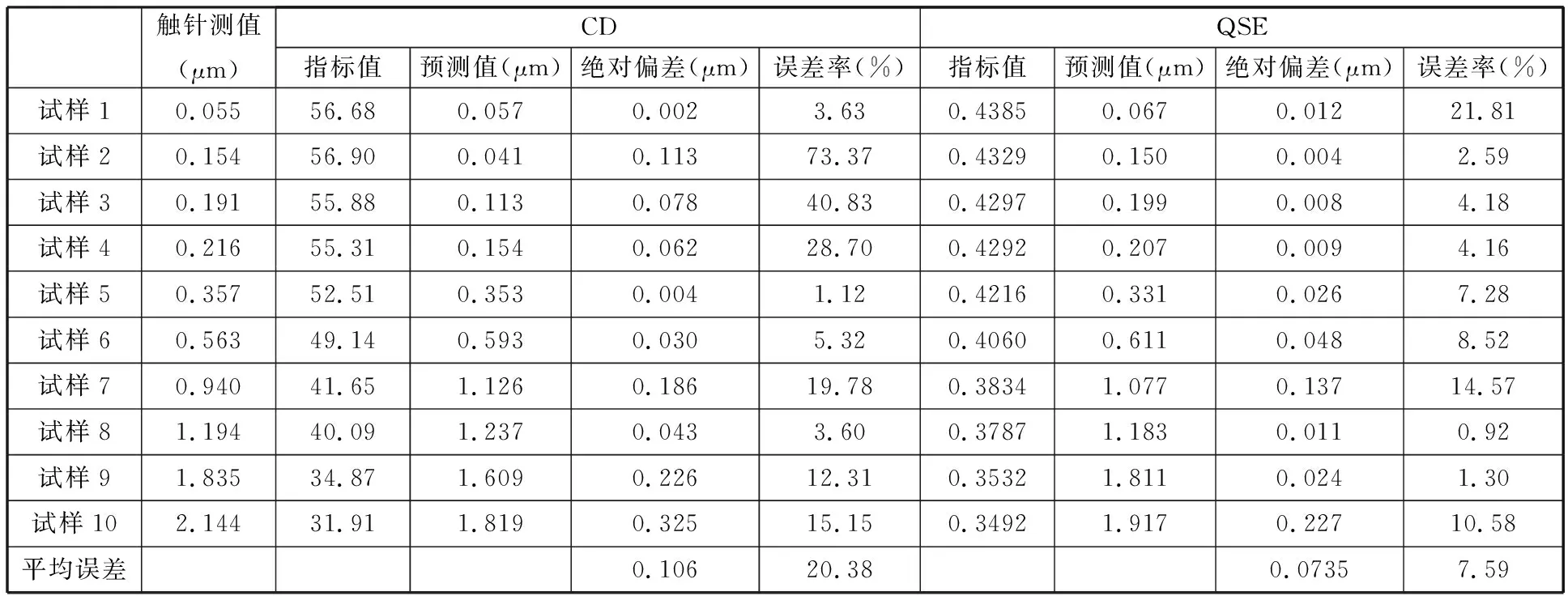
表3 驗證樣本預測結果

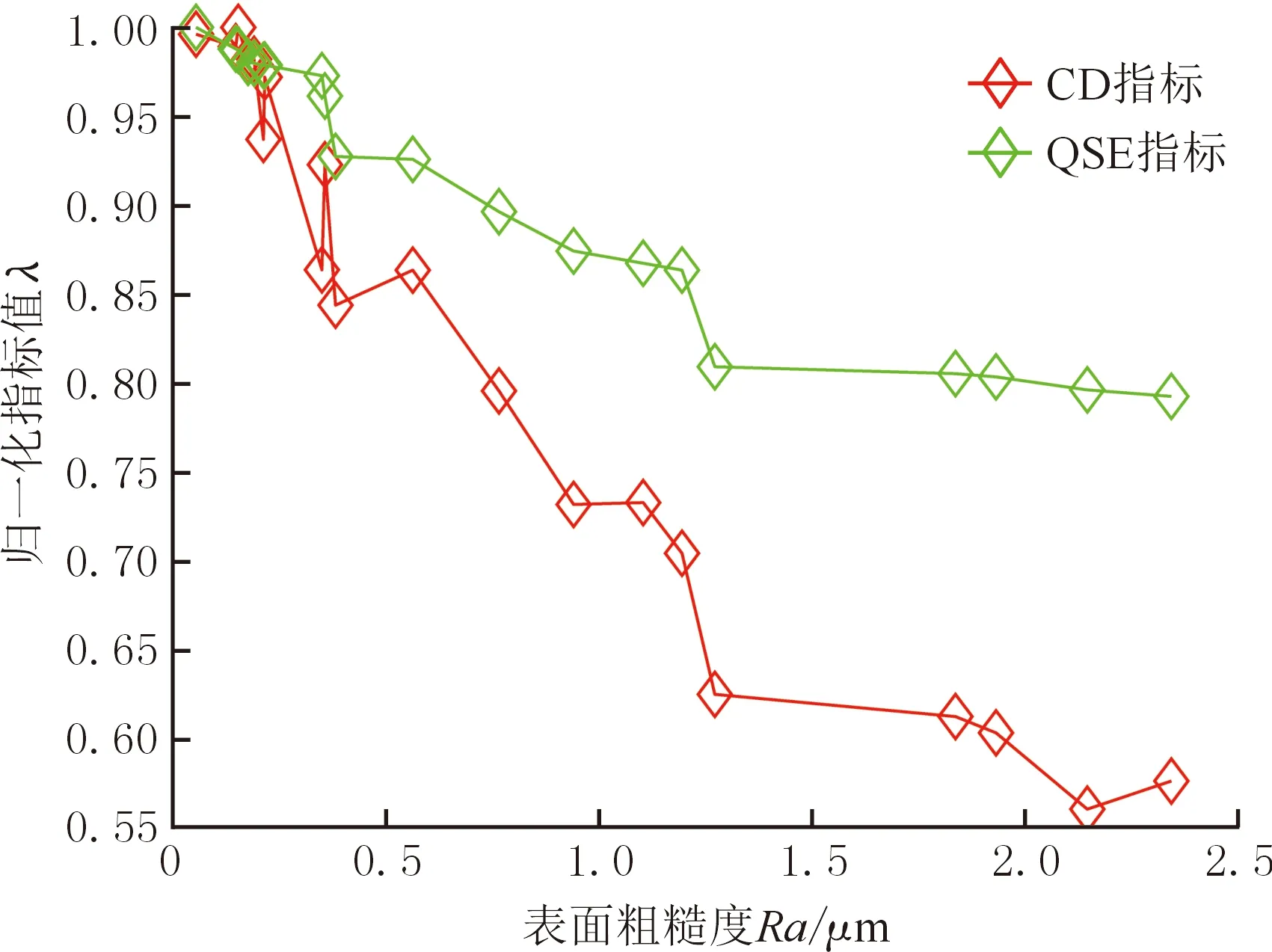
圖5 CD和QSE指標總體趨勢對比Fig.5 Comparison of overall trends of CD and QSE indices

表4 不同指標相關系數R值

4.2 數據分析

從表1中可以看出，利用觸針式測量設備所測得的三次測量值大多都在其平均值附近波動，且偏差程度較低，這說明每次觸針測得的表面粗糙度值較為準確。為了提高測量精度，將三次測量的平均值作為磨削樣塊的表面粗糙度值。但隨著樣塊表面粗糙度的增大，其測量得到的標準方差值有逐漸增大的趨勢，產生這種現象的原因是觸針式測量儀是對試樣表面進行線性采樣測量，其測量精確度受每次線性取樣的長度和取樣面積影響。

由表2和表3可以看出，無論是CD指標值還是QSE指標值都隨著表面粗糙度值的增大呈現單調遞減的趨勢，說明本文所提指標具有一定的可行性。在預測能力方面，CD指標的預測值與實際測量值的絕對偏差明顯大于QSE指標對應的絕對偏差；CD指標的平均誤差率達到了20%，而QSE指標平均誤差率僅為7%，因此QSE指標具備更高的預測精度。兩種指標在平均誤差率方面相差較大的主要原因是CD指標的單調性較弱，其指標值的波動性較大，這從圖5所示的指標趨勢對比圖中就可以看出，而QSE指標的檢測穩定性較好。此外，圖5所示的CD指標比QSE指標表現出了更強的遞減性，產生這種現象的主要原因與兩個指標的取值范圍有關，當對整個圖像取CD指標值時，其平均值受分界線附近每個像素點的影響較大，如圖6所示，隨著表面粗糙度值的增大，CD指標紅綠分界線處的溝壑狀雖有所減緩，但依舊非常明顯。而QSE指標是基于圖像的能量信息，其能量值受整幅圖像所有像素點變化的影響，如圖7所示，隨著表面粗糙度值的增大，QSE指標的能量三維圖變化并不明顯，與QSE指標相比，CD指標變化的劇烈程度更高。

(a) Ra=0.055 μm (b) Ra=0.531 μm (c) Ra=2.341 μm圖6 CD指標灰度三維圖Fig.6 CD index grayscale 3D image

(a) Ra=0.055 μm (b) Ra=0.531 μm (c) Ra=2.341 μm圖7 QSE指標能量三維圖Fig.7 QSE index energy 3D image

由圖4所示的各指標與表面粗糙度擬合情況可以看出，QSE指標與表面粗糙度值的擬合情況優于CD指標，說明QSE指標與表面粗糙度具有較好的魯棒性，表4所示的相關系數也間接證明了本文所提指標與表面粗糙度的相關性要優于CD指標。如果僅比較兩種指標的相關系數R的大小，則CD指標的R值絕對值比QSE指標的R值絕對值僅小0.033，但CD指標依賴于特定的光源，而QSE指標在無需色塊反射的情況下就可完成對試樣表面粗糙度的檢測，其適用性必定強于CD指標。

此外，本文提出的奇異值熵QSE指標較已有研究中提出的清晰度[8]和CD[9]指標的數學解釋更為科學，可構建數學意義上的理論模型，可為日后實現表面粗糙度機器視覺自動化檢測提供一定的理論依據。

5 結論

(1)本文提出了一種基于彩色圖像奇異值熵指標(QSE指標)評價磨削表面粗糙度的方法，通過與色差(CD)指標進行對比實驗分析，發現QSE指標與表面粗糙度的相關性較好，且采用支持向量機擬合回歸預測的結果也較為精準，表明所提指標具備一定的可行性和優勢。

(2)所提指標相對評價表面粗糙度所常用的灰度圖像特征指標而言，解決了圖像格式轉換過程中顏色信息丟失問題；對比已有的一些基于彩色圖像信息的評價指標，該指標將圖像顏色信息作為一個整體處理，并給出了圖像顏色信息在數學意義上具有合理解釋的矢量數據結構表達方式及計算方法。