HTI介質地震波各向異性AVO反演

李 勤，王 瑋，王瀚林

(西安科技大學 地質與環境學院，陜西 西安 710054)

HTI(Transverse Isotropy with a Horizontal axis of symmetry)介質是一種具有近似水平對稱軸的橫向各向同性介質，對于含有垂直裂隙的模型，可將其近似等效為HTI介質模型[1]。HTI介質是一種典型的各向異性模型，THOMSEN[2]提出通過各向異性參數來描述介質的各向異性程度，并推導了各向異性參數與彈性參數之間的量化關系;董守華[3]針對煤層進行了各向異性參數測試，討論煤層各向異性參數與孔隙率的關聯，并指出通過煤層各向異性的大小和方向能夠預測煤層的裂隙密度和方位;陳同俊等[4]利用介質等效模型理論分析了構造煤的各向異性AVO(Amplitude Variation with Offset)特征，對不同的AVO近似方程應用于煤層的效果進行比較，對AVO近似方程進行改進，使其能適用于各向異性煤層。彭蘇萍和畢銀麗[5]指出煤層在開采過程中會產生裂隙。許多專家研究了各向異性參數與裂隙之間的關聯，SCHOENBERG和DOUMA[6]針對含平行裂隙的介質，將其等效為無限薄無限柔順的薄層，忽略裂隙的形狀及其空間分布細節，假設裂隙面處位移張量不連續，但牽引力張量連續，且2者線性相關，提出了線性滑動理論，建立了裂隙介質等效模型;BAKULIN等[7]提出用裂隙弱度來描述裂隙，分析裂隙流體因子與裂隙充填物的關聯;QUINTAL[8]研究了飽和流體研究中流體飽和度對反射系數的影響;陳懷震等[9]通過分析流體因子對不同流體的響應關系，指出HTI介質中裂隙飽和水時，裂隙流體因子值偏小，趨近于0;郎玉泉等[10]利用Gassmann方程進行流體替代，通過AVO正演，估計頂板砂巖孔隙度和干濕性。AVO反演的基礎是反射系數近似式，RüGER[11]首先給出不同的橫向各向同性介質的縱波反射系數近似公式，近似式精度較高，是目前AVO理論的基礎[12-13]。利用反射系數近似公式，可以實現地震疊前AVO反演[14-16]。MA[17]利用模擬退火法，通過疊前AVO反演得到了巖石特性;MISRA和SACCHI[18]利用快速模擬退火法解決了基于邊界保護的AVO反演問題，粒子群算法最早由Eberhart提出，源于對鳥群捕食行為的擬態[19]，MIKKI[20]將這種方法用于電磁優化，使該算法進入工程物探領域并得到發展，SUN等[21]基于粒子群算法進行儲層預測，收到一定成效;SUN和LIU[22]利用混沌量子粒子群算法求解了疊前AVO彈性參數;MEHRGINI等[23]利用粒子群算法對具有中子孔隙度、體積密度、水飽和度時的地層橫波速度VS進行了反演并論證;WU等[24]利用粒子群算法對地層的縱橫波速度、密度進行了反演;嚴哲等[25]利用量子粒子群算法對Marmousi2模型的縱橫波速度和密度進行了反演，反演結果穩定。對反演算法進行改進和優化是提高反演精度和反演效率的主要手段，對于疊前AVO反演來說，粒子群算法(PSO,Particle Swarm Optimization)雖然收斂速度快、原理簡單，但卻容易早熟，陷入局部最優;模擬退火法(SA,Simulated Annealing)雖然全局尋優能力強但其穩定性又不能得到保證。因此，在粒子群算法的基礎上結合模擬退火的思想，對粒子群算法進行改進，使新算法有強行跳出局部最優解的能力，這種優化后的混合算法在反演時具有明顯的優越性和有效性。筆者基于HTI介質反射系數近似公式，建立關于各向異性參數的目標函數，采用基于模擬退火的優化粒子群算法(SA-PSO)實現HTI介質疊前AVO反演，并通過裂隙流體因子與各向異性參數的關聯，實現流體因子預測。

1 HTI介質各向異性AVO反演理論及步驟

1.1 基于模擬退火的優化粒子群算法反演原理

粒子群算法是通過模擬鳥類覓食的過程，達到解決優化問題的方法，算法收斂速度快。在粒子群算法中，鳥類被抽象為沒有質量和體積的微粒，并延伸到n維空間，粒子i在n維空間的位置表示為向量Xi=(x1,x2,x3,…,xn)，飛行速度表示為向量Vi=(v1,v2,v3,…,vn)，粒子不僅知道自己發現的最好位置Pb，也知道整個群體中的其他粒子發現的最優位置Pb,g，粒子們根據這些信息來決定接下來的行動方向。根據目標函數的構建，每個粒子都有其適應值范圍。粒子群優化算法首先將粒子初始化為一群隨機粒子，然后通過迭代找到最優解，在每一次迭代中，粒子通過跟蹤兩個“最優解”(即Pb,Pb,g)來更新自己，在找到“最優解”(Pb,Pb,g)后，粒子通過下式更新自己的位置:

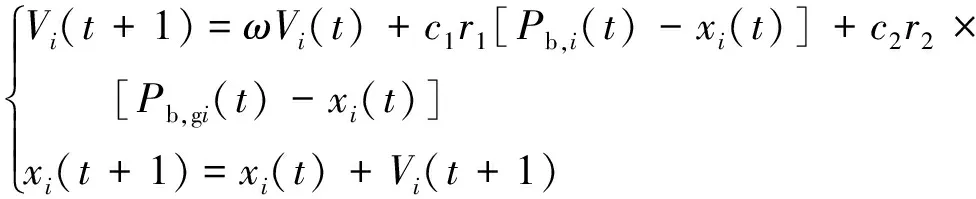
(1)

式中，Vi(t)為粒子i在t時刻的速度;ω為慣性因子;c1和c2為學習因子，分別為粒子的局部學習能力和全局學習能力;r1和r2為[0，1]的隨機數;Pb,i(t),Pb,gi(t)分別為粒子i和群體中其他粒子在t時刻為止發現的最好位置;xi(t)為粒子i在t時刻的位置。

在搜索過程中，粒子的尋優范圍局限在Pb附近，因此不能保證全局收斂得到全局最優解，而慣性因子ω表示的就是繼承先前粒子速度的能力，當ω較大時，繼承粒子前一時刻速度較多，全局尋優能力會有所提高。ω的值如果過大或過小就會造成算法陷入局部尋優或者無法找出最優解。因此，對慣性因子進行實時調整很有必要。針對ω在算法運行各個階段的不同作用，加入隨迭代次數非線性減小的慣性因子。減小的慣性因子公式為

ω(k)=ωs-(ωs-ωe)(k/Tmax)2

(2)

式中，ωs為初始慣性因子;ωe為迭代至最大次數時的慣性因子;k為當前迭代次;Tmax為最大迭代次數。

學習因子c1和c2影響算法的全局和局部搜索能力，c1為粒子的個體認知，因此影響局部搜索能力;c2為群體認知，影響全局搜索能力。在粒子群優化算法迭代過程中，迭代前期需要粒子群優化算法的全局搜索能力強，隨著迭代進行至后期，算法需要快速收斂，此時需要局部搜索能力強。因此，在粒子群優化算法加入自適應的學習因子使得算法找到更優解乃至最優解。學習因子自適應公式為

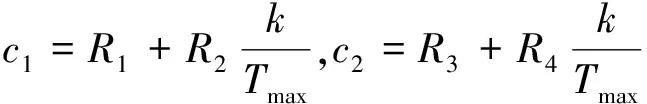
(3)

式中，R1,R2,R3,R4為學習因子的自適應度參數。

在粒子群算法中，粒子在發現的當前最優位置靠近局部最優解的時候，所有的粒子就會聚集到最小的區域，全局搜索能力就會削弱。而模擬退火法的優勢正在于通過調整溫度，控制概率性跳出特性，進行新一次的隨機搜索，將模擬退火的這種特性引入到粒子群算法，可以有效避免陷入局部最優解，這種修正主要是針對全局最優位置Pb,g，利用模擬退火的跳出機制來選擇每個粒子的當前最優位置，即通過控制模擬退火法對“變差解”的接受概率，可以提高粒子群算法的靈活性，增加粒子的多樣性。模擬退火法通過在求解區間隨機游走，利用Metropolis抽樣準則使隨機搜索最新位置逐漸收斂于最優解。Metropolis準則定義了某一溫度下系統狀態從狀態i到狀態j的能量概率為

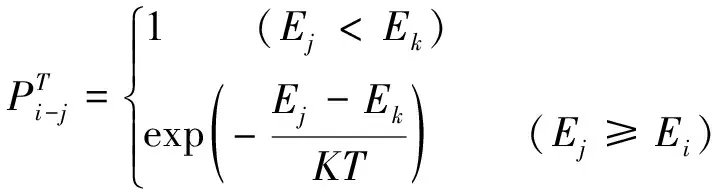
(4)

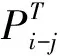
在模擬退火的跳出機制下，認為Pb是和Pb,g懸殊很大的特殊解，可以計算出溫度為T時Pb相對Pb,g的能量概率，即exp(-fPb-fPb,g)T，其中f為目標函數解值。若將所求概率作為Pb的適配值，則用Pb替代Pb,g。

1.2 HTI介質反射系數與裂隙流體因子

HTI介質通常是由平行排列的垂直裂隙形成，即對稱軸接近于水平方向時的TI介質。HTI介質彈性矩陣:

(5)

由于HTI介質在垂直面彈性參數相同，根據矩陣對稱性，其彈性參數有如下關系:

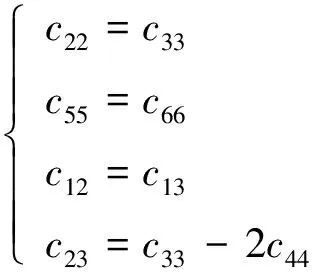
(6)

根據Thomson各向異性介質理論，HTI介質的各向異性參數和彈性參數可由式(7)進行計算

(7)

其中，VP為縱波速度;ρ為密度;VS為橫波速度;ε(v),δ(v),γ(v)為HTI介質的Thomsen各向異性參數，ε(v)為縱波各向異性程度，δ(v)為縱波在橫向和垂向之間各向異性變化的快慢程度，γ(v)為快、慢橫波速度的差異程度。

基于Thomsen各向異性參數，RüGER給出了HTI介質的PP波反射系數公式:

(8)

根據線性滑動模型理論中應力與裂隙應變的關系，裂隙介質彈性系數矩陣C可以表示成各向同性背景系數矩陣Ciso加上各向異性擾動Cani之和，則描述TI介質的裂隙等效彈性矩陣為

C=Ciso+Cani

(9)

其中，令λ+2μ=L，則Ciso,Cani分別為

(10)

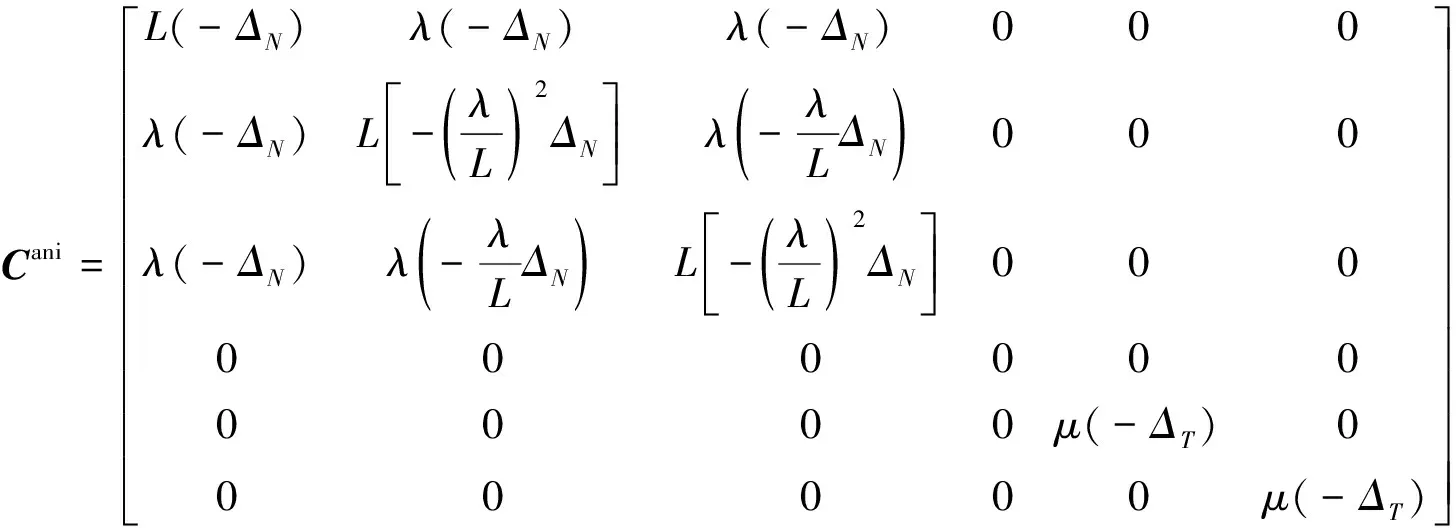
(11)

設g=μ/(λ+2μ)=(VS/VP)2為各向同性巖石骨架橫波速度和縱波速度比值的平方，經推導得到裂隙剛度矩陣中的ΔN和ΔT表達式:

(12)

式中，ΔN和ΔT為Schoenberg線性滑動理論中的裂隙法向弱度和切向弱度，其絕對值在0～1;e為裂隙密度;g為橫縱波速比的平方;Kf和μf為裂隙充填流體體積模量和剪切模量;λ和μ為不含裂隙巖石的拉梅系數;a/c為裂隙縱橫比，a,c分別為裂隙縱向長度，橫向寬度。

結合Thomsen各向異性參數和線性滑動模型等效理論，經推導可以得到HTI介質各向異性參數與裂隙柔度參數之間的表達式為

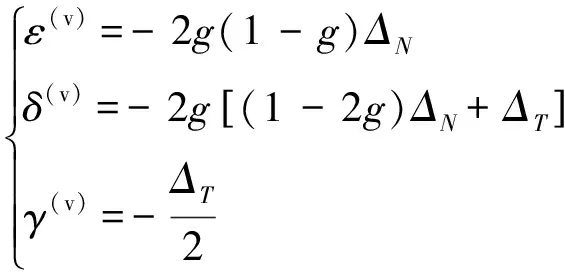
(13)

所以，ΔN和ΔT可由各向異性參數表示為

一直以來，產業界人士都在爭議自動化技術能否永久性、大規模取代人工勞動。按照經濟學中的“比較優勢”理論，即便技術進步，人類也仍然會在很多領域保持優勢。因此，技術不會取代人工勞動，而是釋放了工人，讓人類可以從事不具有危險性，但更具挑戰性的工作。但要承認，機器沒有人類的弱點和偏見，更加不偏不倚、不主觀臆斷。最重要的是，機器記憶和處理數據的精確度遠遠超出人類。而數據正以指數級增長。

(14)

假設裂隙之間互不連通、互不影響,HTI型裂隙介質中流體識別可以用KN/KT來指示:

(15)

其中，KN為裂隙法向柔度;KT為裂隙切向柔度。對于液體充填的裂隙介質，剪切模量μf=0，體積模量Kf與μ大致相差一個數量級，裂隙縱橫比通常很小,a/c?1，[(Kf+4/3μf)/μ]/(a/c)?1，此時ΔN≈0，ΔT與裂隙為干燥狀態時相同，流體因子KN/KT接近于0。

1.3 HTI介質各向異性反演實現過程

采用SA-PSO算法對HTI介質進行疊前AVO反演，基本思想可概括為:將待反演模型的上、下層的彈性參數作為種群中尋找最優解的粒子，通過位置公式進行迭代計算，選用不同的慣性因子和學習因子，使目標函數求解達到全局最小。具體流程如下:

(1)將模型確立為HTI介質模型;

(2)通過地震波反射系數近似公式計算出模型的PP波反射系數;

(3)確定HTI介質模型的輸入參數及待反演參數，構建目標問題的反演目標函數;

(4)將先驗信息與待反演參數輸入反演目標函數;

(5)輸入先驗地震數據信息或實測地震數據，利用SA-PSO算法尋找反演目標函數的最佳擬合;

(6)輸出待反演參數的最優解，預測儲層的相關流體因子。

假設待反演的各向異性參數符合粒子群分布，將反演的約束條件設為

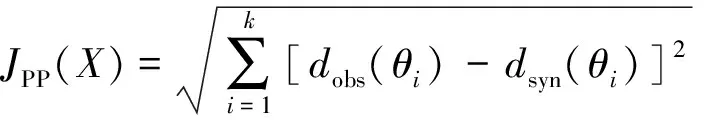
(16)

其中，X=(δ(v),ε(v),γ(v))為待反演的各向異性參數;i為地震記錄的道序號;dobs(θi)=[R(Sobs(θi))，I(Sobs(θi))]，dsyn(θi)=[R(Ssyn(θi))，I(Ssyn(θi))]，R和I分別為反射系數與子波褶積后復數的實部與虛部;θi為該道地震波對應的PP波入射角;Sobs(θi)

和Ssyn(θi)分別為HTI介質模型在PP波入射角為θi時的PP波反射系數序列與子波序列的褶積。

利用上述方法進行反演的技術流程如圖1所示。

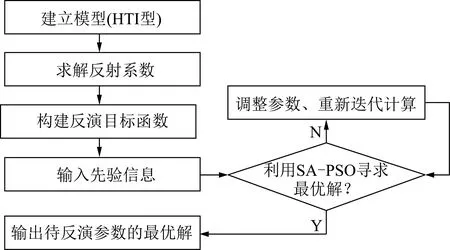
圖1 基于PSO-SA算法的反演流程Fig.1 Schematic diagram of inversion flow based on PSO-SA algorithm

2 模型試算

2.1 多層模型試算

建立一個4層的模型，從地表往下分別為第1，2，3，4層，橫向為400 m。其中，第1層為泥巖，厚度約為300 m;第2層為砂巖，含有垂向飽水裂隙，可近似為HTI型介質，層厚約為100 m;第3層為煤層，厚度約為10 m;第4層為泥巖，厚度約為300 m。模型對應的縱、橫波速度體如圖2(a)，3(a)所示，模型彈性參數和各向異性參數見表1。根據模型中第2層為基于HTI型飽水裂隙的假設，其各向異性參數ε(v)的值無限接近于0，δ(v)和γ(v)取值在0.1～0.3。

表1 理論模型的物性參數和各向異性參數Table 1 Physical and anisotropy parameters of the theoretical model

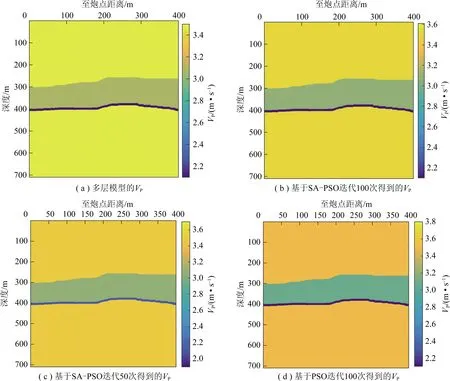
圖2 基于SA-PSO算法的模型VP反演剖面對比Fig.2 Comparison of model VP inversion profiles based on SA-PSO algorithm

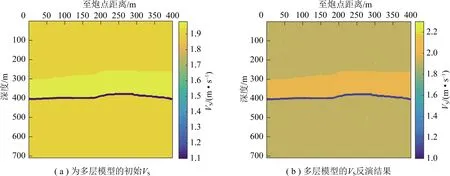
圖3 基于SA-PSO算法的多層模型VS反演剖面對比Fig.3 Model values and inversion results of S-wave velocity based on SA-PSO in the model

對多層模型設計目標函數并進行彈性參數和各向異性參數反演。首先，為證明本研究所提出的基于SA-PSO算法的科學性和有效性，對多層模型的VP進行不同迭代次數的SA-PSO反演和單一的PSO反演進行對比，結果如圖2所示。圖2(a)為模型的VP，對比圖2(b)可以看出，利用SA-PSO混合算法迭代次數較多(100次)時，尋優效果更穩定，得到的地層分異明顯，反演速度也與理論速度誤差較小。在圖2(c)中，使用SA-PSO迭代50次時，此時全局尋優尚不穩定，精度不高，所以出現細小噪點;圖2(d)為利用PSO反演，迭代次數達到100次時的結果，可以看出地層分異相較于圖2(c)效果稍好一些，參數區間也更精確一些，但是相比圖2(b)來說，反演結果不夠理想。綜上所述，利用SA-PSO反演時，由于SA-PSO反演克服了PSO的早熟現象，在迭代次數達到一定要求后反演精度高于單一的PSO反演，本模型中，當迭代次數達到100次時反演結果最好，得到的結果更穩定。

同時，對多層模型中的VS,ρ進行迭代次數為100次的SA-PSO反演，反演結果如圖3,4所示。分析圖3，4可以看出，從VP和VS的反演剖面來看，模型的地層能被清晰地分辨，反演結果較好。對于ε(v)，δ(v)，γ(v)，在初始模型中，由于除了砂巖層之外的其他地層均等效為各向同性介質，其各向異性參數均設置為0。在對砂巖層的各向異性參數進行反演時，抽取了橫向距離200 m處的數據進行試算，試算結果如圖5所示。在圖5中，對各向異性參數的反演值與理論各向異性參數對比，可以看出，反演值始終圍繞理論值波動，反演結果穩定，同時，ε(v)始終在0附近，這符合對砂巖層含有飽水裂隙的預設。多層模型的彈性參數和各向異性參數反演剖面均能指示地層，各向異性參數ε(v)出現在0附近，對裂隙流體的指示性強。

圖4 基于SA-PSO算法的多層模型ρ反演剖面對比Fig.4 Model values and inversion results of ρ based on SA-PSO in the model

針對抽取的橫向距離200 m處的試算結果，對其中縱向深度為350 m、橫向距離為200 m處的反演結果進行誤差定量分析，見表2。由表2可知，對于多層模型的多參數反演，ε(v)，VP的反演誤差最小，ρ，δ(v)的反演誤差略大。但整體來講，反演誤差都較小。

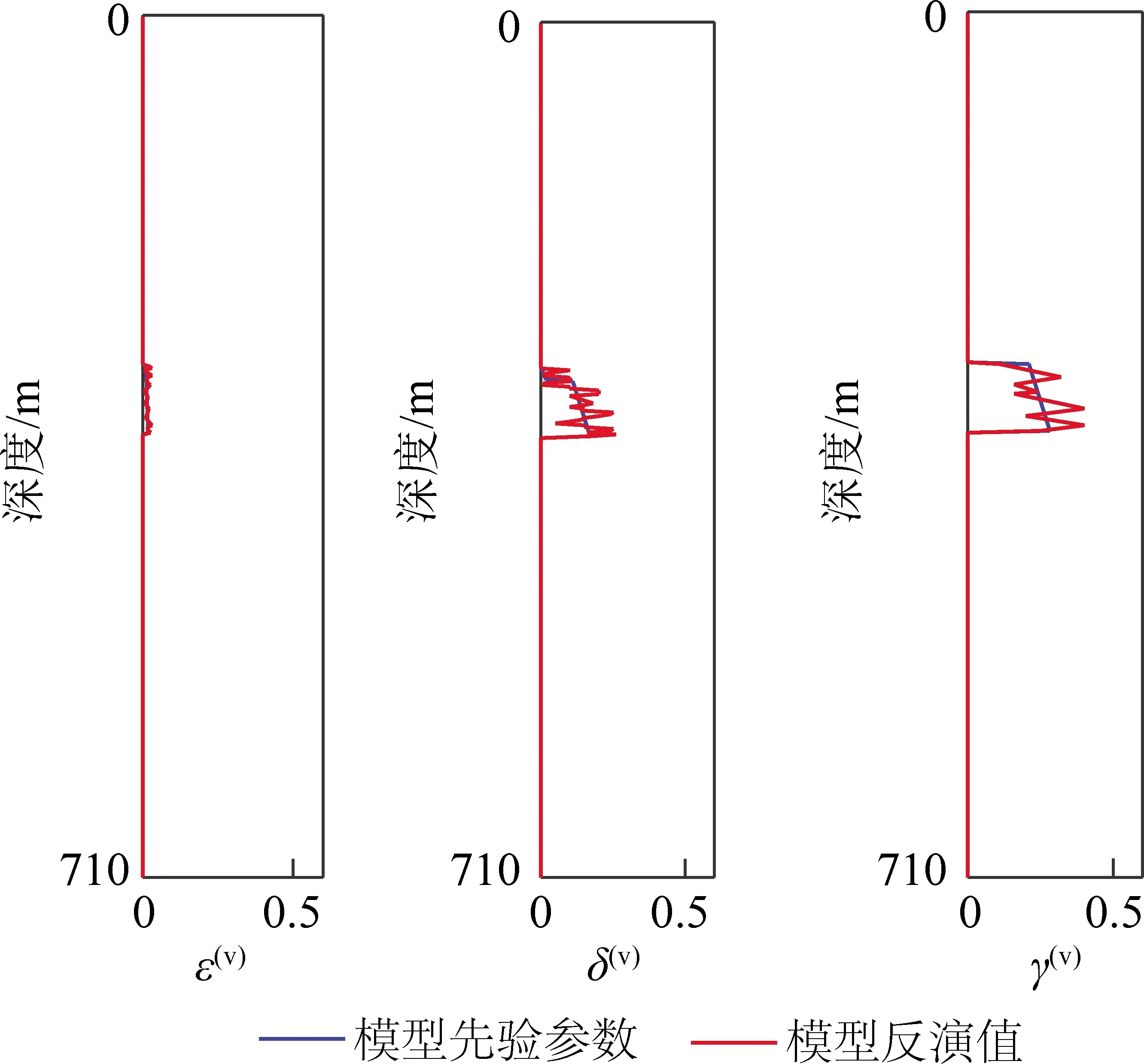
圖5 基于SA-PSO算法的多層模型各向異性參數 反演結果對比Fig.5 Model values and inversion results of anisotropic parameters based on SA-PSO in the model

同時，為討論該反演方法的抗噪性，依照正演流程計算模型的反射系數并采用40 Hz的雷克子波與反射系數進行褶積，生成不同入射角的角道集，并分別添加了信噪比(SNR)為5，10，20的高斯隨機噪聲，并針對各向異性層，分析不同信噪比數據的反演誤差(表3)。從表3來看，大致可以認為信噪比越高的數據反演誤差越小，在反演過程中也能夠越快收斂，但是在模型試算的結果中，信噪比與反演誤差并不完全負相關;即使在SNR=5時，角道集仍然能夠反映巖石物理模型的層位特征，在信噪比較低的地震記錄中也可以讀取有效信息，也就是說，信噪比較低的情況下，即使反演誤差稍大，但是對VP，ε(v)，δ(v)的反演結果仍然能滿足反演要求，反演算法具有一定的抗噪性。

表2 理論模型的反演誤差結果分析Table 2 Analysis of inversion error results of theoretical model

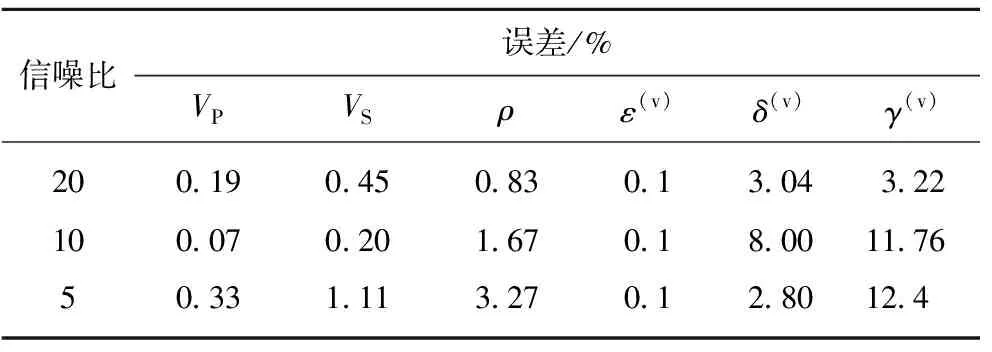
表3 有噪聲的理論模型反演結果誤差分析Table 3 Analysis of inversion error results of theoretical model with noise

利用模型的物性參數和各向異性參數反演值，根據多層模型縱向深度為301～399 m、橫向距離為100 m處的反演結果，利用SA-PSO算法對模型中砂巖層的流體指示因子KN/KT進行預測，結果如圖6所示。由圖6可知，利用抽取的部分模型物性參數和各向異性參數作為先驗值，得到的流體指示因子KN/KT均在0.4以下，最優值在0.12左右，符合裂隙飽和水時流體因子較小，接近于0的規律。

圖6 基于SA-PSO算法預測得到的流體因子Fig.6 Fluid factors predicted based on SA-PSO algorithm

2.2 改進的Marmousi2部分模型試算

原始Marmousi2模型如圖7所示,是復雜二維構造的地質-地球物理模型，屬于各向同性介質，本文選取紅框圈定的部分模型，并根據不同巖層的特性賦予各向異性參數:將含水砂巖之外的薄層作為各向同性介質，假定含水砂巖垂向裂隙發育，將其近似等效為HTI介質，且由于HTI介質在飽水裂隙發育情形下，各向異性參數ε(v)接近0，用于各向異性參數反演和裂隙流體因子的預測。采用主頻為50 Hz的雷克子波序列與HTI介質的PP波反射系數序列進行褶積，并對橫向距離為2 000 m、深度為 500～800 m的剖面，生成角道集如圖8所示。由圖8可知，反射同相軸大致能夠反映所選模型區域反射界面物性差異特征，反射振幅在裂隙附近呈現正極性，能量較弱。

圖7 Marmousi2模型及抽取區域示意[28]Fig.7 Marmousi2 model and the selected area[28]

圖8 Marmousi2改進模型抽取的角道集(2 000 m處)Fig.8 Synthetic angle gather in the Marmousi2 model (at the distance of 2 000 m)

采用本文研究的反演方法對這部分數據進行迭代次數為100次的SA-PSO反演，反演結果如圖9～12所示。分析圖9～11可以看出，對改進的Marmousi2部分模型反演得到VP，VS和ρ剖面，雖然反演值與理論值有一定誤差，但仍然能清晰反映所抽取的Marmousi2部分模型的地層變化規律，分層效果明顯，與實際模型基本吻合，反演結果較好。如圖12所示的各向異性參數反演結果曲線對比，各向異性參數ε(v)和γ(v)反演精度略高于各向異性參數δ(v)，對反演目標方程的敏感度相對較好。從多組反演結果與理論值的對比剖面可以看出，反演結果能夠較準確反映原始剖面形態特征，且與理論模型的擬合度高，誤差比較小。選取模型中橫向距離為2 000 m、深度為 630～660 m的區域，對流體指示因子KN/KT進行預測，所得結果如圖13所示，由于抽取的區域均為飽水裂隙區域，此時進行間隔采樣得到的流體因子就是PSO-SA算法中的“粒子”，“粒子們”最終迭代出最優結果(即紅色較大圓點)，因子粒子尋優時其初始值是隨機的，粒子的總數量與KN/KT的總數量一致,但粒子的取值與KN/KT的值不具有一一對應的關系，圖中所有粒子的值都小于1，與飽水裂隙中KN/KT的取值范圍一致。

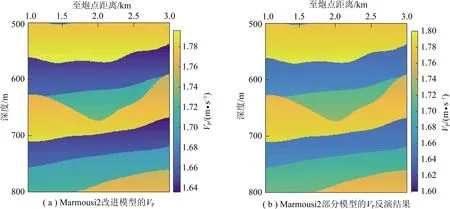
圖9 基于SA-PSO算法的 Marmousi2改進模型VP反演剖面對比Fig.9 Model values and inversion results of P-wave velocity based on SA-PSO in the Marmousi2 model

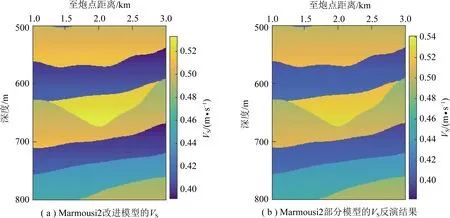
圖10 基于SA-PSO算法的 Marmousi2改進模型VS反演剖面對比Fig.10 Model values and inversion results of S-wave velocity based on SA-PSO in the Marmousi2 model

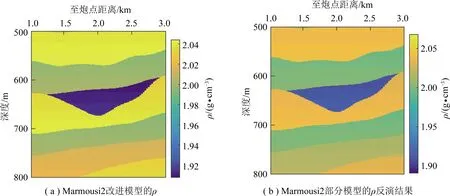
圖11 基于SA-PSO算法的 Marmousi2改進模型ρ反演剖面對比Fig.11 Model values and inversion results of ρ based on SA-PSO in the improved Marmousi2 model

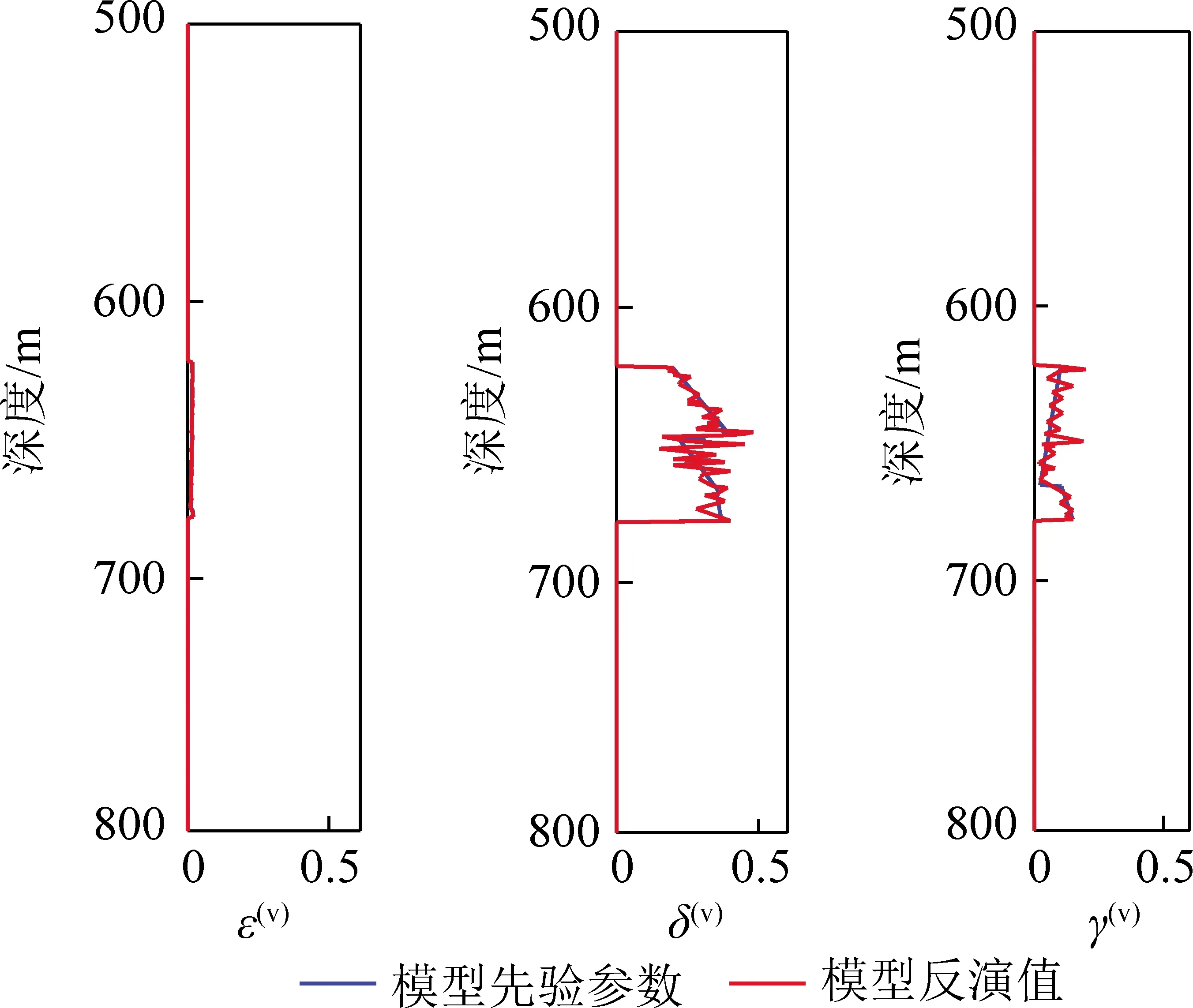
圖12 基于SA-PSO算法的Marmousi2改進模型各向異性 參數反演結果對比Fig.12 Model values and inversion results of anisotropic para- meters based on SA-PSO in the improved Marmousi2 model

圖13 基于SA-PSO算法的Marmousi2改進模型 流體因子預測Fig.13 Fluid factor prediction of Marmousi2 improved model based on SA-PSO algorithm

3 結 論

(1)綜合考慮粒子群算法快速收斂的特點和模擬退火的概率性跳出特性，通過對兩種算法的混合使用，實現了利用基于模擬退火的混合粒子群算法對HTI介質的AVO反演。該算法具有全局尋優能力較強，克服早熟現象，不易陷入局部極小值等優點。

(2)將基于SA-PSO算法的HTI介質疊前AVO反演應用于多層模型和復雜模型的反演計算中，反演結果與理論模型擬合較好，計算結果穩定，抗噪性較好，反演精度較高。

(3)根據裂隙含水時流體指示因子KN/KT較小的特點，并借助HTI介質各向異性反演，通過建立裂隙流體因子KN/KT與各向異性參數的關系，可實現流體因子預測。