一類二階非線性常微分方程組邊值問題解的存在唯一性

王 丹, 李永祥

(西北師范大學數學與統計學院, 蘭州 730070)

1 引 言

本文討論二階非線性常微分方程組邊值問題

(1)

解的存在唯一性, 其中非線性函數f,g:[0,1]×R×R→R連續.作為生物種群的常用數學模型,該問題在生物數學等領域有重要應用,不少作者對該問題正解的存在性進行過研究[1-10].常用研究方法主要有文獻[1,5,7-10]中的錐上的不動點指數理論, 文獻[2-3]中的錐上不動點定理, 以及文獻[4,6]中的單調迭代求解方法，等.

1993年，Fink和Gatica[1]運用錐上的不動點指數理論, 在f與g嚴格單調條件下獲得了邊值問題

非負解的存在性. 后來, Ma[2]將上述條件弱化為單調條件, 通過舉例得到了問題(2)新的非負解的存在性結論. 文獻[3]研究了邊值問題

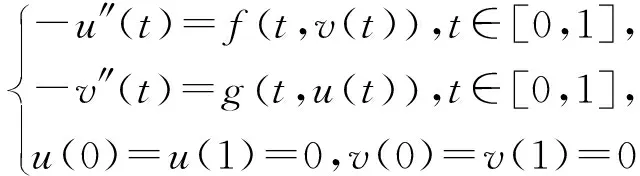
(3)

(該問題的非線性項都是非負的)，在超線性或次線性的條件下獲得了正解的存在性. 在上述文獻中, 系統正解的存在性均被轉化為乘積空間中單錐上相應全連續映射的不動點的存在性.此外，Cheng等[7-10]建立了乘積錐上不動點指數的乘積公式 (見文獻[7]中定理2.1), 運用不動點指數的乘積公式在一些超(次)線性假設下獲得了幾類不同形式的邊值問題正解的存在性, 推廣了以上結論.

鑒于以上文獻都在非線性項f與g各自獨立的條件下討論方程組非負解或正解的存在性，本文則不假設f與g非負, 在f(t,x,y)與g(t,x,y)相關聯的不等式條件下運用Leray-Schauder不動點定理獲得問題(1)解的存在唯一性. 本文的主要結果如下：

定理1.1設f,g:[0,1]×R×R→R連續.若f,g滿足下列條件：

(H1) 存在常數a,b≥0使得a+b<π2及c>0, 使得

f(t,x,y)x+g(t,x,y)y≤

ax2+by2+c,(t,x,y)∈[0,1]×R×R

(4)

則問題(1)至少存在一個解.

加強定理1.1的條件(H1)后, 則有如下存在唯一性結果：

定理1.2設f,g:[0,1]×R×R→R連續.若f,g滿足下列條件：

(H2) 存在常數a,b≥0使得a+b<π2,

(f(t,x2,y2)-f(t,x1,y1))(x2-x1)+

(g(t,x2,y2)-g(t,x1,y1))(y2-y1)≤

a(x2-x1)2+b(y2-y1)2

(5)

其中(t,xi,yi)∈[0,1]×R×R,i=1,2, 則問題(1)的存在唯一解.

2 主要結果的證明

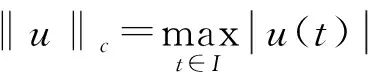
記H1(I)={u∈C(I)|u在I上絕對連續, 且u′∈L2(I)}.

設X,Y分別為范數是‖·‖X,‖·‖Y的Banach空間. 以X×Y表示X與Y的乘積空間按范數‖(x,y)‖=max{‖x‖X,‖y‖Y}構成的Banach空間.

證明 因正弦函數系{sinkπt|k=1,2…}為L2(I)中的完備直交系, 故u可展為正弦級數

其中

且有Parseval等式

另一方面, 余弦函數系{coskπt|k=1,2…}也為L2(I)中的完備直交系, 故u′可展為余弦級數

其中

且有Parseval等式

因而引理2.1成立.

定理1.1的證明 熟知, ?h∈C(I), 線性二階邊值問題

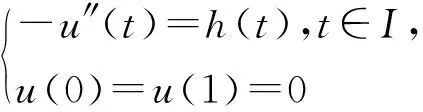
(6)

存在唯一解

其中

為相應的Green函數. 作積分算子A:C(I)×C(I)→C(I)×C(I)為

則A:C(I)×C(I)→C(I)×C(I)為全連續算子, 且問題(1)的解(u,v)等價于算子A的不動點. 我們對A應用Leray-Schauder不動點定理,以證明A有不動點. 為此，考查方程簇

(u,v)=λA(u,v),0<λ<1

(7)

設(u,v)∈C(I)×C(I)為方程簇(7)中某個λ∈(0,1)對應的方程的解.則

(8)

按線性方程解的Green函數表示, (u,v)∈C2(I)×C2(I)滿足方程

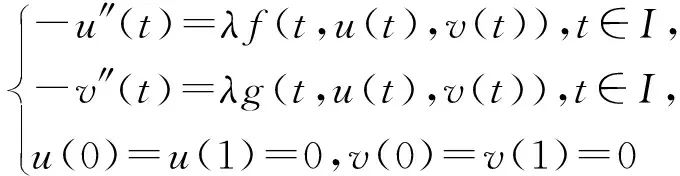
(9)

將方程(9)的第一式和第二式的兩邊分別同乘以u(t)和v(t), 兩式相加, 由條件(H1)可得

-u″(t)u(t)-v″(t)v(t)=λf(t,u(t),

v(t))u(t)+λg(t,u(t),v(t))v(t)≤

λ(au2(t)+bv2(t)+c)≤

au2(t)+bv2(t)+c,t∈I.

上式在I上積分, 左邊利用分部積分和方程(9)的邊界條件得

由引理2.1,

從而有

所以

因此, ?t∈I, 有

所以

故

即方程簇(7)的解集在C(I)×C(I)中有界. 由Leray-Schauder不動點定理,A在C(I)×C(I)中有不動點, 該不動點為問題(1)的解.

f(t,x,y)x+g(t,x,y)y=(f(t,x,y)-

f(t,0,0))x+(g(t,x,y)-g(t,0,0))y+

f(t,0,0)x+g(t,0,0)y≤ax2+by2+

|f(t,0,0)x|+|g(t,0,0)y|≤ax2+by2+

C0|x|+C0|y|=ax2+by2+

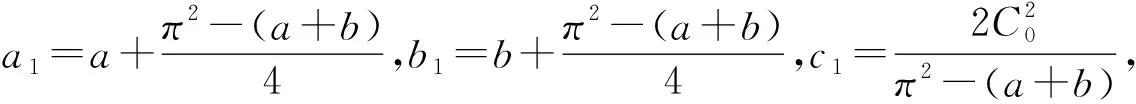
f(t,x,y)x+g(t,x,y)y≤

a1x2+b1y2+c1,(t,x,y)∈I×R×R.

再證解的唯一性. 設(u1,v1),(u2,v2)∈C2(I)×C2(I)為問題(1)的兩個解.則有方程

(10)

及

(11)

將方程(11)第一式與方程(10)第一式相減, 方程(11)第二式與方程(10)第二式相減, 得

-(u″2(t)-u″1(t))=f(t,u2(t),v2(t))-

f(t,u1(t),v1(t)),t∈I

(12)

-(v″2(t)-v″1(t))=g(t,u2(t),v2(t))-

g(t,u1(t),v1(t)),t∈I

(13)

將方程(12)兩邊同乘u2(t)-u1(t), 方程(13)兩邊同乘v2(t)-v1(t), 兩式相加, 由條件(H2)得

-(u″2(t)-u″1(t))(u2(t)-u1(t))-

(v″2(t)-v″1(t))(v2(t)-v1(t))=

(f(t,u2(t),v2(t))-f(t,u1(t),

v1(t)))(u2(t)-u1(t))+(g(t,u2(t),

v2(t))-g(t,u1(t),v1(t)))(v2(t)-

v1(t))≤a(u2(t)-u1(t))2+

b(v2(t)-v1(t))2,t∈I.

上式在I上積分, 左邊利用分部積分和方程(10)(11)的邊界條件得

即

3 例

例3.1考慮如下二階微分方程組

方程(14)相應的非線性項為

f(t,x,y)=3x-x3y2+sinπt,g(t,x,y)=

-x2y+6y-2y3+2sinπt

(15)

因為f與g不是非負的, 文獻[1-10]的結果對問題(14)不適用.

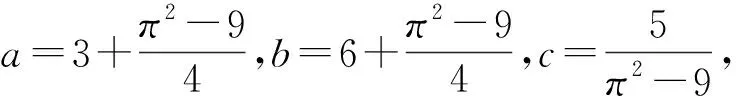
f(t,x,y)x+g(t,x,y)y=3x2-x4y2+

xsinπt-x2y2+6y2-2y4+2ysinπt≤

3x2+6y2+xsinπt+2ysinπt≤3x2+

6y2+|x|+2|y|=3x2+6y2+

ax2+by2+c.

因而f(t,x,y)與g(t,x,y)滿足條件(H1). 由定理1.1知方程(14)有解.

例3.2考慮如下二階微分方程組

方程(16)相應的非線性項為

f(t,x,y)=5x-x3-y+1,g(t,x,y)=

x+4y-y5+t

(17)

下面驗證f(t,x,y)與g(t,x,y)滿足條件(H2).?(t,xi,yi)∈[0,1]×R×R,i=1,2. 由(17)式可得

(f(t,x2,y2)-f(t,x1,y1))(x2-x1)+

(g(t,x2,y2)-g(t,x1,y1))(y2-y1)=

(x2-x1)+((x2-x1)+4(y2-y1)-

對函數-x3在x1與x2之間應用微分中值定理得

對函數-y5在y1與y2之間也應用微分中值定理得

結合以上諸式有

(f(t,x2,y2)-f(t,x1,y1))(x2-x1)+

(g(t,x2,y2)-g(t,x1,y1))(y2-y1)=

5(x2-x1)2-3ξ2(x2-x1)2+

4(y2-y1)2-5η4(y2-y1)2≤

5(x2-x1)2+4(y2-y1)2.

因而f(t,x,y)與g(t,x,y)滿足條件(H2). 由定理1.2知方程(16)有唯一解.