雙頻投影條紋相位展開方法的改進

雷經發，陳志強，張 淼，孫 虹，李永玲

（1.安徽建筑大學 機械與電氣工程學院，安徽 合肥230601；2.工程機械智能制造安徽省教育廳重點實驗室，安徽 合肥230601；3.安徽省仿真設計與現代制造工程技術研究中心，安徽 黃山245041）

1 引 言

結構光三維測量具有非接觸、全場性和高精度等優點［1-4］。其關鍵的核心問題之一是光柵相位場的解算，尤其是高效率和高可靠性的展開復雜形面的條紋圖像相位主值［5-6］。目前，相位展開方法可分為空域法和時域法兩大類。投影多頻條紋根據外差原理進行相位展開的方法是時域相位展開法的典型代表之一［7］。此方法對被測目標表面的顏色不敏感，可以準確地展開復雜物體表面的相位主值，具有計算過程穩定、實用性強的優點，因而得到了廣泛的應用［8-9］。

國內外很多學者對利用外差原理進行相位展開的方法進行了大量的研究。GUO等提出了投影雙頻條紋，分別建立高頻或低頻光柵相位與高度映射查找表的方法，實現了三維面形的快速高精度測量［10］。DONG等利用遺傳算法補償隨機相位以增強外差信號的方法，在低信噪比環境下依然具有良好的解相效果［11］。WANG等采用先對條紋圖像進行小面積自旋濾波處理再用外差解相的方法，進一步提升了算法的性能［12］。郭進等投影三種不同頻率的條紋圖像，使用三頻外差原理展開相位主值的方法，很大程度上解決了周期次數非正常跳變的問題，降低了絕對相位的跳躍性誤差［13］。陳松林等提出了一系列約束條件，進一步改進了三頻外差相位展開法，解出的絕對相位光滑無跳躍［14］。隨著研究的深入，涌現了很多有效的基于多頻外差原理的相位展開方法，但這些方法都或多或少增加了輔助條件，復雜程度有所增大。

本文針對投影雙頻條紋在根據外差原理進行相位展開時絕對相位存在跳變性誤差的問題，利用解相過程已有的必要結論和結果，先解出條紋級數小數部分的計算值和實際值，再結合相位主值自身的誤差對相位展開算法進行了改進，以實現絕對相位校正。實驗結果表明，改進的方法基本不增加額外的工作量，簡單可靠，可以較好地校正絕對相位的跳躍性誤差，具有實際應用價值。

2 外差解相原理

投影雙頻光柵條紋根據外差原理進行相位主值展開的方法的理論知識和公式推導過程參閱文獻［15］和［16］。

若設不同頻率光柵的條紋級數為ni，則可將條紋級數值分為整數部分N i與小數部分Δni相加，即有：

因此，若設各頻率條紋的相位主值為φi，則條紋級數的小數部分與相位主值有如下關系：

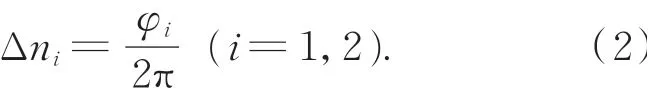
本文統一將相位主值解到[0，2π]區間。若設各頻率條紋的光柵節距為p i，則根據條紋疊柵特性可知疊柵后的條紋級數為同一級別，即其取值區間為[m，m+1]。則可分別求出兩種頻率投影光柵的條紋級數ni，n2如下式所示：

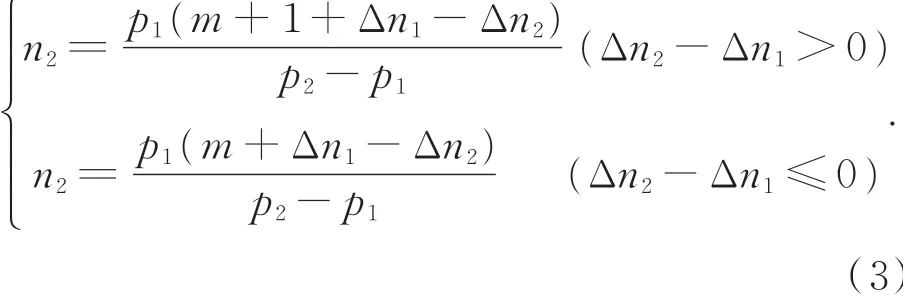
同理可解算另一個條紋級數。一般將解出的條紋級數進行向下取整得到其整數部分，并作為周期次數進行相位展開，得到：

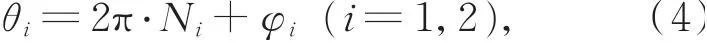
式中θi為各頻率條紋的絕對相位值。

3 改進方法的原理

3.1 投影圖案的相位初值設定

在不考慮實時測量的情況下，應當優先使用相移法提取相位主值。四步相移法具有提取相位主值精度高、實用性強等優點［17-18］，因此本文采用四步相移法提取相位主值。

投影雙頻條紋圖案中，某一頻率下一組4幅相移圖案可用公式表示如下：

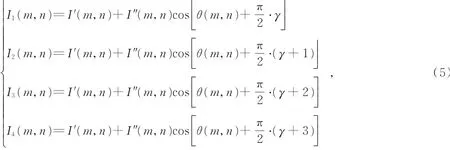
式中：γ∈Z，(m，n)表示圖案中的像點坐標，I'(m，n)表示背景光強，I″(m，n)表示調制強度，θ(m，n)表示條紋圖案的相位場。

當γ=0時，式（5）為通常的四步相移法，即投影的第一幅相移圖案的相位初值為零，提取相位主值后，利用外差原理展開相位不僅會出現跳躍性誤差，還會出現階梯現象，如圖1中藍線所示（彩圖見期刊電子版）；當γ=?2時，投影的第三幅相移圖案的相位初值為零，提取相位主值后，利用外差原理展開的絕對相位僅出現了跳躍性誤差，如圖1中紅線所示，這是改進方法需要解決的問題。因此，本文編制相移投影圖案時取γ=?2，即投影的第三幅相移圖案的相位初值為零。同時，利用四步相移法提取相位主值時要考慮反正切函數的象限問題，將相位主值的取值區間擴展到[0，2π]［19］。

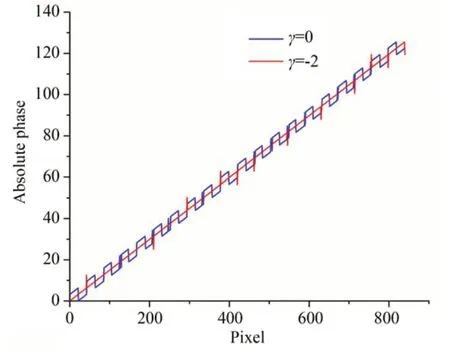
圖1 相位初值對應的絕對相位Fig.1 Absolute phase corresponding to phase initial value

3.2 調整周期次數非正常跳變

根據式（3），不妨設：

實際上，Δn12為雙頻條紋疊柵后形成的虛擬光柵的條數級數的小數部分。令：

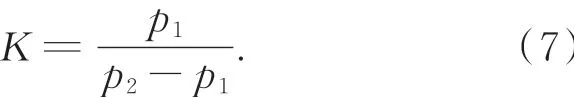
同時，假設疊柵后的虛擬光柵相位場的初始值為零，即m=0。聯立式（6）和式（7），則式（3）可改寫為：

式中K為常量。根據相位展開公式（4）可知，需對條紋級數進行向下取整操作，即：

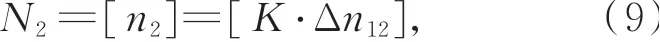
式中符號［］表示向下取整運算。深入分析易知：理論上，當虛擬條紋級數的小數部分Δn12為1K的整數倍時，即Δn12=c K，c=1，2，3，4…，N2會發生正常跳變，即隨著c變大，其逐步加1。但實際情況是，在理論值Δn12接近或等于c K時，由于誤差等影響，實際的Δn12值可能會發生變化，導致條紋級數的整數部分，即周期次數發生不正常的跳變，如圖2所示，最終的絕對相位也會出現跳躍性誤差。

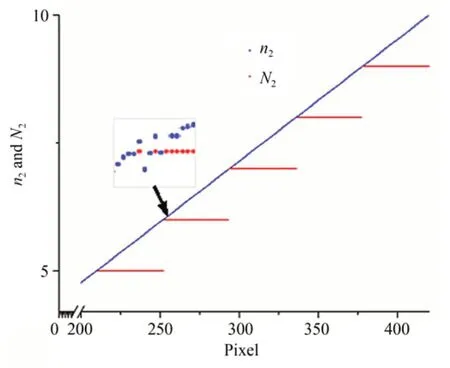
圖2 周期非正常跳變示意圖Fig.2 Schematic diagram of abnormal periodic jump

根據式（2）和式（4）可知，理想環境下，利用外差原理解出的條紋級數的小數部分的計算值Δn2c應與依據當前相位主值計算出的小數部分的實際值Δn2r相等。小數部分的計算值為：

而實際上由于相位主值自身誤差等原因，兩者并不相等。根據以上分析可知，若周期次數發生向上或向下跳變，小數部分的計算值與實際值之差的絕對值必定會大于某一值，且此值與相位主值自身誤差緊密相關，可稱為閾值T。

若已知各頻率條紋的相位主值的自身誤差，各頻率條紋級數的小數部分可根據公式（2）算出，因此可將相位主值自身誤差轉化為小數部分誤差。設Δn1的誤差為δ1，Δn2的誤差為δ2，則Δn12的 誤 差 為(?δ1?δ2，δ1+δ2)，由 此 閾 值T為：

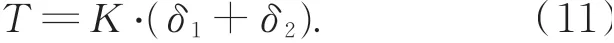
文獻［20］指出，未校正過的四步相移法提取相位主值的誤差不超過0.08 rad，且K值可根據光柵節距算出，則式（11）中所有量均為已知量。

綜上，調整周期非正常跳變的方法可歸納如下：

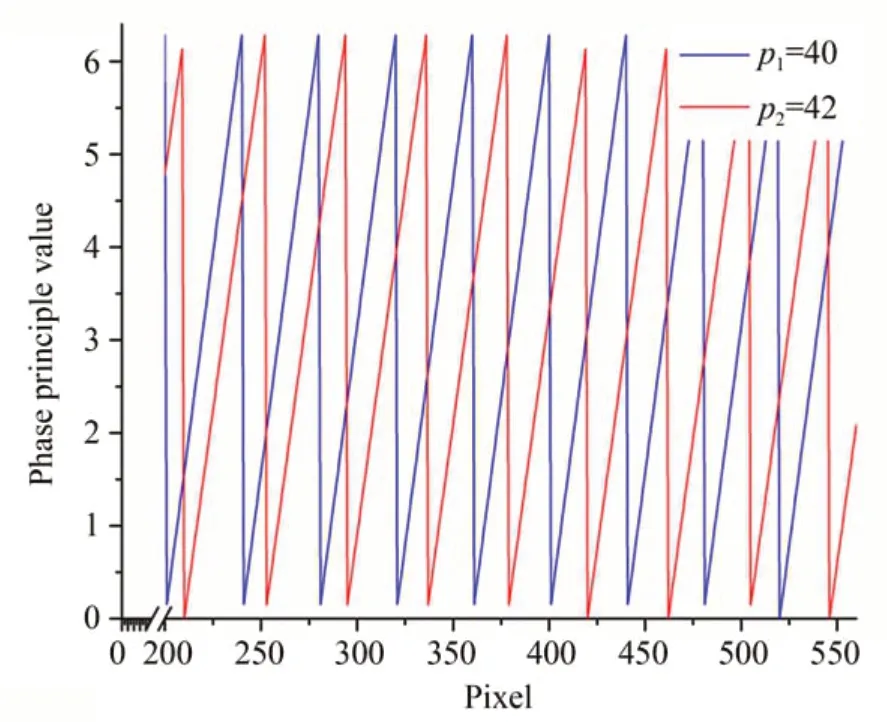
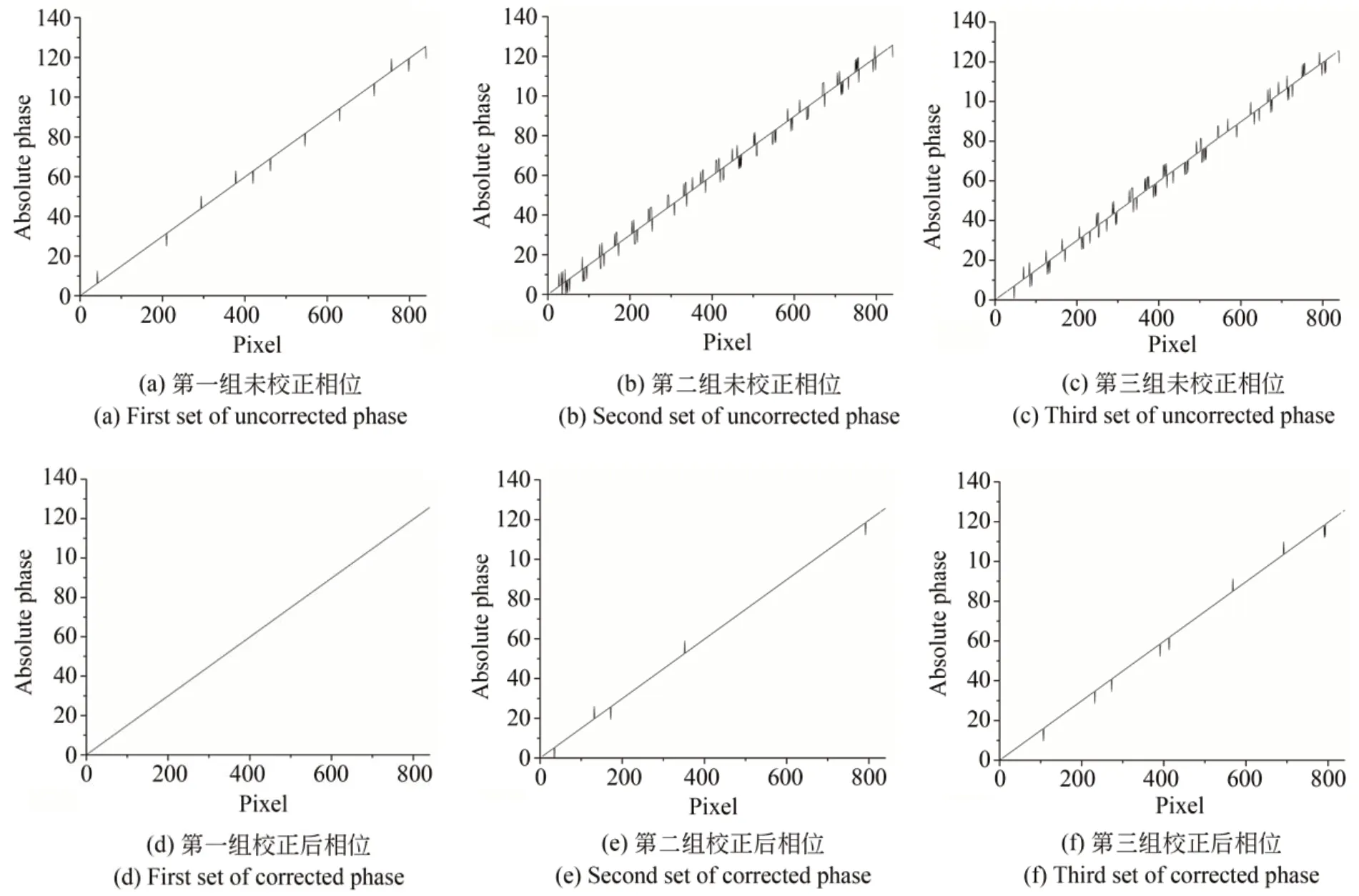
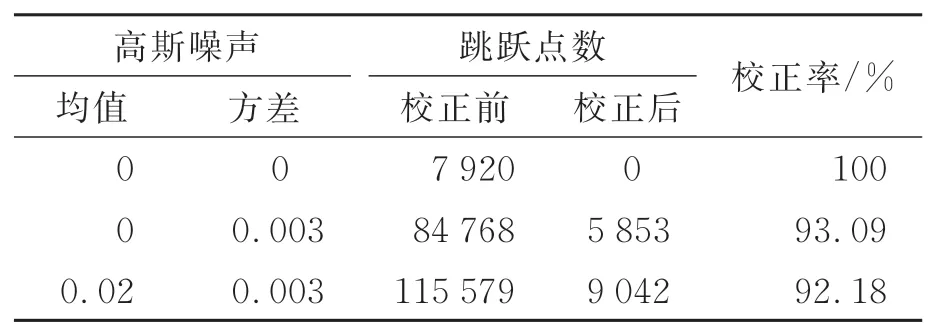
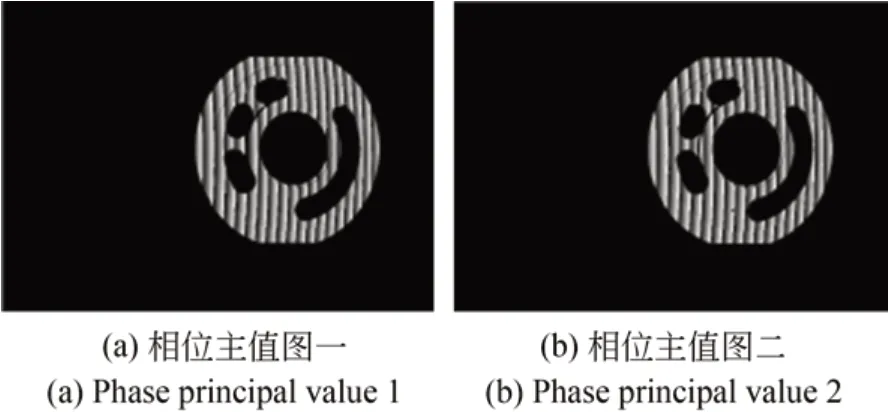
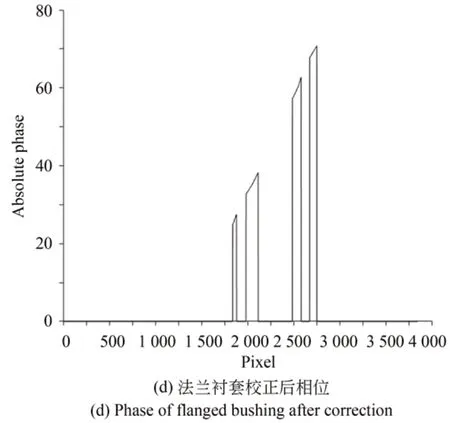
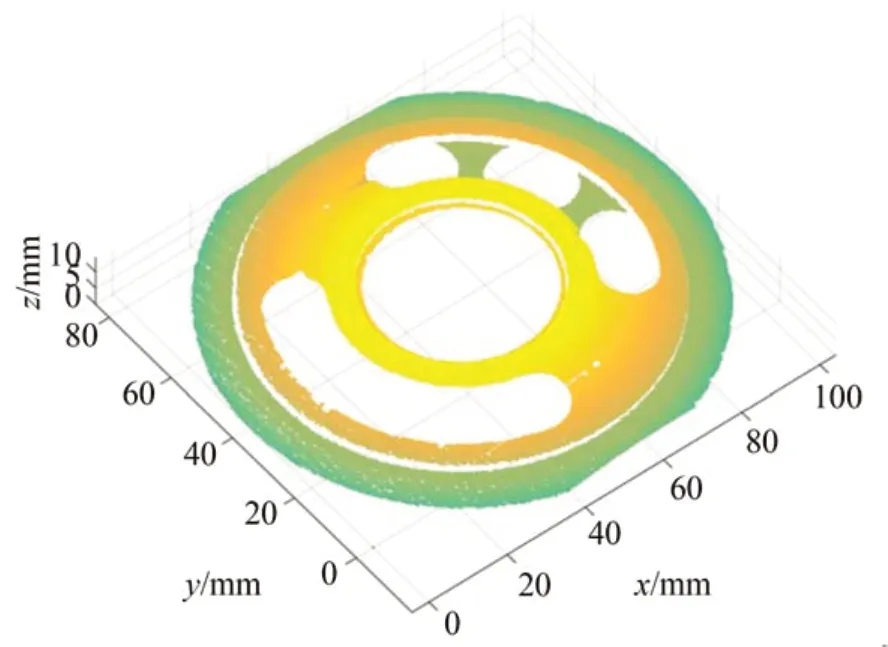
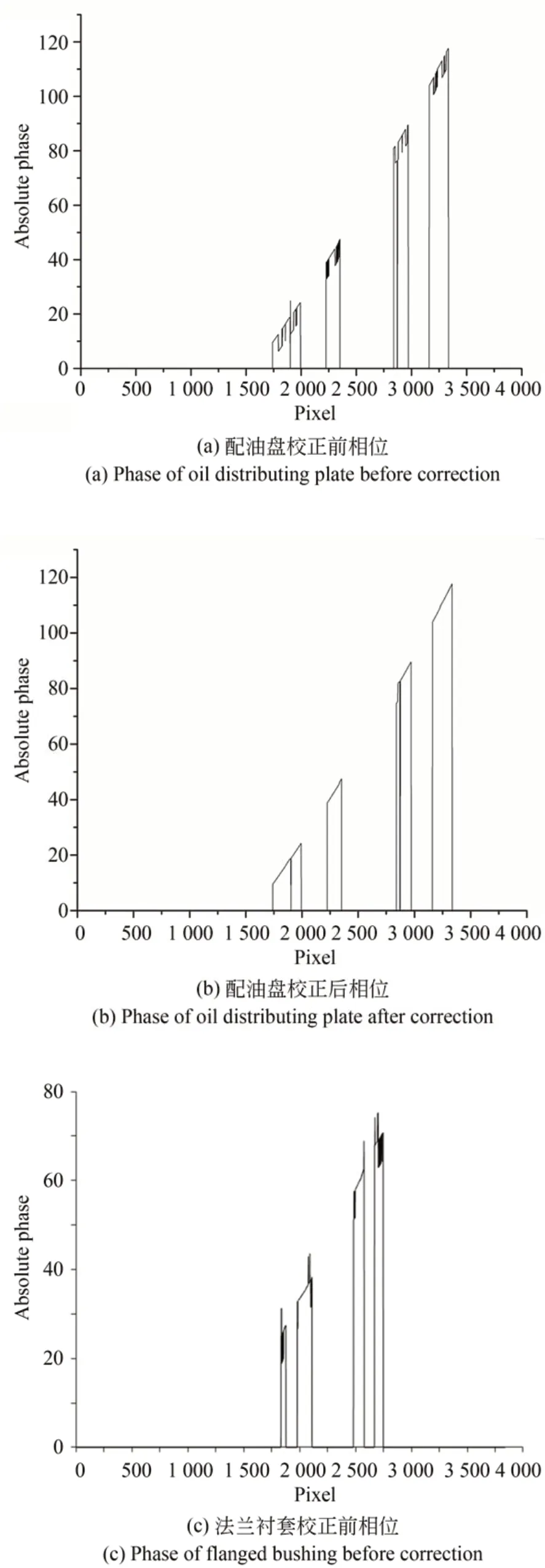
（1）若|Δn2r?Δn2c|

（2）若|Δn2r?Δn2c|≥T，且Δn2r?Δn2c>0，則周期次數出現向上跳躍，將此時周期次數值減一即可；

（3）若|Δn2r?Δn2c|≥T，且Δn2r?Δn2c≤0，則周期次數出現向下跳躍，將此時周期次數值加一即可。

根據上述分析可知，光柵節距較大的條紋的相位主值在利用外差原理直接展開時不容易出現跳躍性誤差。

4 實驗與結果分析

4.1 仿真實驗

為驗證改進方法的正確性與可靠性，仿真了光柵節距分別為40 pixel和42 pixel的兩組四步相移條紋圖案，其分辨率為720×840 pixel。根據四步相移法分別提取出兩組各自的相位主值，如圖3所示（彩圖見期刊電子版）。

圖3 雙頻條紋的相位主值Fig.3 Phase principal values of dual-frequency fringes

作為對比，在原始相移圖中加入了不同的高斯噪聲，再利用雙頻外差原理展開相位主值，并使用本文提出的改進方法校正絕對相位，判定閾值具體設為T=0.509，如圖4所示。

圖4 表示在不同均值和方差的高斯噪聲條件下3組實驗中絕對相位校正前后的分布情況。隨后，統計各組絕對相位圖中校正前后的跳躍性誤差像素數，如表1所示。

圖4 不同高斯噪聲下的絕對相位Fig.4 Absolute phases with different Gaussian noises

表1 跳躍性誤差點數Tab.1 Jumping error points

根據圖4和表1可以看出，改進方法可極大程度地降低跳躍性誤差點數，校正率可到90%以上，且加入噪聲時也會改變相位主值的自身誤差，但改進方法仍然表現出很好的校正結果，具有一定的抗噪性。

4.2 真實實驗

為驗證改進方法的實際應用價值，搭建了圖5所示的測量系統。圖像采集裝置為康耐視工業相機，投影裝置為騰聚DLP結構光發生器，兩者光心相距約20 cm，投影裝置光心距離物體約40 cm。

圖5 雙頻投影條約相位展開改進方法測量系統Fig.5 Measurement system for improved unwapping method of dual-frequency projection fringe

控制投影裝置投射與仿真實驗中設定值一樣的相移圖案于被測物表面，并使用相機同步采集，利用四步相移法提取相位主值的雙頻投影光柵需采集8幅圖像。以一個配油盤和一個法蘭襯套作為被測物。其中，測量配油盤時所采集到的兩種頻率各自的第一幅相移圖如圖6所示。根據四步相移法提取出兩種頻率條紋各自的相位主值，如圖7所示。

圖6 不同頻率的相移圖Fig.6 Phase shift images at different frequencies

圖7 不同頻率的相位主值圖Fig.7 Phase principal value images at different fre?quencies

利用外差原理展開相位主值，并用本文改進方法進行校正，閾值設定與仿真時一致，校正前后的絕對相位值如圖8所示。圖8（a）~和8（b）為配油盤校正前后的絕對相位值，取其相位圖中橫穿樣件中心的第1 500行數據進行對比；圖8（c）和8（d）為法蘭襯套的法蘭面校正前后的絕對相位值，取其相位圖中橫穿樣件中心的第1 620行數據進行對比。

由圖8可知，未校正前絕對相位存在跳躍性誤差，而校正后展開的相位光滑無跳躍。使用標定好的測量系統，利用校正后的相位解出配油盤和法蘭襯套的三維點云，分別如圖9和圖10所示。

圖8 校正前后的絕對相位值Fig.8 Absolute phase values before and after correction

圖9 配油盤元件的三維點云Fig.9 Three-dimensional pointcloud of oil distribution pan

圖9 是利用配油盤表面的相位場和測量系統定標參量解出的三維點云數據，而圖10是依據法蘭襯套的法蘭面的相位值解出的三維點云數據，點云模型特征與元件表面的絕對相位息息相關。被測物三維點云曲面或平面的平整性也可說明校正后的相位跳躍性誤差得到了較好的抑制，改進方法有效可靠。

圖10 法蘭襯套的三維點云Fig.10 Three-dimensional point cloud of flanged bushing

5 結 論

本文針對投影雙頻條紋利用外差原理展開相位主值時會出現跳躍性誤差的問題，基于解相過程，結合相位主值自身誤差為條紋級數的小數部分的計算值和實際值之差設定一閾值，進而調整周期次數，消除非正常跳變。實驗結果表明，在一定噪聲和實際環境下，改進方法對絕對相位跳躍性誤差的校正率可以達到90%以上，滿足實際應用需求。

然而，投影雙頻光柵由于疊柵要求存在測量范圍狹窄和投影條紋過粗等缺陷，后續會針對該問題展開進一步研究。