棉纖維蠕變與應力松弛行為分析

李 勇 李 健 雷福祥 張洪洲 陳曉川

（1.塔里木大學，新疆阿拉爾，843300；2.東華大學，上海，201620）

原棉是重要的紡織原材料，其結構蓬松、纖維間組織松散，給其初加工、儲運環節帶來不便。在生產加工過程中，原棉需要不斷進行機械壓縮、開松。棉纖維集合體材料具有典型的黏彈性力學性能，受載荷作用易蠕變、松弛。

國內外諸多研究者用經典理論、模型研究纖維材料的蠕變與應力松弛行為。DUNLOP J I［1］構建了纖維集合體體積變化模型（庫侖模型），其可解釋壓縮過程中纖維滑移、變形滯后和不可回復等現象。YAMAGUCHIY［2］測試了棉、毛、絲、麻等纖維的拉伸蠕變性能，指出纖維拉伸蠕變與應力和時間相關。王旭等［3］測試了麻賽爾纖維的蠕變和應力松弛性能，表明麻賽爾纖維松弛現象不明顯，蠕變現象更為明顯。陳康等［4］利用萬能試驗機測試了聚酯工業絲的蠕變性能，并提出了蠕變載荷與蠕變斷裂的預測方法。GAO Xiaoping等［5］研究了地毯紗線在動態加載后的蠕變行為，利用標準線性模型、四單元模型和黏彈性模型等力學模型獲得蠕變公式，進行非線性擬合獲得蠕變試驗數據，預測紗線蠕變伸長率。ASAYESH A等［6］用黏彈性模型分析了平紋織物蠕變力學性能，發現紗線密度增加，織物蠕變量減小。DANIL CHUK E L［7］研究了機織物蠕變性，非線性黏彈模型可表達聚合物織物的蠕變性。NAKAJIMA Chie和YONEDA Morihiro等［8-9］研究了高濕度條件下滌綸、銅氨纖維和萊賽爾纖維填料的壓縮蠕變和應力松弛行為，用經驗公式模擬各類填料的蠕變和應力松弛行為。

作為典型的黏彈性材料，棉纖維的蠕變與松弛力學行為與其加工應用息息相關，但仍未深入分析。本研究以棉纖維為研究對象，依據棉纖維的壓縮蠕變與應力松弛特性建立黏彈塑性本構模型。不同載荷下測試棉纖維的蠕變與應力松弛曲線，分析壓縮載荷與其力學指標之間關系，為原棉的生產加工環節提供一定理論指導。

1 試驗部分

1.1 材料與儀器

原料為新疆阿拉爾市新陸中37手摘原棉，原棉提取于新疆新越絲路有限公司。FA 1104型電子天平（上海安亭科學儀器廠），FSR400型薄膜壓力傳感器（Interlink Electronics），有線薄膜壓力傳感軟件（安徽威科電子有線公司），DSCa-01型數字式小樣梳棉機（天津嘉誠機電設備有限公司），圓盤取樣器（溫州大榮紡織儀器有限公司）。

1.2 制樣

為使棉纖維取向一致，原棉經小樣梳棉機梳理成原棉層，再利用圓盤取樣器切出直徑90 mm的原棉圓片，逐層疊加，制得棉樣（高度30 cm，重量160 g）。

1.3 蠕變回復試驗

棉樣放置于載樣臺上（為了防止棉樣受壓滑移，載樣臺固裝直徑為8 mm的定桿，棉樣套在定桿上），不銹鋼重塊加壓棉片進行蠕變試驗（室內溫度19℃～25℃，相對濕度45%～57%），如圖1（a）所示。每隔一定時間，薄膜壓力傳感器采集棉纖維內部壓力值，記錄棉纖維高度值。蠕變試驗結束，即卸除棉纖維壓力。每隔一定時間記錄棉纖維回復量。蠕變時間600 h，回復時間400 h。對棉纖維依次施加20 N、40 N、60 N、100 N、200 N、400 N、600 N的重塊進行蠕變回復試驗。

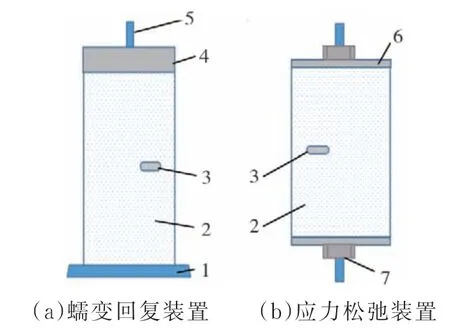
圖1 試驗裝置

1.4 應力松弛試驗

棉樣由兩片不銹鋼圓盤（不銹鋼圓盤由絲桿和螺母組件固定，調節兩片不銹鋼圓盤的間距可獲得不同應變的棉纖維）夾持進行松弛試驗（室內溫度19℃～25℃，相對濕度45%～57%），如圖1（b）所示。薄膜壓力傳感器采集棉纖維內部壓力值，每隔一定時間記錄棉纖維壓力值。棉纖維應變依次為76%、79%、81%、83%，分別進行應力松弛試驗。

2 蠕變和松弛行為

棉纖維的蠕變回復曲線（施加20 N壓力）如圖2所示。

圖2 棉纖維蠕變回復曲線

圖2中，棉纖維的蠕變回復過程分為5個階段，OA段為瞬時變形、AB段為減速蠕變（應變速率隨時間增加而降低）、BC段為穩態蠕變（應變量趨于穩定）［10］、CD段為瞬時回復、DE段為緩慢回復。瞬間壓力作用，纖維網快速屈曲變形，纖維間空隙減小，棉纖維展現出彈性。隨著壓力持續作用，棉纖維間不斷滑移致密，其展現出黏彈性變形和黏塑性變形。各階段應變依次定義為初始蠕變量εA、減 速 蠕 變量εBA（εBA=εB-εA）、穩態 蠕 變 量εCB（εCB=εC-εB）、急彈回復量εCD（εCD=εC-εD）、緩彈回復量εDE（εDE=εD-εE）和塑性蠕變量εE。

棉纖維的應力松弛曲線（應變為76%）如圖3所示。圖3中，棉纖維應力值隨時間增加逐漸降低。

圖3 棉纖維應力松弛曲線

3 黏彈性模型分析

棉纖維是高蓬松態的黏彈性材料，可通過彈簧和黏壺的組合表達其力學形態。黏彈性物料的蠕變多采用Burgers模型描述，本研究采用四元件模型模擬棉纖維的蠕變行為；黏彈性物料的應力松弛多采用Maxwell模型描述，本研究采用五元件模型模擬棉纖維的應力松弛行為。

3.1 蠕變回復模型

四元件模型如圖4所示［11］。圖4中E1、E2指彈簧的彈性模量，η1、η2指黏壺的黏滯系數。在外力作用下，彈簧E1瞬間響應，表征彈性變形；彈簧E2與黏壺η1并聯逐漸響應，表征黏彈性變形；黏壺η2響應，表征塑性變形。

圖4 四元件模型

四元件模型的蠕變回復方程可分別表示為式（1）和式（2）。

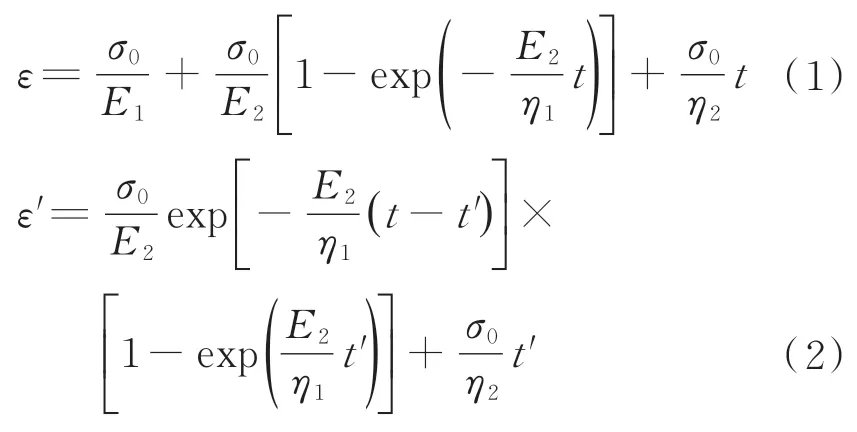
式中：ε為棉纖維蠕變應變（%）；ε′為棉纖維回復應變（%）；σ0為棉纖維應力（MPa）；t為蠕變回復時間（h）；t′為蠕變總時間（h），取值600 h。

四元件模型蠕變回復函數曲線如圖5所示。

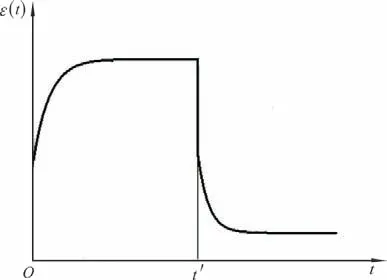
圖5 四元件模型蠕變回復曲線

可以看出，四元件模型蠕變回復曲線與棉纖維的蠕變回復曲線（圖2）基本一致，可較好表達棉纖維的蠕變行為。

3.2 應力松弛模型

五元件模型如圖6所示［12］。圖6中E0、E1、E2指彈簧的彈性模量，η1、η2指黏壺的黏滯系數。在外力作用下，材料應變ε0，彈簧E0、E1、E2瞬間響應，應力表征為ε0E0、ε0E1、ε0E2；與彈簧串聯的黏壺η1和η2逐漸響應，應力逐漸下降。當松弛時間很長時，模型達到恒定應力ε0E0。

圖6 五元件模型

五元件模型的應力松弛方程可表示為式（3）。

式中：ε0為棉纖維應變（%）；σ0為棉纖維應力（MPa）；t為應力松弛時間（h）。

五元件模型的應力松弛函數曲線如圖7所示。其與棉纖維的應力松弛曲線（圖3）相近，可較好表達棉纖維的應力松弛行為。

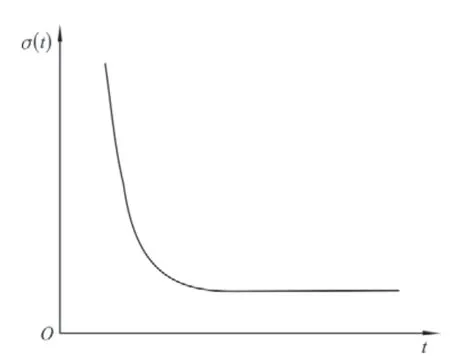
圖7 五元件模型應力松弛曲線

4 模型參數確定

為了模擬計算棉纖維的力學參數，對其蠕變、回復、應力松弛的函數關系式進行簡化。

蠕變過程，應變與時間的方程簡化為式（4）。回復過程，應變與時間的方程簡化為式（5）。

應力松弛過程，應變與時間的方程簡化為式（6）。

對圖2蠕變回復過程、圖3應力松弛過程試驗條件下的應力和時間數據分別進行非線性曲線擬合，蠕變階段擬合方程ε=32.350 1+0.014 2t-32.35exp（-t/0.003 8），相關系數R2=0.976 5；回復階段擬合方程ε=5.160 2+22.286 exp［-（t-600）/6.999］，相關系數R2=0.921 8；應力松弛階段擬合方程σ=0.072 3+8.133 73exp（-t/14.134 8）+8.133 73exp（-t/14.134 8），相關系數R2=0.999 8。可以看出相關系數R2均大于0.9，擬合效果較佳。非線性黏彈性模型能較好地表征棉纖維蠕變、回復、松弛過程，各過程分別對應的E0、E1、E2、η1、η2［13］，見表1。

表1 棉纖維蠕變、回復、應力松弛過程力學參數計算公式

5 棉纖維蠕變回復力學指標變化規律

圖8為不同載荷作用下棉纖維壓縮蠕變回復曲線，其應變指標見表2。

圖8 不同載荷的棉纖維蠕變回復曲線

由表2可知，隨著載荷增加，棉纖維的εA值增加，εBA值減少，εCB值趨于穩定，εCD值先減后增，εDE值呈增加趨勢，εE值增加。載荷增加，棉纖維的急彈性變形增加，緩彈性變形減少；棉纖維彈性回復趨減，塑性變形積累增多。載荷越大，棉纖維內部結構越易于趨向致密態，棉纖維蠕變量越小，回復能力越弱。

表2 棉纖維蠕變回復過程的應變參數

棉纖維的蠕變回復力學指標見表3和表4。可以看出，隨著載荷增加，棉纖維的蠕變回復力學指標均增大。表明棉纖維蠕變與回復力學曲線所表征的力學指標呈相似的變化規律，棉纖維蠕變與回復力學指標取決于棉纖維排布的緊密程度。載荷促使棉纖維內部結構由松散轉致密。密度越高，棉纖維內部積累彈性能量越強，黏滯效應越明顯。

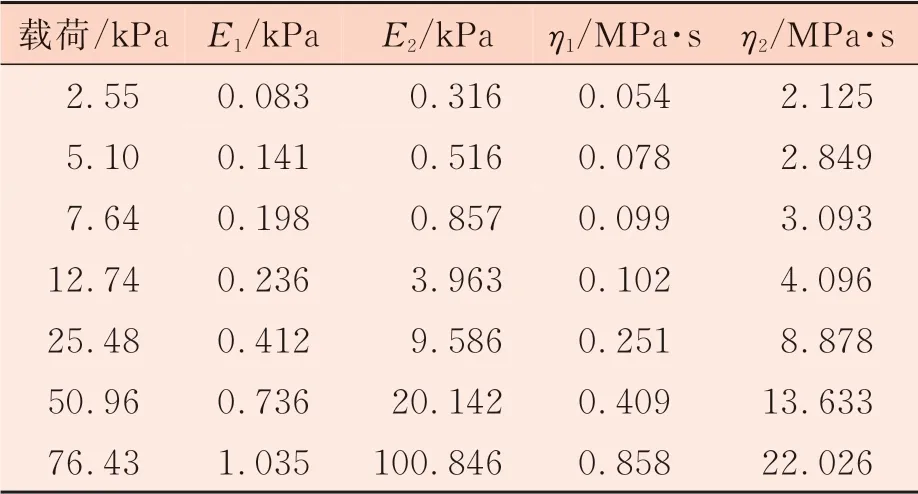
表3 棉纖維蠕變力學指標

表4 棉纖維回復力學指標

6 蠕變量與棉纖維應力的關系

蠕變期間棉纖維內部傳感器采集壓力曲線如圖9所示。

圖9 蠕變過程棉纖維內部壓力曲線

通過對比圖8蠕變曲線與圖9的壓力曲線發現，隨著蠕變量的增加，棉纖維內部應力亦增加。棉纖維的蠕變與應力數據進行線性擬合，擬合相關系數R2均大于0.9，擬合結果見表5。棉纖維的初始狀態為松散、隨機、各向異性排列，纖維與纖維之間項目搭接呈高空隙態結構。在蠕變壓力作用下，棉纖維穿插、滑移、屈曲，不斷調整形態，致使棉纖維結構致密。纖維網的致密化，強化了纖維網間力鏈分布密度概率，促使棉纖維接觸壓力傳感器感應面的幾率上升，薄膜壓力傳感器采集的壓力亦不斷增強。

表5 棉纖維內部采集應力與蠕變量關系

7 棉纖維應力松弛力學指標變化規律

圖10為不同應變條件下棉纖維應力松弛曲線。壓力傳感器采集的棉纖維內應力隨時間逐漸降低，表明壓力促使纖維形變及纖維間滑移，棉纖維內部纖維結構調節，致使棉纖維內應力略有下降。應變量越高，棉纖維內應力越高。各應變條件下棉纖維應力松弛曲線變化規律相近，應力衰減量逐漸趨近于零，屬于有限應力松弛。

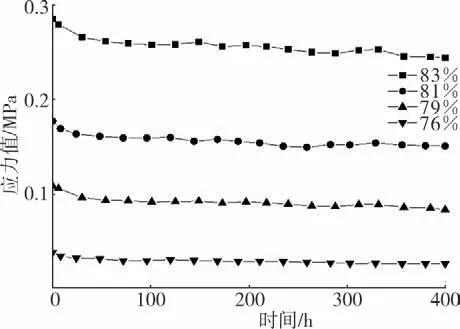
圖10 不同應變條件下棉纖維應力松弛曲線

棉纖維的應力松弛力學指標見表6。由表6可知，隨著應變增加，棉纖維的應力松弛力學指標均增大。應變增大，棉纖維內部結構趨于致密，其存儲的彈性性能、黏滯效應亦增強。

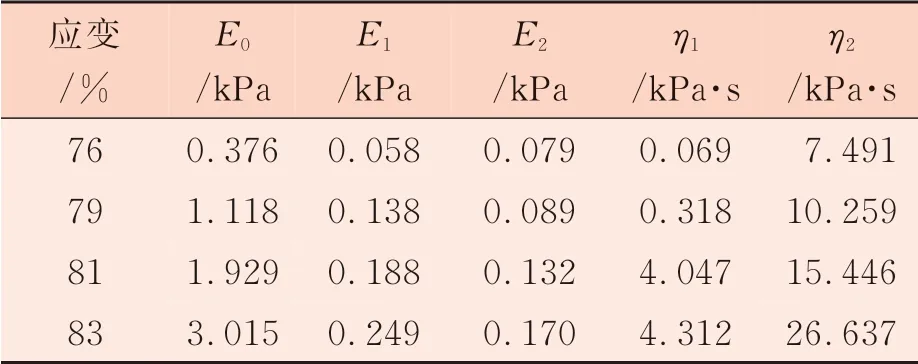
表6 棉纖維應力松弛力學指標

8 結論

（1）測試棉纖維的蠕變回復、應力松弛特性，棉纖維存在顯著的蠕變變形、形變累積和應力松弛特征。

（2）基于黏彈性理論，對棉纖維的蠕變回復、應力松弛力學特征建立黏彈性力學模型。非線性黏彈性模型能較好地表征棉纖維的蠕變回復、應力松弛力學過程。

（3）隨著載荷增加，棉纖維蠕變量與回復量均增加，棉纖維蠕變回復的力學指標E1、E2、η1、η2均增大。隨著應變量增加，棉纖維內應力增加，棉纖維應力松弛的力學指標E0、E1、E2、η1、η2均增大。密度是決定棉纖維力學指標的關鍵因素。