考慮壓力與溫度影響的螺桿馬達過盈量設計方法

鐘良春，況雨春，舒 峰，張 聰

（1.西南石油大學機電工程學院，四川 成都 610500；2.中建環能科技股份有限公司，四川 成都 610500）

螺桿鉆具廣泛應用于各個行業。馬達作為其核心部件，常在高溫、高壓和高應力循環的惡劣條件下工作［1-3］。為使螺桿鉆具能夠在惡劣條件下正常工作并保證其使用壽命，合理設計馬達定子與轉子之間的過盈量十分必要。

Ba等［4］提出了一種新的螺桿馬達設計與測試方法，但并未考慮實際工況下螺桿馬達過盈量的變化。曹剛等［5］建立了螺桿泵的三維有限元模型，并采用單向解耦方法分析了過盈量對其定子溫度場的影響。柳歡歡和鄭道寬［6-7］通過建立螺桿馬達的三維流固耦合模型，分析了馬達輸出扭矩與過盈量的關系。Alvarez等［8］預測了螺桿馬達在工作過程中的過盈量變化情況，并分析了過盈量對馬達工作性能的影響。

目前，螺桿馬達過盈量的設計大多根據經驗展開。筆者提出一種考慮工作壓力和井下溫度的螺桿馬達過盈量設計方法，并通過螺桿鉆具整機臺架試驗來驗證所提出方法的可行性，旨在為螺桿馬達過盈量以及其余參數的設計提供參考。

1 螺桿馬達有限元模型及參數

以4-5頭普通內擺線馬達為例，建立其定子與轉子的二維嚙合有限元模型，如圖1所示。其中：定子的材料為丁腈橡膠，轉子的材料為鍍鉻合金鋼，在建模時將轉子視作剛體處理。該螺桿馬達定子的大、小徑分別為：Rs=101.88 mm，rs=74.76 mm，定子的最小厚度d=15 mm。轉子的大、小徑分別為：Rr=90 mm，rr=60 mm。

圖1 螺桿馬達定子與轉子的二維嚙合有限元模型Fig.1 Two-dimensional meshing finite element model of stator and rotor of screw motor

橡膠作為一種超彈性材料，具有高度非線性和幾乎不可壓縮等特征。常用的橡膠材料本構模型包括Ogden 模型、Mooney-Rivlin（M-R）模型和Yeoh 模型［9-11］。鑒于螺桿馬達中定子的變形小于150%，選擇M-R模型。

M-R模型的一般形式為：

式中：W為應變能密度函數；Cij為材料常數；I1、I2、I3分別為材料的第一、第二和第三應力不變量；k為體積模量。

當N=1 時，上述模型即為常用的兩參數模型。假定橡膠為不可壓縮材料，則其M-R模型可表示為：

根據橡膠材料的硬度Hr與彈性模量E0的試驗值［12-13］以及計算得到的C10、C01，通過擬合可得：

通過硬度計測得丁腈橡膠試樣的邵氏硬度為75，聯立式（3）和式（4）可得C01/C10=0.015，則丁腈橡膠的本構參數為：C10=1.302，C01=0.020。

2 壓力和溫度對螺桿馬達過盈量的影響

2.1 壓力的影響

對螺桿馬達二維有限元模型的內腔表面施加20 MPa 的均勻壓力，暫不考慮溫度的影響，通過仿真計算得到其定子的位移云圖，如圖2所示。由圖2可以看出，螺桿馬達定子小徑處（即橡膠層較厚處）的變形大，大徑處（即橡膠層較薄處）變形小；定子截面的結構對稱，其位移均沿圓周方向呈周期性變化，最大位移位于定子大徑處，為0.18 mm，小徑處的位移為0.1 mm。在該工況下，若要保證螺桿鉆具正常工作，即確保其馬達的各個密封腔之間不互相串通、泄漏（螺桿鉆具正常工作時允許一定的泄漏存在），則要保證馬達的過盈量大于0.28 mm。

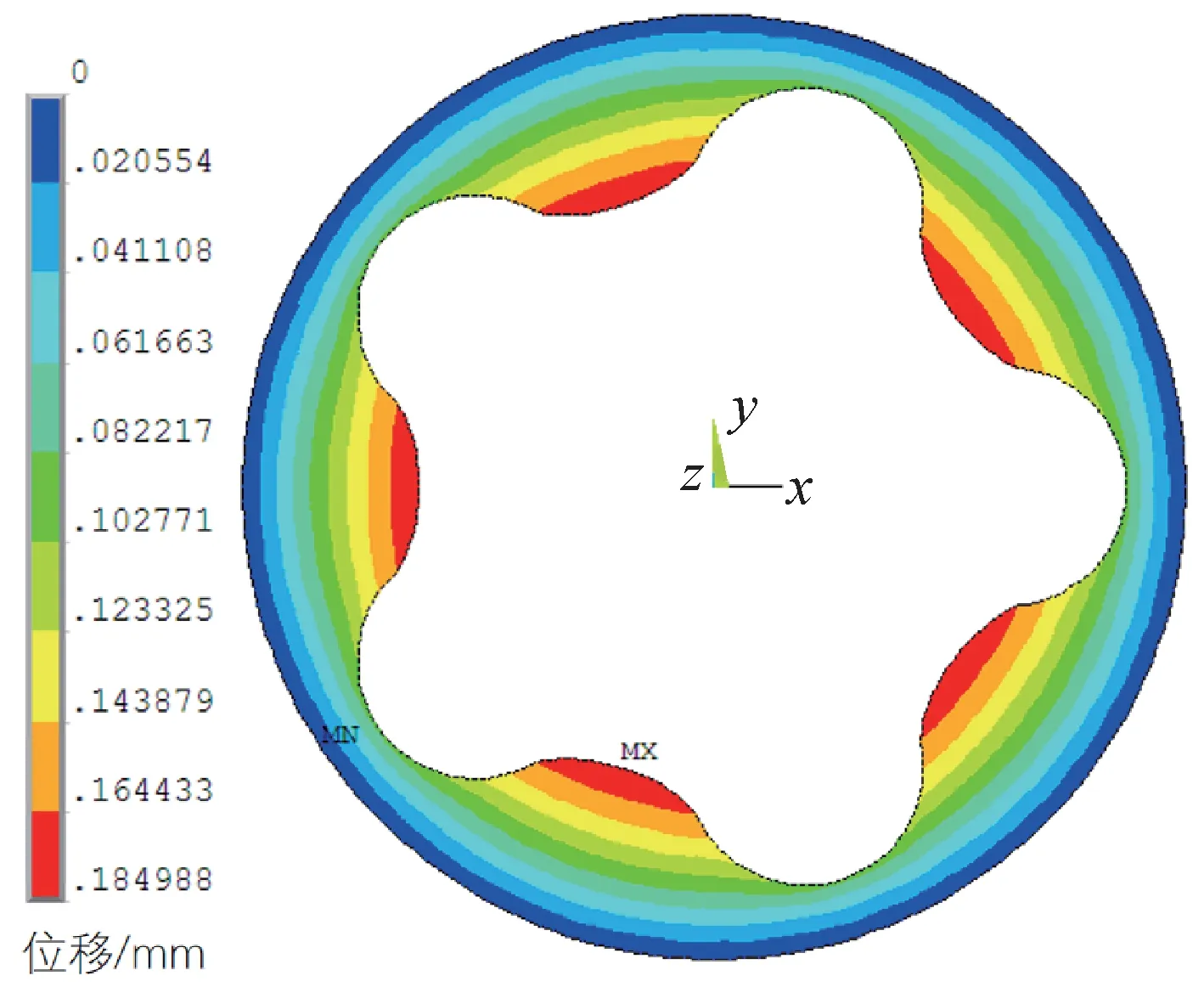
圖2 20 MPa均勻壓力下螺桿馬達定子的位移云圖Fig.2 Displacement nephogram of screw motor stator under 20 MPa equalizing pressure

在螺桿鉆具鉆進過程中，不同井段的工作壓力不同。分別取均勻壓力為20，30，40和50 MPa，對不同均勻壓力下螺桿馬達的定子進行仿真分析，得到其位移變化曲線（因定子截面的結構對稱，僅取1/10定子進行分析），如圖3所示。由圖3可以看出，不同壓力下螺桿馬達定子位移的變化規律基本相同，但隨著壓力的增大，定子大徑與小徑處的位移差越來越大，即壓力越大，定子變形程度越大。當壓力達到50 MPa時，定子大、小徑處的位移差達到了0.24 mm，由此可知傳統的均勻過盈量設計方法是不合理的。

圖3 不同均勻壓力下螺桿馬達定子的位移變化曲線Fig.3 Displacement curves of screw motor stator under different equalizing pressures

此外，由于螺桿馬達內各個密封腔的壓力不同，不同腔室之間會相互擠壓，從而導致定子產生變形。根據螺桿馬達定子與轉子的嚙合關系，選擇極限嚙合位置，此時定子與轉子之間形成了5個密封腔，如圖4所示。從螺桿馬達的入口處到出口處，工作壓力逐級降低，這也是螺桿鉆具使用一段時間后出現“喇叭口”的重要原因。因此，第1級螺桿馬達定子的變形最大且最易失效，則只須取第1級螺桿馬達的截面作為研究對象，即可確定整個馬達的過盈量。假定螺桿馬達入口處的工作壓力為20 MPa，定子與轉子的單級工作壓差為0.60 MPa，轉子按順時針方向轉動。隨著轉子的轉動，腔室面積減小的密封腔為排出腔且為增壓腔。第1級螺桿馬達截面處有5個密封腔，其中腔室1，2為排出腔，腔室4，5為吸入腔。對各腔室加載的壓力如下：對腔室1加載20.60 MPa壓力，對腔室2加載20.45 MPa壓力，對腔室3加載20.30 MPa壓力，對腔室4 加載20.15 MPa 壓力，對腔室5 加載20.00 MPa壓力。

在壓差作用下螺桿馬達定子的Mises 應力及位移云圖分別如圖5和圖6所示。從圖5中可以看出，應力集中主要出現在嚙合點A附近，位于A點高壓側的交界點處，最大Mises應力為0.372 MPa，說明該處最易磨損［14-16］。從圖6中可以看出，在嚙合點附近，高壓側橡膠明顯被擠向低壓側，定子最大變形也出現在嚙合點A的高壓側，這是因為高壓腔室1與低壓腔室5 的工作壓差為0.60 MPa，且A點處的橡膠層最厚。壓差作用下螺桿馬達定子位移的變化曲線如圖7所示。從圖7中可以看出，在最大壓差的兩側（即廓線相角為36°處），定子的最大位移達到了0.977 mm。

圖4 螺桿馬達密封腔二維模型（處于極限嚙合位置）Fig.4 Two-dimensional model of screw motor seal cavity(in the limit meshing position)

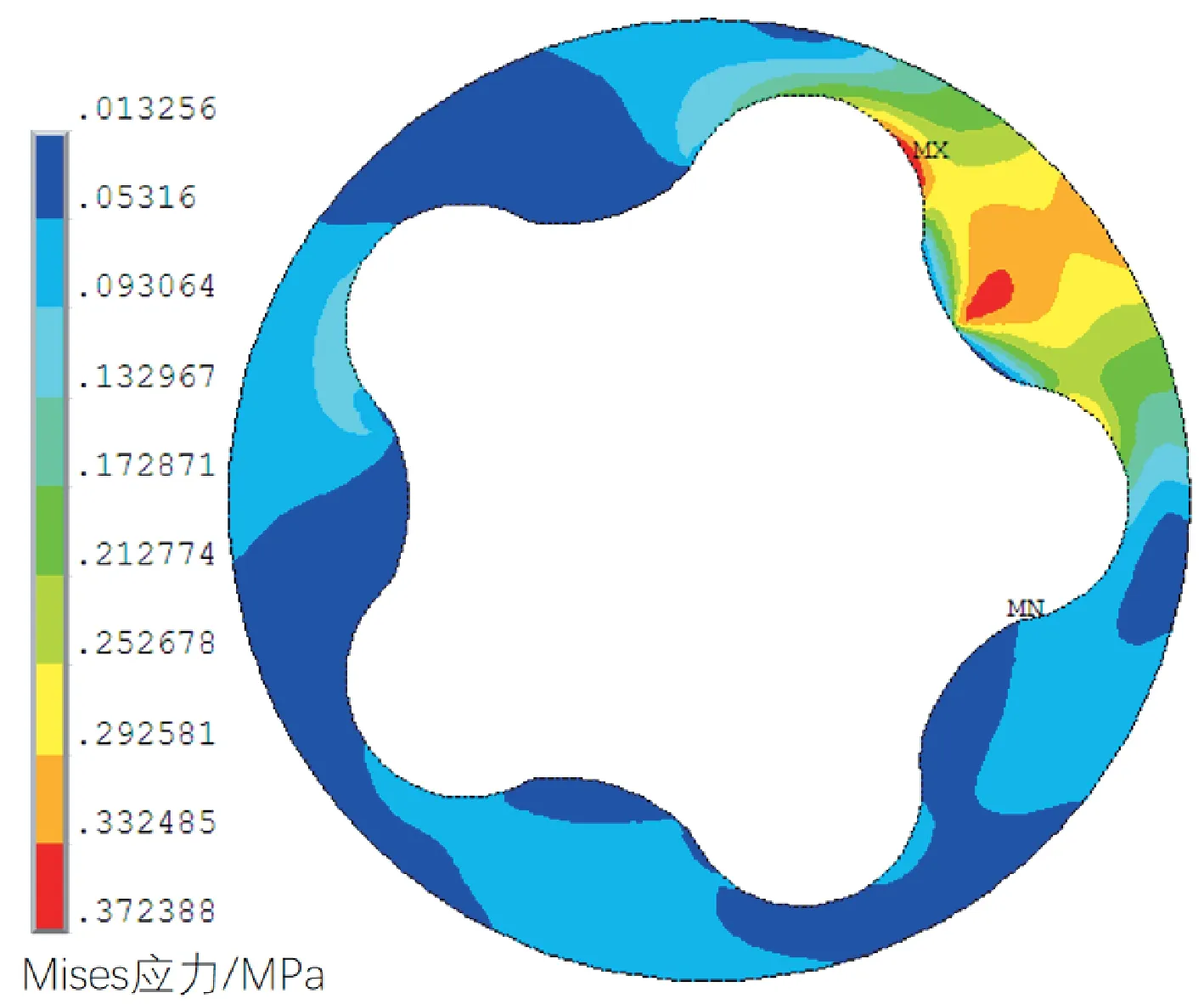
圖5 壓差作用下螺桿馬達定子的Mises應力云圖Fig.5 Mises stress nephogram of screw motor stator under the action of pressure difference

圖6 壓差作用下螺桿馬達定子的位移云圖Fig.6 Displacement nephogram of screw motor stator under the action of pressure difference

2.2 溫度的影響

在鉆井工作中，鉆井液循環使用。因黏性滯后及摩擦而產生的熱量可被不斷循環使用的鉆井液帶走。本文在采用有限元仿真分析溫度對螺桿馬達定子的影響時忽略了該因素，即視井下溫度場為均勻溫度場且不考慮壓力的影響。

圖7 壓差作用下螺桿馬達定子的位移變化曲線Fig.7 Displacement curve of screw motor stator under the action of pressure difference

在對螺桿馬達定子的溫度場進行有限元分析時，作如下基本假設：1）橡膠的材料參數和熱力學參數不隨溫度變化；2）定子與轉子在軸向上沒有熱傳導作用（即馬達軸向上無溫度梯度）。因此，螺桿馬達定子的三維熱分析問題可簡化為二維平面熱分析問題。

在考慮熱效應后，彈性體的正應變分為兩部分：1）因溫度改變，彈性體內各點自由膨脹（或自由收縮）所引起的正應變ε(T)；2）彈性體內各部分之間的相互約束所引起的正應變ε(S)。則彈性體的總正應變ε可表示為：

正應變ε(T)具有各向同性的（為相似應變），即同一點在每個方向上產生的壓縮和伸長線應變相等，且不存在切應變。若溫度變化量為ΔT，彈性體的熱膨脹系數為α，在二維平面中，則有：

正應變ε(S)與由溫度引起的應力之間服從Hooke定律，可表示為：

則熱彈性體的本構方程為：

其中：

式中：σx、σy分別為x、y方向的總正應力；εx、εy分別為x、y方向的總正應變；τxy為總切應力；γxy為總切應變。

由上述本構方程可知，溫升對熱彈性體的正應力有影響，對其切應力無影響。設螺桿馬達定子的初始溫度為20 ℃，某井段的溫度為50 ℃。基于上述本構方程，將井下溫度作為螺桿馬達有限元模型單元節點處的載荷并進行仿真分析，得到其定子的Mises 應力和位移云圖，分別如圖8 和圖9 所示。從圖8 和圖9 中可以看出，螺桿馬達定子小徑處的應力小、位移大，大徑處的應力大、位移小；當溫度為50 ℃時，定子的最大Mises 應力為0.026 MPa，最大位移為0.096 mm。

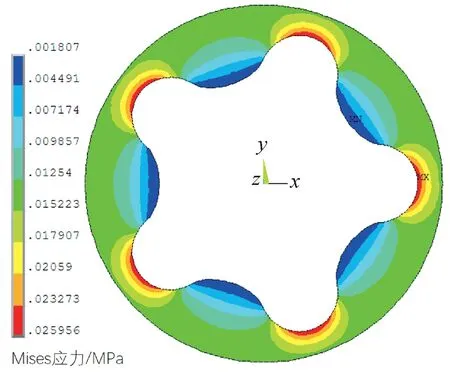
圖8 溫度為50 ℃時螺桿馬達定子的Mises應力云圖Fig.8 Mises stress nephogram of screw motor stator with temperature of 50 ℃

圖9 溫度為50 ℃時螺桿馬達定子的位移云圖Fig.9 Displacement nephogram of screw motor stator with temperature of 50 ℃

在螺桿鉆具鉆進過程中，不同井段的溫度不同。分別取井下溫度為50，60，70，80 和90 ℃，對螺桿馬達定子進行仿真分析，提取其位移變化曲線，如圖10所示。由圖10可以看出，在不同溫度下，螺桿馬達定子位移的變化規律基本相同，橡膠層越厚處的位移越大；隨著溫度的升高，定子大、小徑處的位移差增大，即溫度越高定子的變形越大；當溫度為90 ℃時，定子大、小徑處的位移差為0.26 mm。

圖10 不同溫度下螺桿馬達定子的位移變化曲線Fig.10 Displacement curves of screw motor stator under different temperatures

3 螺桿馬達過盈量及定子廓線設計

3.1 過盈量設計

過盈配合是為了使螺桿馬達定子和轉子之間形成連續獨立的密封腔，并具有一定承壓能力，從而可將鉆井液的液壓能轉化為機械能。因此，螺桿馬達的過盈量必須合理設計，否則會影響螺桿鉆具的工作性能。1）過盈量偏大會導致馬達轉子和定子之間的接觸應力和摩擦扭矩增大，從而加速定子的疲勞損壞，縮短螺桿鉆具的使用壽命；2）過盈量偏小會導致螺桿鉆具的承壓能力偏弱，從而導致其工作效率降低。

由密封性能評價準則可知［17］：當螺桿馬達定子與轉子的接觸應力大于相鄰腔室的壓差時，兩腔室間實現密封，反之則泄漏。以密封性能評價準則為基礎，對螺桿馬達的過盈量進行合理設計。假設螺桿馬達轉子作理想的行星運動，忽略其動力學因素，分別選取過盈量為0.2，0.3，0.4，0.5和0.6 mm，對不同過盈量下定子與轉子的接觸應力進行有限元仿真分析。當螺桿馬達處于極限嚙合位置時，不同過盈量下其定子與轉子的接觸應力如表1所示。

若螺桿馬達定子與轉子嚙合的危險截面（即圖4所示截面）滿足密封條件，則其他截面也滿足。由于螺桿馬達危險截面的A點為線接觸，在壓差作用下，定子產生較大的變形，導致該點處的接觸應力增大，從而達到密封條件，而其余各點均為點接觸，因壓差變形而增大的接觸應力較小，只有接觸應力達到0.60 MPa才可實現密封。由表1中可知，只有當過盈量不小于0.5 mm時，螺桿馬達才能達到密封條件。

表1 不同過盈量下螺桿馬達定子與轉子的接觸應力（處于極限嚙合位置）Table 1 Contact stress between stator and rotor of screwmotor under different interference(in the limit meshing position)

當螺桿馬達轉子的公轉角為0°時，定子與轉子的線密封長度最長，均勻接觸使得定子與轉子的接觸應力最小，如圖11所示。

圖11 過盈量為0.5 mm、轉子公轉角為0°時螺桿馬達定子與轉子的接觸應力分布Fig.11 Contact stress distribution of stator and rotor of screw motor with interference of 0.5 mm and rotor common angle of 0°

對于常規螺桿鉆具而言，在相同過盈量下其馬達定子大、小徑處的接觸應力不同，小徑處的接觸應力必然小于大徑處。基于此，提出螺桿馬達定子大、小徑處采用不同過盈量的設計方法，在保證密封性的同時盡可能使大、小徑處的接觸應力均衡。經過對不同過盈量組合下的螺桿馬達進行有限元仿真分析發現，當定子大徑處過盈量為0.2 mm，小徑處過盈量為0.5 mm，大、小徑間過盈量采用線性插值時，定子與轉子之間既能實現密封，又能良好地接觸。不同過盈量設計方法下螺桿馬達定子與轉子的最大接觸應力和Mises 應力分別如圖12 和圖13 所示。由圖12 和圖13 可以看出，相較于過盈量均勻設計（過盈量為0.5 mm）的螺桿馬達，過盈量非均勻設計的螺桿馬達的定子與轉子的最大接觸應力整體減小，減小了0.115 MPa，最大接觸應力的平均值由0.904 MPa 減小為0.813 MPa，減小了10.1%，這在一定程度上減輕了定子的接觸磨損。同時，定子的最大Mises應力在整體上也有所減小，最大Mises 應力的平均值由1.106 MPa 減小為0.980 MPa，減小了11.2%，這可使定子處的擠壓、剪切作用有所減輕，在一定程度上降低了定子的疲勞損壞速度。

圖12 不同過盈量設計方法下螺桿馬達定子與轉子的最大接觸應力變化曲線Fig.12 Maximum contact stress curves of stator and rotor of screw motor under different interference design methods

圖13 不同過盈量設計方法下螺桿馬達定子的最大Mises應力變化曲線Fig.13 Maximum Mises stress curves of screw motor stator under different interference design methods

3.2 定子廓線設計

在壓差作用下，螺桿馬達危險截面法向位移的波動較大，且不具有周期對稱性。若按該法向位移曲線對螺桿馬達過盈量進行補償設計，則在其他截面下定子與轉子嚙合時會產生較大的接觸應力。因此，取壓差作用下螺桿馬達定子的最大法向位移為臨界值，按照均勻壓力作用下定子的法向位移曲線，對螺桿馬達的過盈量進行設計。假設均勻壓力作用下螺桿馬達定子的最大法向位移為s1，壓差作用下定子的最大法向位移為s2，將均壓作用下定子的預補償量放大s2/s1倍，此時處于危險截面的定子與轉子也能實現有效密封。在某一特定井段內，必然同時存在壓力和溫度的影響，對此工況下螺桿馬達的過盈量進行設計時，假設壓力與溫度對螺桿馬達定子廓線的影響是相互獨立的，耦合壓力和溫度這2種因素引起的變形量，得到所需的定子廓線，如圖14所示，其原點為定子的形心。

圖14 考慮不同影響因素時螺桿馬達定子的廓線對比Fig.14 Comparison of stator profiles of screw motor considering different influence factors

4 試驗驗證

某公司試制的6根螺桿鉆具馬達的過盈量設計方法如表2所示。通過螺桿鉆具整機臺架試驗（試驗現場如圖15 所示），獲得螺桿馬達的性能曲線，如圖16和圖17所示。同時，根據試驗數據，采用參考文獻［18］中的公式，計算得到螺桿馬達的總效率與壓降的關系，如圖18所示。

圖15 螺桿鉆具整機臺架試驗現場Fig.15 Bench test site of screw drilling tool

由圖16至圖18可知：

1）在相同壓降下，過盈量非均勻設計的螺桿馬達的總效率較過盈量均勻設計的螺桿馬達低，這是因為過盈量非均勻設計僅為了改善定子與轉子的接觸，延長其使用壽命。

2）6個螺桿馬達的轉速均隨壓降的增大而下降，其中PDM1和PDM4的過盈量最小，密封性能較差，轉速下降最快，總效率也最低；PDM2 和PDM5 在設計時補償了壓力對過盈量的影響，其轉速最為穩定，總效率也最高；PDM3和PDM6在設計時考慮了壓力和溫度的影響，其過盈量較小，但因試驗在常溫下展開，故其轉速下降得比PDM1和PDM4快，總效率也比PDM1和PDM4低。

表2 6個螺桿馬達的過盈量設計方法Table 2 Interference design methods for six screw motors

圖16 螺桿馬達輸出扭矩隨壓降的變化曲線Fig.16 Change curves of output torque of screw motor with pressure drop

圖17 螺桿馬達轉速隨壓降的變化曲線Fig.17 Change curves of rotating speed of screw motor with pressure drop

圖18 螺桿馬達總效率隨壓降的變化曲線Fig.18 Change curves of total efficiency of screw motor with pressure drop

5 結 論

本文通過建立螺桿馬達定子與轉子的二維嚙合有限元模型，以轉子為基準，考慮壓力和溫度對馬達過盈量的影響，提出了一種過盈量非均勻設計的方法，并通過螺桿鉆具整機臺架試驗驗證了有限元結果的準確性，得到如下結論。

1）螺桿馬達過盈量均勻設計會使其定子與轉子的接觸應力過高，而采用過盈量非均勻設計方法可改善定子的受力狀況。相較于過盈量為0.5 mm的螺桿馬達，大徑處過盈量為0.2 mm、小徑處過盈量為0.5 mm 的螺桿馬達的定子與轉子的最大接觸應力的平均值由0.904 MPa 減小至0.813 MPa，減小了10.1%；定子的最大Mises 應力的平均值由1.106 MPa減小至0.982 MPa，減小了11.2%。

2）考慮壓力和溫度的過盈量非均勻設計方法可使螺桿馬達的效率得到有效提升。

綜上，所提出的過盈量非均勻設計方法及試驗數據為螺桿馬達過盈量及其余參數的設計提供了參考。