輪胎非線性縱滑力學特性的分段仿射辨識建模方法

孫曉強,胡偉偉,吳鵬程,PAK Kin Wong,陳龍

(1.江蘇大學汽車工程研究院,212013,江蘇鎮江;2.清華大學汽車安全與節能國家重點實驗室,100084,北京;3.澳門大學機電工程系,999078,澳門)

隨著人們對車輛動態性能要求的逐漸提高,許多先進動力學控制系統得到了廣泛應用[1]。包括ABS、TCS以及ACC等在內的車輛縱向動力學控制系統由于對整車行駛安全具有重要影響,近年來已成為相關領域的研究熱點[2-4]。輪胎縱滑力學特性主要用于反映輪胎縱向力與輪胎相關工作狀態間的復雜映射關系,在車輛大范圍行駛工況下呈現出明顯的非線性動態特征[5],因此構建準確的輪胎縱滑力學特性模型對于整車縱向動力學控制設計十分關鍵。傳統車輛縱向動力學控制研究由于缺乏對輪胎非線性縱滑力學特性的足夠關注,因而在一定程度上導致了系統控制性能提升受限。

構建準確的輪胎力學模型一直是車輛系統動力學領域的關注焦點之一[6-7]。現有輪胎力學模型按構建方式主要可分為經驗模型和物理模型兩大類,諸如弦模型、刷子模型、UniTire模型、“魔術公式”模型以及HSRI模型等輪胎力學模型均屬于上述范疇[8-11]。這些輪胎力學模型在精度和復雜程度等方面表現各異,但是對于推動輪胎力學模型的發展都起到了十分關鍵的作用。然而,從動力學控制的角度出發,由于在設計過程中需要反復調用輪胎模型,因此希望能夠兼顧模型精度和計算效率,但是總體上看,現有輪胎模型大多形式復雜、參數擬合困難,因而給后續在此基礎上進行系統動力學控制設計造成了不便。如何突破新型輪胎力學模型構建方式,有效協調輪胎模型精度要求與便于系統動力學控制設計二者間的相互矛盾,具有重要研究意義。

一般而言,建立系統數學模型主要有機理建模和辨識建模兩種途徑[12]。鑒于輪胎與路面接觸的復雜作用關系,通過機理建模的方式往往難以準確描述輪胎的復雜力學特性。另一方面,即使建立了復雜的機理模型,但對于后續系統控制設計可能會造成不便。隨著計算技術的快速發展以及試驗條件的不斷完善,從系統輸入輸出數據出發,借助于數據挖掘、模型辨識等技術手段,有望解決上述問題。分段仿射辨識理論旨在根據系統輸入輸出數據,通過辨識手段獲取系統數學模型的分段仿射形式[13]。根據實際經驗,絕大多數非線性系統都能通過分段仿射模型進行有效逼近。此外,值得指出的是,隨著分段仿射系統理論的快速發展,相應的優化控制理論體系逐步建立[14-15],因此基于系統分段仿射模型的動力學控制設計問題也已得到有效解決。

據此,本文考慮在準確獲取反映輪胎非線性縱滑力學特性的試驗數據基礎上,采用基于數據驅動的分段仿射辨識方法進行輪胎縱滑力學特性的辨識建模,通過將系統非線性行為在各局部工作點處進行離散分解,而后運用線性仿射方法描述系統各個局部特征,從而實現輪胎完整縱滑力學特性的有效逼近。在辨識過程中,分別采用K-means、最小二乘以及模糊加權近似支持向量機等算法完成試驗數據聚類、仿射子模型參數估計以及分解面系數矩陣求解等任務,最終獲取輪胎縱滑力學特性模型的分段仿射形式,并對模型精度進行驗證。

1 輪胎縱滑力學特性試驗

1.1 輪胎力學特性試驗臺

為準確獲取反映輪胎非線性縱滑力學特性的試驗數據,基于平板式輪胎動態特性試驗臺(如圖1所示)進行輪胎縱滑力學特性試驗。該試驗臺具有輪胎力學特性測試精度高、工況全、效率高等優點。根據相關研究,輪胎縱滑特性主要受輪胎垂向載荷、縱向滑移率以及路面附著系數等3個因素的影響。因此,本文在考慮這3個因素的基礎上,設計了輪胎縱滑力學特性試驗工況,相關參數設定見表1。

圖1 輪胎縱滑力學特性試驗臺

表1 輪胎縱滑力學特性試驗工況設定

由表1可以看出,在輪胎縱滑力學特性試驗過程中,假定輪胎不存在側偏現象,即輪胎側偏角為零。同時,由于車輛在正常行駛過程中胎壓變化幅度較小,因此假定輪胎充氣壓力保持不變。為有效反映輪胎在大范圍行駛工況下縱滑力學特性,設定了5種不同的垂向載荷,同時將輪胎縱向滑移率變化范圍設定為-1～0.5。當滑移率為負時,表示車輛制動,此時輪胎縱滑力學特性模型適用于所有制動輪,而當滑移率為正時,表示車輛驅動,此時輪胎縱滑力學特性模型僅適用于驅動輪。此外,考慮到不同附著系數路面對輪胎縱滑力學特性也有顯著影響,在試驗過程中通過變換滑臺的方式,分別模擬了兩種具有不同峰值附著系數的路面,具體峰值附著系數分別測算為0.34和0.77。

在試驗過程中,首先對輪胎施加一垂向載荷,將輪胎充至目標氣壓,而后對輪胎施加不同的驅動力矩或制動力矩,啟動滑臺帶動輪胎勻速運動,最后記錄各滑移率所對應的輪胎縱向力數值,即可獲取反映輪胎縱滑力學特性的試驗數據。

1.2 試驗結果分析

圖2和圖3所示分別為兩種不同峰值附著系數路面下的輪胎縱滑力學特性試驗結果。從圖中可以看出,輪胎縱向力與輪胎垂向載荷和輪胎縱向滑移率之間呈現出明顯的非線性關系。基于分段仿射辨識理論進行輪胎縱滑力學特性辨識的主要思想就是通過將圖中所示的不規則曲面分解為若干個平面進行擬合,而每個平面正好對應一個仿射子模型,在此基礎上,進一步結合仿射子模型切換策略,確定每個仿射子模型的工作區域,從而最終形成系統非線性模型的分段仿射形式。

圖2 低附路面的輪胎縱滑力學特性試驗結果

圖3 高附路面的輪胎縱滑力學特性試驗結果

根據上述試驗結果,通過對比不同路面附著系數下同一工作區域(垂向載荷-縱向滑移率)內的輪胎縱向力數據可以發現,輪胎縱向力的比值與路面附著系數的比值基本相同。這一現象說明路面附著系數主要影響輪胎縱向力的幅值,而對于輪胎縱向力隨垂向載荷和縱向滑移率的演化趨勢影響程度較小。該發現可以為本文在輪胎縱滑力學特性辨識過程中只針對特定路面附著系數進行辨識提供依據,從而顯著降低了系統分段仿射辨識問題的求解難度。與此同時,已有大量研究工作涉及路面附著系數的有效辨識[16-17],因此路面附著系數可視為模擬輪胎縱滑力學特性的已知條件。

綜合上述分析,本文所需完成的輪胎縱滑力學特性分段仿射辨識工作,最終被確定為辨識特定路面附著系數下輪胎縱向力與垂向載荷及縱向滑移率之間的三維非線性關系。在此基礎上,其他路面附著系數下的輪胎縱滑力學特性可按比例確定。

2 系統分段仿射辨識

對非線性系統進行分段仿射辨識就是首先將系統工作區域劃分為若干個不重疊的區域,而后獲取反映每個工作區域內系統輸入輸出間關系的仿射子模型。從理論上看,只要仿射子模型的數目足夠多,同時子模型的切換控制策略有效,那么任意的非線性系統均可通過分段仿射模型進行良好逼近。因此,本文在準確獲取反映輪胎非線性縱滑力學特性試驗數據的基礎上,采用分段仿射辨識方法進行輪胎縱滑力學特性建模。辨識工作主要是由試驗數據聚類、仿射子模型參數估計以及分解面系數矩陣求解等3個環節所組成。

2.1 分段仿射辨識問題概述

分段仿射系統的一般表達式如下[18]

(1)

式中:y(t)為分段仿射系統的輸出;φi(i=1,…,s)為每個仿射子模型的參數,s為仿射子模型的個數;ζ(t)為系統回歸向量,一般是由系統的輸入輸出向量所組成,其一般表達形式為

ζ(t)=[y(t-1),…,y(t-ny),u(t-1),…,u(t-nu)]T

(2)

其中ny和nu為分段仿射模型的階數,u為系統輸入;χi(i=1,…,s)表示系統整體工作區域,且每個子區域χi相互不重疊,具體表達式為

χi={Fiζ(t)+gi≤0}

(3)

其中Fi和gi為分解面系數矩陣。

通過式(1)～(3)實現了分段仿射系統的定義,后續在系統輸入輸出數據的基礎上,通過辨識手段獲取系統模型的分段仿射形式。

2.2 分段仿射辨識的具體流程

2.2.1 試驗數據聚類 鑒于傳統數據聚類算法可能會因異常值的存在或初始化不佳而陷入局部極小,因此本文選用改進的K-means算法進行輪胎縱滑力學特性試驗數據的聚類[19],具體步驟如下。

(1)基于原始數據集Θ={(x(j),y(j)),j=1,…,N}建立N個局部數據集Cj。每個局部數據集內是由每個數據點(x(j),y(j)),j=1,…,N和與它相鄰的c-1個點所組成,并滿足以下條件

(4)

(2)針對每個數據集,辨識其特征向量如下

(5)

(6)

其中φj(i=1,…,N)表示各局部數據集Cj的回歸向量,yCj為數據集Cj內的輸出向量。mj為反映數據集Cj內數據稀疏性的散度向量,其表達式為

(7)

(3)針對數據集特征向量進行聚類劃分。該步驟主要是將式(5)定義的各數據集特征向量劃分為s個互不相交的子集Di,為實現該目標,此處引入如下聚類目標函數

(8)

式中:μi表示各子集Di的中心;Rj為反映各局部數據集參數向量θj置信度的方差矩陣,表達式為

(9)

其中Vj為協方差矩陣,Qj為反映數據集Cj內數據稀疏性的散度矩陣,二者的具體數學表達式為

(10)

n=ny+pnu,p為系統輸入向量的維數。在上述定義的基礎上,通過尋找使得目標函數式(8)最小的子集Di和中心μi,即可實現數據集特征向量的聚類劃分。由于每個仿射子模型都應收集具有相似特征向量的所有數據點,因此通過進一步進行特征向量的聚類,即可實現仿射子模型數據集Γi的劃分。具體劃分規則如下

ξj∈Di?(x(j),y(j))∈Γi

(11)

2.2.2 仿射子模型參數估計 當完成仿射子模型數據聚類后,即可根據數據集內的數據點對仿射子模型進行參數估計。針對傳統最小二乘法因分類錯誤而產生的對異常值較為敏感的問題,本文進一步引入了反映特征向量分配合理性的置信水平因子,在此基礎上采用加權最小二乘法完成仿射子模型參數估計,具體就是計算出最合適的子模型參數向量φi(i=1,…,s),從而使得下列目標函數值最小[20]

(12)

2.2.3 分解面系數求解 在完成前述工作的基礎上,最后通過求解分解面系數矩陣即可實現輪胎縱滑力學特性的分段仿射辨識。值得指出的是,一旦原始數據點被劃分為s個數據集,則可通過計算分解面系數矩陣的方式完成數據集重構。根據線性分類原理,分解面系數矩陣的求解實則是完成s(s-1)/2個模式識別問題,而解決該問題的一個重要手段就是支持向量機。鑒于本文所涉及的數據點較多,為保證識別性能和計算效率,這里選用模糊加權近似支持向量機算法進行分解面系數求解[21-23]。相較于傳統支持向量機,該算法利用模糊隸屬度函數對每個樣本的訓練誤差進行加權,因此具有更強的抗噪聲能力,從而可以減少大量訓練樣本帶來的不利影響。基于模糊加權近似支持向量機,實現輪胎縱滑力學特性分段仿射辨識分解面系數求解的具體步驟如下。

(1)尋找兩個相鄰的子集Di和Dj,尋找過程所依據的數學公式如下

(13)

(2)建立下述分解面系數矩陣求解問題

(14)

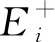
(15a)

(15b)

(15c)

(15d)

(15e)

(15f)

(16)

綜合考慮樣本的數量和分布情況,樣本平衡因子可最終確定,如式(15b)。隨后,確定樣本點i對分解面的貢獻率ti,在這個過程中本文引入了模糊隸屬度函數。首先,定義正負樣本的半徑,如式(15d),而后基于模糊隸屬度函數確定ti[24],具體計算公式如式(15f),式中λ是為防止ti為0而引入的任意小的正數。

3 辨識模型精度驗證

通過對輪胎非線性縱滑力學特性試驗數據進行上述辨識流程,最終可獲取輪胎縱滑力學特性分段仿射模型。辨識過程中每個局部數據集內數據個數以及仿射子模型個數分別設定為1 050和10。為驗證辨識模型精度,進一步將模型仿真結果與試驗數據進行對比。圖4和圖5所示分別為兩種路面附著系數下的輪胎縱滑力學特性辨識模型仿真結果。

圖4 低路面附著系數下的辨識模型仿真結果

圖5 高路面附著系數下的辨識模型仿真結果

從圖中可以看出,辨識模型的仿真結果呈現形式與原始試驗數據非常相似,說明辨識出的若干個仿射子模型能夠很好地近似輪胎縱向力與輪胎垂向載荷及胎縱向滑移率之間的非線性關系。與此同時,仿射子模型工作區域劃分也在圖4和圖5中的二維平面內通過不同顏色標注出來了。

此外,在辨識過程中,還能獲取每個仿射子模型的具體參數,如表2所示。從表中可以看出,在辨識過程中,總計辨識出10個仿射子模型。

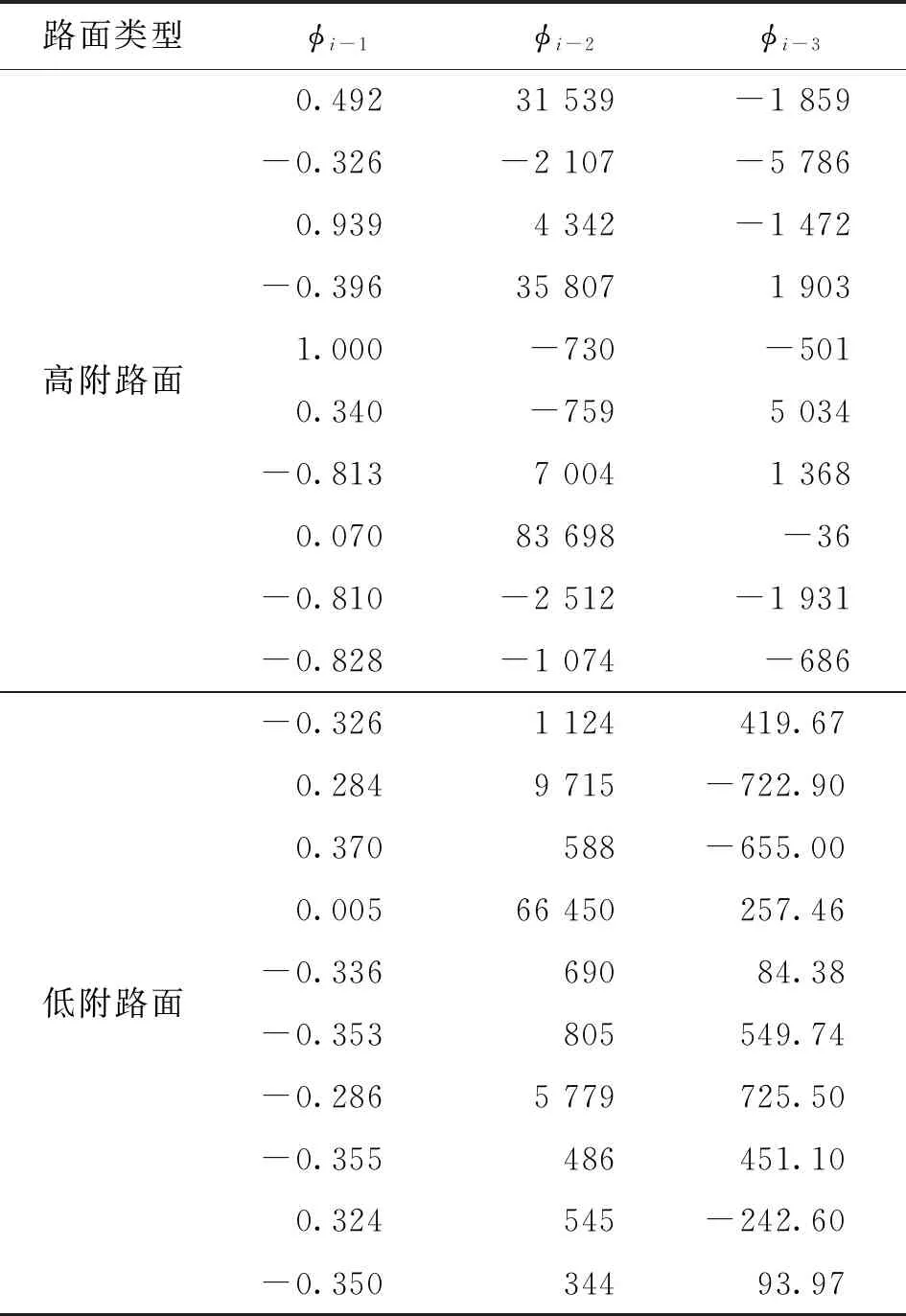
表2 辨識得到的仿射子模型參數

為進一步驗證辨識模型的精度與有效性,文中還給出了模型擬合誤差,即輪胎縱向力仿真輸出數據與試驗數據之間的差值。圖6和圖7所示分別為兩種路面附著系數下的輪胎縱滑力學特性辨識模型擬合誤差。從圖中可以看出,擬合誤差的幅值主要集中在0附近,且相較于試驗數據的幅值極小,說明所辨識的輪胎分段仿射模型具有較好的精度。

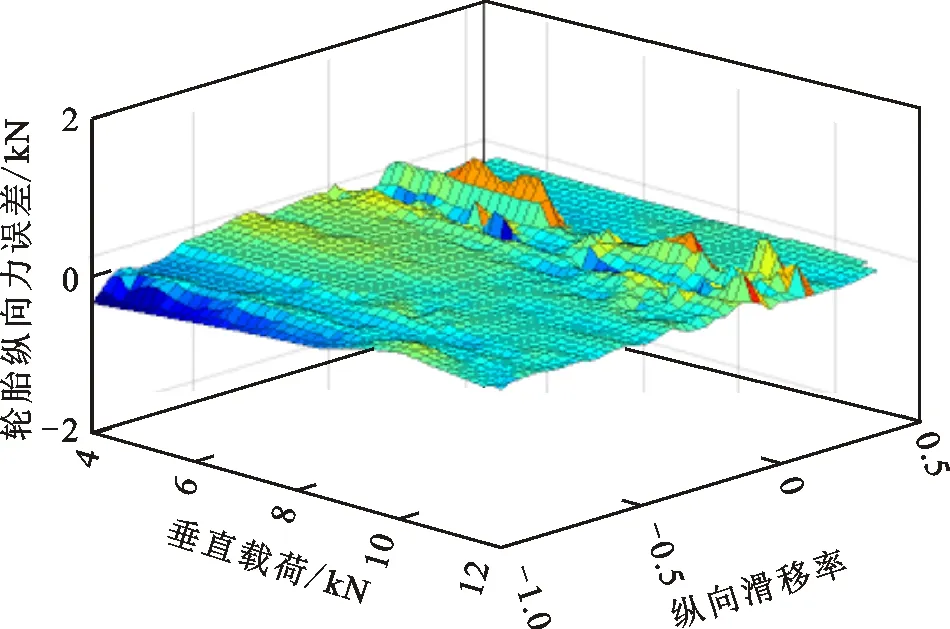
圖6 低附著路面下的辨識模型擬合誤差

圖7 高附著路面下的辨識模型擬合誤差

此外,為使得擬合誤差更清晰,在圖6和圖7所呈現的結果基礎上,圖8和圖9進一步展示了兩種路面附著系數下PWA模型與試驗數據之間的輪胎縱向力擬合誤差的二維圖。由這兩張圖可以得出相同的結論,即與實際輪胎縱向力相比,擬合誤差的幅度相對較小,這進一步表明了所得輪胎PWA模型的準確性和有效性。

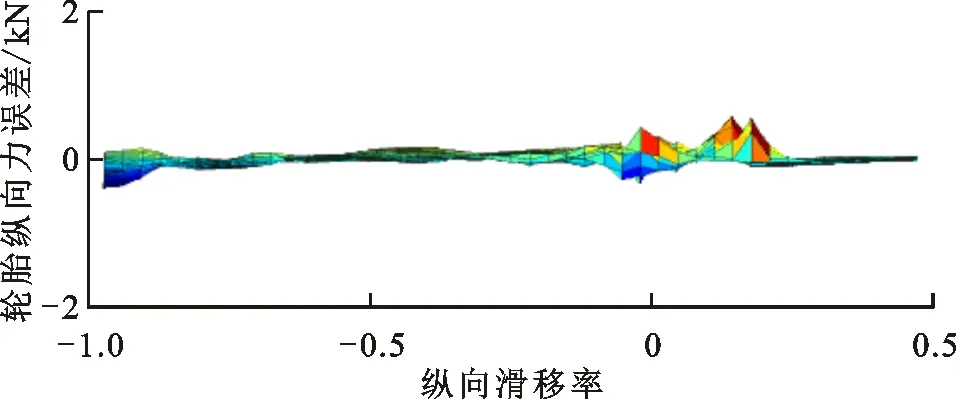
圖8 低附著路面輪胎縱向力誤差二維圖

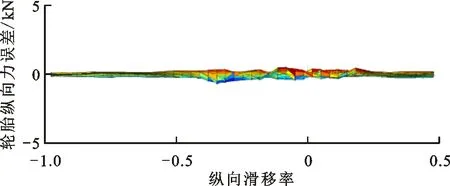
圖9 高附著路面輪胎縱向力誤差二維圖

鑒于輪胎縱滑力學特性往往是針對特定輪胎垂向載荷而給出,因此文中進一步給出了特定輪胎垂向載荷下的輪胎縱向力辨識模型仿真輸出數據與試驗數據之間的對比結果。圖10和圖11所示分別為低附路面下輪胎垂向載荷為9 468 N時辨識模型與試驗數據的輪胎縱向力對比結果以及高附路面下輪胎垂向載荷為11 760 N時辨識模型與試驗數據的輪胎縱向力對比結果。

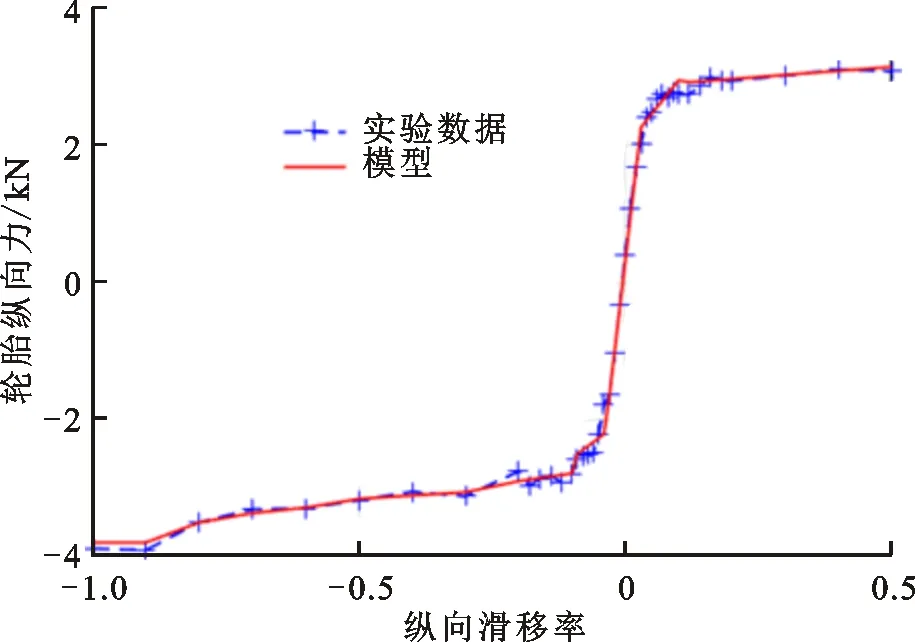
圖10 低附路面下的輪胎縱向力對比結果(9 468 N)

圖11 高附路面下的輪胎縱向力對比結果(11 760 N)

從圖中可以看出,兩種路面附著系數下由辨識模型計算出輪胎縱向力演化趨勢與試驗數據吻合度較高,且輪胎縱向力擬合誤差幾乎可以忽略不計。綜合上述對比結果表明,本文所辨識的輪胎分段仿射模型能夠準確描述大范圍行駛工況下的輪胎非線性縱滑力學特性,具有很好的擬合精度。

值得指出的是,數據量對于保證分段仿射辨識模型的精度十分關鍵。本文在試驗過程中總計采集了100 348個數據。根據辨識模型精度可以看出,在此數據量基礎上辨識得到的模型精度達到了預期要求。獲取理想辨識效果所需的數據量與被辨識對象的非線性特性往往直接相關,總體上,為保證辨識精度,應提供盡量多的數據。

4 結 論

本文在獲取輪胎試驗數據的基礎上,通過進行試驗數據聚類、仿射子模型參數估計以及分解面系數矩陣求解等工作,實現了輪胎非線性縱滑力學特性的分段仿射辨識建模,得出以下結論。

(1)路面附著系數主要影響輪胎縱向力的幅值,而對于輪胎縱向力隨垂向載荷和縱向滑移率的演化趨勢影響程度較小,輪胎縱向力主要與輪胎垂向載荷與縱向滑移率相關。

(2)通過將改進的K-means、最小二乘以及模糊加權近似支持向量機等算法進行相結合,能夠實現輪胎非線性縱滑力學特性的有效辨識。

(3)模型仿真結果與試驗數據對比表明,本文辨識得到的輪胎分段仿射模型的輪胎縱向力擬合誤差相對于輪胎縱向力幅值幾乎可以忽略不計,說明針對低附路面和高附路面,辨識得到的10個仿射子模型可以有效地擬合輪胎非線性縱滑力學特性試驗數據。基于分段仿射辨識方法獲取的輪胎辨識模型,能夠實現大范圍行駛工況下輪胎非線性縱滑力學特性的準確描述。