采用強化學習的多軸運動系統時間最優軌跡優化

張鐵,廖才磊,鄒焱飚,康中強

(華南理工大學機械與汽車工程學院,510641,廣州)

在多軸運動系統的自動化裝配、搬運等生產過程中,往往要求系統能夠高速運動以提高生產效率,但是系統的高速運動可能會導致電機動載荷過載的問題,這一現象在重載運動時尤為明顯,不僅對電機產生損害,還降低了生產質量。

為實現多軸運動系統的高速運動,需要以時間最優為目標對軌跡進行優化[1-3]。為了進一步解決高速運動過程中的電機動載荷過載問題,需要將電機動態載荷視為約束條件引入到時間最優軌跡優化數學模型中,如文獻[4]通過對系統建立動力學模型,并在軌跡優化時增加電機動態載荷約束,從而得到理論計算力矩,滿足電機動載荷約束的時間最優軌跡。但是,由于電機動子電流和定子磁場畸變以及機械參數變化等擾動,所建立的動力學模型和實際模型無法完全匹配,最終實際測量力矩仍會超出電機動載荷限制。因此,文獻[5]在動力學模型中增加補償項并利用迭代學習方法來更新補償項,以此提高動力學模型精度。雖然能夠在一定程度上減小模型不匹配度,但其仍是對理論計算力矩進行約束,無法從根本上解決高速運動中電機動載荷過載的問題。

近年來,強化學習[6]在控制領域已經有了廣泛的研究應用,例如移動路徑規劃[7-8]、步態生成[9-10]、避障[11-12]和裝配[13-14]等。這些研究用馬爾可夫決策過程來描述實際物理問題,然后利用強化學習方法進行學習求解。本文也基于馬爾可夫決策過程對時間最優軌跡優化問題進行研究,利用強化學習中智能體與環境進行交互學習的特性,提出了一種采用強化學習的時間最優軌跡優化方法:首先,將時間最優軌跡優化問題描述為馬爾可夫決策問題;其次,對經典的狀態-動作-獎勵-狀態-動作(SARSA)算法[15]進行改進,使其能適用于時間最優軌跡優化;最后,通過迭代交互法與真實環境交互學習,從而獲得滿足運動學約束和動力學約束的時間最優軌跡。本文方法無需建立動力學模型,而是直接對電機實際力矩進行約束,避免了動力學模型和實際模型不匹配的問題,從根本上解決了多軸運動系統在高速運動中電機動載荷過載的問題。

1 時間最優軌跡優化的強化學習環境

時間最優軌跡優化問題實質上是尋找滿足約束條件的電機運動軌跡,使其以盡可能大的速度工作,從而達到時間最優。為了采用強化學習方法解決時間最優軌跡優化問題,首先需要基于運動學約束條件來構造強化學習環境,動力學約束的引入需要通過與真實環境的迭代交互來完成,具體將在2.2小節研究。

1.1 時間最優軌跡優化的運動學約束

多軸運動系統包括串聯結構和并聯結構,本文主要研究串聯結構,如數控機床、串聯工業機器人等。圖1是多軸運動系統示意,可以看出,軸的運動方式主要分為轉動和移動兩種,前3軸為轉動軸,第4軸為移動軸。結構的選用及組合需要根據應用場景來設計,本文暫不考慮具體結構,只針對電機進行描述,記電機轉角關于時間t的函數為q(t)=[q1(t)q2(t)…]T。

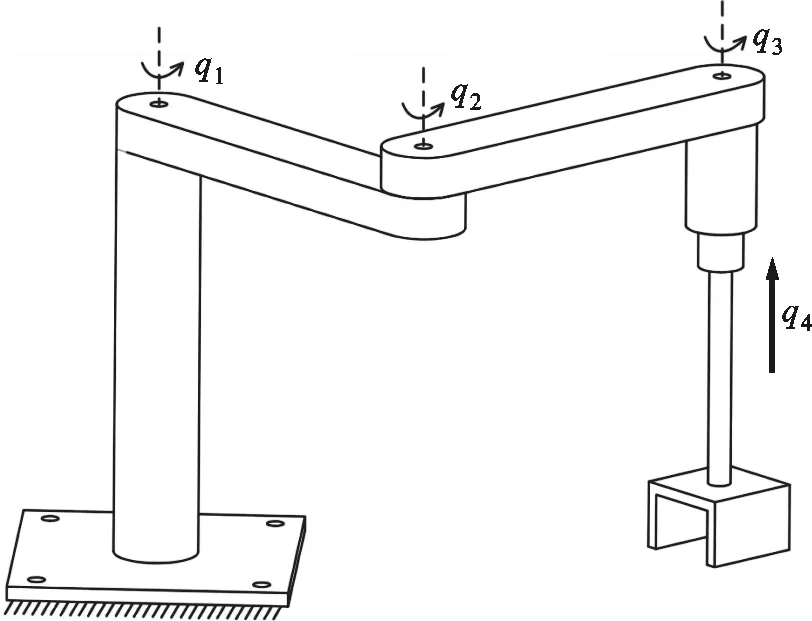
圖1 多軸運動系統示意

為了減少優化過程中的變量,軌跡優化往往在相平面上進行[16]。假設路徑標量s∈[0,1][17]與時間t存在函數映射關系s(t),則有

q(t)=q(s)

(1)

進一步地,可得到電機角速度和角加速度關于標量s的表達式

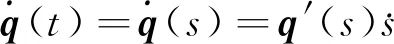
(2)

(3)

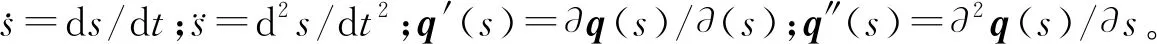
(4)

(5)

(6)

(7)

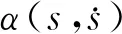
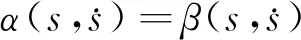
(8)

1.2 基于運動學約束的強化學習環境

對任一條運行時間為tf的完整電機軌跡,不失一般性地,假設

s(0)=0≤s(t)≤1=s(tf)

(9)

(10)

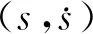
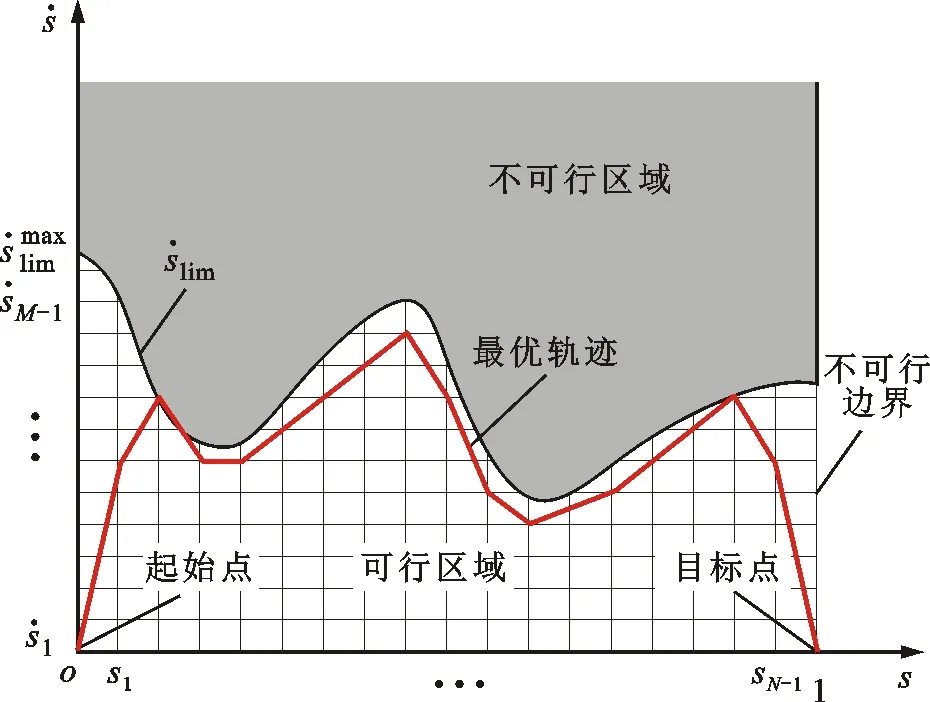
圖2 時間最優強化學習環境示意

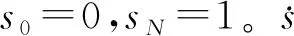
2 時間最優軌跡優化的強化學習算法

2.1 改進SARSA算法

SARSA算法[19]是一種經典的強化學習算法,其中,狀態是智能體在環境中的位置,動作是智能體從一個狀態轉移到另一個狀態所采取的行動,獎勵是環境對智能體的一個反饋。記Q(Sk,Ak)為智能體在狀態Sk采取動作Ak時獲得的平均獎勵,則用于時間最優軌跡優化的SARSA算法的學習過程如圖3所示。智能體從狀態S0開始,在狀態Sk根據Q(Sk,Ak)采取一個動作Ak,之后從環境中獲得獎勵Rk+1,更新Q(Sk,Ak)并到達下一個狀態Sk+1,這一連串狀態動作的組合稱為一個情節。

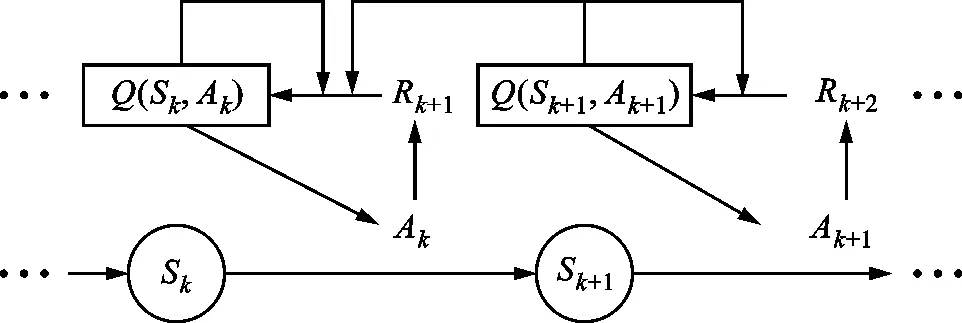
圖3 SARSA學習過程

2.1.1 動作 SARSA算法中,動作的選擇采用ε貪心法,公式為

(11)

式中λ為隨機數。

ε貪心法基于概率ε(0≤ε<1)對探索和利用進行折中:每次學習時,以ε的概率進行探索,即以均勻概率隨機選擇一個動作,以發現可以獲得更大獎勵的動作;以1-ε的概率進行利用,即選擇當前狀態下最大的Q所對應的動作,以盡可能多地獲得獎勵。此外,當處于倒數第二個狀態時,如果通過計算發現終止目標狀態點(1,0)剛好在可選擇的動作范圍內,那么這個終止目標狀態為唯一可選的動作。

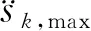
(12)

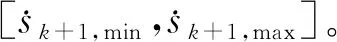
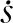
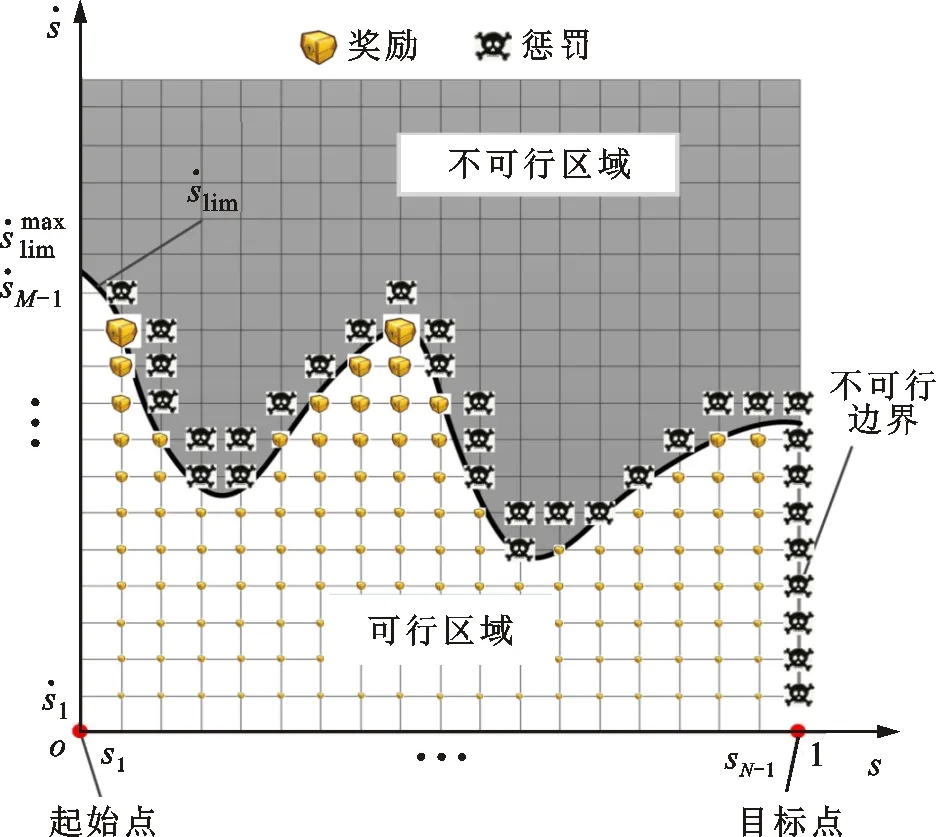
圖4 時間最優軌跡優化問題的獎勵和懲罰示意

(13)

2.1.3Q表 在經典的SARSA算法中,狀態動作函數為

Q(Sk,Ak)←Q(Sk,Ak)+α(Rk+1+

γQ(Sk+1,Ak+1)-Q(Sk,Ak))

(14)

式中:α為學習系數,0≤α<1,α越大則表示靠后的積累獎勵越重要;γ表示折扣因子,0≤γ<1。

由于SARSA算法是一個單步更新的強化學習算法,當智能體到達一個不可行狀態點并受到懲罰時,它只能通過單步更新,將懲罰往前回溯到前一步。因此,需要相當多的時間去更新Q才能使不可行狀態點的Q小于0,以保證智能體不再經過這些狀態點。為了加速這個懲罰的傳導過程,應該在智能體經歷過一段失敗的情節時,便對該段情節上的所有動作進行懲罰,使該段情節上的所有動作都能從這次失敗的情節中學到經驗。改進的狀態動作函數通過在狀態動作后面增加一個懲罰項用來加速懲罰,公式為

Q(Sk,Ak)←Q(Sk,Ak)+α(Rk+1+

γQ(Sk+1,Ak+1)-Q(Sk,Ak))+ρK-kRK+1

(15)

式中:K表示這段失敗的情節一共經歷的狀態數,0≤k≤K;RK+1表示智能體在到達第一個不可行狀態點時受到的懲罰;ρ表示懲罰折扣因子,0<ρ<1,ρ使越靠近不可行區域的動作受到的懲罰越大。

至此,得到改進SARSA算法的學習框架,如圖5所示。初始化Q表,利用改進SARSA算法進行情節學習,在經歷過一段成功的情節之后,將貪婪策略的貪婪因子ε設置為0,用于對學習到的經驗進行開采以獲得最優策略,并保存這段最優策略軌跡;重新設置一個在0～1之間的貪婪因子用于探索,并在獲得另一個成功的情節之后,重新將貪婪因子ε設置為0進行開采,獲得新的最優策略軌跡;如果新獲得的最優策略軌跡和保存的最優策略軌跡一樣,則表明智能體可能已經遍歷了所有可能的情況,并且算法收斂于最優策略。

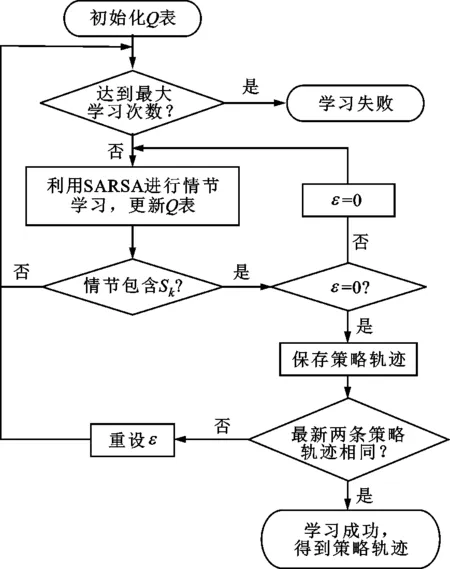
圖5 改進SARSA算法的框架

2.2 迭代交互法

根據3.1小節中的改進SARSA算法,可以學習到一條滿足運動學約束的初始策略軌跡,但是由于算法并未考慮動力學約束,因此當執行這條軌跡時,電機實際測量力矩可能超限。所以,需要通過與真實環境進行迭代交互來引入動力學約束,并對初始策略軌跡進行修正,使電機實際測量力矩最終能夠滿足動載荷約束。時間最優軌跡優化問題的迭代交互法框架如圖6所示,主要包括以下3步。

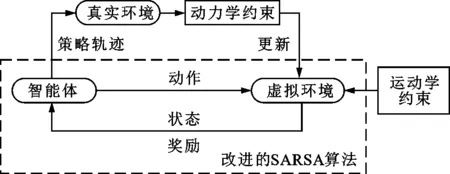
圖6 迭代交互法框架

第1步 將時間最優軌跡優化的運動學約束條件構建成強化學習環境,將時間最優軌跡優化問題構建成強化學習模型。

第2步 使用改進SARSA算法學習得到策略軌跡。

第3步 在真實環境中運行獲得策略軌跡,并采集真實的測量力矩,判斷是否超限,如果超限則將那些超限部分的狀態點都設置為不可行狀態點,從而將動力學約束更新到強化學習環境中。

重復第2、3步,直到測量力矩不再超限,便可獲得一條同時滿足運動學和動力學約束的時間最優軌跡。

3 仿真與實驗

3.1 改進SARSA算法仿真

為了驗證改進SARSA算法的有效性,在MATLAB R2018b對改進SARSA算法進行仿真驗證。考慮到實際工況中路徑的曲率多變性,本文用NURBS曲線插補器[20]生成一條曲率多變的星形曲線軌跡,并對其進行優化。星形曲線的參數中,次數k=2,節點矢量U=[0,0,0,1/9,2/9,3/9,4/9,5/9,6/9,7/9,8/9,1,1,1],頂點參數如表1所示。插補生成的軌跡如圖7所示。

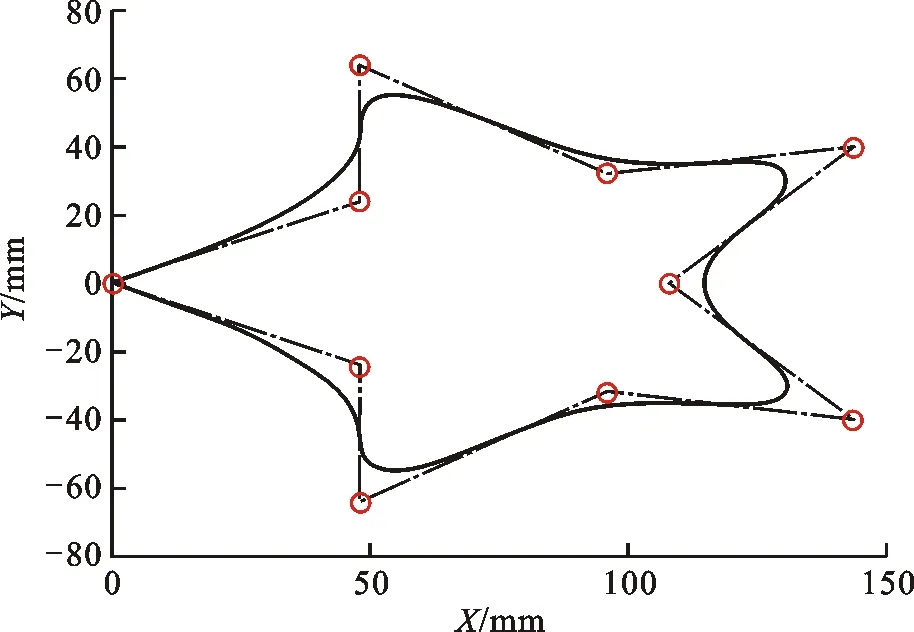
圖7 星形曲線軌跡

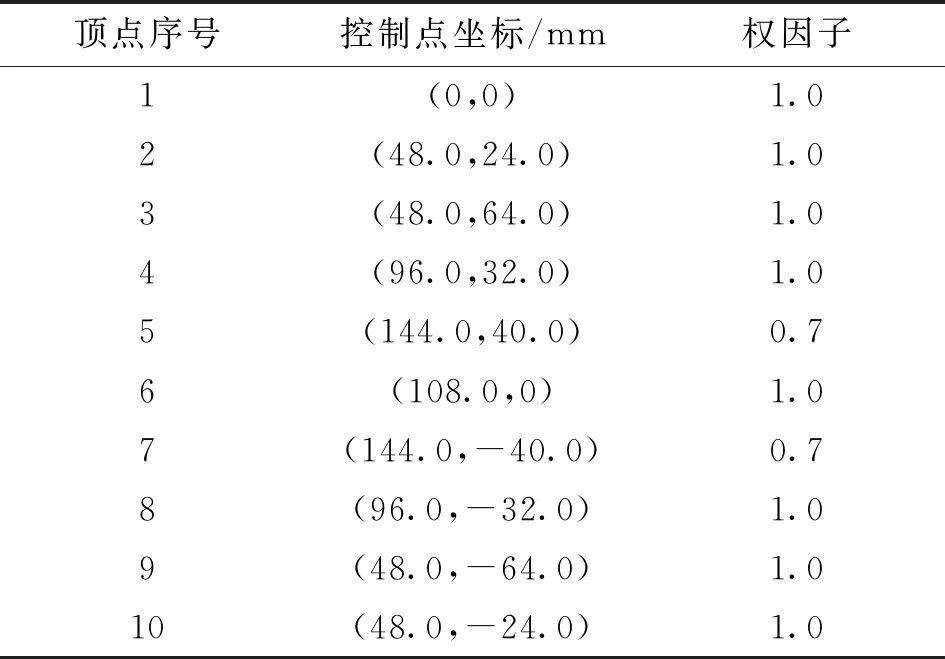
表1 星形曲線頂點參數

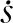
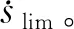
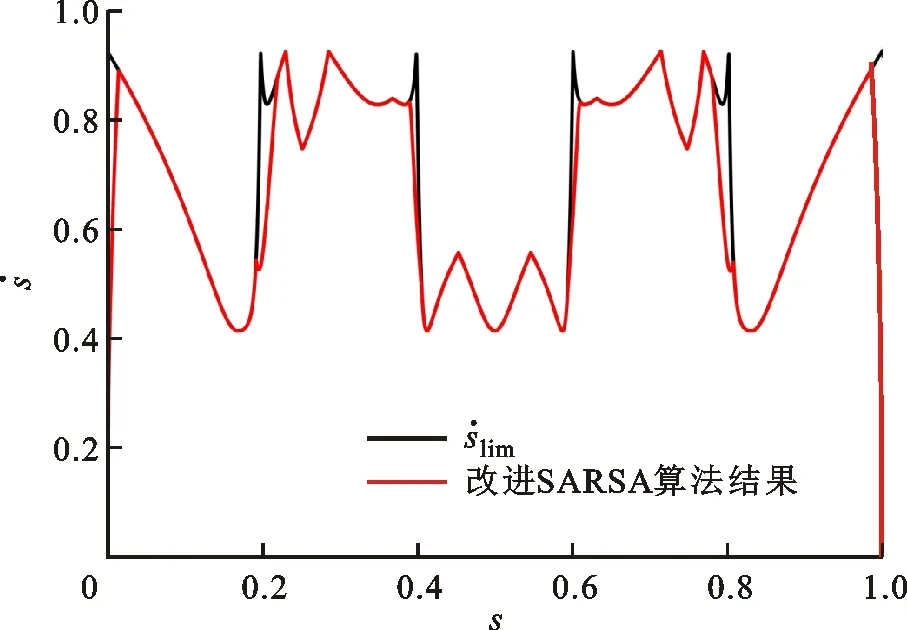
圖8 相平面軌跡優化結果

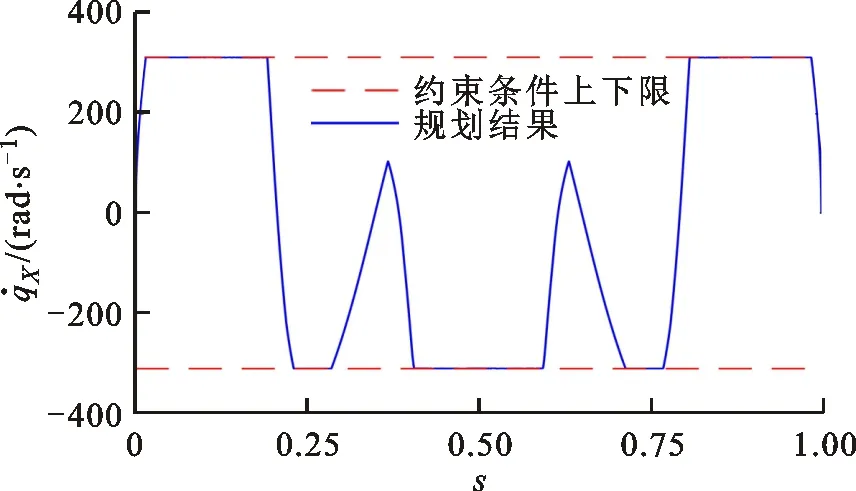
(a)X軸速度曲線

3.2 迭代交互實驗

時間最優軌跡優化的迭代交互實驗平臺如圖10所示,平臺由做獨立運動的X、Z兩軸串聯組成。兩軸的電機的型號均為Delta ECMA-CA0604RS,由Delta ASD-A2-0421-E交流伺服驅動器進行驅動,再經過滾珠絲杠將旋轉運動轉換成工作臺的直線運動。平臺的控制系統搭建于Windows7 64-bit系統,并使用EtherCAT工業以太網進行通信,控制周期和采樣周期均為1 ms。作為主站的工控機型號為DT-610P-ZQ170MA,CPU為Intel Core i7-4770,最高主頻為3.40 GHz,運行內存為8 GB。

圖10 實驗平臺

利用3.1小節中改進SARSA算法優化得到的策略軌跡與真實環境進行迭代交互實驗,結果如圖11所示。可以看出,動載荷過載點的數量隨著迭代的進行逐漸減少,且經過10次迭代之后,動載荷過載點的數量減少為0。

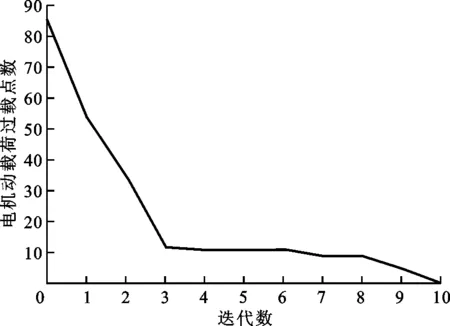
圖11 電機動載荷過載點數

迭代前和經過10次迭代后的實際測量力矩曲線如圖12所示。可以看出,迭代前X軸的部分實際測量力矩曲線超過了動載荷限制,而經過10次迭代后,X軸和Z軸的實際力矩曲線均在動載荷限制內。這是因為改進SARSA算法并未考慮動力學約束,在運行迭代前的策略軌跡時,部分點的電機動載荷過載。與真實環境進行迭代交互后,動力學約束被引入,策略軌跡逐漸得到修正,最終軌跡的實際測量力矩滿足動載荷限制。由此,迭代交互法的有效性得到了驗證。

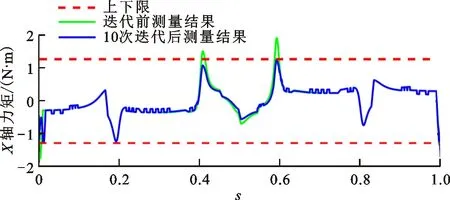
(a)X軸力矩曲線

4 結 論

為實現多軸運動系統高速運動并解決電機動載荷過載的問題,本文將時間最優軌跡優化問題描述為馬爾可夫決策問題,提出了一種采用強化學習的時間最優軌跡優化方法。該方法無需建立動力學模型,而是通過與現實環境的交互學習來直接對實際力矩進行約束,避免了動力學模型和實際模型不匹配的問題,從根本上解決了多軸運動系統在高速運動中動載荷過載的問題。

采用強化學習的時間最優軌跡優化方法根據時間最優軌跡優化問題的特性對經典SARSA算法進行改進,通過與基于運動學模型建立的強化學習環境進行交互學習,找到滿足運動學約束的初始策略軌跡。通過迭代交互法與真實環境進行交互學習,從而將動力學約束引入到強化學習環境中并對策略軌跡進行修正。最終,獲得同時滿足運動學約束和動力學約束的時間最優軌跡。

實驗結果顯示,改進SARSA算法優化得到的策略軌跡的速度和加速度曲線均在約束內,且經過10次迭代后的軌跡實際測量力矩曲線也均在動載荷約束內,提出的采用強化學習的時間最優軌跡優化方法有效。