基于GSA算法的機器人靜態路徑規劃研究

楊坤，程鵬

（1.沈陽工學院，遼寧 撫順 113122；2.沈陽理工大學，遼寧 沈陽 110159）

0 引言

機器人路徑規劃一直是學術界追蹤的熱點問題，其核心目標是身處存在阻礙的環境中，如何給機器人找出一條路徑，使其既能夠避開障礙物，又能夠到達指定目標位置。需要考慮到如何獲取環境信息、如何表示環境、如何進行路徑執行以及如何獲取知識等多方面內容。

路徑規劃可以分為在線路徑規劃和離線路徑規劃。前者是一種基于傳感器信息的環境未知的路徑規劃方法，并且必須在線規劃路徑。后者是基于環境的全局路徑規劃，適用于靜態環境的先驗完整信息，并且必須離線規劃路徑。靜態路徑規劃意味著機器人工作所在的環境是已知的且是靜態的。在機器人移動之前，路徑的選定是依照既定的環境信息進行規劃的，擇出最佳路徑后，使機器人沿著選定路徑從始發點到目的地。一般來說，可選路徑的數目不只一條。在實際應用中，通常需要在某種特定情況下選擇出一條最佳路徑。通用標準包括最短路徑，最短用時以及最低能耗[1-2]。此外，為了提升機器人在路徑規劃方面的效率并更好地滿足實時性要求，通常將遺傳算法和模擬退火算法引入機器人的靜態路徑規劃和設計中。遺傳算法雖然可以從概率的角度隨機找到全局最優解，而模擬退火算法能夠去除局部最優解，恰好彌補了遺傳算法局部尋優差的弊端。因此，遺傳算法與模擬退火算法的聯合是解決靜態路徑規劃問題的一種方法。

1 遺傳模擬退火算法

遺傳模擬退火(Genetic Simulated Annealing，GSA)算法是將遺傳算法和模擬退火算法相結合的一種優化算法。它不僅包含遺傳算法的并行性和全局性，而且包含模擬退火算法的退火性和局部搜索能力。GSA算法的基本流程：

（1）參數的選取：群體規模為n，遺傳代數最值為N，初始溫度T=T0。

（2）初始溫度變更次數l=0，0代種群Pl(k)，k=0。

（3）對現有種群執行以下步驟，直至產生下批種群。

①在初始群體Pl(k)中算出適應函數fi(t1)；依據適應函數的概率分布從Pl(k)中選n個染色體形成種群Pls(k+1)。

②按常規遺傳算法對染色體種群Pls(k+1)交叉，得到種群Plc1(k+1)；在種群Plc1(k+1)中參與交叉操作的單值i和單值j，接收概率Pi和Pj如式1和2所示。經迭代，生成新種群Plc1(k+1)。

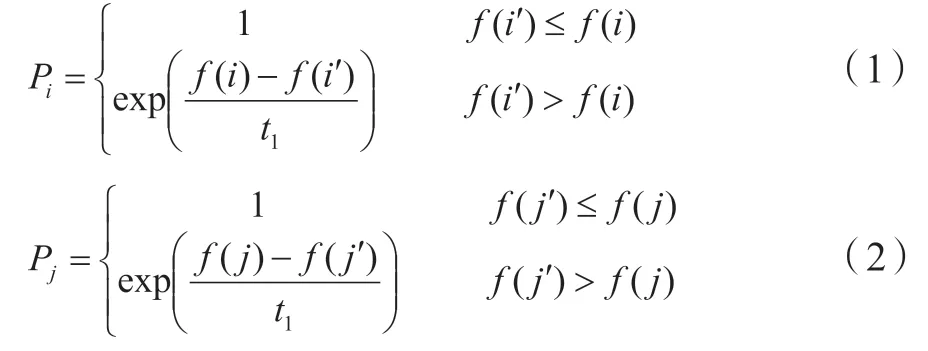
其中，種群Pls(k+1)中某單值i的目標值是f(i)，種群Plc1(k+1)中某單值i的目標值是f(i')；種群Pls(k+1)中某單值j的目標值是f(j)，種群Plc1(k+1)中某單值j的目標值是f(j')。

③根據常規遺傳算法對種群Plc(k+1)進行再變異獲得Plm1(k+1)；然后依公式（2.1）中的概率對變異后的個體進行接受，生成新種群Plm(k+1)。

④Pl(k)=Plm(k+1)，k=k+1。觀測遺傳代數，若代數為N，則轉到步驟③，若小于N，則轉向步驟①。

（4）將溫度變更，tl+1=d(t1)，Pl1(k)=Pl(k)，l=l+1，k=0。如果滿足條件，停止，輸出最優解；不滿足，則轉向步驟①。

2 機器人的靜態環境建模

環境建模是機器人通過控制傳感器感知外部環境，從而建立適合于描述外部環境的數學模型的過程。關鍵在于障礙物的表示，通常可以預測全球環境數據。環境建模利用數學模型來概括已知機器人的視角。環境建模是機器人進行路徑規劃和規避障礙的核心操作。路徑規劃方法中，被專家學者最為關注的方法之一就是網格解耦方法，它將機器人的能動空間劃分為若干簡單的網格，進而形成一個連接圖，在該圖上搜索從起始網格到目標網格的路徑。該方法可以確保只要在起點和目標點之間存在一條路徑，就可以完整地搜索該路徑[4-5]。

假定機器人處于二維工作空間內，障礙物的大小、所在坐標以及各項參數均保持不變，將此二維工作空間分成等大的網格，其面積限制在機器人可以自由移動的范圍。若是網格中不存在任何阻擋，則為自由網格；否則稱為障礙網格。網格由自由網格和障礙網格組成。機器人環境工作空間建立如圖1所示。圖中黑色區域是障礙網格。

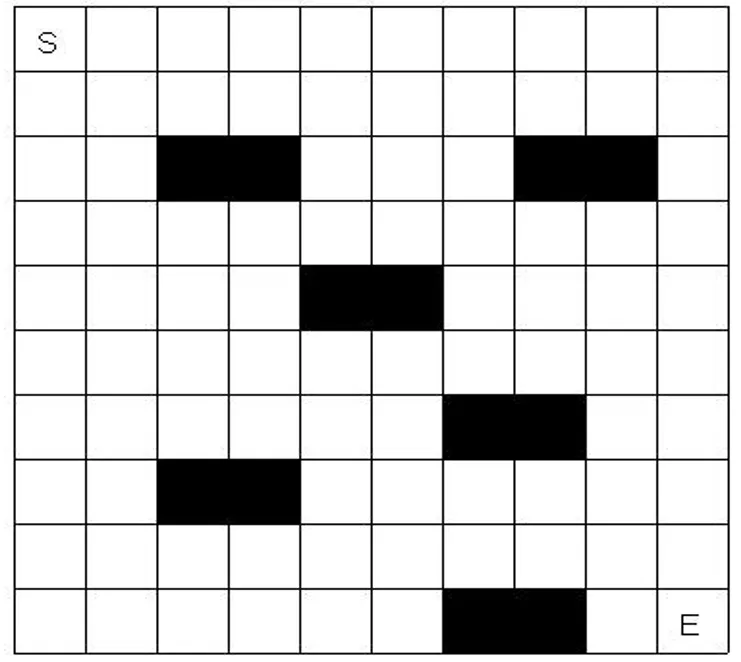
圖1 機器人環境的建立

3 路徑規劃方法設計與仿真

3.1 路徑規劃求解流程

圖2所示為基于GSA算法的路徑規劃問題求解過程。其流程可用下述步驟來描述[5-6]。

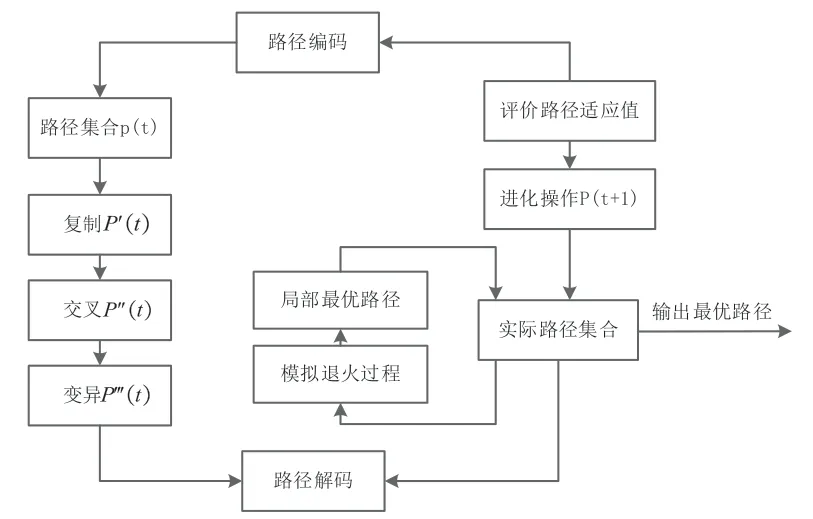
圖2 GSA算法的路徑規劃問題求解過程

步驟1：遺傳代數t初始值設為0；初始路徑集合選用隨機P(t)。

步驟2：選定初始路徑值T=max。

步驟3：評價P(t)中各條路徑的適應值

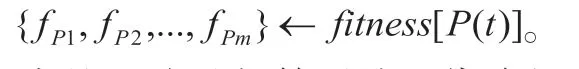
步驟5：由交叉算子進行子代路徑交叉操作

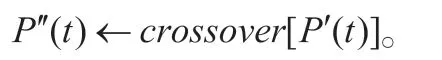
步驟6：由變異算子進行子代路徑變異操作

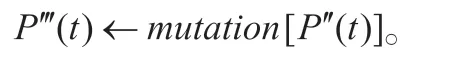
步驟7：評價P''(t)中各條路徑的適應值

步驟8：假設上述遺傳操作是由P(t)中的父代路徑PI和PJ生成：P''(t)中的子代路徑CI和CJ（I，J=1,2,...,M），選定概率Pi和Pj，將PI、PJ設為新路徑，選定概率(1-Pi)和(1-Pj)，將CI和CJ設為新路徑，進而產生單代遺傳后的新路徑

步驟9：由擇優選擇模型保留最佳路徑

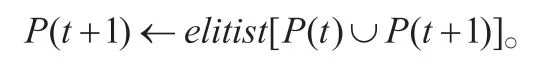
步驟10：停止判斷條件。若不滿足停止條件，則根據降溫表設定溫度T，t=t-1，返回步驟3。

當達到停止條件或增加到設定迭代次數時，即可獲得當前最佳路徑，算法結束。

3.2 仿真結果

為了驗證所提出方法的合理性和正確性，本文以Visual C++6.0為仿真工具，設M為種群個數，值為50，Pc為交叉概率，值為0.6，Pm為變異概率，值為0.01，n為編碼長度，值為16，即選用16個點構成單路。圖3和圖4分別為迭代4次和5次時的仿真結果，路徑規劃最優曲線如圖所示，該路徑無尖峰點，已知障礙物大小、方位及其參數不變。

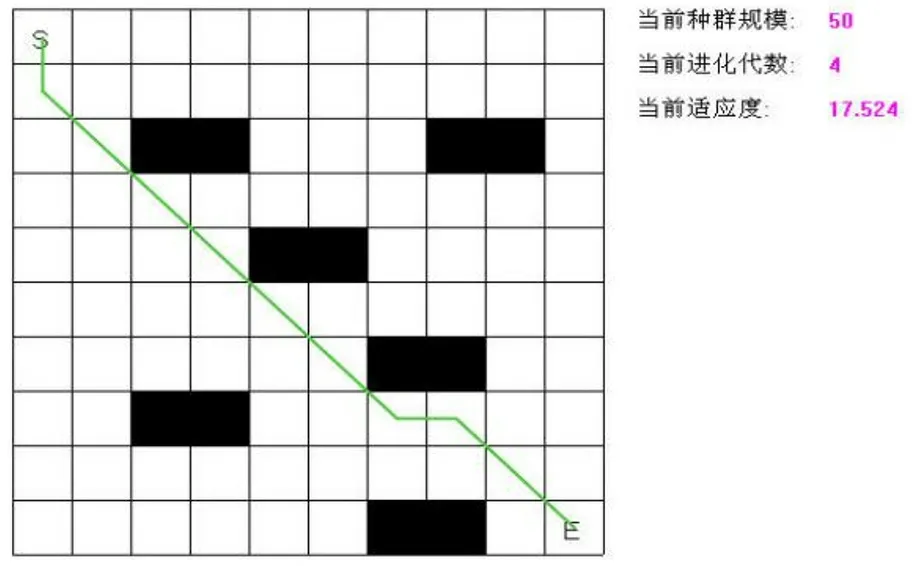
圖3 迭代4次對應的路徑規劃結果

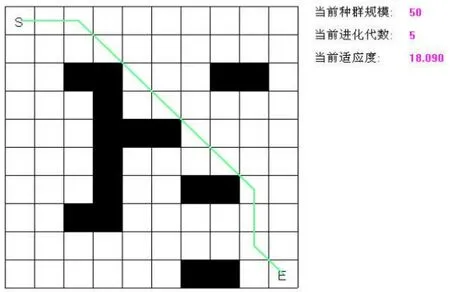
圖4 迭代5次對應的路徑規劃結果

4 結語

在對機器人傳統路徑規劃算法進行分析的基礎上，實現機器人靜態路徑規劃利用了GSA算法，驗證了該方法的合理性和正確性，為后續機器人領域的研究提供了技術支撐。