隨機載荷下基于Kriging模型的車輛十字軸結構優化*

童林軍，曾 威

(1.佛山職業技術學院汽車工程學院，廣東 佛山 528137；2.西安石油大學機械工程學院，陜西 西安 710065)

十字軸作為車輛傳動系統的重要部件，在使用過程中頻繁受到沖擊載荷的作用，若其強度不能達到使用要求，會導致軸頸斷裂，影響車輛的正常使用。為了提高十字軸結構強度，田輝等[1]采用有限元方法對某型車輛十字軸的結構強度進行了分析，并通過分析結果優化了十字軸結構，提高了十字軸的整體強度。陳科等[2]使用變曲率曲線作為軸根過渡曲線，降低了十字軸軸根位置應力集中的問題。付胡代等[3]使用ANSYS軟件分析了十字軸工況下的應力分布情況，并使用試驗設計與重復有限元分析的方式，對應力較大的軸根圓弧曲線進行了優化，提高了十字軸的強度。

上述工作通過分析十字軸工況下的應力分布情況，并對十字軸的軸根圓弧曲線半徑進行了優化，一定程度上提高了十字軸的結構強度，提高了車輛的使用可靠性。但是，在分析過程中均將十字軸載荷作為一個確定值，沒有考慮車輛在使用過程中載荷的隨機性及其對十字軸軸根圓弧半徑設計的影響，不能夠保證十字軸結構的最優性。同時，在優化過程中需要重復使用有限元方法分析不同軸根圓弧半徑下的結構強度，導致優化成本較高，優化計算求解效率較低。

本文充分考慮車輛十字軸載荷的隨機性，將之作為一個隨機變量，并使用Kriging方法構建十字軸強度關于軸根圓弧半徑的近似模型，建立十字軸結構優化數學模型，采用遺傳算法對十字軸的結構進行優化設計，獲得具有全局最優性的十字軸結構。

1 十字軸結構強度隨機有限元分析

1.1 某車輛十字軸主要結構參數

以某車輛SWC180型萬向聯軸器的十字軸為對象，其材料為20CrMnTi，軸根過渡線段使用了單一圓弧曲線，具體的結構尺寸如圖1。其中，軸根圓弧曲線半徑R=25 mm。根據文獻[1-3]的分析，影響十字軸強度的主要參數即為R，因此本文將之作為優化設計變量。

圖1 十字軸結構尺寸

1.2 隨機載荷的確定

該十字聯軸器的公稱轉矩Mj=12.5 kN·m，使用文獻[1]中的計算方法，將十字軸的載荷等效為一作用在軸頸的余弦分布載荷P(α)，具體計算公式如式(1)所示：

(1)

其中，α為任意圓心角，l為作用點到十字軸中心距離，b為分布載荷寬度，r為十字軸頸斷面圓半徑。

根據1.1節所示十字軸結果尺寸，使用公式(1)，計算得到載荷的最大值Pmax(α)=85.6 MPa。為了考慮十字軸實際載荷的隨機性，假設載荷分布服從均值μ=85.6 MPa的高斯分布，變異系數cv=0.05。基于3σ準則，確定軸頸載荷服從截斷型高斯分布，其上限、下限分別為72.76 MPa、98.44 MPa。最終，得到該十字軸的隨機載荷為：

P～N(85.6，4.282)，p∈[72.76，98.44]

(2)

1.3 隨機有限元分析

十字軸材料為20CrMnTi，在有限元軟件Abaqus中，設材料彈性模量為209×103MPa，泊松比為0.28。使用4節點Tet單元C3D4對十字軸模型進行離散，獲得十字軸的有限元模型。

為了模擬十字軸的實際工況，如圖2所示，約束圖中橫向兩軸頸的自由度，并在垂直方向兩軸頸添加如式(2)所示的隨機載荷。

圖2 十字軸邊界條件

使用Abaqus的inp文件，編寫概率分析文件，使用拉丁超立方抽樣方法對式(2)確定的隨機載荷進行抽樣，并施加在如圖2所示的十字軸軸頸上，通過靜強度計算，就能夠獲得不同軸根圓弧曲線半徑對應的最大Mises應力σ。例如，當圓弧半徑R=25 mm時，隨機載荷下十字軸的Mises應力分布如圖3所示。

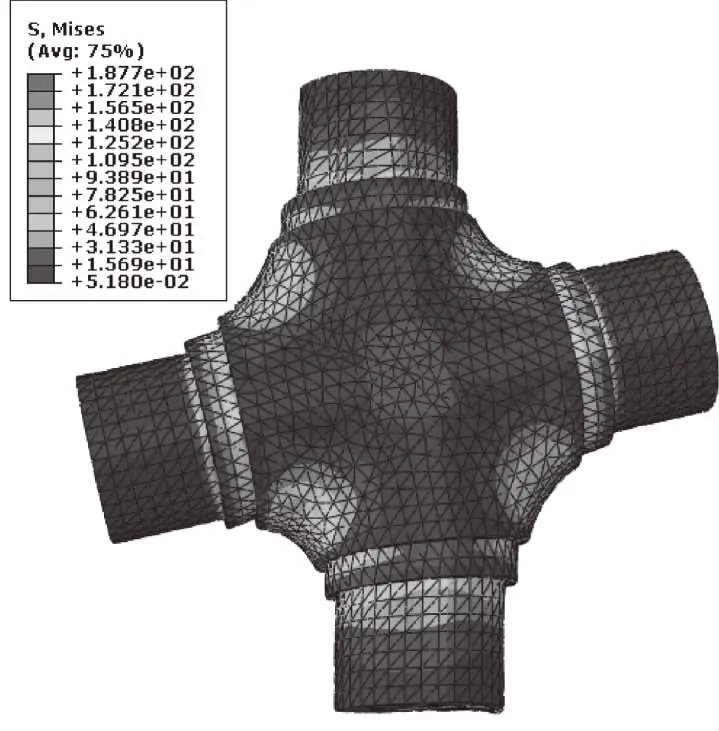
圖3 隨機載荷計算結果

2 十字軸結構強度Kriging模型

2.1 Kriging模型的基本形式

Kriging模型是一種估計方差最小的無偏估計模型[4]，能夠分析樣本數據間的相關關系，并以此預測樣本的趨勢和動態，能較好地擬合十字軸軸根圓弧半徑R與響應量σ之間的非線性關系。一個典型的Kriging模型包括回歸部分與非參數部分：

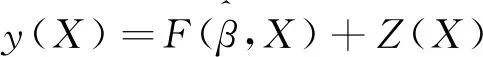
(3)

(4)

Z(X)是均值為0，方差為σ2的隨機過程，則任意兩樣本點間的相關關系可以用式(5)描述：

Cov[Z(xi)，Z(xj)]=σ2R[R(xi，xj)]

(5)

其中：σ2是隨機過程方差；R是n×n階的對稱正定對角矩陣；R(xi，xj)為任意兩個樣本點xi與xj的空間相關函數，工程應用中一般用高斯相關函數進行描述：

(6)

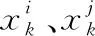
(7)

為了獲得模型的相關參數θk，可用式(8)所示的最大似然估計方法：

(8)

獲得Kriging模型的相關參數θk之后，即可通過式(7)得到預測值，最終構建得到十字軸應力σ的Kriging模型。

2.2 十字軸結構強度Kriging模型的構建

為構建十字軸結構強度Kriging模型，以十字軸軸根圓弧半徑R為優化設計變量，以隨機載荷作用下十字軸最大Mises應力σ為響應值。Kriging模型的訓練樣本數量m=3k，其中k=(n+1)(n+2)/2，n為設計變量個數。因為本文設計變量數n=1，因此訓練樣本點數為9。

以當前圓弧半徑R=25 mm為中心，上下浮動50%，確定訓練樣本的取值區間為R∈[12.5，37.5]。為了保證樣本的均勻性，使用拉丁超立方試驗設計方法[5]，從變量取值區間中抽樣9組設計變量值，使用第2節構建的隨機有限元方法，計算不同圓弧半徑對應的Mises應力值，并將之作為十字軸Mises應力Kriging模型的訓練樣本，如表1。

表1 Kriging模型訓練樣本

(9)

用式(8)計算得到模型的相關參數θk，得到Mises應力的Kriging模型相關參數θk=0.121。最后，能夠計算任意點x與已知樣本數據間的相關向量rT，通過式(7)得到響應值，即構建得到Mises接觸應力的Kriging模型。

為了檢驗構建的Kriging模型的預測精度，采用均方根誤差[6]作為精度檢驗指標。由式(7)可得Kriging模型預測點的均方根誤差為：

(10)

檢驗時，在表1中隨機選取了5組訓練樣本數據作為誤差檢測樣本，將之與由Kriging模型擬合得到的Mises應力值進行對比，獲得的RMSE值為0.032，表明構建的Kriging模型具有較高的預測精度，能夠擬合十字軸Mises應力隨機有限元分析結果。

3 基于Kriging模型的十字軸軸根圓弧半徑優化

3.1 十字軸軸根圓弧半徑優化設計模型

以十字軸軸根圓弧半徑R為優化設計變量，以隨機載荷作用下十字軸的最大Mises應力σ為響應值，使用構建的Mises應力Kriging模型為目標函數，構建軸根圓弧半徑R的優化設計模型：

(11)

式中，σ(R)是構建Mises應力Kriging模型。

3.2 基于多島遺傳算法的軸根圓弧半徑尋優

為了獲得全局最優的十字軸軸根圓弧半徑R，須使用優化算法對式(11)所示的軸根圓弧半徑優化模型進行求解。多島遺傳算法[7]能高效率的獲得具有全局最優性的優化解，本文使用該算法對軸根圓弧半徑進行尋優計算。尋優計算過程如圖4所示。

根據圖4所示的優化結果，十字軸軸根圓弧半徑R的最優值為27.27 mm。為了檢驗該結果的準確性，將優化后的圓弧半徑R代入到隨機有限元模型中進行結構強度分析，在相同工況下，得到此時十字軸的Mises接觸應力值為150.1 MPa，如圖5所示。與原始結構對應的Mises應力值相比，Mises應力值降低了37.6 MPa，驗證了本文優化方法的有效性。

圖4 設計參數尋優歷程

圖5 優化后的Mises應力分布

4 結論

1)以十字軸軸根圓弧半徑為設計變量，以車輛十字軸工況條件下的Mises應力為十字軸結構強度衡量指標，構建了十字軸結構強度的Kriging模型，為十字軸結構強度計算提供了高精度的近似模型。

2)構建了以十字軸結構強度Kriging模型為目標函數的軸根圓弧半徑的優化模型，并使用多島遺傳算法獲得該十字軸軸根圓弧半徑的最優值。優化后，工況條件下十字軸Mises應力降低了37.6 MPa，該優化方法得到驗證。