一種基于波形包絡趨勢變化的AE信號到時拾取方法①

謝學斌，葉永飛，高 山，劉 濤，王小平

（中南大學 資源與安全工程學院，湖南 長沙 410083）

到時拾取是進行聲發射參數分析、聲源定位、矩張量反演的重要前提［1－3］，在實際監測中到時拾取多采用人工識別和閾值法［4］，但極易受個人經驗的影響，已不適用于大量監測數據中的到時識別。為此，學者們將地震領域相關算法引進到了AE信號到時拾取中，根據各算法的特點可歸納為兩類：一是根據監測信號的變化特征識別到時，比較經典的有STA／LTA法［5］、AIC法［6］、高階統計法［7］、MER法［8］、機器學習法［9］；二是綜合判別分析，該類算法先通過某種算法粗略拾取到時，再結合其他算法確定精確到時，如STA／LTA與AIC法聯合確定到時［10］。

前述眾多算法存在2個共同的缺點，一是各種算法過度依賴參數選擇，當參數選取不合適時往往會造成漏拾、誤拾；二是為保證精度，需事先進行一定降噪處理，這不可避免地造成有用信息損失，進而影響到時拾取的可靠性。總之，上述算法雖能在一定程度上實現到時自動識別，但在礦山龐大的監測數據量和復雜的噪音環境下存在明顯局限性。

為了避免上述方法的局限性，本文利用時間序列處理的相關算法，通過對監測信號的幅值包絡進行去周期去殘差，獲得監測信號的幅值趨勢變化特征，再通過趨勢突變檢測確定到時，避免了繁雜的參數設定和降噪處理，具有較強的適應性。

1 基于波形包絡趨勢變化的到時拾取方法

如圖1所示，AE信號幅值變化能明顯區別于純噪音部分，這是眾多到時識別算法的依據，而信號幅值變化程度可通過其包絡線來反映［11］，但包絡線存在周期變化特征和異常殘差，極易對到時判斷產生干擾。從圖1可以發現AE信號出現前包絡線的趨勢是穩定的，AE信號出現后包絡線的趨勢明顯突變，因此可通過趨勢突變點來確定AE信號到時。

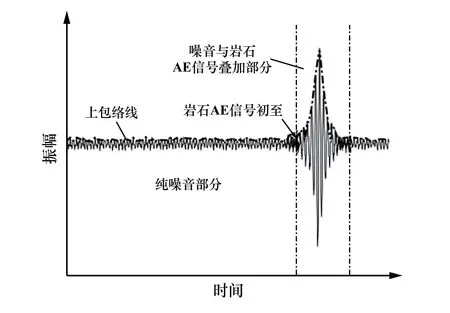
圖1 監測信號示意

1.1 波形包絡

如圖1所示，波形包絡可由其外部拐點來構成［11］，拐點可分為上下拐點，對應的包絡線也可分為上下包絡線，上下包絡線可通過監測信號均值來區分，即大于監測信號均值的拐點構成波形上包絡線，小于監測信號均值的拐點構成波形下包絡線，本文只選取上包絡線進行研究。

1.2 包絡線隱周期估計

去除上包絡線X b的周期變化，需事先確定包絡線的隱周期，隱周期是包絡線最有可能存在的周期，包絡線的隱周期S與監測信號的隱周期相同，監測信號的隱周期可通過功率譜密度圖進行大致估計［12］，即功率譜密度中最大極值點對應的頻率f0求導后即為所求包絡線的隱周期。

1.3 基于STL分解確定包絡線的趨勢曲線

確定上包絡線Xb的隱周期后，包絡線的變化趨勢可通過STL分解獲得。STL分解是通過LOESS回歸將包絡線X b分解為趨勢分量T t、周期分量S t和殘差R t：

STL分為內循環與外循環，內循環嵌套在外循環中，假定內循環中第v－1次結束時各分量為Tt（v）、S t（v），內循環可分為以下6個步驟：

1）去趨勢，減去上一輪結果的趨勢分量Xt－T t（v）；

2）LOESS回歸進行周期子序列平滑；

3）平滑周期子序列的低通濾波；

4）去周期子序列趨勢，S t（v＋1）＝Ct（v＋1）－L t（v＋1）；

5）去除周期項X t－S t（v＋1）；

6）LOESS回歸進行趨勢平滑得到T t（v＋1）。

外層循環主要通過產生魯棒權重來抑制包絡線中的異常值，對于時間為t的數據點，其魯棒權重為：

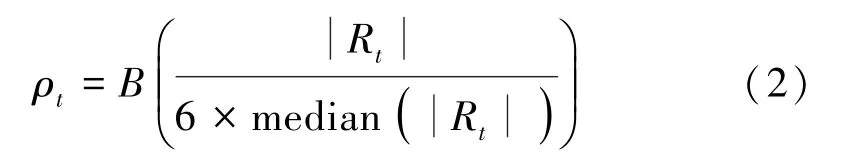
式中B函數為Bisquare函數：

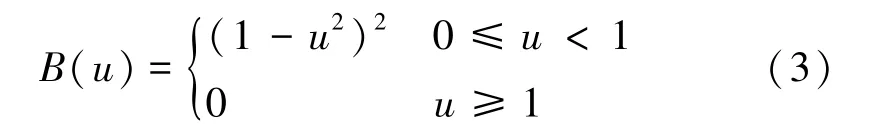
1.4 基于MK突變點檢測確定到時

MK檢測是一種穩健的非參數突變檢驗方法，可對包絡線的趨勢曲線突變進行檢測，具體內容如下：

對于長度為l的趨勢曲線序列Tt，構造秩序列：

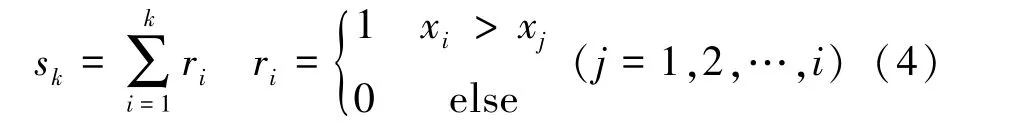
式中s k為i時刻數值大于j時刻數值個數的累計。在時間序列隨機獨立的假設下，定義統計量：

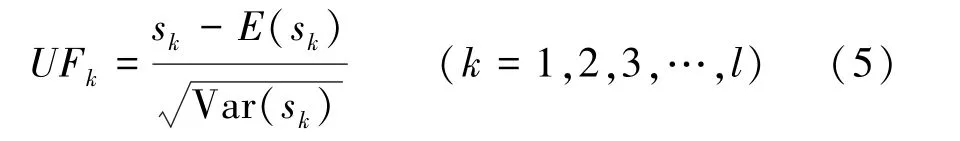
式中UF1＝0；E（s k），Var（s k）為累計數s k的均值和方差。

按趨勢序列T t逆序x l，x l－1，…，x1計算逆序秩序列s k′，再重復上述過程，同時使UB k＝－UF k（k＝l，l－1，…，1），UB1＝0。MK突變點檢測步驟如下：

1）計算順序秩序列s k，并按式（5）計算UF k。

2）計算逆序秩序列s k′，并按式（5）計算UB k。

3）給定顯著水平α，尋找臨界值±Uα，如果在兩臨界值±Uα之間UF k與UB k存在交點，該點對應的時刻t g即為巖石AE信號到時；如果不存在交點即無聲發射出現。

2 仿真實驗

為驗證本文到時拾取算法在不同噪音環境下的實際性能，通過MATLAB生成如下動態仿真信號來模擬礦山監測信號：

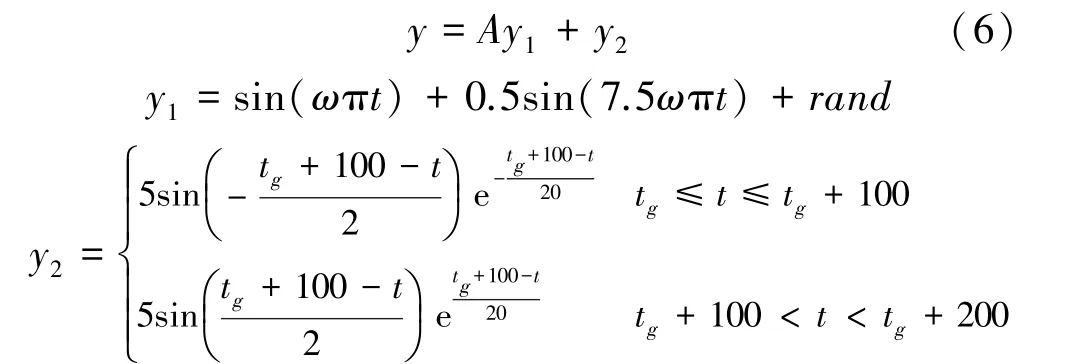
式中Ay1為模擬背景噪音，其強度、主頻率可通過A、ω來控制；y2為模擬AE信號；相應的t g為其到時，仿真中取700 s；rand為隨機函數，仿真中采樣間隔為1 s，采樣長度為1 024 s。

如表1所示，在仿真實驗中通過調節幅值參數A、頻率參數ω，生成了極強、強、一般、弱共4種噪音環境（信噪比分別為3 dB、5 dB、10 dB、20 dB）下的12類共60組模擬信號。為評判本文方法的拾取性能，與運用較多的STA／LTA法進行了對比，結果如表1所示，表中誤判率為拾取誤差大于100 s事件所占比例，漏判率為未識別到時事件所占比例。為體現STA／LTA對相關參數依賴性，設置了2 s、4 s、8 s共3種不同短時窗對有效信號到時進行拾取，此外長時窗設為32 s，自動提取閾值設為2.5。從表1可以發現，在各類噪音環境下本文方法均能拾取到時，而STA／LTA法對短時窗的選擇具有明顯的依賴性，且準確率較低。當短時窗取2 s時，STA／LTA法均出現了誤判；當短時窗取4 s時，STA／LTA法拾取性能明顯得到改善，但隨著噪音增強其誤判、漏判明顯增加；當短時窗取8 s時，STA／LTA法拾取偏差明顯過大，且ω＝0.4時STA／LTA法已無法拾取到時。從表1可以看出，在仿真中本文方法準確度明顯優于STA／LTA法，且對于低信噪比（SNR＝3）和高頻率（ω＝0.4）噪音均有相對較好的拾取性能。

圖2為ω＝0.2時，不同噪音環境下的4組模擬信號的波形。將圖2（a）、（b）與圖2（c）、（d）對比后可以發現，隨著背景噪音增強，部分有效信號很難從幅值上進行區分辨別，從波形幅值上判斷到時容易出現較大誤差，相應的在強噪音環境下人工法和閾值法拾取到時很難保證有足夠的準確率。對圖2中的包絡線進行STL分解后，得到圖3所示的變化趨勢曲線。從圖3可以直觀地發現，到時前后包絡線變化趨勢明顯不同，而趨勢的分界點可以通過MK突變檢測來判斷。對圖3中的包絡線進行MK檢測，得到如圖4所示的變化趨勢曲線。從圖4可以發現，在不同強度的噪音環境下，在0.05顯著水平內UF曲線與UB曲線均有交點，即均能拾取到時，從到時拾取結果（圖4中交點橫坐標）可以看出，隨著噪音強度增強，本文方法拾取偏差也會增大，但相比于STA／LTA法（見圖5）卻有更好的性能，SNR為10 dB和20 dB時本文方法偏差分別為11 s和6 s，而STA／LTA法偏差分別為80 s和39 s，明顯大于本文方法，當SNR為3 dB和6 dB時STA／LTA法出現了誤判。從圖5可以發現，STA／LTA法對閾值的設置也存在明顯的依賴性，不同噪音環境需要設置不同的閾值，STA／LTA法才能發揮作用。

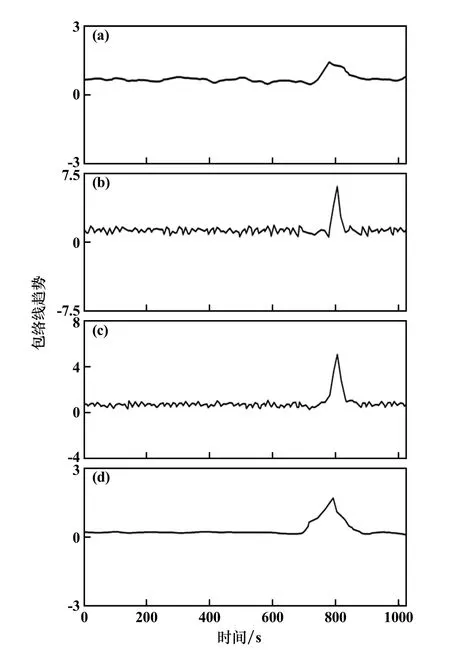
圖3 STL分解后包絡線趨勢變化曲線

圖4 MK檢測后包絡線趨勢變化曲線

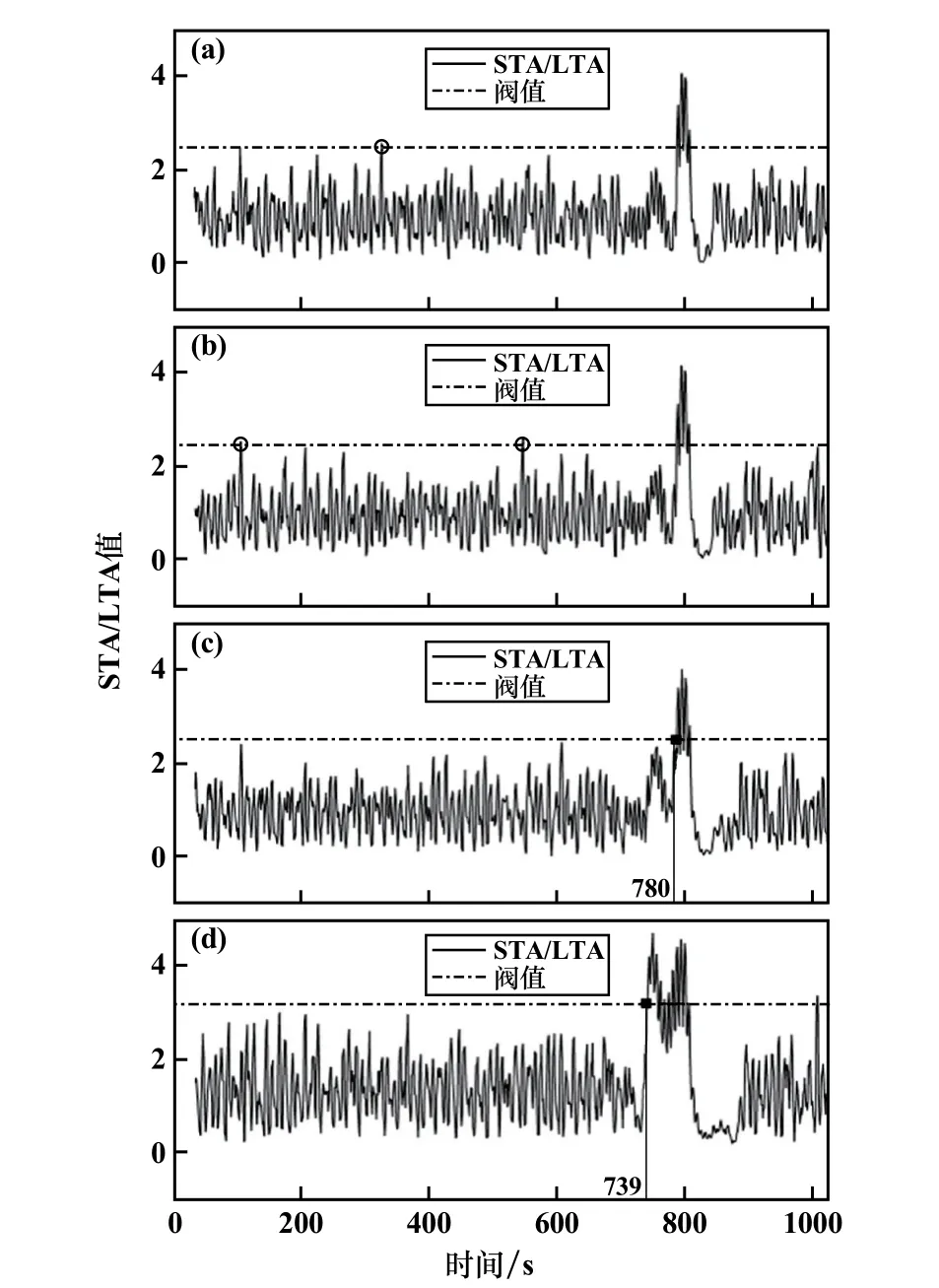
圖5 短時窗4 s時STA／LTA法到時拾取結果

3 礦山地壓監測系統實測信號到時拾取實例

為驗證本文方法在實際應用中的有效性，抽取廣西盤龍鉛鋅礦地壓監測系統實測的10組信號作為實例進行驗證，拾取結果如表2所示，表中“無”代表不存在聲發射。其中每組監測信號采樣數1 024個，采樣間隔為200μs。

表2 實測信號拾取結果表

對實測信號的拾取結果與人工法、STA／LTA法（短窗口取8×200μs、長窗口取32×200μs、閾值取2.5）拾取結果進行了對比，可以發現本文方法可以準確識別實測信號中有無聲發射信號，而STA／LTA法在對4、5、8號信號進行識別時出現了誤判。在準確度上，STA／LTA法對2、3、9號信號的拾取結果優于本文方法，但STA／LTA法對7、10號信號的拾取結果卻出現了較大偏差，在平均偏差上本文方法明顯比STA／LTA法小。由以上綜合分析可以發現，本文方法在實測信號上的拾取表現明顯優于STA／LTA法，且表現出較強的穩健性和適用性。

4 結 論

1）依據波形的起伏特征提出了一種新的到時拾取方法，該方法首先通過功率譜密度圖獲得信號包絡線的隱周期，然后通過STL分解法對信號包絡線進行去周期處理得到包絡線的趨勢變化曲線，最后通過MK突變檢測確定AE信號到達時間。

2）仿真實驗結果表明，在不同強度和不同頻率的噪音環境下，本文方法均表現出較強的穩健性，且準確率也明顯高于STA／LTA法。本文方法不需要事先設置參數，擺脫了傳統方法對參數設置的依賴性，具有更強的適應性。

3）在實測信號中應用后發現，本文方法能很好地識別監測信號有無AE信號，且與人工法拾取的結果相差較小。在實測信號應用中，本文方法表現性能明顯優于STA／LTA法，在礦山實測信號處理上具有較強的穩健性。