HPM視角下的雙曲線高三復習課教學研究

張佳淳 舒適 秦語真

【摘 要】研究者利用雙曲線的四種定義、旦德林雙球模型、標準方程推導方法、雙曲線的現實應用等史料，設計有內在邏輯關聯的數學問題串，復習了雙曲線定義、方程推導及性質應用等內容，實現了數學史的多元教育價值。

【關鍵詞】數學史;雙曲線;高三復習課

高三雙曲線復習課第一課時主要圍繞“雙曲線及其標準方程”“雙曲線的性質”等知識點進行系統梳理與知識鞏固。其中，“雙曲線的標準方程”與“雙曲線的性質”分別是滬教版高二數學下冊第12章第5節和第6節的內容。縱觀上海數學教科書的內容編排，雙曲線是繼橢圓之后的又一類圓錐曲線，是從曲線方程視角研究的重要二次曲線之一。

有鑒于此，筆者嘗試從HPM視角來設計雙曲線高三復習課的教學，旨在通過數學史問題的解決，復習雙曲線定義、方程推導及性質應用等內容，構建知識之諧，彰顯方法之美，實現能力之助，展示文化之魅。

一、歷史材料及其運用

（一）雙曲線的定義

（二）雙曲線第一定義的誕生

法國數學家拉希爾（P.de Lahire）在《圓錐曲線新基礎》一書中給出了雙曲線的第一定義，這是在有關文獻記載中首次出現第一定義。

1822年，比利時數學家旦德林（G.P.Dandelin）在一篇文章中利用圓錐的兩個內切球，在圓錐上推導出雙曲線的第一定義[6]，從而在古希臘阿波羅尼奧斯的截面定義和17世紀拉希爾的第一定義之間架起了一座橋梁。

（三）雙曲線標準方程的推導

歷史上，除了用今天人們耳熟能詳的兩次平方法推導雙曲線標準方程，數學家還采用了其他方法進行推導。

將（3）式代入（1）式或（2）式，即得雙曲線標準方程。

除了兩次平方法作為教科書中的方法需要復習鞏固，平方差法與第一定義聯系緊密，也可以通過設計問題加以落實。此外，和差術、余弦定理法也可以讓學生了解推導雙曲線標準方程的不同思路，從而拓寬學生思維，建立不同知識之間的聯系。

（四）雙曲線作圖法的出現

17世紀荷蘭數學家舒騰（F.van Schooten）在《幾何練習題》中設計了雙曲線的兩種作圖工具[10]，如圖2和圖3，這兩種工具均利用了雙曲線的第一定義。

教師讓學生思考舒騰的第一種雙曲線規為什么能畫出雙曲線的一支，既回顧了雙曲線的第一定義，又提高了學生的邏輯推理和直觀想象素養。

（五）雙曲線的現實應用

雙曲線的現實應用比較廣泛，主要有以下幾個方面。

（1）光學應用。從雙曲線一個焦點發出的光，經過雙曲線反射后，反射光線的反向延長線都匯聚到雙曲線的另一個焦點上[11]。因此，可以利用雙曲線的光學性質來制作望遠鏡。

（2）建筑學應用。雙曲線在圖形學上叫作貝塞爾曲線（Bezier curve），它是最有利于流體流動的一種曲線。熱電站、核電站的冷卻塔都采用雙曲線的結構，利用循環水自然通風冷卻，使得冷卻器中排出的熱水在其中冷卻后可重復使用[12]。

（3）軍事應用。雙曲線在通信定位上也有廣泛的應用，因為雙曲線上的點到兩個點的距離之差是定值，所以根據兩條雙曲線的交點可以確定位置。同時，雙曲線也被應用于雷達[13]和導航[14]中，如Loran（Long Range Navigation）系統。

二、教學設計與實施

（一）引入：雙曲線規與第一定義

上課伊始，教師介紹荷蘭數學家舒騰的生平及其在傳播笛卡兒解析幾何思想方面的貢獻，并通過改編舒騰雙曲線規的問題引入課題。

師：那PF-PC實際上就是什么？

生：就是GF或DC。

師：所以點P滿足雙曲線的第一定義，其軌跡為雙曲線的一支。下面我們一起來回顧雙曲線的第一定義。

在學生敘述雙曲線第一定義之后，教師讓學生辨析常數2a不小于F1F2，以及a=0時的動點軌跡，并通過以下練習題幫助學生鞏固第一定義。

（二）回望：歷史上的雙曲線定義

師：第一定義只是雙曲線概念發展過程中的一個片段。公元前3世紀，古希臘數學家阿波羅尼奧斯用一個平面去截一個圓錐面，當截面與圓錐面的母線不平行，也不通過圓錐頂點，且與對頂圓錐都相交時，截面與圓錐面的交線就是雙曲線，所以雙曲線也被稱為“來自立體的軌跡”。阿波羅尼奧斯的截線定義與我們教科書所采用的第一定義是否等價呢？請大家思考一下。

師：1679年法國數學家拉希爾首次明確提出雙曲線的第一定義，還有一種定義就是第二定義，請大家思考例2的問題。

生：拋物線。

生：用矩陣。

教師引導學生用兩次平方法推導焦點在x軸上的雙曲線的標準方程，并類比得到焦點在y軸上的標準方程。

（三）應用：雙曲線的價值

生：實軸長2a。

師：如果知道實軸長2a，兩個發射塔的距離2c，那么就可以確定雙曲線。然后再設一個副發射塔（教師標出圖4中點C），從副發射塔B與副發射塔C同時發射信號，根據點P處接收信號的時間差，再確定另一條雙曲線。最后通過兩條雙曲線的交點就可以把輪船的位置算出來。

接著教師講解冷卻塔與雙曲線的聲學和光學性質。

師：雙曲線有如此廣泛的應用，接下來我們要像費馬一樣更深入地研究雙曲線的性質。

（四）研究：旦德林雙球模型

教師引導學生通過代數方法，從雙曲線方程入手研究雙曲線的幾何性質，即對稱性、頂點、范圍、漸近線等性質。

生：這是偶函數。

師：是函數嗎？

生：不是，它關于y軸對稱。

師：如果關于y軸對稱，這需要用代數進行證明。

生：把（-x，y）代進方程。

師：如果它也關于x軸對稱，把什么代進去？

生：把（x，-y）代進方程。

師：如果它還關于原點對稱，把什么代進去？

生：把（-x，-y）代進方程。

師：所以雙曲線的性質不是從圖上看出來的，而是要用代數方法進行研究。因為當你研究一個陌生的方程時，你可能不知道它的圖形是什么樣的，所以要依靠方程去研究它的性質。

至此，學生已完成雙曲線基礎知識的復習，對第一定義也有了更扎實的理解。接著，教師出示例4，通過由旦德林雙球模型改編的問題揭示原始定義與第一定義的聯系。

師：你們覺得哪兩個點是焦點？

生：我感覺是點F1和F2。

師：那么我們就要證明點P到兩個點F1和F2的距離之差，即證明PF2-PF1是定值。那怎么證明？

學生陷入思考之中。

師：我們再來看看已有條件。兩個球與平面β相切，兩個切點是焦點，同時球又和圓錐內表面相切，怎么理解“球與圓錐相切”？

師：（教師用手比畫模型中位于下方的球）這個球和這個圓錐的什么線相切？

生：與母線相切。

師：與母線相切，這是非常關鍵的一點。因為點P在圓錐面上，所以這個點P肯定在某條母線上，母線一定穿過圓錐的頂點，因此點P和圓錐頂點確定一條直線，這條直線與下方的球切于點A，與上方的球切于點B。那PB就是上方這個球的切線，PF2也是球的切線，這兩條線段有什么關系呢？（教師畫草圖輔助演示）圓外一點如果引兩條切線，切線長相等，那么球外一點引同一個球的兩條切線呢？

生：也相等。

師：那么PF2等于什么？

生：PF2=PB。

師：同理，PF1是切線，PA也是球的切線，那么能得出什么結論？

生：PF1=PA。

師：所以PF2-PF1等于什么？

生：PB-PA。

師：PB-PA也等于什么？

生：AB。

師：AB是什么？

生：AB是上面的小圓錐母線長加下面的小圓錐的母線長，長度是定值。

師：這就是旦德林雙球模型，其實兩個球的半徑不一樣也是可以的。距今2300年前，古希臘數學家們用平面去切圓錐，得到了圓錐曲線。當我們理解了證明過程，就理解了旦德林雙球模型，從模型中導出了第一定義，在原始定義和第一定義之間架起了一座橋梁，也就知道了雙曲線的焦點是怎么來的。

接著，教師展示例5，旨在通過例5引出焦半徑公式與雙曲線標準方程的多種推導方法。

生：答案是15或3。

師：為什么？

生：由定義可以得出，一個答案是15，另一個答案是3。

師：這位同學考慮到定義中的絕對值，非常嚴謹。如果把題目中點P到焦點的距離改成2，答案又是多少？這時我們要審視一下雙曲線上的點到焦點的距離。雙曲線上的點到焦點的距離用什么公式呢？

學生陷入思考之中。

師：橢圓上的點到焦點的距離用什么公式？

生：焦半徑公式。

師：那么焦半徑公式又是如何得到的呢？

（教師通過板書，利用賴特的平方差法推導雙曲線焦半徑公式）

生：是8。

師：除了平方差法，還有洛必達法，但是后者技巧性非常強。

（五）小結：主題的升華

教師結合雙曲線的歷史和應用，出示以下文字作為課堂小結。

在漫長的一千多年時間里，古代數學家致力于用純幾何的方法研究圓錐曲線的性質。之后因為幾何問題不斷推廣，出現越來越多無法解決的復雜情況。直到笛卡兒發明平面直角坐標系，圓錐曲線的研究才步入一個新時代——從代數視角、解析方法研究幾何性質。希望同學們善于運用數學史中的方法解決問題，甚至提出問題，并不斷完善和創新。

三、結語

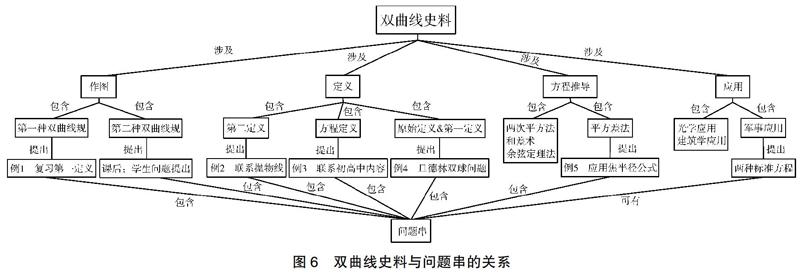
數學史融入高三課堂的落腳點是問題解決，因此教師可以從HPM視角設計有內在邏輯關聯的數學問題串。圖6呈現了雙曲線史料與本節課所用問題串之間的關系。

為了設計基于數學史的問題串，本節課采用了自由式、條件式、復制式、對稱式[15]等問題編制策略。首先，教師希望解決原始定義與第一定義之間的差距，但從學生心理序而言，并不適合在課堂伊始就展示旦德林球，因為學生不清楚為什么會出現旦德林球，所以教師先采用自由式策略，根據第一種雙曲線規的使用方法，自行設定條件和目標提出例題1，旨在復習鞏固第一定義。其次，教師認為在通過問題解決剖析四種定義后，再呈現旦德林雙球模型，才能使學生的學習水到渠成。所以教師采用條件式策略，改變雙曲線第二定義中離心率e的取值范圍，并且將方程定義中曲線方程的一般形式特殊化，從而改編得到例題2和例題3。接著，教師采用復制式策略，讓學生通過例題4經歷旦德林當年攻克原始定義與第一定義關聯的過程，讓學生看到數學家勤奮、刻苦的品質和數學演進發展的過程，傳遞數學人文性的一面。最后，為了說明焦半徑公式的應用，教師將推導雙曲線方程的條件與結論互換，利用對稱式策略提出已知方程求焦半徑的例題5，從而揭示焦半徑公式這一知識之源。另外，為了充分運用史料，教師還將第二種雙曲線規作為課后閱讀材料，要求學生根據史料提出數學問題，幫助學生在問題提出的過程中檢視自己的學習情況。

總而言之，本節雙曲線高三復習課從數學史出發設計一系列問題，同時按照教科書從定義到代數方程，再到利用解析幾何思想研究雙曲線性質及其應用的邏輯順序，將問題串聯成線，以溫故知新為目標，加深學生對雙曲線概念的理解;以問題解決為途徑，提升學生數學抽象、直觀想象、邏輯推理、數學運算等素養;以數學文化為抓手，鼓勵學生像舒騰、旦德林等數學家一樣善于思考、嚴謹求實，增強高三學生的自信心，滲透數學的科學價值、應用價值與文化價值，落實立德樹人根本任務。不過，本節課中，若執教者將軍事應用中的兩條雙曲線特殊化，使其焦點分別位于x軸和y軸上，再設計相關問題，則可實現數學史更豐富的教育價值。

參考文獻：

[1]YOUNG J W.Analytic geometry[M].Boston：Houghton mifflin company，1946.

[2]YOUNG J R.The elements of analytical geometry[M].Philadelphia：Carey，Lear & Blanchard，1835.

[3]WENTWORTH G A.Elements of analytic geometry[M].Boston：Ginn & company，1891.

[4]DAVIES C.Mathematical dictionary and cyclopedia of mathematical science[M].New York：A. S. Barnes & Co，1856.

[5]RUNKLE J D.Elements of plane analytic geometry[M].Boston：Ginn & Company，1888.

[6]SMITH E S.Analytic geometry[M].New York：John Wiley & Sons，1954.

[7]DE LHOSPITAL M.Traité Analytique des Sections Coniques[M].Paris：Montalant，1720.

[8]WRIGHT J M F.An algebraic system of conic sections & other curves[M].London：Black & Amstrong，1836.

[9]PEIRCE J M. A text-book of analytic geometry[M].Cambridge：J.Bartlett，1857.

[10]VAN SCHOOTEN F.Exercitationum mathematicarum[M].Lvgd Batav：Johannis Elsevirii，1657.

[11]CLAUDEL J.Handbook of mathematics for engineers and engineering students[M].New York：McGraw Publishing Company，1906.

[12]KALTENBORN H S.Meaningful Mathematics[M].New York：Prentice-Hall，1951.

[13]TAYLOR A E.Calculus，with Analytic Geometry[M].New Jersey：Prentice- Hall，1959.

[14]NATHAN D S.Analytic Geometry[M].New York：Prentice-Hall，1947.

[15]汪曉勤.基于數學史料的高中數學問題編制策略[J].數學通報，2020（5）：9-15.

（責任編輯：陸順演）