基于ARIMA 模型的區(qū)間道路短時車流量預(yù)測研究

楊東龍

（天津大學(xué)，天津 300072）

隨著機動車數(shù)量呈指數(shù)形式增長，尤其是在上下班高峰期及節(jié)假日時期，城市道路堵塞嚴(yán)重，增加了居民的出行成本，使道路交通面臨著巨大的壓力[1]。運用智能交通系統(tǒng)是緩解目前問題的有效措施，而精準(zhǔn)的實時車流量預(yù)測是發(fā)展智能交通的重要環(huán)節(jié)[2]。

根據(jù)時間維度的不同可以將車流量的預(yù)測劃分為長時（年）車流量預(yù)測、中時（月/日）車流量預(yù)測和短時（時/分）車流量預(yù)測[3-5]。長時及中時車流量數(shù)據(jù)的周期性較強、隨機干擾較弱，而短時車流量的數(shù)據(jù)具有高度不確定性，預(yù)測較為困難且精度不高[6]。目前，用于短時車流量預(yù)測的模型[7-8]大概分為兩類：一類是通過多影響因子進行車流量曲線的擬合，包括XGboost、GBDT、隨機森林等，該類模型依賴于影響因子的選取，在現(xiàn)實中難以完全獲取相應(yīng)數(shù)據(jù)；另一類是基于內(nèi)生變量本身進行預(yù)測，包括ARIMA、LSTM、KNN 等，該類模型數(shù)據(jù)獲取成本低，易于實現(xiàn)[9]。

文中基于ARIMA 算法[10-12]提出了一種改進型的短時車流量預(yù)測模型。ARIMA 算法只在下一個周期有較好的預(yù)測表現(xiàn)，該改進模型根據(jù)需要預(yù)測的時間周期個數(shù)，將短時車流量數(shù)據(jù)劃分為對應(yīng)的數(shù)據(jù)集組，每個數(shù)據(jù)集組預(yù)測下一個時間周期的車流量，從而實現(xiàn)多個時間周期的準(zhǔn)確預(yù)測。仿真實驗證明了該改進算法的普適性和準(zhǔn)確性。

1 ARIMA算法

短時車流量預(yù)測屬于時間序列預(yù)測[13-14]，這一類預(yù)測建模相對一般的回歸模型更加復(fù)雜，因為時間序列的數(shù)值是按照時間先后順序進行排列的，預(yù)測值依賴于時間次序。自回歸移動平均（ARIMA）算法是一種典型的時間序列預(yù)測算法。ARIMA 的基本原理是在時間序列平穩(wěn)化的過程中，對因變量的滯后值、產(chǎn)生隨機誤差的滯后值及當(dāng)前值進行預(yù)測。ARIMA 的五大核心概念為平穩(wěn)性、自回歸、移動平均、自回歸移動平均、差分。

1）平穩(wěn)性：指時間序列yt在n階以下的所有矩取值均與時間無關(guān)，ARIMA只適用于平穩(wěn)的時間序列。

2）自回歸（Autoregressive，AR）：指利用自生變量的歷史時間數(shù)據(jù)對未來時間數(shù)據(jù)進行預(yù)測。p階自回歸公式如下：

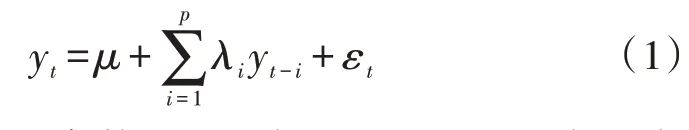
式中，μ表示常數(shù)項；εt表示誤差項；λi表示自相關(guān)系數(shù)。

3）移動平均（Moving Average，MA）：指通過自回歸模型中誤差項的累加實現(xiàn)預(yù)測中隨機波動的有效消除。q階移動平均的計算公式如下：

式中，μ表示常數(shù)項；εt表示誤差項；θi表示誤差項系數(shù)。

4）自回歸移動平均：即AR 與MA 的結(jié)合，表示為ARMA(p,q)，公式如下：

5）差分（Integrate，I）：指時間序列的當(dāng)前值減去滯后值，d階差分公式表示如下：

ARIMA 的建模流程如圖1 所示。其要求時間序列數(shù)據(jù)是平穩(wěn)的，若數(shù)據(jù)不平穩(wěn)，則需要進行差分。在確定了合適的d值以后，算法就轉(zhuǎn)化為求解平穩(wěn)時間序列Δdyt的問題，然后再將Δdyt構(gòu)建為ARMA(p,q)，加上差分次數(shù)即可表示為ARIMA(p,d,q)。其中，p表示自回歸階數(shù)；d表示差分次數(shù)；q表示移動平均階數(shù)。本質(zhì)上，ARIMA 先對擬合值進行線性相加，再通過自身變量進行預(yù)測。

圖書館服務(wù)理念要突破傳統(tǒng)圖書館在空間、時間、人員等方面的限制，為高校師生的教學(xué)科研服務(wù)、為師生的專業(yè)拓展服務(wù)。2015年7月，由美國新媒體聯(lián)盟編寫的，北京開放大學(xué)翻譯的《新媒體聯(lián)盟地平線報告（2015高等教育版）》指出：未來的幾年內(nèi)，正式學(xué)習(xí)和非正式學(xué)習(xí)融合，更多的移動學(xué)習(xí)和在線學(xué)習(xí)在高校廣泛應(yīng)用。現(xiàn)在已經(jīng)有很多人通過互聯(lián)網(wǎng)聽到、看到、感受到在線教育的便捷。它因為具有名校名師效應(yīng)、免費、高質(zhì)量的優(yōu)勢，成為當(dāng)下流行的課程選擇。筆者認(rèn)為，在線教育不僅僅是一種課程形式，它在本質(zhì)上是互聯(lián)網(wǎng)+知識的共享形態(tài)。圖書館在互聯(lián)網(wǎng)+時代的服務(wù)應(yīng)該與網(wǎng)絡(luò)資源結(jié)合，更好地為師生利用網(wǎng)絡(luò)提供高效、便捷的服務(wù)。

圖1 ARIMA算法流程圖

2 短時車流量預(yù)測模型

2.1 數(shù)據(jù)準(zhǔn)備

圖2 為區(qū)間道路3 天的車流量數(shù)據(jù)圖，數(shù)據(jù)時間間隔為15 min，該區(qū)間3 天總車流量共59 513 輛，平均每天19 838 輛。從圖中可以看出，每天6:00 之前區(qū)間道路車輛數(shù)量較少，每天8:00 和18:00 左右有1～2 小時的早晚高峰，且車流量較大。因此，選取第一天6:00 到第三天18:00 時間段的數(shù)據(jù)作為訓(xùn)練集，來預(yù)測下一個小時內(nèi)每隔15 min 的車流量。

圖2 短時車流量數(shù)據(jù)圖

2.2 平穩(wěn)性和非白噪聲檢驗

ARIMA算法只適用于平穩(wěn)的非白噪聲時間序列，因此需要對訓(xùn)練集進行平穩(wěn)性和非白噪聲檢驗[15-16]。

文中采用ADF 進行平穩(wěn)性檢驗（單位根檢驗）。當(dāng)判斷序列是否平穩(wěn)時，首先觀察第二部分顯著性p_value。若p_value 小于0.05，則證明單位根有解，即表示時間序列平穩(wěn)；若p_value 比0.05 大，則證明非平穩(wěn)；若p_value 接近于0.05，則要通過τ值與臨界值進行綜合判斷[17]。

穩(wěn)定性檢驗后再進行非白噪聲檢驗，并返回白噪聲檢驗結(jié)果標(biāo)志參數(shù)P值。若P值小于0.05，則表示在95%的置信水平區(qū)間拒絕原假設(shè)，證明時間序列為非白噪聲序列；否則，時間序列為純隨機序列，無法進行預(yù)測。

2.3 時間序列定階

為了確定ARIMA（p,d,q）模型中的p、q值，研究中采用自相關(guān)函數(shù)（ACF）和偏自相關(guān)函數(shù)（PACF）判斷模型階數(shù)法。求取訓(xùn)練集差分后平穩(wěn)序列的ACF 和PACF，如圖3 所示。

圖3 自相關(guān)和偏自相關(guān)圖

根據(jù)自相關(guān)和偏自相關(guān)圖，結(jié)合表1 確定訓(xùn)練集的ARIMA 模型p、q值分別為1、0。確定 后進行ARIMA 模型擬合預(yù)測，即可得到未來1 個小時內(nèi)每15 min 的預(yù)測值。

表1 ARIMA模型選擇方法表

3 改進型預(yù)測模型

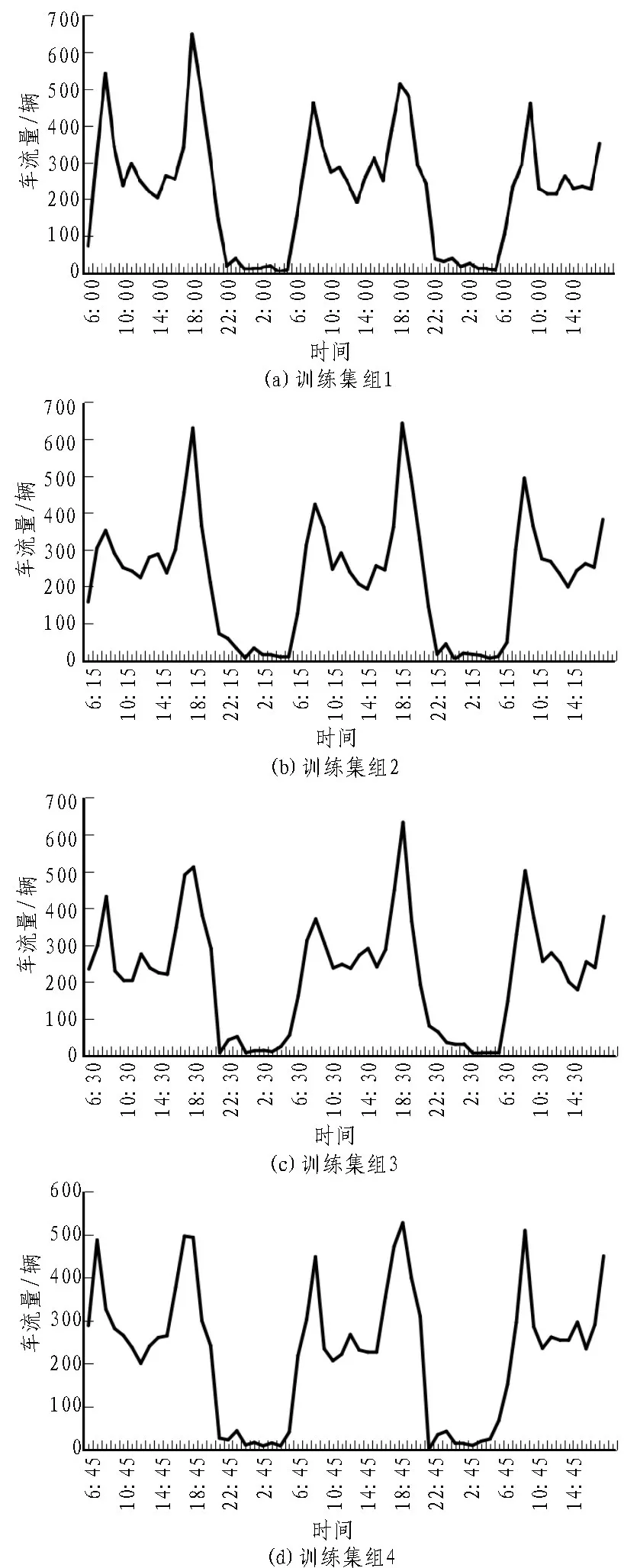
圖4 改進模型訓(xùn)練集組1～4

4 模型評估結(jié)果

4.1 評價指標(biāo)

構(gòu)建適合短時車流量預(yù)測模型，實質(zhì)上需要對不同模型的預(yù)測值和真實值通過量化的指標(biāo)進行評價，即評估不同模型預(yù)測值的準(zhǔn)確程度[19]。研究中選取了MAPE 與MAE 作為評價指標(biāo)。

MAPE，即平均絕對百分比誤差，其公式為：

式中，yi為真實值，為預(yù)測值，n為樣本量。MAPE的取值范圍為[0,+∞)，通常MAPE=0%表示完美模型，MAPE＞10%表示劣質(zhì)模型。

MAE 為平均絕對誤差，評估的是真實值和預(yù)測值的偏離程度，即預(yù)測誤差的實際大小。MAE 的值越小說明模型越優(yōu)，預(yù)測越準(zhǔn)確，表達式為：

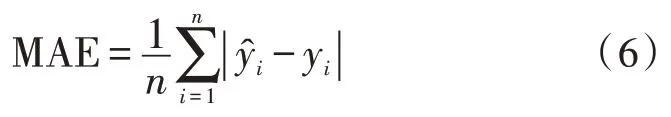
4.2 評價結(jié)果

采用經(jīng)典ARIMA 模型和基于ARIMA 的改進模型分別對短時車流量數(shù)據(jù)集進行訓(xùn)練，并對未來1個小時內(nèi)每15 min 的車流量進行預(yù)測。預(yù)測結(jié)果如圖5 所示。由圖5 可知，改進模型的預(yù)測效果明顯優(yōu)于經(jīng)典模型，改進模型的擬合程度更高。

圖5 不同模型預(yù)測結(jié)果

分別計算不同模型的MAPE 及MAE 值，如表2所示。經(jīng)典模型的MAPE 值為12.176 5%，MAE 值為73.212 6，屬于劣質(zhì)模型，對短時車流量的預(yù)測值不具有參考價值。改進模型的MAPE 值為4.019 6%，MAE 值為22.468 1，說明基于ARIMA 的改進模型在一定程度上對經(jīng)典模型進行了優(yōu)化。

表2 不同模型MAPE、MAE值

5 結(jié)束語

文中基于經(jīng)典的ARIMA 算法，針對其只在下一周期有良好預(yù)測表現(xiàn)的特點，通過劃分?jǐn)?shù)據(jù)集組的方式，使短時車流量曲線更加平滑，實現(xiàn)未來1 個小時內(nèi)每15 min 車流量的預(yù)測。仿真驗證了該改進模型的正確性與適用性，預(yù)測準(zhǔn)確率能夠達到95%以上，且改進模型無需依賴外部因子，調(diào)參方式簡單，可適用于任何場景的車流量預(yù)測。后期將對改進模型進行優(yōu)化，利用LSTM、Prophet 等時間序列預(yù)測算法的優(yōu)點與改進模型進行融合，進一步降低MAPE、MAE 值，提高預(yù)測的準(zhǔn)確率。