基于層次聚類和LSTM 的航空器到達時刻預測

翟俐民，張建偉，韓云祥

（1.四川大學視覺合成圖形圖像技術國防重點學科實驗室，成都 610065；2.四川大學計算機學院，成都 610065）

0 引言

近年來，隨著國民生活水平的提高和民航運輸業智能化的發展，空中交通流量急劇增加。根據2019 年民航行業發展統計公報[1]顯示，全行業完成旅客周轉量11705.30 億人公里，比上年增長9.3%，國內航線完成旅客周轉量8520.22 億人公里，比上年增長8.0%，全行業完成旅客運輸量65993.42 萬人次，比上年增長7.9%，國內航線完成旅客運輸量58567.99 萬人次，比上年增長6.9%。在航空器進港時終端區域空中交通嚴重擁擠的形勢下，航班延誤量逐年增加，不僅造成了極大的經濟損失，還對旅客的安全帶來一定的隱患。航空器接近終端區時，通過對航路點和到達時刻的精確預測，對航空器進行合理調度，可以有效提高空中交通運行效率和進一步提供安全保障。歐美各國在航空器進港時預計到達時刻預測方面的研究較國內更早、更成熟，歐洲單一天空計劃（SESAR）和2015 年歐洲ATM 總體規劃概述了到2050 年實現“歐洲航空界在可持續航空產品和服務方面居世界領先地位，并滿足歐盟公民和社會需求”的愿景，準確、可靠的空中交通軌跡預測模型（TBO）的開發是下一代國家航空運輸系統（NextGen）的主要目標，同時也包括終端區進港航空器預計到達時刻預測模型。

國內外學者在航空器預計到達時刻的研究中主要基于航空器性能參數與運動學模型以及數據挖掘與混合機器學習的研究方法。Hwang 等人[2]提出基于交互式多模型算法；張軍峰等人[3]提出一種狀態相關模態切換的混合估計算法（SDTHE）；湯新民等人[4]構造航空器狀態連續變化的混雜系統模型；馬光輝等人[5]利用動態時間規整與層次聚類方法對歷史雷達軌跡進行分析；Bai 等人[6]在預測航空器到達時間中通過設置單變量與多變量的對比實驗，實時更新預測結果，同時將結果作為輸入變量用于航空器間隔保持算法；Mueller 等人[7]構建基于性能的預測模型，通過模擬航空器在空域中的飛行軌跡，分析不同航行階段預測誤差的主要影響因素，包括飛機重量、推力等。上述研究主要以建立運動學模型為主，對歷史雷達數據和氣象信息等影響因素考慮較少。陳強等人[8]基于歷史雷達軌跡分析，通過RBF 神經網絡構建進場航空器進港時的高度、速度、進場飛行距離與進場飛行時間的映射關系，利用正交最小二乘算法設計基于RBF 神經網絡的進場飛行時間預測模型，在考慮航空器機型的情況下，將航空器飛行時間預測的均方根誤差控制在50s 以內；鄭志祥等人[9]通過分析航班信息、天氣信息以及空中交通信息，基于隨機森林算法構建航空器到達時刻預測模型；李陽等[10]通過建立支持向量機訓練集，使用LS-SVM 方法建立航空器進場過程中的位置、高度、進場飛行速度及所需時間之間關系，預測航空器進場飛行時間，將航空器進場飛行時間預測的均方根誤差控制在11s。以上研究僅考慮單一方法在ETA 預測上的應用，對航空器進港時到達時刻的影響因素考慮不夠全面，在預測時有機型等限制條件。本文基于歷史航跡數據進行分析，利用層次聚類算法對航跡進行分類，通過構建LSTM 網絡預測模型，實現終端區進港航空器到達時刻的精確預測。

1 層次聚類

1.1 概述

聚類算法在許多實際工程中應用廣泛，由于聚類規則的差異有不同的算法，包括基于層次的、基于密度的、基于劃分的、基于模型的和基于網格的算法等。各種算法之間沒有明確優劣之分，通常根據對聚類對象和聚類結果的要求不同，選擇合適的聚類算法。考慮到聚類結果的不確定性和對聚類對象的距離相似度定義，本文采用層次聚類算法。層次聚類算法中，凝聚層次聚類相對于分裂層次聚類使用更為廣泛。

1.2 原理

凝聚層次聚類中，首先以單條航跡作為一個初始航跡簇，計算所有航跡簇之間的相似度，逐步聚合與其相近的簇，直到某個聚類終止條件被滿足。

假設聚類航跡數據集T中的航跡條數為nt，則其距離矩陣大小為nt×nt。初始化聚類參數：聚類終止判定閾值Dstop，離群航跡簇判定閾值Ddrop。將每條航跡Ti作為一個初始航跡簇Ci，C為航跡簇聚類結果集合。

計算兩兩航跡簇之間的距離，得到初始距離矩陣D。其中，兩條航跡之間的距離使用動態時間規整（DTW）進行衡量，航跡簇之間的距離為簇中每條航跡與另一個簇中每條航跡之間距離求和后取平均得到。航跡點數據為三維位置信息，計算其歐氏距離為航跡點之間的相似度。

定義當前航跡簇Ci的最小航跡簇間距離為D{Ci,Cj}，航跡簇Cj為距離當前航跡簇距離最小的簇，每輪聚類過程將D{Ci,Cj} 相等的簇歸為新的航跡簇中，同時將大于Ddrop的簇歸為離群航跡簇。每輪聚類結束后，若C中任意航跡簇間距離D{Ci,Cj} 均大于Dstop，則聚類終止；否則，重新計算并更新距離矩陣，進入下一輪聚類過程。

聚類性能評價指標使用戴維森堡丁指數（DBI），計算的是任意兩個類的類內平均距離之和與兩聚類中心距離的比值，其計算公式為：

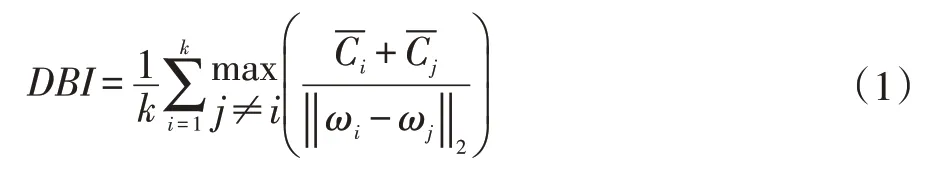
2 LSTM

長短期記憶網絡是一種循環神經網絡（RNN）。傳統的RNN 訓練困難，隱藏層只有一個狀態，對短期輸入非常敏感，在實際應用中很難處理長距離依賴，而LSTM 作為一種改進的RNN，成功地解決了傳統RNN的缺陷，通過增加狀態來保存長期輸入信息，從而更擅長處理時間序列問題，成為當下最流行的RNN 之一，在語音識別、自然語言處理等領域有眾多應用。

3 ETA預測模型

3.1 數據介紹

航空器預計到達時刻受多種因素影響，搜集了2019 年8 月到10 月成都雙流國際機場所有進港航班數據，其中包含：航跡點數據（經度、緯度、航向、高度、水平速度、垂直速度、到達時間等）、航空器基本信息（航班號、機型等）以及氣象數據（風速、風向等）。此外，還包括終端區空中交通流信息以及雙流機場終端區標準進場程序圖等。據分析，航跡點的采樣間隔約為15 秒，每天進港的航班數量大約有400 到500架次。

3.2 數據預處理

獲取到的航跡數據中，會出現航跡數據缺失、航跡點數目過于稀疏以及航跡點數據重復等現象，需要對初始航跡數據進行數據清洗。通過分析每條航跡的航跡點數目及其分布情況，將航跡數據缺失和航跡點較為稀疏的航跡排除，刪除重復航跡點數據，同時，對于航跡點數目相對較少的航跡，采用數據插值的方式進行數據增強。

將經緯度坐標數據，通過墨卡托投影變換將其轉換為以機場為坐標原點的二維平面坐標數據。利用墨卡托投影正解公式，將經緯度坐標(B,L)轉換為平面直角坐標系(X,Y)，標準緯度B0，標準經度L0，e為第一偏心率，e'為第二偏心率，a為長半軸長，b為短半軸長，坐標系轉換公式為：

將層次聚類結果作為航跡分類類別通過數值編碼添加到特征數據中。對于類別型特征數據（如機型），通過One-hot 編碼將其轉換為數值型數據。對數值型特征數據需要進行歸一化與標準化處理，以消除由于不同特征之間量綱不同帶來的負面影響。

歸一化函數式為：

標準化函數式為：

3.3 預測模型

基于層次聚類和LSTM 的航空器到達時刻預測步驟如下：

（1）選取訓練集、驗證集和測試集。將預處理后的航跡數據按照航跡條數進行隨機打亂，選取總樣本的80%作為訓練集以進行模型訓練，10%作為驗證集進行超參數調整和模型能力的初步評估，10%作為測試集來評估預測模型的泛化能力。

（2）判定航跡類別模型。對于訓練樣本，通過構建傳統分類模型對航跡進行分類，不同類別的航跡進港時位置、速度等信息差異較大，對預測模型的精確度有至關重要的影響。

（3）使用BP 神經網絡和LSTM 網絡進行對比實驗。BP 神經網絡使用Sequential 順序模型，包含輸入層、隱藏層和輸出層。LSTM 網絡由重復的鏈式神經網絡模塊組成，每個單元包含輸入門、遺忘門和輸出門。使用修正線性單元（Rectified Liner Unit）為激活函數，分別使用Adam 和SGD 為優化算法，以加快模型收斂速度。

（4）模型評價指標。實驗結果的評估主要使用兩個評價指標，分別為均方根誤差（RMSE）和平均絕對誤差（MAE），公式分別為：

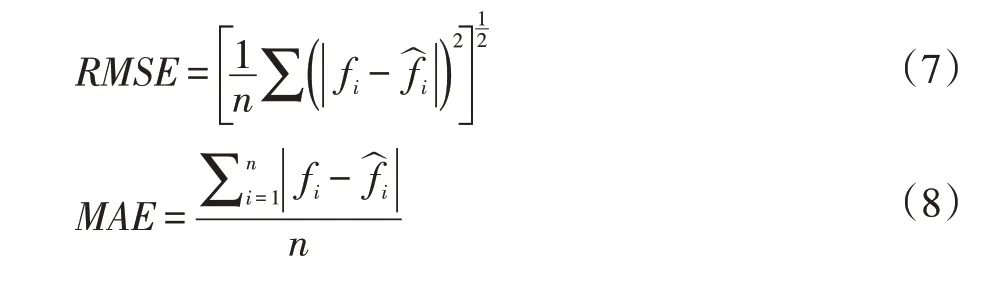
4 結果分析

航跡聚類結果不同、分類模型準確度以及ETA 預測模型參數不同對ETA 預測均有較大影響，將從以上幾方面對最終預測結果進行分析。

對航跡進行聚類時，由于在計算距離矩陣中使用的位置數據維度存在差異，聚類后的航跡簇類別個數也不同。使用經緯度二維信息進行聚類，聚類結果為6類。使用經緯度和高度三維信息進行聚類，聚類結果為8 類。相對于二維信息，增加高度維度使得航跡聚類時的分類效果更加精確，最終ETA 預測精確率提高了25%。

由于分類任務的復雜度較低，傳統的分類模型即可達到較好的效果，使用邏輯回歸和卷積神經網絡分別對航跡類別進行預測，其預測準確度分別為97.02%和98.22%。

對于LSTM 網絡，滑動窗口的大小對模型預測結果影響較大，當窗口較大時，預測ETA 所考慮的航跡信息越多，但窗口過大會導致過擬合現象，使得模型泛化能力降低。LSTM 網絡預測精確率相對于BP 神經網絡提高了18%，預測結果如表1。

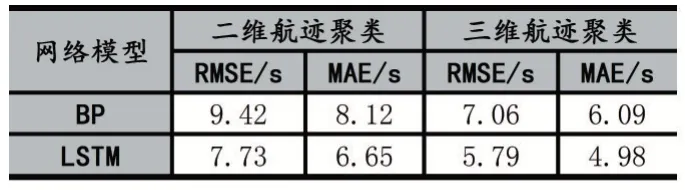
表1 預計到達時刻（ETA）誤差分析對比表

5 結語

本文從航跡點中的二維和三維位置數據出發，利用層次聚類算法建立二維航跡聚類模型和三維航跡聚類模型，通過構建邏輯回歸和卷積網絡傳統分類模型對航跡類別進行分類，同時考慮航跡點中的位置、航向、速度與航空器到達時刻之間的映射關系，利用BP神經網絡和LSTM 網絡建立預測模型。通過對比實驗發現可以將ETA 預測的均方根誤差控制在6s，具有較高的準確率。但在分析對航空器預計到達時刻的影響因素時，對于空域狀態的評估仍有不足，同時在聚類過程中出現的離群航跡未進行深入分析，后續將對此類問題做出進一步研究。